考虑季节差异性的不同时间尺度含风电系统旋转备用优化研究

温步瀛，卢鹏铭

(福州大学电气工程与自动化学院，福建福州350108)

考虑季节差异性的不同时间尺度含风电系统旋转备用优化研究

温步瀛，卢鹏铭

(福州大学电气工程与自动化学院，福建福州350108)

考虑风电出力和系统负荷的季节差异性较大，同时考虑风电出力预测误差和负荷预测误差随时间尺度的缩短而减小和电力系统旋转备用容量配置离不开机组组合的特点，本文建立考虑季节差异性下的不同时间尺度协调机组组合的含并网风电的电力系统旋转备用容量配置的模型。针对各个季节的风电出力和负荷变化特点，采用不同时间尺度协调机组组合的方法，对各个季节的场景进行分析，得出不同季节条件下的旋转备用优化方案。

风电并网;季节差异性;旋转备用;不同时间尺度

1 引言

风能具有随机性和难以预测性的特点。大规模风电的并网相当于向电力系统引入极大的不确定因素，这会严重影响系统的稳定性。为了保障系统安全可靠运行，就必须大幅度增加旋转备用容量［1-3］。

针对含风电的电力系统备用容量问题，学者们的观点主要有两种:一种是采用确定性方法来研究［4，5］，另一种则是采用随机变量来描述风电出力，将问题转换成求解不确定规划问题来解决［6］。但是采用这两种方法解决风电并网的不确定问题往往会使得系统旋转备用需求大量增加，降低了系统运行的经济性。电力系统的备用问题常常要与系统的机组组合相协调，且风电出力和负荷功率的预测误差水平具有随时间尺度减少而降低的特点，通过多次更新系统的风电出力预测信息可以减少风电并网带来的不确定因素［7］。风电出力和负荷预测具有季节差异性［8］，通过历史数据可以看出，不同季节的风电出力和负荷功率差异性非常明显，因此在预留旋转备用容量时应该针对不同季节的特点分别制定。

本文将考虑风电出力和负荷功率的季节差异性，基于不同时间尺度协调机组组合来研究含并网风电的电力系统旋转备用的优化配置问题。

2 含风电的电力系统旋转备用影响因素

2.1 发电机组的运行故障

发电机运行都存在一定的强迫停运率，一般可以采用二次型离散随机变量来描述。取qi为机组i的强迫停运率，对时段t的发电机组i生成在0～1之间均匀分布的伪随机数τi。令τi≤qi为机组i强迫停运，则机组启停状态ui.t置为0，否则ui.t置为1。

2.2 风电出力和负荷预测误差

对调度人员而言，相比于单纯的预测值，预测的不确定性分析更有指导意义。这主要表现在含风电的电力系统旋转备用容量的配置上。对大规模风电场群而言，当预测时间尺度较长时，风电出力的预测误差将趋向于正态分布［9］。同时风电出力的预测误差随着时间尺度的减少而减少。设风电出力预测误差为N(0，σ2w)，取系统负荷和风电出力之差为系统的实际负荷P'L。

受技术条件、自然和人为等因素的限制，负荷预测会有一定的误差。通常情况下认为负荷预测误差服从N(0，)的正态分布［10］。每个节点的预测误差不近相同，因此设第k个节点的负荷预测误差服从N(0，)的正态分布，一般情况下，节点间的预测结果是相互独立的，则总负荷预测误差服从N(0，)的分布，其中:

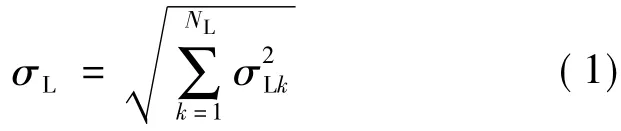
式中，NL为负荷节点个数;σLk为节点k的负荷预测误差;σL为总负荷预测误差。

由于风电出力预测和负荷功率的预测误差之间具有相互独立性，因此，总预测误差可以描述为服从N(0，)的正态分布，其中:

式中，σW、σD分别为风电出力和全网负荷功率的预测误差。

2.3 风电出力和负荷功率季节性差异

风能主要是由太阳辐射差异引起的气温和水蒸气含量不同而产生的地面气压差，气温在不同季节具有较大的差异性。通过历史数据可以看出，不同季节的风电出力和负荷差异特性非常明显，因此应该针对不同季节分别制定预留旋转备用的方案。图1、图2和图3分别是我国沿海某省在不同月份的风电出力、负荷功率曲线和各季度的典型日负荷曲线。

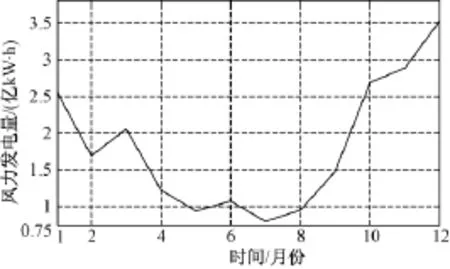
图1 某省全年各月的风力发电量Fig.1 Wind power electricity of each month throughout year

通过图1和图2可以看出，在不同月份的风力发电量和负荷需求量差异较大，风力发电量与负荷需求之间没有存在一定的关系，具有相对独立性。不同月份风电出力与负荷需求之间存在很大的差异性;而相同季节风电出力和负荷比例相似性较高。

在图3中可以看出日负荷的趋势基本保持不变，综合图1、图2和图3可以看出春秋季负荷和风电出力的相似度较高，对春秋季(第9～17周和第31～43周)可以采用同一个结果来优化。而夏季、冬季、春秋季风电出力和负荷之间的比例差别较大，则应该采用不同预留旋转备用容量控制策略。

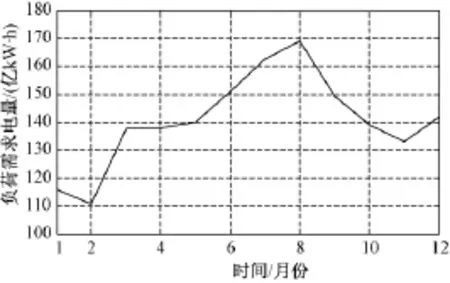
图2 某省全年各月的负荷需求电量Fig.2 Electricity load demand of each month throughout year

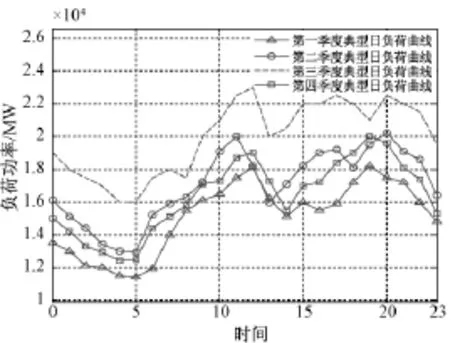
图3 某省各季度的典型日负荷曲线Fig.3 Typical daily load curves of each season

3 考虑季节差异性的不同时间尺度含风电的电力系统备用分配数学模型

3.1 不同时间尺度协调机组组合的旋转备用容量制定策略

风电出力预测和负荷预测的误差都具有一定的时效性，并随着预测时间步长的减少而减小。在不同季节负荷功率和风电出力具有较大的差异性，相同年份不同季节的负荷功率和风电出力差异性较大，不同年份相同季节的负荷功率和风电出力相似性较高，因此，可通过对每个季节进行典型分析，得出各个季节相应的优化旋转备用配置。目前，在时间尺度较大的风电出力预测上，日前风电出力预测可以为调度计划提供较有效的预测。一般情况下，大机组具有很高的启停成本，旋转备用容量的制定和分配又离不开机组组合。机组组合一般是在旋转备用容量和负荷预测功率的基础上制定，而旋转备用容量又受到机组组合的约束，通常通过机组组合结果所得的备用容量一般会大于或等于预留旋转备用容量。因此，协调机组组合的旋转备用优化主要是针对所需预留的旋转备用容量。

在不同时间尺度下，系统预留的旋转备用容量过低可能会引起调度计划的频繁修正，系统的经济性和可靠性都会受到影响;而预留过多的旋转备用容量会对系统的运行经济性造成影响。本文通过对比预留不同比例的最小旋转备用容量所需的系统运行费用，得到可以使含风电电力系统相对经济运行的旋转备用预留容量。而且由于不同季节风电出力和负荷功率特点差异性大，现将机组组合的制定策略分成三个时间尺度，通过协调各时间尺度机组组合，并针对各个季节风电出力和负荷功率特点，得到不同季节的旋转备用容量控制策略。

(1)以24h为时间尺度的日前调度计划

以24h为一个时间周期来制定所有机组的启停机方案主要根据日前机组的运行状态和负荷预测结果。由于日前风电出力预测和负荷预测的数据误差较大，在该时间尺度下预留旋转备用容量时可以适当降低供电可靠率的要求，从而提高系统运行的经济性。简称该时间尺度的调度计划为日前调度计划。

(2)以6h为时间尺度的短期修正调度计划

由于风电出力和负荷预测误差等不确定性因素随着距离执行时刻的缩短而减小，所以理论上通过时间尺度越短的方案来修正机组组合后的调度方案准确度越高，但是大部分机组的启停时间均需要4～6h，因此制定以6h为时间尺度来修正原来指定的以24h为时间尺度的机组组合和旋转备用计划，并简称该时间尺度的调度计划为短期修正调度计划。

(3)以1h为时间尺度的应急修正调度计划

尽管采用6h为时间尺度的预测数据已经有较高的精度，但是风能的随机性仍然较大，还有可能使得风电出力预测出现较大的偏离，这样原有的调度计划可能达不到实际精度的要求，而目前具有短时间启停功能的燃气机组的启停时间也需要1h。因此，以1h为时间尺度制定快速机组启停机方案来进一步保障系统的供电可靠性，并简称该时间尺度的调度计划为应急修正调度计划。

3.2 数学模型

(1)以24h为时间尺度的日前调度计划数学模型

日前调度计划以整个调度周期内的总发电成本最低为目标函数，同时，设风电和水电的短期发电运行成本为0，日前调度计划备用容量以一定比例的负荷预测值来制定。

目标函数为:

式中，Nt为日前调度计划划分的时段数;N0为常规机组的总数量;为当前日前调度计划所确定的机组i在时段t的启停状态;Fi为机组的运行成本;为当前日前调度计划所确定的机组i在时段t的出力状况;Si为机组i的启停成本;ai、bi、ci为机组i的经济特性参数。

约束条件:

1)系统功率平衡约束为:

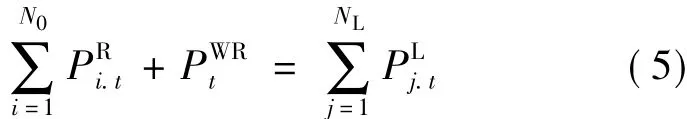
2)火电机组出力约束为:

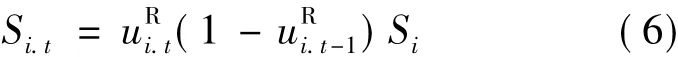
3)系统备用容量约束为:

4)火电机组最小运行和停机时间约束为:

(2)以6h为时间尺度的短时修正调度计划数学模型

短时修正调度计划备用容量的制定主要以满足系统的供电可靠率为目标来求取。一般情况下，系统不会出现两台或者两台以上发电机同时强迫停运，且系统等效负荷预测误差可视为服从正态分布。因此，在系统出现单台发电机组强迫停运和一定等效负荷预测误差时，系统的供电可靠性可以表示为［11］:

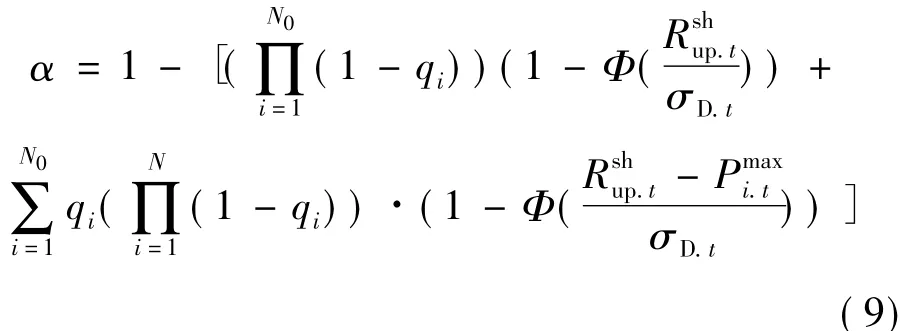
式中，α为系统的可靠性指标;Φ为正态分布函数; σD.t为时段t的等效负荷预测的均方根误差;qi为机组i的强迫停运率;为机组i在时段t时的出力上限;为时段t系统上调备用需求。

系统下调旋转备用可以表示为:

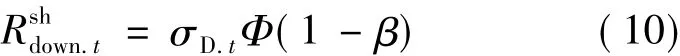
短时修正调度主要是通过启停中小火电机组来解决日前调度系统负荷功率或风电出力预测误差过大引起的系统可靠性指标不合格的问题，从而使系统可靠运行。

短时修正调度在更新的负荷和风电功率预测数据的基础上，以剩余时段的总发电成本最低为目标。目标函数为:

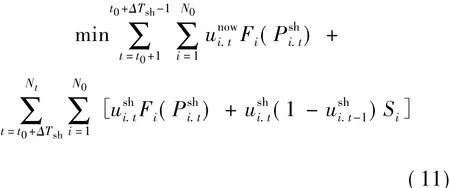
式中，t0为发现进行短时修正调度的时间点;ΔTsh为短时修正调度距机组实际执行的时间;为进行短时修正前的调度计划下机组在时段t的启停状态;为经过短时修正调度后机组在时段t的启停状态;为经过短时修正调度后机组在时段t的出力。

短时修正调度的其他约束条件和日前约束条件基本一致，但是参与启停的机组启停时间要小于6h。即:

式中，Tstart.i和Tstop.i分别为机组的启停时间。

(3)以1h为时间尺度的应急修正调度计划数学模型

水电是可再生能源，水电的出力理论上要全额上网，但是考虑到小型水电机组具有启停机速度快、启停费用较低的特点，应留有部分小型水电机组作为备用调节机组。应急修正调度计划主要是通过启停具有快速关停能力的燃气机组和容量较小的水电机组来解决由于风功率或者负荷发生大幅度突变引起的系统旋转备用无法满足可靠性要求的问题。

应急修正调度计划的目标是使得调整时段的发电总成本最低。目标函数为:

式中，t0为发现进行应急修正调度的时间点;ΔTyj为应急修正调度距机组实际执行的时间;为进行应急修正前的调度计划下机组在时段t的启停状态;为经过应急修正调度后机组在时段t的启停状态;为经过应急修正调度后机组在时段t的出力。

应急修正调度计划的约束条件和短期修正调度计划的约束条件基本一致。但是在应急调整计划中，只有具有快速启停能力的发电机组才可用于该调度计划的启停机状态调整。即:

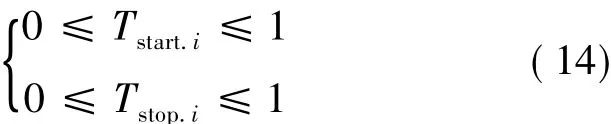
最后，冬季(第1～6周和第44～52周)、夏季(第18～30周)和春秋季(第9～17周和第31～43周)的典型日风电出力和负荷特性差别较大，而且水电、太阳能等电源出力季节差别性也很突出，旋转备用容量应针对各个季节的特点分别配置。因此，根据不同季节典型日负荷和风电出力的特点，分别采用不同时间尺度协调机组组合的方法来配置各个季节经济调度下所对应的旋转备用容量。

3.3 模型求解

该模型为滚动求取复杂约束的最优化模型，先采用优先顺序法求取各机组的启停机顺序，再通过粒子群算法(Particle Swarm Optimization，PSO)滚动计算来求解得出不同季节情景下相应备用容量水平所对应的系统调度计划的调整次数［12］、需要调整的时段、启停机费用和发电总费用等，从而得到各季节所对应的旋转备用的最优配置方案。

4 算例分析

本文采用由10个常规机组和50台2MW并网风力发电机组组成的电力系统，不考虑系统线路约束条件下，分成24个时段进行算例分析。各常规机组特性参数详见文献［13］，机组强迫停运率如表1所示。本算例中各季节的风电出力预测数据是基于实际风电出力数据，采用文献［14］的方法分成24h、6h和1h三种时间尺度分别对冬季、夏季和春秋季典型日风电机组的出力进行预测，所得结果分别如图4、图6和图8所示。本算例中各季节的负荷数据采用文献［15］的方法和误差预测精度，以RTS负荷数据(Reliability Test System Load Data)［16］中各季节的负荷功率特点为基础，分成24h、6h和1h三种时间尺度分别对冬季、夏季和春秋季典型日负荷进行预测，所得结果分别如图5、图7和图9所示。取系统的供电可靠性指标为0.95。

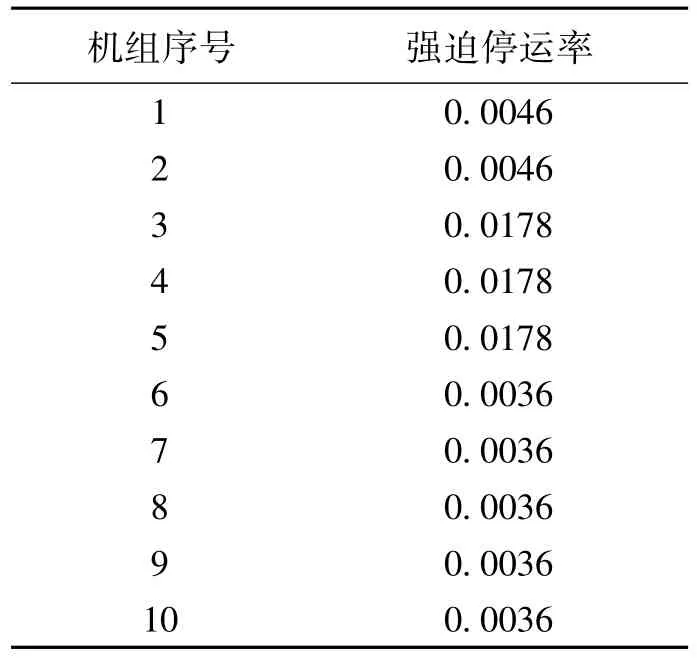
表1 机组特性参数Tab.1 Characteristic parameters of units

以不弃风和保障系统可靠运行为前提，对以上系统采用不同时间尺度协调机组组合方法，研究不同季节情景下含并网风电的系统备用容量的配置问题，并取24个时段中供电可靠性的最低值作为系统的供电可靠性水平，得出针对不同季节不同旋转备用水平下的最优调度情况，如表2所示。

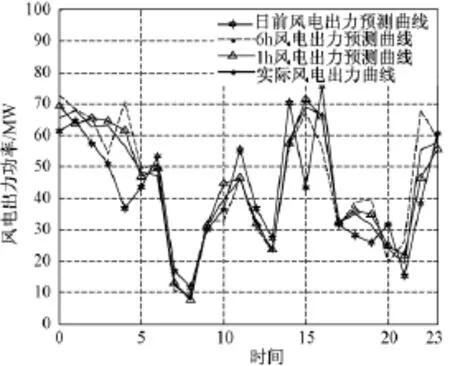
图4 各时段风电出力预测值和实际值(冬季)Fig.4 Data of wind power prediction and actual value(winter)

图5 各时段负荷功率预测值和实际值(冬季)Fig.5 Data of load forecasting and actual value(winter)

图6 各时段风电出力预测值和实际值(夏季)Fig.6 Data of wind power prediction and actual value(summer)

由表2可以看出，不同季节下所对应的不同时间尺度协调机组组合的旋转备用优化结果不同。在该算例中，采用不同时间尺度下协调机组组合来优化旋转备用方案，得出该系统冬季对应的最经济旋转备用比例是8%，而夏季和春秋季所对应的最经济旋转备用比例是5%和6%。这与该地区的风电出力具有“冬季多，夏季和春秋季少”的特点相符合。但是，夏季由于整体负荷功率较大，取得备用容量低可能引起调度计划调整次数的增加，而调整调度计划会产生一些额外的费用，设短时调度计划调整费用为2000美元/次，应急修正调度计划调整费用为3000美元/次。表3为考虑调度计划调整费用后的各季节对应的经济调度情况。

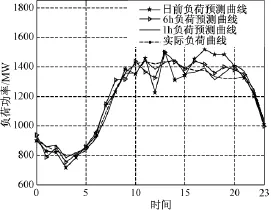
图7 各时段负荷功率预测值和实际值(夏季)Fig.7 Data of load forecasting and actual value(summer)

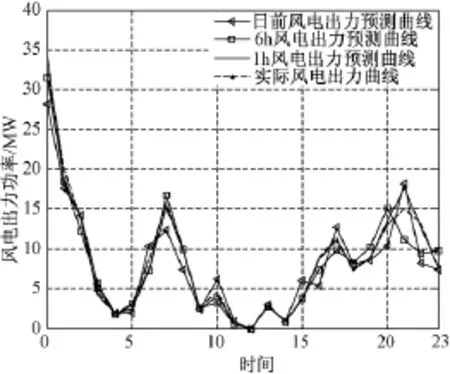
图8 各时段风电出力预测值和实际值(春秋季)Fig.8 Data of wind power prediction and actual value(spring and autumn)

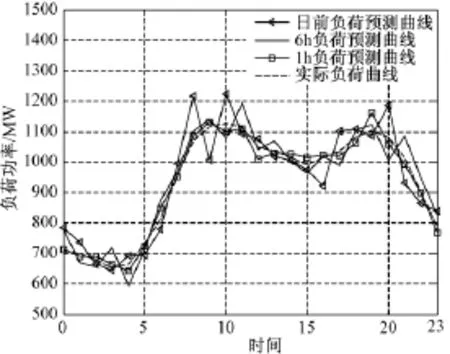
图9 各时段负荷功率预测值和实际值(春秋季)Fig.9 Data of load forecasting and actual value(spring and autumn)

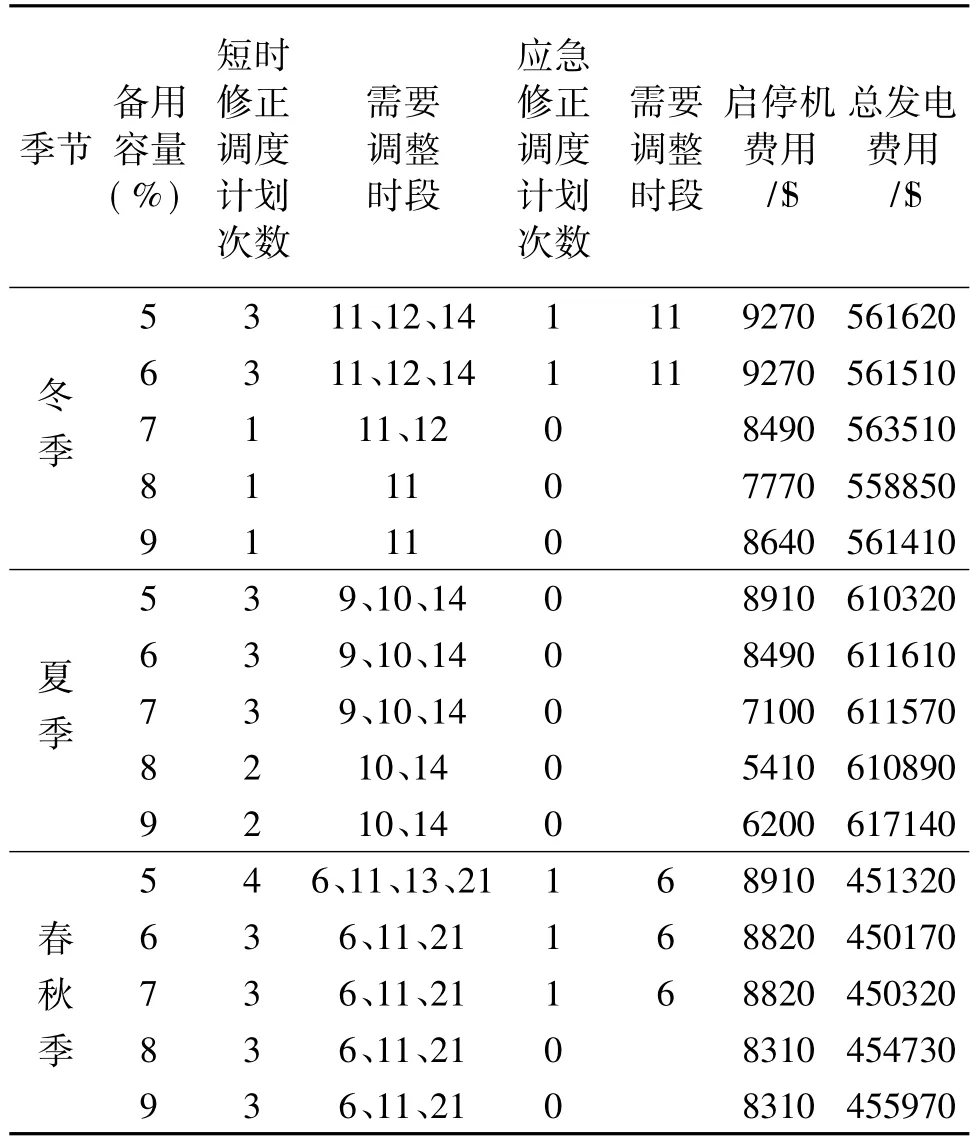
表2 不同旋转备用容量下的系统经济调度情况Tab.2 Economic dispatching under different spinning reserve capacities

表3 考虑调整调度计划费用后的系统经济调度情况Tab.3 Economic dispatch considering scheduling program adjustment costs

通过表3可以看出，考虑调度计划调整费用后，尽管该地区夏季的并网风电出力较小，但由于负荷容量大，旋转备用容量小会引起调度计划调整次数的增加，从而增加了调整调度计划的费用，考虑调度计划调整费用后，夏季的最经济备用容量为8%。

因此，考虑季节差异性，针对不同季节的典型日负荷和典型风电出力特点，采用不同时间尺度协调机组组合的方法来优化旋转备用可以使含并网风电的系统运行经济性得到进一步提高。

5 结论

针对风电出力和负荷功率的季节差异性较大，以及风电出力和负荷功率的预测误差随时间尺度的缩短而减少，同时考虑到旋转备用容量的配置离不开机组组合，本文通过考虑季节差异性，采用不同时间尺度协调机组组合的方法来实现旋转备用的优化配置。从算例定性定量分析的结果可以看出，不同季节对应的旋转调度优化结果具有一定的差异性。因此，针对不同季节的负荷和风电出力特性，分别采用不同时间尺度协调机组组合的方法来优化旋转备用容量的配置，可以进一步提高含并网风电系统运行的经济性。

［1］Soder L.Reserve margin planning in a wind-hydro-thermal power system［J］.IEEE Transactions on Power Systems，1993，8(2):1345-1354.

［2］Ortega-Vazquez M A，Kirschen D S.Estimating the spinning reserve requirements in systems with significant wind power generation penetration［J］.IEEE Transactions on Power Systems，2009，24(1):114-124.

［3］Dany G.Power reserve in interconnected systems with high wind power production［A］.Proceedings of IEEE Porto Power Tech Conference［C］.Porto，Portugal，2001.10-13.

［4］苏鹏，刘天琪，李兴源 (Su Peng，Liu Tianqi，Li Xingyuan).含风电的系统最优旋转备用的确定(Determination of optimal spinning reserve of power grid containing wind)［J］.电网技术 (Power System Technology)，2010，34(12):158-162.

［5］葛炬，王飞，张粒子(Ge Ju，Wang Fei，Zhang Lizi).含风电场电力系统旋转备用获取模型 (Spinning reserve model in the wind power integrated power system)［J］.电力系统自动化 (Automation of Electric Power Systems)，2010，34(6):32-36.

［6］王雁凌，许传龙，岳巍澎 (Wang Yanling，Xu Chuanlong，Yue Weipeng).时变可靠性约束下含风电系统旋转备用的随机规划模型 (A stochastic programming model for spinning reserve of power grid containing wind farms under constraint of time-varying reliability)［J］.电网技术 (Power System Technology)，2013，37(5): 1311-1316.

［7］张国强，张伯明，吴文传 (Zhang Guoqiang，Zhang Boming，Wu Wenchuan).考虑风电接入的协调滚动发电计划 (Optimization of operation reserve coordination considering wind power integration)［J］.电力系统自动化(Automation of Electric Power Systems)，2011，35 (19):18-22.

［8］于大洋，韩学山，梁军，等(Yu Dayang，Han Xueshan，Liang Jun，et al.).基于NASA地球观测数据库的区域风电功率波动特性分析 (Study on the profiling of China’s regional wind power fluctuation using GEOS-5 data assimilation system of national aeronautics and space administration of America)［J］.电力系统自动化(Automation of Electric Power Systems)，2011，35(5):77-81.

［9］王彩霞，鲁宗相(Wang Caixia，Lu Zongxiang).风电功率预测信息在日前机组组合中的应用 (Unit commitment based on wind power forecast)［J］.电力系统自动化(Automation of Electric Power Systems)，2011，35 (7):13-18.

［10］周双喜，王海超，陈寿孙 (Zhou Shuangxi，Wang Haichao，Chen Shousun).风力发电运行价值分析(Analysis on operation value of wind power resources)［J］.电网技术 (Power System Technology)，2006，30(14): 98-102.

［11］Venkatesh B，Peng Yu，Gooi H B，et al.Fuzzy MILP unit commitment incorporating wind generators［J］.IEEE Transactions on Power Systems，2008，23(4):1738-1746.

［12］江岳文，陈冲，温步瀛 (Jiang Yuewen，Chen Chong，Wen Buying).基于随机模拟粒子群算法的含风电场电力系统经济调度 (Economic dispatch based on particle swarm optimization of stochastic simulation in wind power integrated system)［J］.电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2007，26(3):37-41.

［13］Kazarlis S A，Baldrtzis A G，Petridis V.A genetic algorithm solution to the unit commitment problem［J］.IEEE Transactions on Power Systems，1996，11(1):83-92.

［14］王扬(Wang Yang).风电短期预测及其并网调度方法研究(Study on short-term forecasting and dispatching of wind power)［D］.杭州:浙江大学 (Hangzhou:Zhejiang University)，2011.

［15］谢源(Xie Yuan).负荷模型预测及其应用(Prediction of load model and its application)［D］.长沙:湖南大学(Changsha:Hunan University)，2013.

［16］C Grigg，P Wong，P Albrecht，et al.The IEEE reliability test system-1996［J］.IEEE Transactions on Power Systems，1999，14(3):1010-1020.

Spinning reserve optimization of power system with grid connected wind power at different time scales considering seasonal difference

WEN Bu-ying，LU Peng-ming
(College of Electrical Engineering and Automation，Fuzhou University，Fuzhou 350108，China)

In view of the large seasonal difference of wind power output and load demand，and also the smaller errors in prediction of wind power and load forecast at shorter time period，the paper establishes a mathematical model for the power system with grid connected wind power and with consideration of seasonal difference and spinning reserve capacity for different time periods.In light of seasonal difference in wind power output and load demand，the paper analyses the spinning reserve optimization scheme in different seasons by using the method of power system spinning reserve configuration.

wind power grid connection;seasonal difference;spinning reserve;different time scales

TM 732

:A

:1003-3076(2015)07-0045-08

2014-09-15

福建省自然科学基金资助项目(2013J01176)

温步瀛(1967-)，男，福建籍，教授，博士，研究方向为电力系统优化运行、电力市场和风电并网运行;卢鹏铭(1989-)，男，福建籍，硕士研究生，研究方向为电力系统优化运行。