电感储能型脉冲电源系统的半解析参数分析

丁健民，于歆杰，李 臻

(电力系统及发电设备控制和仿真国家重点实验室，清华大学电机系，北京100084)

电感储能型脉冲电源系统的半解析参数分析

丁健民，于歆杰，李 臻

(电力系统及发电设备控制和仿真国家重点实验室，清华大学电机系，北京100084)

针对电感储能型脉冲电源这一复杂动态系统的性能分析，提出了理论推导辅以数值计算的半解析参数分析法。以STRETCH meat grinder拓扑为例，选取了系统设计和运行阶段的二项关键参数，即充电截止电流I0和电感比nL。分时段采用拉氏变换和数值求解，得到电源系统各支路电流和电压。以此可便捷地获得八项系统性能指标，即充电时间T0、充电效率η、一次/二次电流倍增比m1/m2、换流电容最大储能百分比ηC、主管耐压Vsopm、电枢出射速度正比项∝v和电感内阻总能损ER。讨论了电源系统运行阶段I0对性能指标影响的单参数分析问题和设计阶段I0和nL对性能指标影响的多参数分析问题。该方法可方便地用图形方式呈现出复杂动态系统某性能指标随任一项或多项系统参数的变化趋势，快速发现元件和控制参数对性能指标的影响及灵敏度，以选定合适的参数。

电感储能型脉冲电源;半解析法;性能指标;参数分析

1 引言

为满足高机动作战需求，电源小型化成为电磁炮技术应用中的关键问题［1］。由于电感储能较传统的电容储能其储能密度高出一个数量级，近年来成为研究热点。在电感储能型电源充放电换路过程中，需要关断大电感电流，由此对关断开关和关断电路这两方面提出了新的问题。因此目前相关研究主要着眼于提出新型或改进拓扑，以及实现更高能级的实验装置。

当前，电感储能型脉冲电源的研究尚处于起步阶段，缺乏对拓扑进一步的理论方法支撑和系统参数分析，多为定性说明，辅以电路仿真和实验验证。

美国IAT(Institute for Advanced Technology)实验室对 meat grinder基本拓扑进行改进，提出了STRETCH(Slow Transfer of Energy Through Capacitive Hybrid)meat grinder拓扑，给出了换流电容电压峰值的表达式［2］。以2MJ炮口动能的电池-电感电磁发射系统为例，讨论了系统效率和尺寸受电池和电感参数的影响［3］。该项研究属于宏观概念性分析，而非定量分析。

清华大学于歆杰课题组提出了两项指标用于对三种电感储能型脉冲电源拓扑性能进行对比［4］，讨论了STRETCH meat grinder三项性能指标的表达式及其受两项系统参数的影响［5］。由于该研究只限于讨论特定系统参数对有限项的性能指标的影响，具有一定的局限性，用于参数分析的灵活性和普适性不足。

2 系统关键参数和性能指标的选取

2.1 设计参数与运行参数

STRETCH meat grinder是电感储能型脉冲电源的典型拓扑，如图1所示，主管Sop一般采用IGCT。关于STRETCH meat grinder电路的基本原理，在相关文献［2，4］中均有详细分析，在此不再赘述。

根据半导体器件开合引起的电路工作状态变换，可将拓扑的工作过程划分为五个时段，如图2所示。

(1)充电时段:初级电源Us给L1和L2充电至指定值I0。

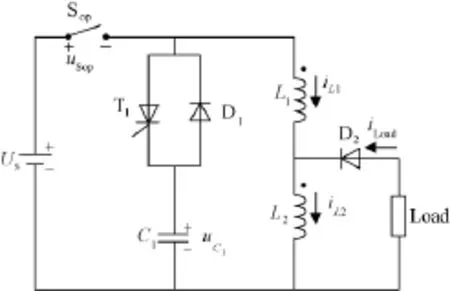
图1 STRETCH meat grinder拓扑Fig.1 Topology of STRETCH meat grinder

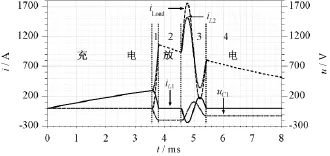
图2 电流/电压波形图和工作时段划分Fig.2 Current/voltage waves and working stage division

(2)放电第1时段:利用磁通压缩原理实现电流倍增，iL1降为0，iL2和iLoad达到一次峰值 IP1，uC1取得反向峰值UC1m。

(3)放电第2时段:仅L2向负载放电，uC1保持为UC1m不变。

(4)放电第3时段:从放电第1时段开始计时，延迟tD(大于放电第1时段时长)时间后，T1触发，C1释放放电第1时段中存储的L1漏感能量，以调整负载电流波形(该过程中iLoad取得二次峰值IP2)，直至iL1再次降为0。

(5)放电第4时段:仅L2向负载放电，uC1保持为恒定负值UC1end不变。

在拓扑结构确定后，待选定的系统参数包括元件参数(如L1、L2、C1等)和控制参数(如I0、tD等)。在电源系统设计阶段，指定系统能级，也即电感初始储能E0，待选定的元件参数和控制参数称为设计参数;在电源系统运行阶段，元件参数已经确定，待选定的控制参数称为运行参数。

本文中，将重点关注两项系统参数:①与系统能级、损耗和效率等密切相关的控制参数——充电截止电流(放电时段电感电流初值)I0;②主要影响磁通压缩、电流倍增的元件参数——电感比nL(=L1/ L2)。其中nL为设计参数，I0既为设计参数，也为运行参数。

2.2 性能指标

为量化参数对系统性能的影响，选取如下若干性能指标:

(1)充电时间T0:电感L1和L2从电流为0起，被电源Us充电至指定值I0的用时。

(2)充电效率η:电感初始储能E0与初级电源供能Es之比。

(3)一次电流倍增比m1:一次峰值(放电第1时段结束时负载电流)IP1与I0之比。

(4)二次电流倍增比m2:二次峰值(放电第3时段中负载电流峰值)IP2与I0之比。

(5)储能百分比ηC:换流电容C1在系统工作过程中的最大储能与电感初始储能E0之比。

(6)主管耐压VSopm:主管Sop承受的最大电压。

(7)电枢出射速度正比项∝v:因电磁发射电动力大小正比于，且放电时间一般为3～4ms，因此取自放电起3.5ms内积分，可大致正比于电枢出射速度。本文中，以小阻感负载替代实际轨道炮负载。虽然本项指标不能准确表示电枢出射速度，但其数值与出射速度存在正比关系。

(8)电感内阻总能损ER:充放电过程中两电感(L1和L2)各自的内阻RL1、RL2引起的总损耗。

3 半解析参数分析法

3.1 利用半解析法进行参数分析

因含多个储能元件，且涉及多个换路过程，直接求解STRETCH meat grinder电源系统的八项性能指标的解析表达式以开展参数分析是相对困难的。因此，本文提出一种半解析法，即在复频域基于拉氏运算电路分时段进行理论推导，辅以基于Mathworks Matlab®的数值求解，得到电源系统各支路电流、电压的全时域曲线，再由此计算获得2.2节所述八项性能指标数据。

在该半解析法基础上，通过扫描一项或多项系统参数，即可得到不同(组)系统参数下的性能指标数据，由此可方便地用图形方式呈现某项性能指标与一项或多项系统参数的函数关系，从而快速分析任一项或多项系统参数对性能指标的影响及其灵敏度，并选定合适的元件和控制参数使综合性能有最佳表现，达成参数分析和优化的目标。

与利用电路仿真软件、手工反复调整参数以开展研究的方式相比，本文提出的方法能够同时考虑多项参数对性能的综合影响，且具有计算速度上的绝对优势。由于待分析讨论的参数和性能指标的选取是自由的，且该半解析法也可推广至XRAM［6］等其他拓扑的研究，因此用于电感储能型脉冲电源系统的参数分析，具有较好的灵活性、普适性和可推广性。

3.2 基于拉氏运算电路和数值计算的半解析法

以下讨论中，初级电源采用电容Cs(考虑内阻Rs)表达，预充电压为U0，负载用小阻感LL与RL的串联近似，L1和L2间的互感为M。

充电时段的拉氏运算电路如图3所示。图中，我们将储能电感L1和L2作为整体考虑，Ltot=L1+ L2+2M，Rtot=RL1+RL2。

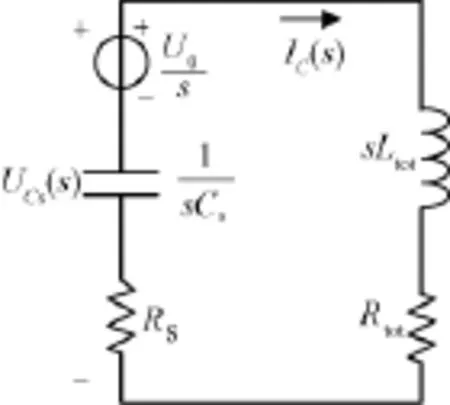
图3 充电时段拉氏运算电路Fig.3 Laplace arithmetic circuit of charging stage

根据图3所示电路，容易得到方程:

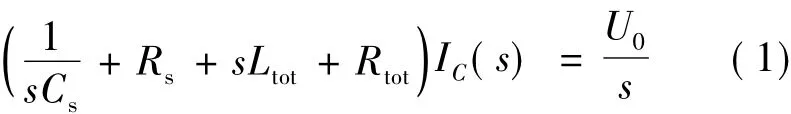
由式(1)求得IC(s)，利用Matlab函数impulse ()得到时域iC(t)，当iC达到指定值I0时，该时段结束。

放电第1时段的拉氏运算电路如图4(a)所示，图中将互感效应以流控电压源的方式体现。

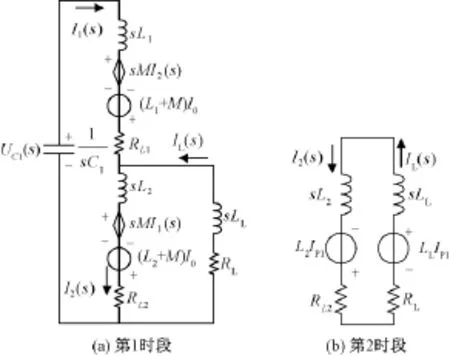
图4 放电第1、第2时段拉氏运算电路Fig.4 Laplace arithmetic circuit of discharging stages 1 and 2

对图4(a)中两网孔分别列写回路方程并联立:

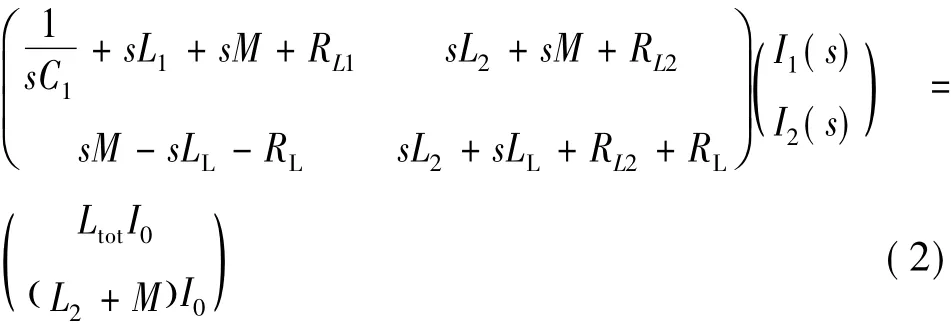
由式(2)可求得I1(s)和I2(s)，且有UC1(s)=－I1(s)/(sC1)，得到时域iL1(t)、iL2(t)、iLoad(t)(= iL2(t)－iL1(t))和uC1(t)，当iL1降为0时，该时段结束。此时iL2和iLoad为一次峰值IP1，为下一时段初值，uC1为UC1m。

放电第2时段的拉氏运算电路如图4(b)所示。根据图4(b)所示电路，容易得到方程:

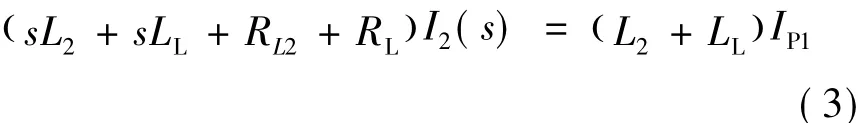
由式(3)得到I2(s)，进而得到iL2(t)和iLoad(t) (=iL2(t))。当该时段与放电第1时段用时之和达到tD时，该时段结束。此时iL2和iLoad为I30，为下一时段初值。该时段iL1保持为0，uC1保持为UC1m。

放电第3时段拉氏运算电路如图5(a)所示，对互感效应采用类似图4(a)的处理方法。

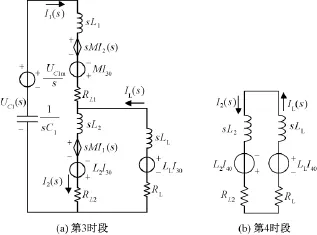
图5 放电第3、第4时段拉氏运算电路Fig.5 Laplace arithmetic circuit of discharging stages 3 and 4

对图5(a)中两网孔分别列写回路方程并联立:

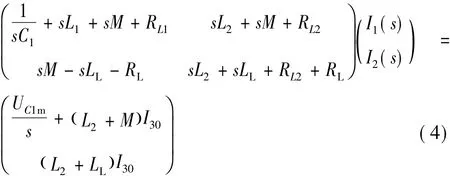
由式(4)求得I1(s)和 I2(s)，且有 UC1(s)= UC1m/s－I1(s)/(sC1)，得到时域iL1(t)、iL2(t)、iLoad(t)和uC1(t)。当iL1经过二阶振荡再次降为零时，该时段结束。此时 iL2和 iLoad为 I40，为下一时段初值，uC1为UC1end。

放电第4时段的拉氏运算电路如图5(b)所示。根据图5(b)所示电路，容易得到方程:

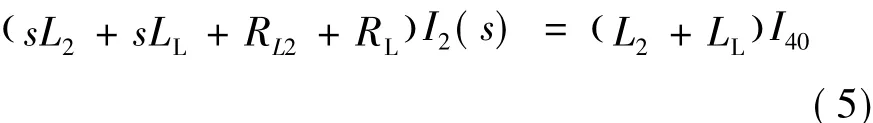
由式(5)得到 I2(s)，进而得到 iL2(t)和 iLoad(t)，足够时长(3～5倍时间常数)后，结束该时段计算。该时段iL1保持为0，uC1保持为UC1end。

衔接充电时段和放电第1～4时段，即得电感电流iL1、iL2、负载电流iLoad和换流电容电压uC1的全时域曲线，并由此计算得到八项性能指标数据。

3.3 半解析法的正确性验证

基于高性能系统仿真软件Ansoft Simplorer®对电感储能型脉冲电源进行仿真，已证实仿真结果与实际试验结果通常具有较高的吻合度［7］。因此，采用与电路仿真结果进行对比的方法，来校验3.2节半解析法所得性能指标数据的正确性。

仿真原理图如图6所示(略去控制信号)，元件参数已在图中标注，控制参数为:U0=200V，I0= 1kA，tD=1.2ms，仿真步长取0.1μs/1μs。半解析法下的电源系统参数设置与此一致。该电源系统Ltot=886.7μH，E0=443J。两种方法各自计算得到的性能指标及相对误差如表1所示。

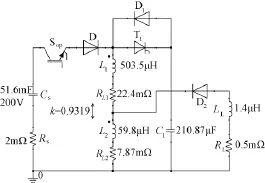
图6 Simplorer仿真原理图Fig.6 Simulation schematic based on Simplorer

由于3.2节理论推导中将半导体器件视为“理想”开关，未考虑其工作特性和开关损耗，所以半解析法所得放电时段的电流水平偏高。受此影响，含电流平方积分项的∝v和ER相较于仿真值的误差是最显著的。但总体而言，半解析法所得性能指标与仿真吻合较好，所以3.2节所述半解析法应用于电感储能型脉冲电源这一复杂动态系统的研究是可行的。

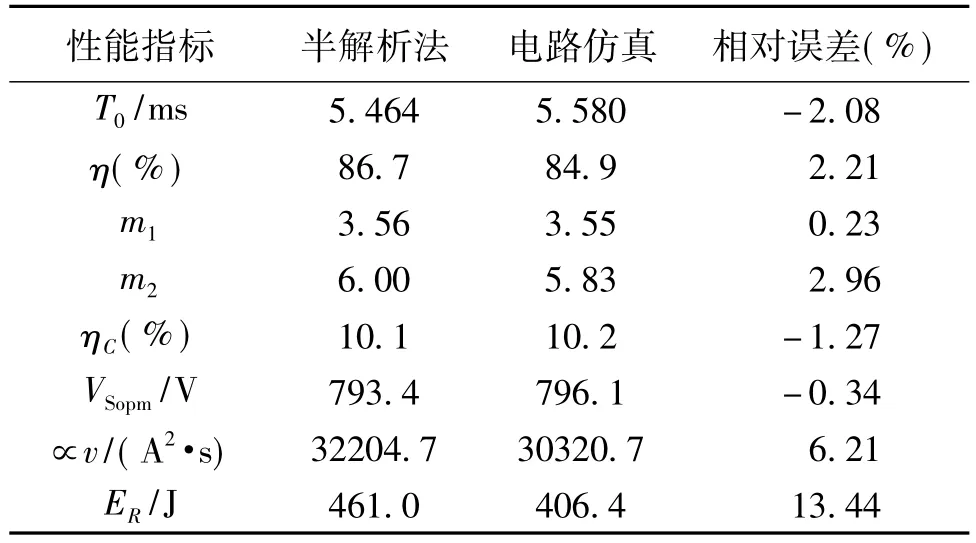
表1 半解析法和电路仿真所得性能指标对比Tab.1 Results comparison of performance indices between semi-analytical method and circuit simulation

4 电源系统设计/运行参数分析

利用半解析法可具体分析电源系统设计阶段I0和nL对性能指标影响的多参数分析问题，和运行阶段I0对性能指标影响的单参数分析问题。根据问题难易，先讨论后者。

4.1 运行参数I0对性能指标的影响

电源系统运行阶段，元件参数和除I0外的控制参数是确定的。对运行参数I0进行扫描，以3.2节所述方法获得不同I0下的性能指标数据，由此可绘制各性能指标随运行参数I0的变化图像。

以图6所示系统参数的拓扑为例，I0以步长50A由100A向1kA变动时，主管耐压VSopm的变化图像如图7所示。随着I0增大，VSopm几乎呈线性增大，表明I0的增大对VSopm表现为消极影响。

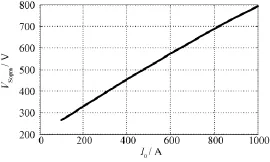
图7 主管耐压VSopm随运行参数I0的变化Fig.7 Variation of VSopmwith operation parameter I0

同理可分析I0的增大对其他项性能指标各自的影响，汇总结果见表2。

结果表明，m1、m2和ηC与运行参数I0无关，余下的五项指标中除∝v外，均随 I0的增大而恶化。因此，在使∝v足够大以满足出射速度要求的前提下，电源系统不宜在偏高的I0水平下运行。

表2 性能指标受运行参数I0的影响Tab.2 Influences of operation parameter I0on indices

4.2 设计参数I0和nL对性能指标的影响

电源系统设计阶段，系统能级E0是指定的，除储能电感参数外的元件参数和除I0外的控制参数均给定。电感参数中耦合系数k是确定值(或视为基本不变)。感值项L1和L2可由设计参数I0和nL唯一确定，如式(6)～式(8)所示。L1和L2确定后，内阻项RL1和RL2可由文献［8］给出的电感参数优化程序计算得到。

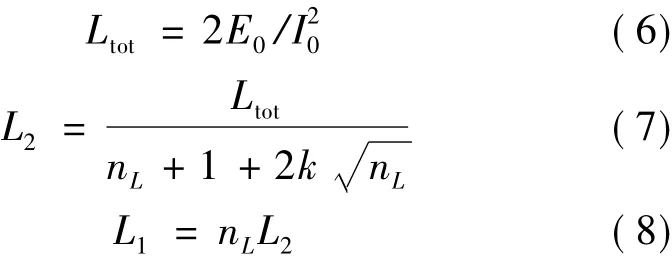
至此，所有系统参数都已给定或可由I0和nL确定。在外循环中扫描设计参数I0，对每一I0，在内循环中扫描设计参数nL，以3.2节所述方法获得不同组［I0，nL］下的性能指标数据，由此可绘制各性能指标随设计参数I0和nL的变化图像。

例如，系统能级E0指定为134J(图6所示拓扑I0取550A时的E0)，除储能电感外的元件参数、除I0外的控制参数及k值参照图6所示。I0以步长50A由100A向1kA变动，nL依次取4∶1、9∶1、16∶1、25∶1，二次电流倍增比m2的变化图像如图8所示。随着I0增大，m2略有降低;而随着nL增大，m2显著增大。这表明I0和nL的增大对m2的影响不一致，存在博弈。由于参数nL对性能指标m2的灵敏度更高，因此总体上m2是增大的，即I0和nL的增大对m2表现为积极影响。

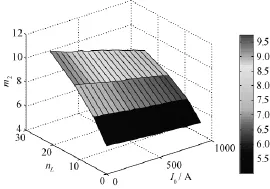
图8 二次电流倍增比m2随设计参数I0、nL的变化Fig.8 Variation of m2with design parameters I0and nL

同理可分析I0和nL的增大对其他项性能指标各自的影响，汇总结果见表3。

表3 性能指标受设计参数I0和nL的影响Tab.3 Influences of design parameters I0and nLon indices

结果表明，I0和nL对ηC和∝v等指标的影响具有一致性，对m1等指标的影响不一致，存在博弈，博弈的结果取决于两参数各自变化的程度和对相应性能指标影响的灵敏度。在设计阶段，可从主要关注的性能指标项出发来选定合适的I0和nL。

5 结论

本文提出了理论推导辅以数值计算的半解析参数分析法，以STRETCH meat grinder拓扑为例，系统地研究了电源系统参数对性能指标的影响。该方法在选取待分析的参数和指标上具有灵活性，且可推广到其他拓扑，相较于电路仿真方式在处理多参数问题和计算速度方面具有优势，较好地适用于电感储能型脉冲电源系统的参数分析。

I0和nL是设计/运行阶段的关键参数，二者的变化对性能指标的利弊影响不尽相同，在设计和运行阶段，根据主要关注的指标项来选定合适的I0和nL。

［1］李军，严萍，袁伟群 (Li Jun，Yan Ping，Yuan Weiqun).电磁轨道炮发射技术的发展与现状(Electromagnetic gun technology and its development)［J］.高电压技术(High Voltage Engineering)，2014，40(4): 1052-1064.

［2］Sitzman A，Surls D，Mallick J.Stretch meat grinder:a novel circuit topology for reducing opening switch voltage stress［A］.13th IEEE Pulsed Power Conference［C］.Monterey，USA，2005.493-496.

(，cont.on p.80)(，cont.from p.15)

［3］Dierks E，McNab I R，Mallick J A，et al.Battery-inductor parametric system analysis for electromagnetic guns［J］.IEEE Transactions on Plasma Science，2011，39 (1):268-274.

［4］初祥祥，于歆杰，刘秀成 (Chu Xiangxiang，Yu Xinjie，Liu Xiucheng).三种电感储能型脉冲电源电气性能的比较 (Electrical performance comparison of three inductive pulse power sources)［J］.电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2012，31(3):20-24.

［5］Shangang Ma，Xinjie Yu，Zhen Li.Determining key parameters for the STRETCH meat grinder circuit［A］.17th IEEE International Symposium on Electromagnetic Launch Technology［C］.La Jolla，USA，2014.1-6.

［6］Ford R D，Hudson R D，Klug R T.Novel hybrid XRAM current multiplier［J］.IEEE Transactions on Magnetics，1993，29(1):949-953.

［7］Xinjie Yu，Shangang Ma，Zhen Li.System implementation and testing of STRETCH meat grinder with ICCOS［A］.17th IEEE International Symposium on Electromagnetic Launch Technology［C］.La Jolla，USA，2014.1-6.

［8］Zhen Li，Xinjie Yu，Shangang Ma.Structural parameters optimization for the inductors used in the inductive pulse power supply［A］.17th IEEE International Symposium on Electromagnetic Launch Technology［C］.La Jolla，USA，2014.1-6.

Semi-analytical analysis on system parameters of inductive pulsed power supply

DING Jian-min，YU Xin-jie，LI Zhen
(State Key Laboratory of Control and Simulation of Power System and Generation Equipments，Department of Electrical Engineering，Tsinghua University，Beijing 100084，China)

For performance analysis of inductive pulsed power supplies，a method of semi-analytical parametric analysis based on theoretical derivation combined with numerical computation is proposed.Taking the STRETCH meat grinder circuit as an example，this paper has selected two key parameters during stage of system design and operation，i.e.charging cut-off current I0and inductance ratio nL.Current and voltage of any branch can be calculated based on time-slicing Laplace transformation and numerical calculation.Thus eight performance indices，i.e.charging time T0，charging efficiency η，primary/secondary current multiplication ratio m1/m2，ratio of the maximum capacitive energy over the total inductive energy ηC，the maximum voltage across the main switch Vsopm，muzzle velocity proportional term∝v，total energy loss caused by the inductors’internal resistances ER，can be easily obtained.The influences of the operation parameter I0and the design parameter I0and nLon the indices are particularly discussed.The change trend of any concerned index with one or more arbitrary parameters can be drawn in a diagram easily by using this method，thus the influences and sensitivities of component and control parameters on performance indices can be discovered quickly in order to select suitable parameters.

inductive pulsed power supply;semi-analytical method;performance indices;parametric analysis

TM91

:A

:1003-3076(2015)07-0011-05

2015-03-24

国家自然科学基金(51377087)、清华大学自主科研计划(20121087927)资助项目

丁健民(1990-)，男，回族，宁夏籍，硕士研究生，研究方向为脉冲功率技术;于歆杰(1973-)，男，贵州籍，副教授，博士生导师，博士，研究方向为无线电能传输、脉冲功率技术。