仿生粒子群算法在电力系统无功优化中的应用

王秀云，李 超，赵 宇，陈亚潇

(1.东北电力大学电气工程学院，吉林省吉林市132012;2.山东聊城供电公司，山东聊城252000)

仿生粒子群算法在电力系统无功优化中的应用

王秀云1，李 超1，赵 宇2，陈亚潇2

(1.东北电力大学电气工程学院，吉林省吉林市132012;2.山东聊城供电公司，山东聊城252000)

本文在标准粒子群算法的基础上，遵循群体寻优的生物特性，提出了仿生粒子群算法。初期将群体动态地分成多个子群，每个子群相对独立地向一个目标进化，子群的成员随着进化过程不断地更迭。后期增加子群间的信息交流，使算法更快收敛。该算法不仅丰富了种群的多样性，避免过早收敛于局部最优解，而且有较快的收敛速度。文中将该算法应用于电力系统无功优化中并与标准粒子群算法进行了比较，通过对IEEE30节点和IEEE118节点的算例仿真，证明了该算法的可行性和有效性。

电力系统;无功优化;仿生;分组;粒子群优化

1 引言

电力系统无功优化属于非线性规划问题，具有非线性、多约束、离散变量和连续变量相混合的特点［1，2］。解决这个问题的传统方法有线性规划法、内点法［3］和牛顿法等。近年来，针对传统算法在无功优化问题中的不足，学者们提出了启发式的智能算法，如遗传算法［4，5］、禁忌搜索算法［6］、差分进化算法［7］和粒子群算法(Particle Sward Optimization，PSO)［8-12］等，得到了较好的效果。

粒子群算法是Kennedy和Eberhant于1995年提出的一种多点搜索算法，具有易于实现、优化效率高和收敛速度快的优点［13］。但传统粒子群算法受当前最优位置的影响，容易陷入局部最优，导致收敛精度不高。为了克服这些缺点，本文提出了仿生粒子群算法(Bionic PSO，BPSO)。算法借鉴生物群体移动时，个体根据相对距离选择贴己的小伙伴的方法，自行分组并在组内寻优。当小组成员趋于稳定后，组间进行信息交流并寻找到共同的全局最优解。在运算的后期加入组间信息交流机制，使算法的收敛速度更快。最后将本文的算法在IEEE30和IEEE118节点系统上进行仿真验算。

2 无功优化的数学模型

电力系统的无功优化是指在满足约束条件的前提下，通过适当的方法(控制发电机端电压、改变无功补偿设备的无功出力和调节可调变压器的分接头等)改善电网中的无功功率流动，达到提高电压水平、减少有功网损的目的［14］。本文从系统的经济性出发，将有功网损最小作为评价标准，有功网损的表达式为:

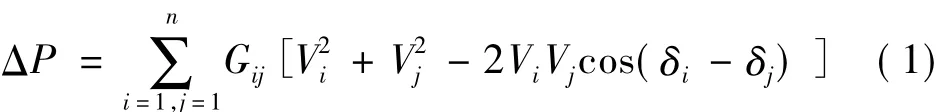
式中，ΔP为有功损耗;i、j为节点号;n为系统节点数;Gij为支路电导;Vi、Vj为节点电压的幅值;δi、δj为节点电压的相角。

等约束条件为:

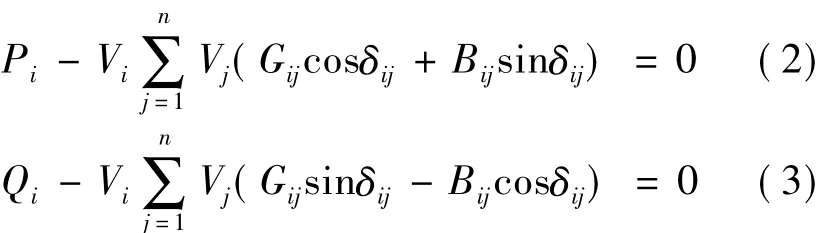
不等约束条件为:

式中，VGimax、VGimin分别为发电机i的电压幅值的上下限;Timax、Timin分别为变压器i的变比的上下限; Qcimax、Qcimin分别为补偿装置i的补偿量的上下限; VLimax、VLimin分别为负荷i的电压幅值的上下限; QGimax、QGimin分别为发电机i的无功出力的上下限。

考虑到负荷节点电压和发电机无功功率的越限问题，将这两个状态变量的越限行为以罚函数的方式处理，得到的目标函数为:

式中，FQ为目标函数;NG、NC和NPQ分别为发电机节点数、无功补偿节点数和PQ节点数;Qi为i节点发出的无功功率;λ1(t)、λ2(t)分别为电压越限和无功出力越限的惩罚因子，随着迭代次数的增加而线性递增;Vilim、Qilim分别为i节点电压和无功的限值，其定义为:

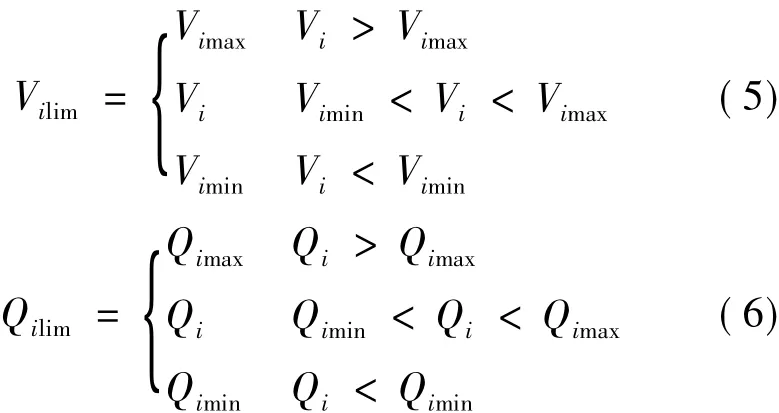
式中，Vimax、Vimin分别为i节点电压的上下限;Qimax、Qimin分别为i节点发出的无功功率的上下限。

3 标准PSO算法

粒子群算法来源于对简单社会模型的模拟，每个群体中的粒子在寻找最优解的过程中，需要考虑三个部分的因素:第一个部分是粒子当前速度的继承，是对自身状态的信任;第二部分是粒子自身的思考，是对亲身经历的总结;第三部分是粒子向同伴的学习，是粒子间的相互合作［15］。标准粒子群算法通过式(7)和式(8)来表达粒子的寻优过程:

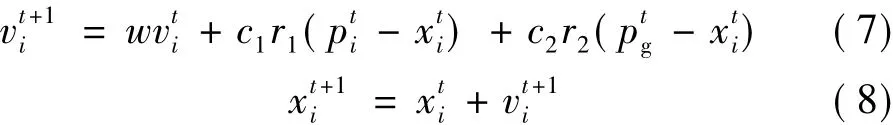
式中，t为迭代的次数;w为惯性权重，用来调节粒子对当前速度继承的多少;r1、r2为均匀分布在(0，1)之间的随机数;c1、c2为学习因子，通常取c1=c2= 2;、分别为第i个粒子第t次迭代时的位置和速度;为粒子的最优位置;为全局的最优位置。

4 仿生粒子群(BPSO)算法

4.1 分组方式

BPSO算法的分组依据是粒子间的相对距离，本文取空间中的两个多维向量的欧几里得距离作为粒子间的距离，公式为:

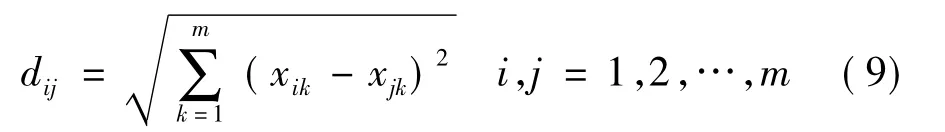
式中，dij为粒子i和j之间的距离;m为粒子的维数。

本文对粒子给出了距离极值r，称之为粒子的视野半径。当其他粒子j与粒子i的相对距离小于视野半径r时，则认为粒子j在粒子i的视野内，是粒子i的同伴，在粒子i之后的学习过程中起一定的作用。同理，有n个粒子，就有n个子群，但n个子群中会有对同一个子群的重复描述，即实际的子群数可能小于n。每个子群选择自己的成员并相对独立地进化，随着迭代的进行，粒子势必会向最优解聚集，逐渐靠近并进入彼此的视野，最终得到一个共识的最优解。

为了进一步丰富种群多样性和契合生物的特性，本文将每次迭代后所有粒子间距离的平均值作为视野半径r，在粒子逐渐聚集的过程中，r会随之变小。公式为:

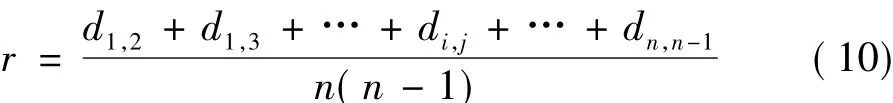
式中，di，j为粒子i和粒子j之间的距离，i≠j;n为粒子的总数。

因为每次迭代粒子移动的步长有一定随机性，而视野半径选取的是所有粒子间距离的平均值，所以小组成员是动态变化的，即旧成员可能会离开，成为别的子群的新成员，而不是简单的递增或不变。当视野半径r设为无穷大时，BPSO算法就变成了标准粒子群算法。

BPSO算法进化过程的公式表达为:

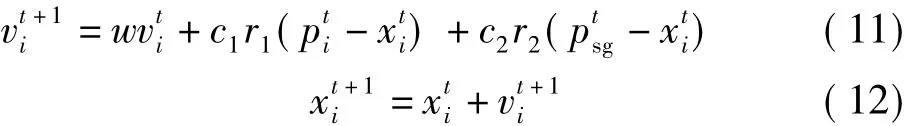
以上的想法符合生物群体移动的规律，粒子在群体中以独立的姿态存在，通过观察和学习视野内的同伴(距离大于视野半径r则无法相互交流)来调整自己速度的大小和方向。开始时群体稀疏，个体有开阔的视野，视野半径较大;后期群体聚集，个体被同伴包围，视野半径逐渐收缩。子群成员的随机变动也符合生物的偶然性。

4.2 群体经验的交流

为了提高BPSO后期的收敛速度，以一定概率的方式将落后的子群体的子全局最优替换成当前领先的子群体的子全局最优，增进子群体间的交流，使粒子群快速收敛于一个共同的最优解。实现的方法如式(13)所示:

粒子运动过程的示意图如图1所示，它更加直观地表达了上述方法的搜索过程。第一阶段是粒子初始状态，零散地分布在多维空间内，距离上有天然的远近;第二阶段是经BPSO算法分组后，各组独立进化、组内聚集的阶段;第三阶段是群体经验交流的阶段，各个子群逐渐融合成一个大的群体，寻找到共识的全局最优解。

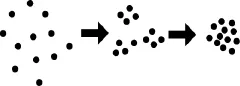
图1 粒子运动示意图Fig.1 Schematic of particle motion

4.3 算法流程

算法的流程如图2所示。

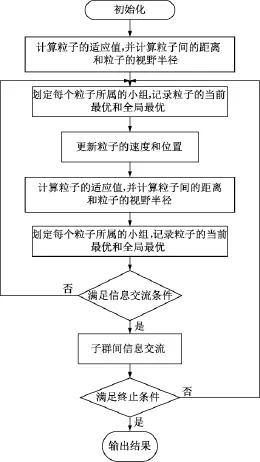
图2 BPSO无功优化流程图Fig.2 Flow chart of BPSO algorithm

5 算例分析

5.1 IEEE30节点算例

本文采用IEEE30节点系统验证BPSO算法的可行性和有效性。系统共有30个节点、41条支路。其中发电机母线编号为1、2、5、8、11、13，母线1作为平衡节点;可调变压器支路是(6，9)、(6，10)、(4，12)、(28，27);母线10和24装有无功补偿装置。其中发电机端电压为连续变化、变压器变比的步长为0.025pu、补偿电容器的调节步长分别为0.1pu和0.02pu。系统总负荷 PLoad=2.834pu、QLoad= 1.262pu，系统参数参见文献［16］。

初始条件下设发电机端电压和变压器变比均为1pu，节点电压上下限值为1.1pu和0.95pu。将标准PSO算法和BPSO算法程序种群规模选为50，分别运行30次，最大迭代次数为100次。PSO算法的惯性权重 w初始值取0.9，并按照 w(t)=0.9－(0.9－0.4)t/tmax线性递减，其中t是迭代次数，tmax是最大迭代次数，c1=c2=2.0。

发电机的端电压和无功出力的上下限结果见表1;优化后的各控制变量的结果见表2，其中V为发电机端电压，T为变压器分接头位置，Q为无功补偿器数据。将表2中优化后的控制变量取值与其限值比较，可以看出所有控制变量均在要求范围内，且有一定的裕度。

表1 30节点发电机无功出力及电压上下限Tab.1 Generator’s reactive power and voltage limits of IEEE 30 nodes

表2 优化后的控制变量Tab.2 Optimization status of control variables

两种算法各运行30次后，对这30次的结果进行数据分析，结果见表3。从表中可以看出，本文的BPSO算法优化后的最大、最小和平均网损均比PSO算法小。PSO算法优化后的平均网损是0.0281pu，BPSO算法优化后的平均网损是0.0278pu，降低了1.07%，说明该方法有效地降低了系统的网损。PSO算法运行 30次的结果大多零散地分布在0.0281pu周围，而BPSO算法30次几乎全部收敛于0.0278pu，从方差的大小同样可以看出，BPSO算法的收敛结果更加稳定。这说明BPSO算法在遇到局部最优时，可以有效地跳出来继续搜索，拥有更好的全局搜索能力。

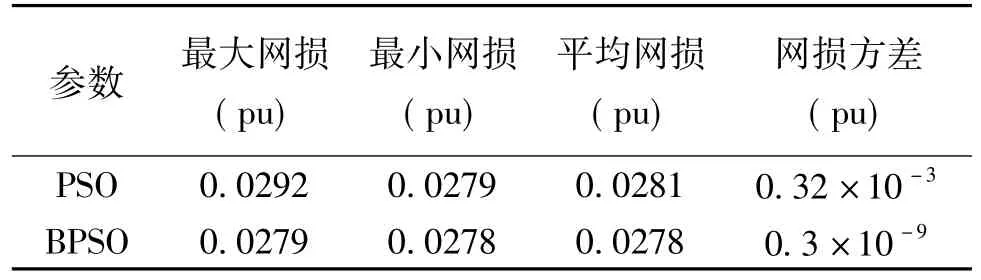
表3 无功优化结果(IEEE30)Tab.3 Reactive power optimization result(IEEE30)

图3为IEEE30节点系统标准PSO和BPSO算法的平均网损的收敛曲线。从图中可以直观地看出BPSO算法的平均网损明显小于PSO算法。而且两种算法在遇到相同情况时，PSO算法陷入了局部最优而BPSO算法会跳出来继续搜索，找到更好的优化方式减小网损。经30次统计，BPSO算法的平均收敛时间是15s左右，PSO算法是10s左右，BPSO算法的收敛速度比PSO算法稍慢，但若实际工程中采用高性能的计算机或者未来随着计算机运算能力不断提升，BPSO算法收敛时间上的劣势可以被忽略。

图3 IEEE30节点平均网损收敛曲线Fig.3 Convergence curves of average active power loss for IEEE 30 bus system

5.2 IEEE118节点算例

在算法参数和种群规模不变的前提下，采用IEEE118节点系统进行无功优化，优化后标准PSO算法和BPSO算法的结果见表4。

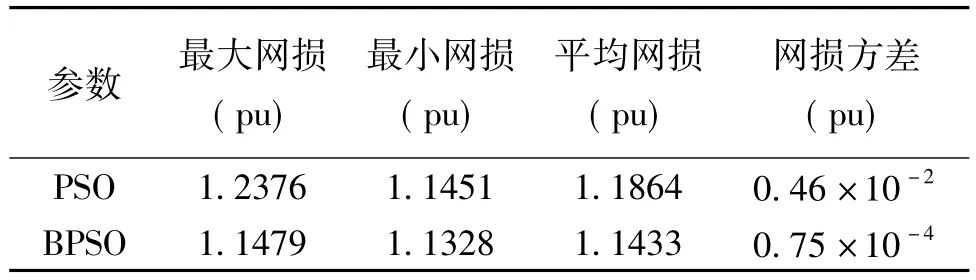
表4 无功优化结果(IEEE118)Tab.4 Reactive power optimization result(IEEE118)

从表4可以看出，当系统节点增多时，标准PSO算法陷入局部最优解的几率大大增加，算法的效率下降;而BPSO算法在多节点系统中仍有较好的表现，这是因为仿生机制增强了种群免于局部最优的能力。

6 结论

本文提出的仿生粒子群优化算法从生物特性出发，以个体的视角观察其他粒子并对大群体进行分组，在后期增强子群间的信息交流，不仅保证了全局搜索能力，而且维持了种群的多样性。对IEEE30节点和IEEE118节点系统进行仿真计算，结果表明该算法收敛精度高，全局搜索能力强，可有效应用于电力系统的无功优化。

［1］Abdul-Rahman K H，Shahidehpour S M.Reactive power optimization using fuzzy load representation［J］.IEEE Transactions on Power Systems，1994，9(2):898-905.

［2］Dai Chaohua，Chen Weirong，Zhu Yunfang，et al.Reactive power dispatch considering voltage stability with seeker optimization algorithm［J］.Electric Power Systems Research，2009，79(10):1426-1471.

［3］马继山，杨洪耕 (Ma Jishan，Yang Honggeng).基于内点法和改进粒子群算法的无功优化混合策略 (A hybrid strategy based on IPM and PSO for optimal reactive power flow)［J］.电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2010，29(4):48-51.

［4］崔挺，孙元章，徐箭，等 (Cui Ting，Sun Yuanzhang，Xu Jian，et al.).基于改进小生境遗传算法的电力系统无功优化 (Reactive power optimization of power system based on improved Niche genetic algorithm)［J］.中国电机工程学报(Proceedings of the CSEE)，2011，31 (19):43-50.

［5］李惠玲，盛万兴，张学仁，等 (Li Huiling，Sheng Wanxing，Zhang Xueren，et al.).小生境遗传算法在电力系统无功优化中的应用 (Application of improved Niche genetic algorithm in reactive power optimization)［J］.电网技术(Power System Technology)，2008，32 (17):29-34.

［6］曾令全，罗富宝，丁金嫚(Zeng Lingquan，Luo Fubao，Ding Jinman).禁忌搜索-粒子群算法在无功优化中的应用 (Application of particle swarm optimization algorithm integrated with Tabu search in reactive power optimization)［J］.电网技术 (Power System Technology)，2011，35(7):129-133.

［7］曾学强，刘志刚，符伟杰，等 (Zeng Xueqiang，Liu Zhigang，Fu Weijie，et al.).改进差分进化算法在电力系统无功优化中的应用 (Application of improved differential evolution algorithm in reactive power optimization)［J］.电网技术 (Power System Technology)，2012，36(2):121-125.

［8］姜慧兰，陈平，王敬朋，等(Jiang Huilan，Chen Ping，Wang Jingpeng，et al.).改进粒子群算法在电网无功优化中的应用 (Application of improved particle swarm optimization in power system reactive power control)［J］.中国电力(Electric Power)，2011，4(12):11-15.

［9］刘世成，张建华，刘宗岐 (Liu Shicheng，Zhang Jianhua，Liu Zongqi).并行自适应粒子群算法在电力系统无功优化中的应用(Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization of power system)［J］.电网技术 (Power System Technology)，2012，36(1):108-112.

［10］吴方劼，张承学，段志远(Wu Fangjie，Zhang Chengxue，Duan Zhiyuan).基于动态多种群粒子群算法的无功优化(Application of modified particle swarm optimization in reactive power optimization)［J］.电网技术(Power System Technology)，2007，31(24):35-39.

［11］王秀云，宋云峰，贾彦兵，等 (Wang Xiuyun，Song Yunfeng，Jia Yanbing，et al.).含维变异的量子粒子群算法在无功优化中的应用 (Reactive power optimization based on quantum-behaved particle swarm optimization with dimension mutation operator)［J］.电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2010，29(2):38-42.

［12］刘丽军，蔡金锭 (Liu Lijun，Cai Jinding).基于自适应强引导粒子群算法的电力系统无功优化 (Reactive power optimization based on adaptive induction-enhanced particle swarm algorithm)［J］.电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2012，31(4):24-28.

［13］Kennedy J，Eberharrt R.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks［C］.1995.1942-1948.

［14］许文超，郭伟(Xu Wenchao，Guo Wei).电力系统无功优化的模型及算法综述(Summarize of reactive power optimization model and algorithm in electric power system)［J］.电力系统及其自动化学报 (Proceedings of the CSU-EPSA)，2003，15(1):100-104.

［15］李丽，牛奔 (Li Li，Niu Ben).粒子群优化算法(Particle swarm optimization algorithm)［M］.北京:冶金工业出版社 (Beijing:Metallurgical Industry Press)，2009.27-29.

［16］Wu Q H，Cao Y J，Wen J Y.Optimal reactive power dispatch using an adaptive genetic algorithm［J］.International Journal of Electrical Power and Energy Systems，1998，20(8):563-569.

Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization of power system

WANG Xiu-yun1，LI Chao1，ZHAO Yu2，CHEN Ya-xiao2
(1.School of Electrical Engineering，Northeast Dianli University，Jilin 132012，China; 2.Liaocheng Power Supply Company，Liaocheng 252000，China)

Based on the particle sward optimization(PSO)，bionic particle sward optimization(BPSO)algorithm is presented in this paper which follows the biological feature of group optimizing.In the early period，group is dynamically divided into several subgroups，each of which is relatively independent and evolves towards one target.Members change rapidly as the procedure of evolution proceeds.The latter increases the exchange of information between subgroups，and so the algorithm converges faster.Not only can this algorithm enrich the variety of population and avoid converging the local optimal solution，but it can also attain a fairly high rate of convergence.In this paper，the algorithm is applied in the reactive power optimization of power system.Compared with the standard PSO，the algorithm is proved to be feasible and practicable through simulation of IEEE30 bus system and IEEE118 bus system.

power system;reactive power optimization;bionic;group;particle sward optimization

TM 712

:A

:1003-3076(2015)07-0075-06

2014-05-07

王秀云(1977-)，女，吉林籍，副教授/硕导，硕士，研究方向为电力系统优化运行;李 超(1988-)，男，吉林籍，硕士研究生，研究方向为电力系统无功优化。