发输电系统可靠性分析中最优切负荷模型

荣雅君，马秀蕊，杨 伟

(电力电子节能与传动控制河北省重点实验室，燕山大学电气工程学院，河北秦皇岛066004)

发输电系统可靠性分析中最优切负荷模型

荣雅君，马秀蕊，杨 伟

(电力电子节能与传动控制河北省重点实验室，燕山大学电气工程学院，河北秦皇岛066004)

电力系统可靠性分析的过程中系统状态分析环节最为核心，也最为费时，尤其是在状态抽样中用到枚举法或者蒙特卡洛模拟法时，需要进行大量的系统状态分析。本文提出切负荷量最小兼顾负荷重要度和区域就近削减负荷原则来进行负荷削减。重要度原则体现在削减负荷时按负荷级别进行削减，区域就近原则使得切负荷点不再在全系统范围内搜寻，大大减少了计算时间。通过IEEE-RTS79可靠性测试系统的计算结果可知，该法在减少计算时间方面有明显的优势，切负荷量也更切合实际情况。

电力系统可靠性;状态分析;最小切负荷量;区域就近原则;重要度原则

1 引言

电力系统可靠性分析已经成为电网规划决策中非常重要的一部分。电力系统的停电事故大部分是由于发电机组故障和输电线路故障引起的，目前对发输电电力系统可靠性评估的量化指标以切负荷量为主，因此对系统状态分析中切负荷进行优化是必不可少的环节。

发输电系统可靠性评估主要包括三部分:系统状态抽样、系统状态分析以及可靠性指标计算［1］。其中系统状态分析对选定的系统状态进行网络是否解列判断和潮流计算，从而确定是否需要进行负荷切除。目前，有文献使用最大流模型，利用网络特定状态下的最大流代替系统中的潮流分布，避免了负荷削减，计算速度快，但不满足基尔霍夫第二定律，只反映了元件故障后系统的最大可能响应极限，结果过于乐观［2］。还有文献中则只采用了粒子群算法等类线性规划算法对系统切负荷进行最优计算，又忽略了就近原则及重要度原则在实际系统切负荷中的作用。文献［3］中基于交流潮流的负荷削减非线性规划模型是一个精确的模型，但验证耗时并且编程复杂，对于大规模电力系统的长期规划不适合。在大规模电力系统中，元件故障通常只引起个别线路过载，因此没必要在全局范围内切负荷，寻求高效、可靠、计算时间与系统规模基本无关的负荷削减模型有重要意义［4，5］。锁定了切负荷区域，但并不能将该区域内所有负荷节点同等地切除，这就需要考虑负荷等级，一级负荷是不可以切除的，或者需要慎重切除。

基于以上切负荷中遇到的问题，本文基于直流潮流计算兼顾考虑了切负荷量最小、就近原则和重要度原则三个方面，通过IEEE-RTS79［6］可靠性测试系统验证了给出的可参考性模型的正确性。

2 最小切负荷计算及重要度模型

基于直流潮流模型，最优负荷削减就成为一个线性规划问题，目标函数为［7，8］:式中，NC为负荷母线所组成的集合;NG为发电机母线组成的集合;T(Sj)为状态Sj下的线路有功功率向量;A(Sj)为状态Sj下的线路有功功率向量和节点注入功率间的关联矩阵;PG为节点发电机注入有功功率向量;PD为节点有功负荷向量;X为负荷削减向量。

上述为不计负荷重要度时，线性规划全局最优切负荷方案。但是，在实际系统中，往往需要考虑负荷的重要度。一般，实际系统中将负荷按对供电可靠性的要求分为三级:

(1)第一级负荷。对负荷的中断供电，将可能造成生命危险、设备损坏，破坏生成过程，使大量产品报废，给国民经济造成重大损失，使市政生活发生混乱等。

(2)第二级负荷。对这一级负荷的中断供电，将造成大量减产，交通停顿，使城镇居民生活受到影响等。

(3)第三级负荷。所有不属于第一、二级的负荷，如工厂的附属车间、小城镇等负荷属于第三级负荷。

对第一级负荷要保证不间断供电;对第二级负荷，如有可能，也要保证不间断供电。反应到目标函数中，可以用加入权值αj的方法实现，上述目标函数变为:

式中，M为每条负荷母线上负荷被分为的等级;αj为该母线第j等级负荷对应的加权因子。

根据所有节点的各级负荷来确定各节点权重αj的原则如下:

(1)一级负荷最小值 ×权值＞二级负荷最大值×权值;

(2)二级负荷最小值 ×权值＞三级负荷最大值×权值 。

本文一共考虑了三个等级的负荷，若根据实际情况需要分为更多级别负荷，则可以此类推计算各级负荷的权重值。按照上面原则可以使得在最优值的搜寻过程中，按照事先设置的等级搜寻。如果各个级别的负荷都可以在需要的时候切除，则可按照上述原则即可实现。如果有负荷，比如第一级负荷不可以切除，则在权重确定时，除了满足上述原则外，可额外加大权重。

3 区域就近削减负荷原则

在发输电系统可靠性评估中，往往要模拟大量的系统状态，对每种状态都要进行切负荷运算。模拟抽样的大量系统状态中，有些会导致原本连接的母线断开，甚至有可能会导致系统解列，每条母线间彼此的远近程度也会发生变化。因此，以往按与故障元件距离远近来对每条母线设置权值，再进行线性规划计算的方法就不太便于实现。

本文提出区域就近削减负荷原则的方法来考虑按就近原则削减负荷。基本思想为:首先选出几个故障率最大的元件作为各自的区域;然后，根据实际情况，将这些元件附近的其他元件并入该区域，该区域也即为故障影响区域;最后，模拟每次系统状态时，如果需要切负荷，则根据故障元件所在的区域，在小范围内进行负荷削减。

以三机九节点简单系统来说明区域就近削减负荷原则的原理。图1为其系统图。

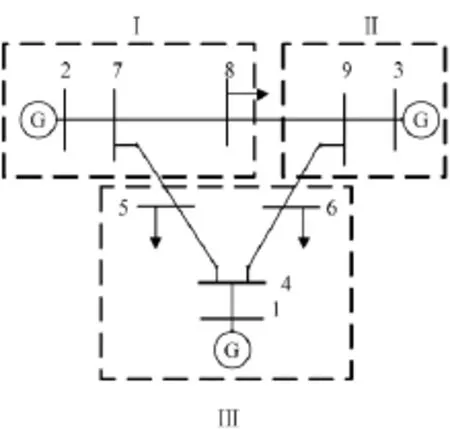
图1 三机九节点系统图Fig.1 Three generators and nine nodes system diagram

假设三个发电机为最易发生故障的元件，根据实际情况，如其发生故障，希望将影响控制到各自的区域内(如图1所示的三个区域)。如果Ⅰ区内的发电机发生故障，则只在Ⅰ区内的负荷节点作为目标节点，搜寻最优切负荷值。区域就近削减负荷原则的基本流程如图2所示。

因此，上述的目标函数式(7)中的NC也由母线数改为目标区域负荷母线数。目标区域的确定原则为:如果故障元件为单区域，则NC为单区域内负荷母线数量;如果为多区域，则NC为多个区域负荷母线总数;如果故障元件分布在各个区域，则NC为整个区域负荷母线总数。

区域就近削减原则不仅考虑了实际负荷削减的情况，同时当系统发生解列时，克服了由母线连接情况确定相互之间的远近程度的弊端，主要也为系统状态分析节省了很多时间。

图2 区域就近削减负荷基本流程Fig.2 Basic flow of area nearby load shedding

4 算例分析

IEEE-RTS79系统是一个24节点系统，该系统有32台发电机，33条输电线路，5台变压器，17个负荷节点，装机总容量为3405MW，系统最大负荷为2850MW。系统的电气参数和可靠性参数可以参考文献［6］。其区域划分图如图3所示。

算例中系统分为三个区域，对每个区域内的负荷节点都采用线性规划的方法计算切负荷量，兼顾重要度原则和区域就近原则。算例中，系统状态选择采用状态空间分割法［9，10］，即由快速排序法(FST)(上限概率取0.701)和蒙特卡洛模拟法(MCS)组成，模拟次数取20000次。系统结果用电力不足期望值(EDNS)指标来表示。

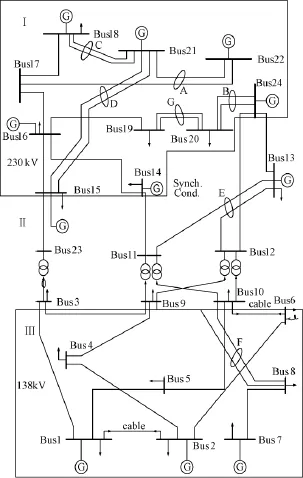
图3 IEEE-RTS系统结构图Fig.3 IEEE-RTS system structure

首先对系统切负荷只计及负荷重要度，以验证按重要度原则切负荷方法的正确性。为了便于观测方法的重要性，将15、16和18节点设置为一级负荷，是最后削减，并非不可削减;3、6、7、8、9和10节点设置为二级负荷节点;1、2、4、5、13、14、19和20节点设置为三级负荷节点。各负荷节点重要度权值如表1所示，计算结果如表2所示。

表1 各节点重要度权值Tab.1 Importance weight of nodes

由表2可以看出，节点15、16和18上的切负荷量转移到其他节点上;三级负荷节点中切负荷量的最小值也大于二级负荷切除的最大值，二级负荷节点的切除最小值也大于一级负荷节点中切除的最大值，实现了重要度原则的选择性。削减负荷的总量也与未计及重要度原则时相差不多。因此，按照重要度权值设置原则设置的权值，能够很好地将系统切负荷量按重要度来规划。

在重要度的基础上加入区域就近原则，即在每次系统状态分析时在区域内进行，这样大大减少了计算时间。计算结果如表3所示。

表3第二列为系统划分为三区的计算结果，每区负荷节点数为6个左右，缩短了计算时间。

表3中四区分两种情况，第一种情况，较平均分配，每区能分到4个节点左右;第二种情况是将第2区节点增加。由强迫停运率可得，第2区故障率比较高，因此若按第一种情况分为四区，则第2区内有4个节点，此时由表3可知，节点9切负荷量异常高，这是因为第2区负荷节点偏少，不能使最小切负荷量达到最优。当把节点8由第4区改为第2区时，则切负荷量明显降低，节点9的负荷削减量也明显降低。将四区与三区结果相比也可以发现，四区的EDNS总量明显大于三区EDNS总量，这表明，就近原则与最小切负荷量是相互矛盾的，划分区域越多，越不能实现最小切负荷的寻优，因此，区域划分既要考虑切负荷最小，又要考虑计算时间。虽然分区越多，计算时间会相对减少，但是相差不多，这是因为分区越多，每次负荷寻优节点相对减少，时间会相对减少，但是故障区域会增加，多个区域相加，总的负荷节点反而会增多。因此，总体来说，分成三区和四区计算时间不会相差太多，应仍以削减负荷量为主要衡量指标。由表2和表3中的切负荷总量可以得出，算例中将系统划分为三区比较合适。

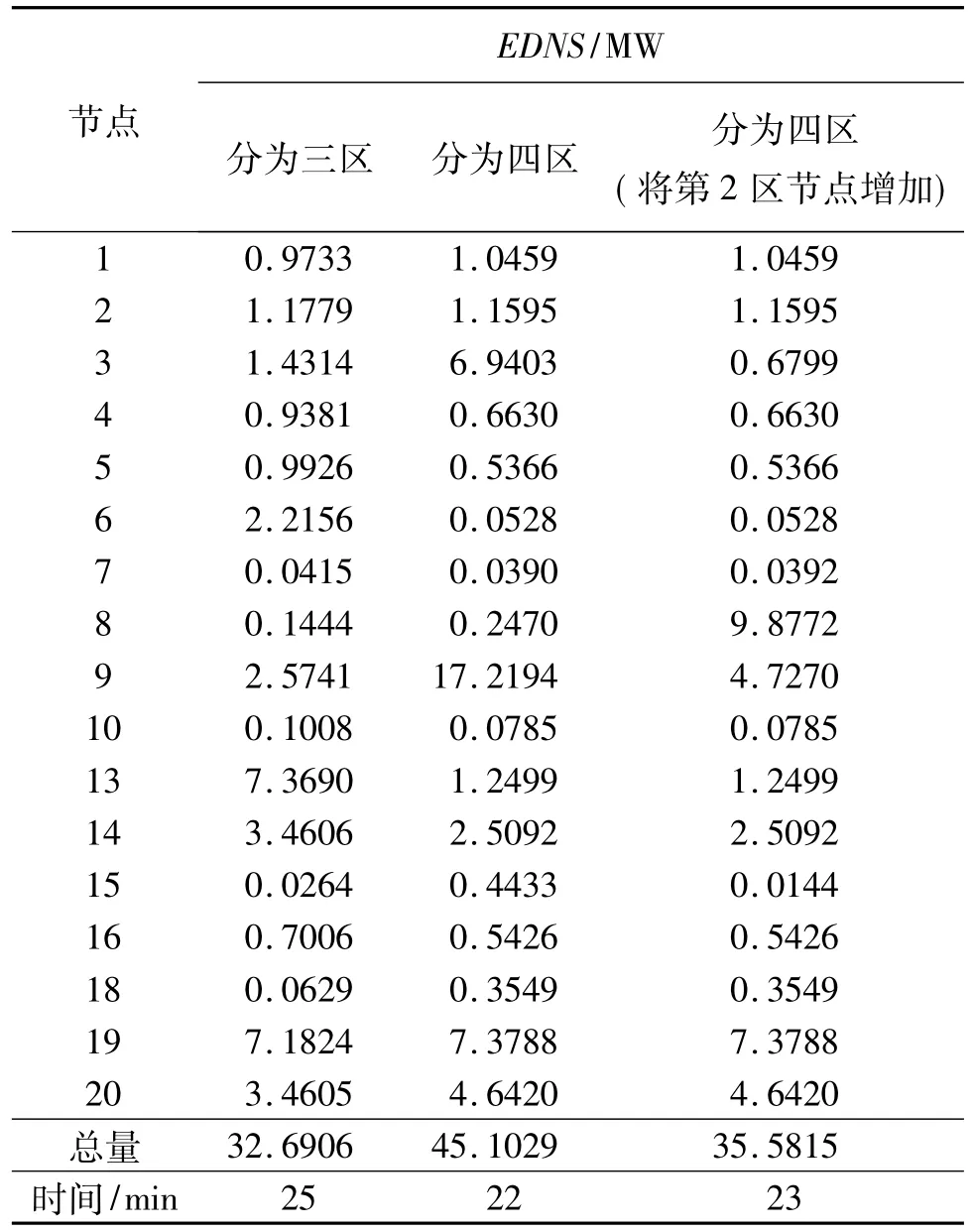
表3 考虑区域就近原则计算结果比较Tab.3 Comparison of calculation results considering areas nearby principle

5 结论

本文利用状态空间分割法进行系统状态抽样，在系统状态分析中运用线性规划兼顾重要度原则和区域就近削减负荷原则，使得切负荷量在三者之间得到最优值，其优点如下:

(1)按重要度原则削减负荷，将实际系统中的负荷重要度引入，能够较真实地反应各个节点的可靠度，为节点切负荷量提供了依据;

(2)区域就近削减负荷原则能够大量缩短计算时间，也使得故障影响区域能够在最优的基础上兼顾实际需要，将故障影响区域控制在小范围内;

(3)将线性规划、重要度原则和区域就近削减负荷原则结合起来，不仅有利于计算，也使计算结果更具有实际意义。

［1］孙元章，程林，何剑，等(Sun Yuanzhang，Cheng Lin，He Jian，et al.).电力系统运行可靠性理论 (Power system reliability theory)［M］.北京:清华大学出版社(Beijing:Tsinghua University Press)，2012.89-124.

［2］赵渊，周家启，谢开贵，等 (Zhao Yuan，Zhou Jiaqi，Xie Kaigui，et al.)，基于网流规划的发输电组合系统可靠性评估模型研究 (Study on reliability assessment model of composite generation and transmission system based on network flow programming)［J］.电网技术(Power System Technology)，2003，27(10):21-24.

［3］Billinton R，Wenyuan Li.Reliability assessment of electrical power system using Monte Carlo methods［M］.New York:Plenue Press，1994.

［4］Shandilya A，Gupta H，Sharma J.Method for generation rescheduling and load shedding to alleviate line overloads using local optimization［J］.IEE Proceedings CGeneration，Transmission and Distribution，1993，140 (5):337-342.

［5］Shah S，Shahidehpour S M.A heuristic approach to load shedding scheme［J］.IEEE Transactions on Power Systems，1989，4(4):1421-1429.

［6］IEEE APM Subcommittee.IEEE reliability test system［J］.IEEE Transactions on Power Apparatus and Systems，1979，PAS-98(6):2047-2054.

［7］赵渊，周家启 (Zhao Yuan，Zhou Jiaqi).发输电组合系统可靠性评估的最优负荷削减模型研究 (A heuristic approach to local load shedding scheme for reliability assessment of composite generation and transmission system)［J］.电网技术 (Power System Technology)，2004，28(10):34-37.

［8］赵晋泉，叶君玲，邓勇 (Zhao Jinquan，Ye Junling，Deng Yong).直流潮流与交流潮流的对比分析 (Comparative analysis on DC power flow and AC power flow)［J］.电网技术 (Power system technology)，2012，36 (10):148-151.

［9］何剑，孙华东，刘明松 (He Jian，Sun Huadong，Liu Mingsong).基于扩展状态空间分割法的含风电场电力系统运行备用风险评估 (Extended state-space partitioning based operating reserve risk assessment for power grid connected with wind farms)［J］.电网技术 (Power System Technology)，2012，36(3):258-259.

［10］贾燕冰，严正(Jia Yanbing，Yan Zheng).基于改进快速排序法的发电系统可靠性评估 (An improving fast sorting technique for generating system reliability evaluation)［J］.电网技术 (Power System Technology)，2010，34(6):145-147.

Model of optimal load shedding program for reliability assessment of composite generation and transmission system

RONG Ya-jun，MA Xiu-rui，YANG Wei
(Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province，School of Electrical Engineering，Yanshan University，Qinhuangdao 066004，China)

In the process of power system reliability analysis，the system state analysis is the most important and the most time consuming.Especially，it needs a lot of system analysis，when the state sampling uses the enumeration method or Monte-Carlo simulation method.This paper proposed the method of the minimum load shedding according to the load important degree and area nearby principle.Importance principle reflected that in cutting load the reduction is in accordance with the load level，making load cutting more close to the actual cutting load conditions.Area nearby principle makes the cutting load point is no longer extending to the scope of the whole system，greatly reducing the computing time，and makes cutting load in the area more likely to get the optimal value.The calculation and analysis results from such reliability test system of an IEEE-RTS79 show that the method of the load shedding has obvious advantages in reducing computing time，and load shedding is also more practical.

power system reliability;system state analysis;minimum load shedding;area nearby principle;importance principle

TM744

:A

:1003-3076(2015)07-0058-05

2014-06-03

中国南方电网公司科技项目(K-YN2012-018)

荣雅君(1957-)，女，吉林籍，教授，硕士，研究方向为电力系统继电保护和微电网新能源等;马秀蕊(1989-)，女，河北籍，硕士研究生，研究方向为含新能源的电力系统可靠性研究。