天然异龄林资产评估起测直径提高的可能性研究

林进添郑德祥

（1．福建江夏学院，福建福州350108；2．福建农林大学林学院，福建福州350002）

天然异龄林资产评估起测直径提高的可能性研究

林进添1郑德祥2

（1．福建江夏学院，福建福州350108；2．福建农林大学林学院，福建福州350002）

利用可拓共存度分析法与线性约束分析法，探讨天然异龄林评估资产核查起测直径提高的理论可能性。结果表明：只要能保证平均每厘米起测直径升幅的蓄积量平均误差足够小，就存在提高起测直径的可能；并以丰富的样地数据资料证实了天然异龄林因其直径分布结构特点而具有提高起测直径的现实可能。

天然异龄林；资产核查；起测直径；可拓共存度；线性约束

森林资源资产评估中的资产核查关键在于客观反映林分生长因子情况，最重要的是保证蓄积量和出材量测算的精确度。一方面资产核查调查精度和外业工作量取决于调查方法选择，另一方面与起测直径息息相关。起测直径偏小，大量小径阶树木纳入检测范围，外业调查工作量大，且由于受小径阶木数量多的影响，林分平均胸径可能被低估而无法客观反映采伐量和出材规格；若起测直径过大，虽能将一部分林木踢出检量范围，大大降低了外业调查工作量，但平均胸径有可能因此被高估，极易因漏测诸多中小径阶林木导致蓄积量和出材估算的不准。

天然异龄林林分具有复林层、多树种、年龄差异大等特点，这样复杂多样的生境结构给森林资源资产评估资产核查工作的调查精度和外业工作量两方面带来了难题与挑战。现行林业调查技术规定都将乔木树种的起测直径确定为5 cm，但天然异龄林林分在该起测直径下外业调查工作量大，又有可能因小径木的影响无法客观反映林分可采伐资源和出材情况。这是因为天然异龄林直径分布呈典型的倒“J”型分布，小径阶林木株数多，但其蓄积占林分总蓄积的比重相对较小，出材量和出材规格主要取决于中大径阶林木。因此，适当提高天然异龄林林分的起测直径是解决该问题的途径之一。但是，提高起测直径是否有内在可能尚未有人给出合理解释。故研究天然异龄林评估资产核查的合理起测直径，有利于完善天然异龄林评估资产核查技术，对天然异龄林资产评估体系的发展具有重要意义。

1 起测直径提高的理论可能性

1.1 可拓共存度分析

可拓学是1983年由中国学者蔡文提出的一门原创性横断学科，《可拓集合和不相容问题》的发表标志着可拓学的诞生。可拓学以形式化的模型探讨事物拓展的可能性以及开拓创新的规律与方法，并用于解决矛盾问题。可拓论引入了物元的概念，该思维过程既能描述量变又可以考察质变。其将客观世界作为一个物元世界，因此处理客观世界中的矛盾问题随之转化为处理物元之间的矛盾问题。事物具有各种各样的特征，确定了事物关于某一特征有一定的量值，描述事物的基本要素主要有事物的名称、特征和量值。物元就是利用名称、特征和量值来表示事物的，它是表征事物的一种基本单位。总体层次上，可拓理论运用基元形式化的手段来描述物、事及关系，其中物元表示物，事元代表事，关系元则表明事物彼此之间的关系［1－4］。

1.1.1 可拓模型构建 起测直径提高的研究其实就是研究下面的问题：提高起测直径到一定水平的条件下，同时达到减少外业调查工作量和保证林分调查质量的双目标。对此问题，依据可拓学理论作出如下的可拓模型：

将起测直径提高Δd0cm，则有：

目标G1＝［保证，支配对象，林分调查质量］目标G2＝［减少，支配对象，外业调查工作量］条件l＝［提高，支配对象，起测直径程度，Δd0］所以，研究问题转化为M0＝（G1∧G2）*l的形式化表达。

资产评估活动的资产核查中保证林分调查质量最重要的是保证蓄积量和出材量测算的精确度。因此，林分调查精度（P）主要由蓄积量调查精度（PV）和出材量测算精度（P)V）2部分构成，假设有：式中：a和b为两者的精度贡献系数，符合归一化条件。

另记σV为起测直径提高Δd后平均1 cm升幅的蓄积量平均误差，则有：

同理，记σ)V为起测直径提高Δd后平均1 cm升幅的出材量平均误差，则有：

则有：

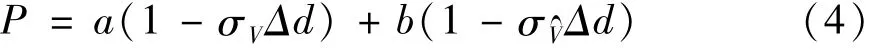
简化为：

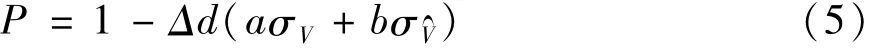
所以存在目标：

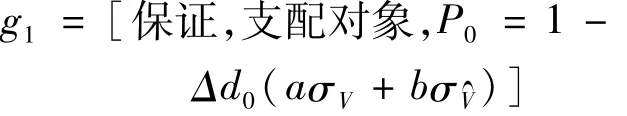
使得g1⇒G1，符号“⇒”表示蕴含关系。

起测直径的提高，将部分小径阶林木剔除出检测范围，相应地降低了外业调查工作量。假设减少的株数为：

所以存在目标：

g2＝［减少，支配对象，株数，程度，N0＝¯NσNΔd0］

使得g2⇒G2。

因此，问题M＝（g1∧g2）*l为问题M0＝（G1∧G2）*l关于目标（G1∧G2）的蕴含问题，也是M0的核问题。

1.1.2 共存度判定 无论是林业规划调查还是森林资源资产评估作业，林分调查精度都有一个下限的要求值，可设为。因此，区间[，100% ]为林分调查精度P的量值域，提高起测直径减少的林木株数N的量值域理论上为 [ 0，¯N]，据此可以分别建立P和N的简单初等关联函数：

则k(M)＝k(P)k(N)称为问题M的共存度。若在条件l下目标g1和g2无法同时实现，此时为不相容问题，记为(g1∧g2)↑l。而要使在条件l下目标g1和g2能同时实现，记为 (g1∧g2)↓l，则需有：

即：

实际上，在条件l下目标g2肯定能实现，所以k（N0）＞0，因此式（10）成立只需：

简化可得：

出材量是蓄积与出材率的乘积。理论上有了出材率的缓冲，在相同的起测直径提高水平下出材量的变化敏感度不会大于蓄积的敏感度，所以σ)V≤σV，则：

1.2 线性约束分析

1.2.1 线性约束模型构建 假设Q为林分调查的工作质量效果，是追求的目标，数值越大，表明调查质量效果越优。它由调查精度P和提升的外业调查效率W 2部分组成，即目标函数为：

其中：P＝aPV＋bP)V，符号意义同上文；W＝θΔd，θ表示起测直径每提高1 cm的工效增加系数，与直径分布情况有关，显然θ＞0；α和β为调查精度P和提升的外业调查效率W的效果贡献系数，符合归一化条件。

起测直径提高的可能性转化为如下的线性约束模型：

1.2.2 解线性约束模型 先画出约束条件L1和L2所围成的可行区域，见图1的阴影部分。

由于σ)V≤σV，所以直线PV比P)V陡，表示着在相同的起测直径提高水平下蓄积量的变化较敏感。下面根据约束条件L3的可能情况分别求解线性约束模型：

1）当直线W的斜率θ≤图1中点G与原点连线的斜率时（如图2中的直线W1和W2），即θ≤kOG。此时图2中的可行区域与图1的阴影部分相同。

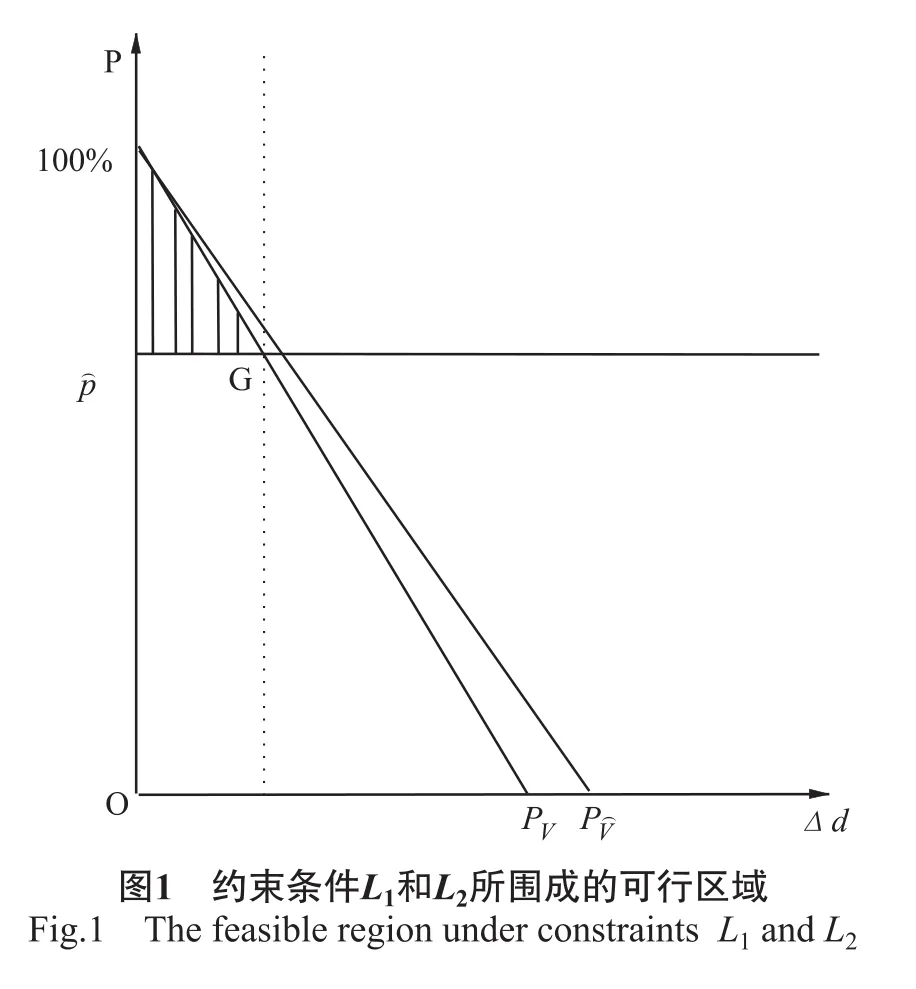
显然，目标直线Q的斜率只有小于直线PV的斜率才有可能取得最优解，则即：＞σV。将直线Q往右上方平移至点G时，直线Q与原点的距离最大，取得最大值。设点G坐标为( Δd0，)，其位于直线PV上，则有：

可得：

此时：

2）当直线W的斜率θ大于图1中点G与原点连线的斜率时，即θ＞kOG，如图3中的直线W3。直线W3与直线PV相交于点S，此时可行区域缩小至如图3。

同样，目标直线Q的斜率只有小于直线PV的斜率才有可能取得最优解。将直线Q往右上方平移至点S时，直线Q与原点的距离最大，取得最大值，见图4。

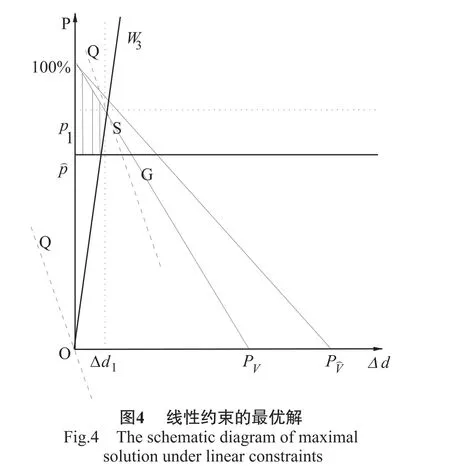
设点S坐标为（Δds，ps），其位于直线PV上，则有：

可得：

因为此时ps＞，所以1－ps＜1－，则有：

此时，

2 起测直径提高的现实可能性

2.1 数据资料来源与预处理

所用数据资料为福建省森林资源连续清查天然异龄林样地，共102块，均为阔叶混交或纯林。依据我国现行一、二类调查技术规定都将乔木树种的起测直径确定为5 cm，且将14 cm以上划为分中、大径级组［5－6］，因此，将各样地分别在起测直径5、6、7、8、9、10、11、12 cm和13 cm，按2 cm为一个径级、分径阶统计株数。由于36 cm径阶以上林木相对很少，且其中可能多个径阶无株数分布，为便于研究将胸径在35 cm及以上的统一归入36 cm径阶。按照不同起测直径情况，分别计算各样地的平均胸径、蓄积量、商品材出材量等，以起测直径5 cm时的统计数据作为起测直径研究的评价材料。

2.2 现实可能性的验证分析

森林资源连续清查的固定样地面积比较小（为0．066 7 hm2），各样地的实际直径分布可能不连续，为了得到天然异龄林的完整结构特征，首先将102个样地合并为1个6．8 hm2的大样地，分析其直径的分布规律，见图5。

从图5可看出，株数随径阶的直径分布是典型的倒“J”型分布。利用6．8 hm2的大样地数据统计发现，占总株数约10%的中大径级林木的蓄积比例为52．66%；占总株数约20%的中大径级林木蓄积比例为72．35%。为了作进一步分析，根据样地序号大小将总共102个样地按顺序分成6组（每组17个样地），合并为6个1．13 hm2的样地。统计结果显示：6个样地，占总株数在10%左右的中大径级林木的蓄积比例分别为53．12%，55．18%，55．83%，54．58%，53．56%，55．21%，平均为54．58%；占总株数在20%左右的中大径级林木蓄积比例分别为72．79%，69．80%，73．62%，73．86%，75．85%，74．79%，平均为73．45%。汇总的大样地、6个小样地的统计结果彼此差异不大，基本上可以得出如下结论：天然异龄林中占总株数10%的中大径级林木提供了接近55%的活立木蓄积，占总株数20%的中大径级林木所占蓄积接近75%。而前人相关研究认为，热带天然林中占总株数20%以下的大径级林木提供了80%以上的活立木蓄积［7］。虽然结论稍有出入，但是均表明天然异龄林林分蓄积量和出材量主要取决于占株数比例很小的中大径级林木，这是由其独特的倒“J”型直径分布结构所决定的。根据森林资源调查技术规定，林分优势树种的确定是根据占蓄积比例65%的标准来划分的，其他有关的林分特征因子，诸如平均胸径、平均树高则是与优势树种相对应的［8］。因此，天然异龄林中占蓄积65%以上的中大径级林木一定程度上可以代表整个林分的相关属性因子。天然异龄林中仅占总株数20%的中大径级林木所占蓄积已接近75%，远高于65%。所以从客观描述林分生长状况和质量的立场来看，合理提高天然异龄林起测直径，将部分小径木剔出检测范围，是存在着现实可能性的。

在6～13 cm起测直径水平下，分别计算102块样地的单位面积蓄积量，并以起测直径5 cm时的统计数据作为比较基准，计算各起测直径水平的单位面积蓄积量平均误差，从而确定σV值。分别取最低调查精度85%和90%，结果见表1。

表1 不同起测直径的σV值Tab．1 TheσVvalue under the differentMMD

3 结论与讨论

天然异龄林评估资产核查作业中，起测直径的提高具有深远的实践意义。分别建立可拓模型和线性约束模型，利用可拓共存度分析和求取线性约束最优解，理论上科学阐述了天然异龄林评估资产核查起测直径提高的可能性。只要能保证平均1 cm起测直径升幅的蓄积量平均误差σV足够小，即满足，就存在提高起测直径以降低外业工作量且保证林分调查质量的可能。丰富的样地数据资料分析，同样证实了天然异龄林因其直径分布结构特点而具有提高起测直径的现实可能。

适当提高天然异龄林资产评估中的资产核查起测直径，无疑是具有进步意义的。但本研究仅考虑了保证核查精度和降低外业调查工作量两个要求，也只采用了可拓共存度和线性约束模型对起测直径提高的理论可能性作了初步的探讨和判断，起测直径提高要成为普遍行业共识和可行森林调查技术，还需要从其他角度要求、结合更为先进的科学原理进行论证。本研究应用了102块阔叶林和阔混交林样地探讨了起测直径提高的现实可能性，为了验证起测直径提高的普遍适用性，未来应利用不同树种类型、不同区域范围的天然异龄林样地数据作进一步验证分析。当然，最为关键的是天然异龄林起测直径可以提高到何种程度，亟须进一步的研究分析和综合判定。

［1］ 杨春燕，蔡文．可拓工程［M］．北京：科学出版社，2007．

［2］ 蔡文，杨春燕，陈文伟，等．可拓集与可拓数据挖掘［M］．北京：科学出版社，2008．

［3］ 黄金才，陈文伟．可拓数据挖掘的概念与理论［J］．计算机工程与应用，2006（14）：7－8．

［4］ 蔡文，杨春燕，何斌．可拓逻辑初步［M］．北京：科学出版社，2003．

［5］ 牛丽丽，余新晓，刘彦，等．不同起测胸径对判定油松分布格局的影响［J］．北京林业大学学报，2008，30（2）：12－16．

［6］ 李丽，惠淑荣，惠刚盈，等．不同起测径对判定林木空间分布格局影响的研究［J］．林业科学研究，2007，20（3）：334－337．

［7］ 陆元昌．近自然森林经营的理论与实践［M］．北京：科学出版社，2006．

［8］ 曾伟生．关于异龄林大小等级划分标准的探讨［J］．中南林业调查规划，2009，28（3）：8－10．

（责任编辑 张 坤）

Study on Possibility of Raising Minimum Measured Diameter for Natural Uneven-Aged Forest Among Assets Verification

Lin Jintian1，Zheng Dexiang2

（1．Fujian Jiangxia University，Fuzhou Fujian 350108，China；2．Fujian Agriculture and Forestry University，Fuzhou Fujian 350002，China）

In this paper the theoretical possibility of raising theminimum measured diameter among assets verification for natural uneven-aged forest was discussed through extension coexist degrees and linear constraintsmethod．The result showed that there was the possibility of raising theminimum measured diameter under this condition that average error of stock volumewas sufficiently ensured as small as possible．And the reality of raising theminimum measured diameter for natural uneven-aged forestwas confirmed，because of its diameter distribution characteristics，by using rich plot data．

natural uneven-aged forest；assets checking；minimum measured diameter；extension theory；linear constraints

S757．2

：A

：2095－1914（2015）06－0060－06

10．11929／j．issn．2095－1914．2015．06．010

2015－04－06

福建省社会科学规划项目（2014C039）资助。

第1作者：林进添（1986—），男，博士，讲师。研究方向：森林资源资产评估、森林资源审计与认证。Email：393668306＠qq．com。