地下热流固耦合对EGS热开采的影响*
2015-06-01曹文炅黄文博蒋方明
曹文炅,黄文博,蒋方明
(中国科学院广州能源研究所,广州 510640)
地下热流固耦合对EGS热开采的影响*
曹文炅,黄文博,蒋方明†
(中国科学院广州能源研究所,广州 510640)
人工热储的孔隙率及渗透率在增强型地热系统(EGS)地下热开采过程中受温度(T)、水力(H)、应力(M)的综合影响。本文建立了EGS热开采过程THM耦合的三维计算模型,并采用局部非热平衡假设处理液岩对流换热。对一理想的五口井EGS系统采热过程进行了THM模拟计算,分析了岩石温度、孔隙压力对岩石应力场的作用机理,进一步研究了应力场对EGS采热性能的影响。结果表明,开采过程中岩石应力场为热储内孔隙压力和温差综合作用的结果,由孔隙压力造成的岩石应力为压应力,仅集中于注入井附近,由岩石温度变化引起的热应力为拉应力,随着热开采区域的扩展而扩展。液−岩温差是触发工质与岩石热交换的动因,同时也是产生热应力的根本。
增强型地热系统;局部非热平衡;热流固耦合;变物性
0 引 言
赋存于地下3~10 km范围的干热岩(Hot dry rock, HDR)地热能,因其清洁可再生性和空间分布的广泛性,已成为位居水力、生物质能之后的世界第三大可再生能源[1]。增强型地热系统(Enhanced geothermal systems, EGS)旨在将HDR地热能提取至地上并加以利用。EGS的原理是通过水力激发等手段,在低渗透性的HDR内产生具有一定连通性的裂隙网络,形成人工热储。然后由注入井灌注冷流体工质,流体工质流过地下裂隙时获取HDR热量,热流体经由生产井开采出来后用于地面发电,发电后的流体工质经进一步梯级利用降温后再回注至地下热储,从而形成循环生产。地下采热过程是EGS的关键,直接影响EGS的产能和寿命,而这一过程则包含了复杂的多物理场、多尺度综合效应。研究热储内热(Thermal, T),水力(Hydraulic, H),应力场(Mechanical, M)耦合作用对揭示EGS地下热开采机理,合理高效地获取HDR热能等具有重要意义。
在EGS热开采过程中,循环工质温度和压力的变化将改变其热物性,从而影响采热过程中工质流体的输运和岩石−流体换热。在水力及热力作用下高温岩体则发生有效应力场改变和骨架变形,进而导致岩石的储渗能力发生变化。这些变化反过来又影响循环工质的渗流,影响热量的输运,即会影响EGS的寿命、出力等生产指标。KOH等[2]结合有限元和随机生成裂隙构建了二维热储的THM耦合模型,研究表明高温岩体所受热应力能够在长期开采中影响热储渗透率,进而影响温度场分布和生产井采出温度。GHASSEMI等[3]研究了热应力对裂隙滑移和扩张的效应,并在后续研究中逐步增加了孔隙压力效应[4]、化学反应及矿物质溶解/沉积效应[5]。JEANNE等[6]将商用软件TOUGH与FLAC3d结合,进行了Geysers地热田的THM计算,并将位移计算值与Geysers项目试验观测的地表位移进行对比。MCDERMOTT等[7]研究了结晶岩体裂隙开度的热响应问题,认为裂隙的开度直接与裂隙平面的法向张应力相关。然而,在现有的研究中,对液−岩换热的处理通常采用局部热平衡假设,忽略了液−岩温差,由工质物性的变化引起的效应也鲜有报道。
本文根据热储层岩石中THM耦合的影响机理,考虑水的热物性温度和压力而变化的情况,从饱和多孔介质单相流体角度出发,建立了EGS热开采过程THM耦合的三维计算模型。对一理想的五口井EGS系统采热过程进行了THM计算,分析了岩石温度、孔隙压力对岩石应力场的作用机理,并探讨液−岩温差与岩石热应力的相关性,进一步研究了应力场对EGS采热性能的影响。
1 EGS热开采过程的热流固耦合模型
1.1 主控方程
本文在前期EGS采热过程数值模型工作基础上引入应力场计算部分[8-12]。模型基于局部非热平衡思想,采用两个能量方程来分别描述热储内流体和岩石骨架的温度场,可方便地处理采热过程中实际存在的岩石−流体换热过程。对于应力场的计算本文采用HU等[13]的平均总应力模型,该模型能够通过标量控制方程进行描述,可实现与流场及温度场计算的强耦合。模型将EGS的地下部分处理为三个性质不同的子区域:①开放流道性质的注入井和生产井; ②多孔介质性质的热储;③渗透性可忽略不计的热储周围岩体。模型假设单相流体流动,不考虑循环流体与岩石的化学作用。采用的控制方程如下。
循环工质的连续性方程:

循环工质的动量守恒方程:

岩石的能量守恒方程:
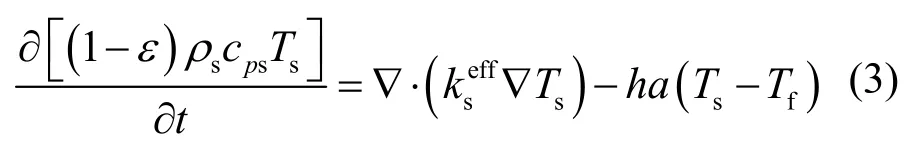
循环工质的能量守恒方程:

岩石的平均总应力方程:

其中,u、p、Tf、Ts及σm分别表示工质速度矢量、工质压力、工质温度、岩石温度及岩石平均总应力,为THM模型的主要求解变量;ρf、cpf、kf、μ分别表示工质密度、比热容、有效导热系数和动力粘度,受工质的温度和压力决定,将通过后续变物性模型给出变量随温度和压力变化的关系;g为重力加速度;ε和K分别为热储的孔隙率和渗透率,下文中将通过等效应力模型进行描述;ha表示岩石−流体对流换热强度,本文取ha=1.0 W·m−3·K−1;下标s和f分别代表岩石和流体,上标eff表示有效物性。式(5)中υ、α、β、B分别表示岩石的泊松比、Biot数、线膨胀系数以及体积模量;F为热储所受外力。
1.2 水工质的变物性模型
本文采用国际水及蒸汽物性组织(IAPWS)[14]建立的公式进行水工质的变物性模型建立。IAPWS模型针对水不同的相建立了相应的区域和方程,考虑到EGS系统中水的温度和压力范围(压力低于100 MPa,温度低于623.15 K),本文选用I区域(液相区域)进行建模。该区域采用Gibbs自由能描述水的状态:
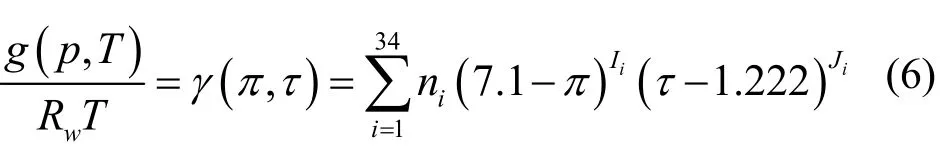
其中,g(p, T)为Gibbs自由能;Rw为水的比气体常数,Rw=461.526 J·kg−1·K−1;π与τ分别为无量纲化的压力和温度,π=p/p* , τ=T*/T ,参考压力 p*=16.53 MPa,参考温度T*=1 386 K;ni、Ii、Ji均为常数,可参考文献[14]。利用Gibbs自由能的偏导数,就可得到随温度和压力变化的密度及比热容。
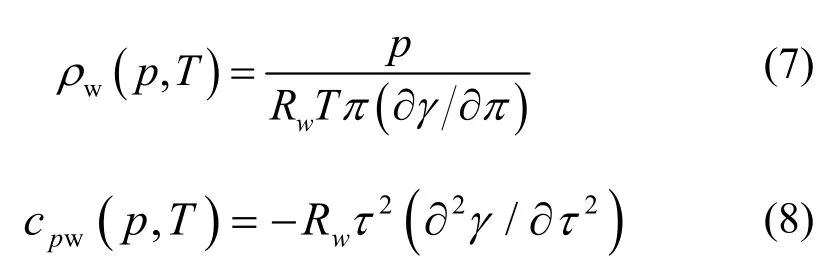
导热系数和粘度系数则由下述多项式给出[15-16]:

其中,参考值λ*=1.0 × 10−3W·m−1·K−1,μ*=1.0 × 10−6Pa·s;及为无量纲温度及密度, 可表示为=T/ T'及=ρ/ ρ',参考值T'=647.096 K,ρ'=322.0 kg·m−3;方程中下标0、1和2的关联项分别为稀释气体项,有限密度项及临界点修正项。导热系数及粘度系数的稀释气体项和有限密度项可由下列各式计算:


式中,Li、Lij、Hi及 Hij均为常系数,取值可由文献[15-16]查得。由于热储内的温度没有达到水的临界点,因此本文计算中取
1.3 THM耦合模型的实现
本文采用Fluent进行控制方程的求解,其中能量守恒方程、平均总应力方程均以标量控制方程进行计算,THM耦合机制如图1所示。热流两场之间的耦合由工质的变物性模型实现。热储层的孔隙率及渗透率是渗流及传热的关键参数,也是应力场与热、流计算耦合的关键。在岩土力学中孔隙率及渗透率可表示为岩石有效应力的相关函数,本文采用的计算模型如下[17-19]:
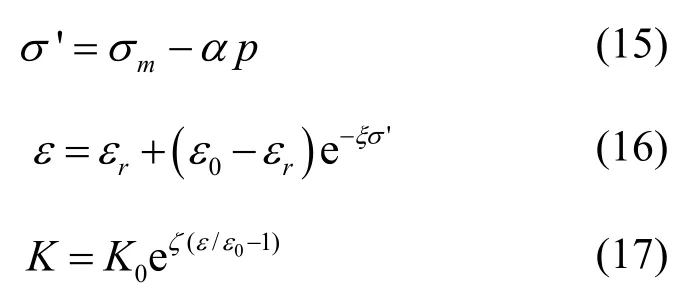
其中,σ'为岩石有效应力,0ε及rε分别为在零有效应力及高有效应力状态下的孔隙率;K0为初始孔隙率;ξ与ζ均为与材料相关的常系数。
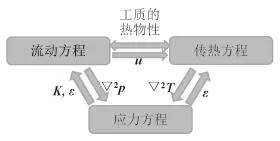
图1 THM耦合机制Fig. 1 Mechanism of the THM coupling
2 算例分析及讨论
2.1 计算模型
图2为某假设五口井分布EGS,由于对称性取1/4进行计算。人工热储的体积为500 m × 500 m × 500 m的立方体。热储周围包覆有足够体积的基岩和盖岩,避免了人为设定的边界条件带来的误差。注入井和生产井均为0.2 m × 0.2 m的方形通道。岩石的初始温度按照4 K/100 m的地温梯度随深度线性增加,地表温度设为300 K,热储中裂隙流体初始温度与当地岩石温度相同。所有与流体接触的壁面均为非滑移边界,注入井与生产井均采用定压力边界,注入井与生产井压差取10 MPa,热储内环境压力取40 MPa。注入温度为343 K,其余计算参数列于表1,计算模型的几何尺寸设置如图2所示。
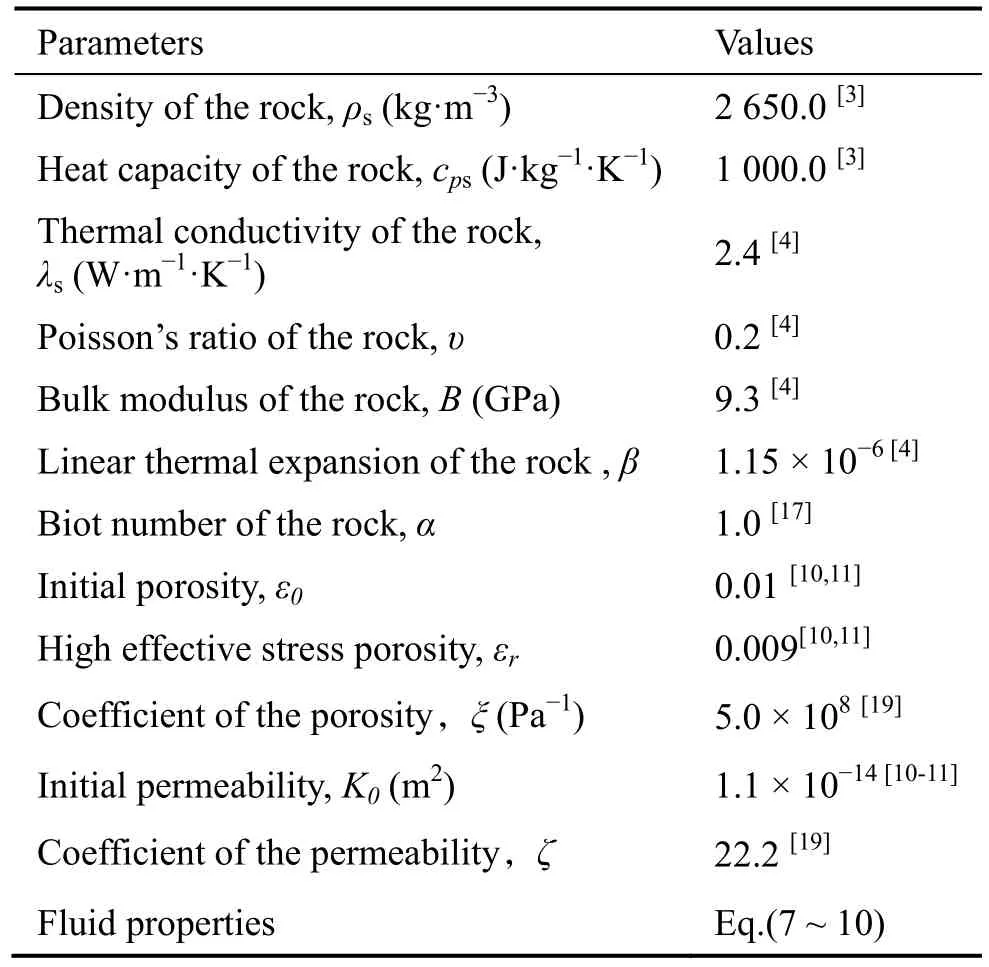
表1 模型计算参数Table 1 Parameters of the THM model

图2 五口井EGS模型几何尺寸Fig. 2 Geometrical dimensions of the considered quintuplet EGS
2.2 热开采过程温度场及渗流场对应力场的影响
图3显示了采热过程中热储内岩石温度随时间的变化。注入井附近岩石热量首先被采集,温度迅速降低。随着时间的推移低温区域逐渐向生产井一侧扩展。由于五口井分布的对称特征,热储内工质的流动以注入井为中心向四周扩展,温度采集前沿位置为近似的柱面。
图4显示了热储内孔隙压力随时间的变化。由图可知在整个开采阶段孔隙压力分布变化较小,高压区域集中于注入井附近。注入井附近压降极大,表明循环工质的动量损失主要集中在注入井附近。
图5显示了岩石平均总应力空间分布随热开采进行的发展情况,其量级和分布与文献[5,13]具有一致性:在非常接近注入井的区域平均总应力为正值,根据岩土力学中压应力为正的约定可知注入井附近的岩石受压应力作用。而在热储层内还存在着一个从注入井随开采的进行逐渐向生产井发展的拉应力区域(平均总应力为负值),该区域随着热开采的进行逐渐向注入井扩张。
岩石平均总应力是孔隙压力和岩石热应力综合作用的结果,为了说明孔隙压力和温度场对应力计算的影响,图6中提取并对比了开采至第5年时由孔隙压力引起的岩石应力及温度变化引起的岩石应力,即孔隙弹性应力及热弹性应力。
由图6可知,由孔隙压力造成的岩石应力为压应力,仅集中于注入井附近,由岩石温度变化引起的热应力为拉应力,随着热开采区域的扩展而扩展。从应力幅值来看,孔隙弹性应力幅值大于热弹性应力幅值,说明在注入井附近孔隙弹性应力起主导作用。热弹性应力作用相对较弱,但其空间分布大于孔隙弹性应力,并随着热开采进行不断扩展。为了进一步研究液−岩温差对热应力计算的影响,我们提取了图6b所示AB路径的液−岩温差及热应力进行分析,对比结果如图7所示。
在局部非热平衡模型下,岩石与循环工质的温差分布直接反映了热储层内发生热交换的范围,即开采区域。由图7可以看出,在距离注入井约0~60 m范围内液−岩温差为零,结合图3可知该区域岩石热能已被充分开采,岩石温度已达到工质的注入温度;在60~250 m范围存在液−岩温差,表明该区域为当前时刻热开采进行区域;在远离注入井250 m至生产井(距注入井约283 m)范围内,液−岩温差趋于零,工质已得到充分加热并与岩石达到温度平衡。值得注意的是,热储内岩石所受的热应力变化范围与液−岩温差曲线很好的吻合:在0~60 m区域热应力稳定于 −1.6 MPa左右,该区域热应力是由此时刻之前的热开采所形成,拉应力的最大值为 −1.62 MPa,其位置吻合于液−岩温差曲线中低温平衡区域与开采区域的交界位置(即距注入井约60 m位置);在60~250 m区域内,热应力幅值随着距注入井距离的增大而逐渐递减,而热应力变化曲线的拐点则吻合于液−岩温差曲线的峰值点;在远离注入井250 m的区域,热应力值趋于零。从物理角度而言,液−岩温差是触发工质与岩石热交换的动因,岩石在消耗热能的同时温度降低并产生体积收缩,从而产生拉应力。该拉应力随着岩石温度的降低而逐渐累积,液−岩温差最大位置则为当前时刻拉应力变化最显著的位置,当岩石温度降低至工质注入温度时,拉应力达到最大值。以上分析也说明了液−岩温差是造成热储内岩石热应力变化的根本动因。

图3 热储内岩石温度变化Fig. 3 Rock temperature distribution in the heat reservoir
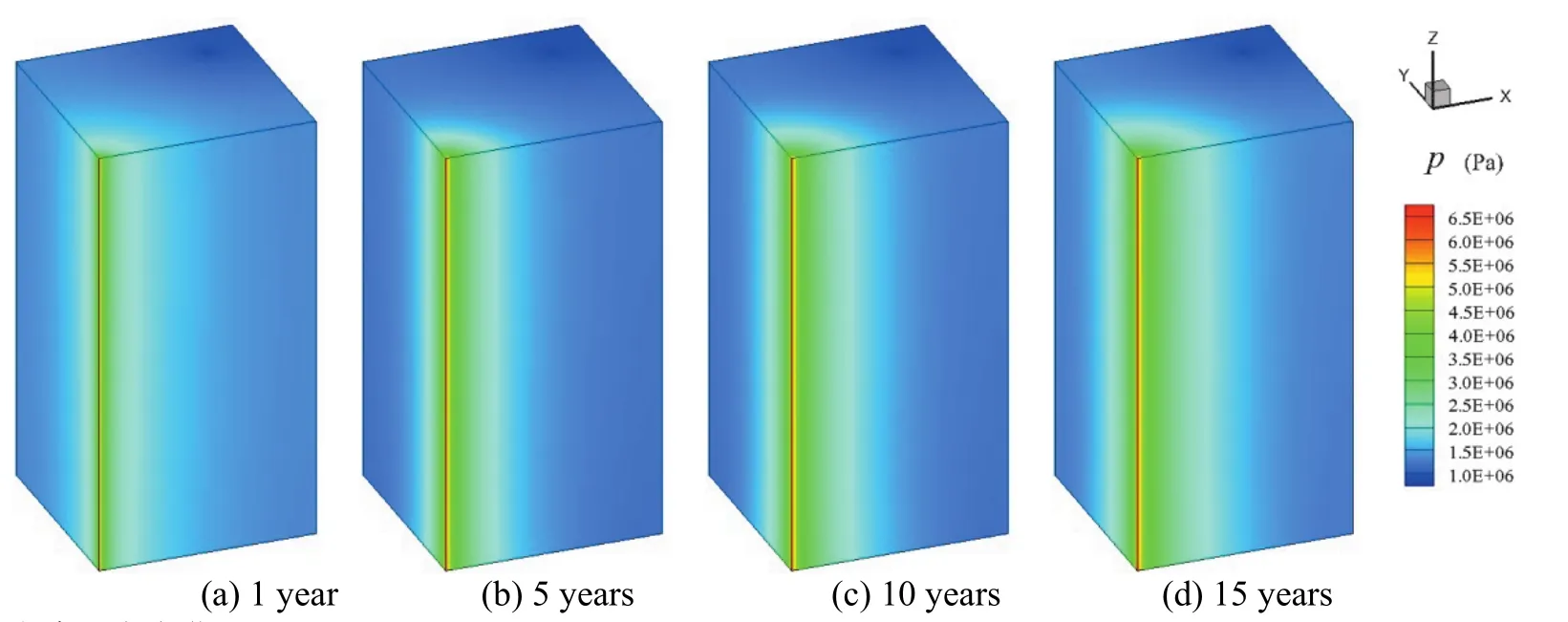
图4 热储内孔隙压力变化Fig. 4 Pore pressure distribution in the heat reservoir
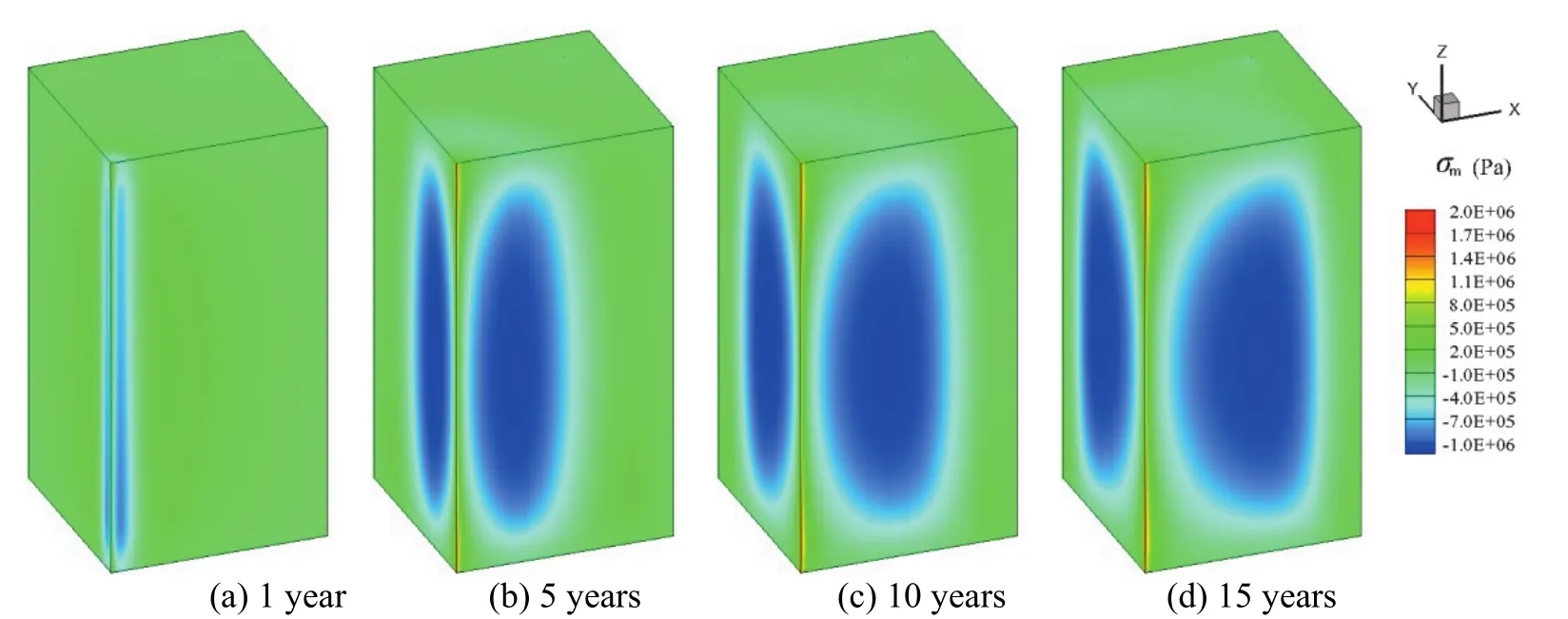
图5 岩石平均总应力变化Fig. 5 Mean total stress distribution in the heat reservoir

图6 开采至第5年时孔隙弹性应力及热弹性应力对比Fig. 6 Distribution of poro- and thermo- elastic stress at 5 years into the EGS operation

图7 液−岩温差与岩石热应力对比Fig. 7 The comparison between the liquid-rock temperature difference and the thermal stress in the reservoir
2.3 热开采过程应力场对采热性能的影响
由式(15)~式(17)计算获得的开采至第5年时热储有效应力、孔隙率及渗透率分布如图8所示。在注入井相邻区域,虽然平均总应力表现为最大压应力,但由于该位置孔隙压力也为最大值,因此该区域有效应力达到最大负值,对应的孔隙率及渗透率均达到最大值,表明该区域内裂隙开度在较大孔隙压力作用下产生增长。在距注入井较远范围内,孔隙率及渗透率同样大于初始值,该区域主要是因为岩石温度降低产生收缩,表明该区域为热应力作用区域。

图8 开采至第5年时有效应力、孔隙率、渗透率分布Fig. 8 Distributions of effective stress, porosity and permeability at 5 years
当孔隙率及渗透率发生改变时,热储内的渗流性能及换热性能均受到较大影响,从而使EGS采热性能发生显著变化。图9对比了有无应力场作用下出口井质量流量随时间的变化情况。可以看出,在采热的最初阶段,两种条件下出口井质量流量均表现为剧烈降低过程,这是因为注入井附近热储开始有低温工质流入,而工质在低温区域的粘度系数显著增大,使得注入井附近工质的动量损失相应增大。而在应力场作用条件下,出口井质量流量开始回升,由图8可知注入井相邻区域渗透率有所增大,降低了该区域的流动阻力。在后续运行中考虑应力场效应时出口井质量流率则在较高范围内变化(37 kg/s降低至30 kg/s),而不考虑应力场效应的质量流率低于20 kg/s。后续运行中质量流率的逐渐降低是因为热储内处于低温的流体逐渐增多,动量损失随着粘度系数的增大而增大。

图9 热储层内应力场对出口井质量流量的影响Fig. 9 Mechanical effects on the mass flow rate in EGS reservoir

图10 热储层内应力场对开采寿命及开采率的影响Fig. 10 Mechanical effects on the lifetime and the heat extraction ratio of the EGS
图10比较了有无应力场影响下的采出温度及采出热量随时间的变化情况,其中采出热量的描述由采热比(Heat Extraction ratio)给出:

式中,Tg为地表温度,Ts,ini为热储的初始温度,Vh为热储体积,Vb为基岩体积,Vh + Vb构成了图2所示的计算域体积。等式右端分母为以地表温度为参考的热储内总热能,分子包含了由热储内与基岩内已开采出的能量,该参数的实质是t时刻由EGS系统采出的无量纲化的总能量。可以看出,若以采出温度降低10 K作为系统废止的条件,即在本文中出口井采出温度降至450 K的时刻作为该系统的开采寿命,则在应力场影响下的开采寿命约为6.5年,低于不考虑应力场效应的开采寿命(12年)。在各自废止的时刻,应力场影响下的EGS热开采率约为0.25,不考虑应力场效应的热开采率约为0.26,略高于前者,这是因为开采寿命较长条件下周围岩石能够依靠热传导对已开采的低温区域进行热补偿,从而提高了热储的整体热开采率。以上结果表明应力场效应对EGS的采热性能具有显著影响,特别是注入井附近区域孔隙率渗透率的改变极大影响了后续热开采过程。
3 结 论
本文在基于局部非热平衡假设的EGS热开采过程三维计算模型基础上,根据热储层岩石中THM耦合的影响机理,考虑水的热物性随温度和压力的改变而变化的情况,从饱和多孔介质单相流体角度出发,建立了EGS热开采过程THM耦合的三维计算模型。对一理想的五口井EGS系统采热过程进行了THM计算,分析了岩石温度、孔隙压力对岩石应力场的作用机理,进一步研究了应力场对EGS采热性能的影响,主要结论如下:
(1)由孔隙压力造成的岩石应力为压应力,在距离注入井20 m范围内压应力高于1.0 MPa,由岩石温度变化引起的热应力为拉应力,随着热开采区域的扩展而扩展。
(2)液−岩温差是触发工质与岩石热交换的动因,同时也是产生热应力的根本。
(3)应力场效应对EGS的采热性能具有显著影响,特别是注入井附近区域孔隙率渗透率的改变极大影响了后续热开采过程。
[1] TESTER J W, ANDERSON B J, BATCHELOR A S, et al. The future of geothermal energy: impact of enhanced geothermal systems (EGS) on the United States in the 21st century[R]. America: Massachussets of Institute of Technology, 2006.
[2] KOH J, ROSHAN H, RAHMAN S S. A numerical study on the long term thermo-poroelastic effects of cold water injection into naturally fractured geothermal reservoirs[J]. Computers and Geotechnics, 2011, 38(5): 669-682.
[3] GHASSEMI A, ZHOU X. A three-dimensional thermo- poroelastic model for fracture response to injection/extraction in enhanced geothermal systems[J]. Geothermics, 2011, 40(1): 39-49.
[4] GHASSEMI A, TARASOVS S, CHENG A H D. A 3-D study of the effects of thermo-mechanical loads on fracture slip in enhanced geothermal reservoirs[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(8): 1132-1148.
[5] RAWAL C, GHASSEMI A. A reactive thermo-poroelastic analysis of water injection into an enhanced geothermal reservoir[J]. Geothermics, 2014, 50: 10-23.
[6] JEANNE P, RUTQVIST J, VASCO D, et al. A 3D hydrogeological and geomechanical model of an enhanced geothermal system at the Geysers, California[J]. Geothermics, 2014, 51: 240-252.
[7] MCDERMOTT C I, RANDRIAMANJATOSOA A R L, TENZER H, et al. Simulation of heat extraction from crystalline rocks: The influence of coupled processes on differential reservoir cooling[J]. Geothermics, 2006, 35(3): 321-344.
[8] JIANG F M, LUO L, CHEN J L. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems[J]. International Communications in Heat and Mass Transfer, 2013, 41: 57-62.
[9] JIANG F M, CHEN J L, HUANG W B, et al. A three-dimensional transient model for EGS subsurface thermo-hydraulic process[J]. Energy 2014, 72: 300-310.
[10] CHEN J L, JIANG F M. Designing multi-well layout for enhanced geothermal system to better exploit hot dry rock geothermal energy[J]. Renewable Energy, 2015, 74: 37-48.
[11] 陈继良, 罗良, 蒋方明. 热储周围岩石热补偿对增强型地热系统采热过程的影响[J]. 计算物理, 2013, 30(6): 862-870.
[12] 陈继良, 蒋方明, 罗良. 增强型地热系统地下渗流场的模拟和分析[J]. 计算物理, 2013, 30(6): 871-878.
[13] HU L T, WINTERFELD P H, FAKCHAROENPHOL P, et al. A novel fully-coupled flow and geomechanics model in enhanced geothermal reservoirs[J]. Journal of Petroleum Science and Engineering, 2013, 107: 1-11.
[14] The International Association for the Properties of Water and Steam. Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam[R]. Switzerland, 2007.
[15] The International Association for the Properties of Water and Steam. lamda Release on the IAPWS Formulation 2011 for the Thermal Conductivity of Ordinary Water Substance[R]. Czech Republic, 2011.
[16] The International Association for the Properties of Water and Steam. Viscosity Release on the IAPWS Formulation 2008 for the Viscosity of Ordinary Water Substance[R]. Germany, 2008.
[17] ARAIRO W, PRUNIER F, DJERAN M I, et al. On the use of effective stress in three-dimensional hydro- mechanical coupled model[J]. Computers and Geotechnics, 2014, 58: 56-68.
[18] NATHENSON M. The dependence of permeability on effective tress from flow tests at hot dry rock reservoirs at Rosemanowes (Cornwall) and Fenton Hill (New Mexico)[J]. Geothermics, 1999, 28: 315-340.
[19] RUTQVIST J, WU Y S, TSANG C F. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, anddeformation in fracturedporous rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 429-442.
The Thermal-Hydraulic-Mechanical Coupling Effects on Heat Extraction of Enhanced Geothermal Systems
CAO Wen-jiong, HUANG Wen-bo, JIANG Fang-ming
(Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China)
During heat extraction in enhanced geothermal systems (EGS), the reservoir porosity and permeability can be greatly affected by the multi-physical coupling of Thermal (T), Hydraulic (H), and Mechanical (M) actions. In the present work we develop a three-dimensional transient model coupling the subsurface THM behaviors during EGS heat extraction process. The local thermal non-equilibrium is assumed when describing the heat exchange between the rock matrix and heat transmission fluid. Case studies with respect to an imaginary quintuplet EGS reveal the involved mechanisms of inter-couplings in-between T-H-M actions, and the results indicate significant mechanical effects on EGS heat extraction performance. The stress of the rock matrix is largely influenced by the pore pressure and the temperature distributions. The stress triggered by fluid pressure is found to be compressive and confined in the very vicinity region of the injection well; the thermal stress is tensile and to some extent also concentrates around the injection well, but its distribution region expands toward the production well with the proceeding of heat extraction process. The temperature difference between rock matrix and heat transmission fluid is not only the driving force of heat extraction from heat reservoir but also significantly affects the formation of thermal stress in the reservoir.
enhanced geothermal system; local thermal non-equilibrium; THM coupling; variable properties
TK529
A
10.3969/j.issn.2095-560X.2015.06.006
2095-560X(2015)06-0444-08
曹文炅(1983-),男,博士,助理研究员,主要从事增强型地热系统的数值模拟及实验研究。
2015-09-18
2015-10-12
中科院百人计划(FJ);国家自然科学基金(51406213);NSFC-广东联合基金(U1401232);广东省自然科学基金重大基础培育项目(2014A030308001)
† 通信作者:蒋方明,E-mail:jiangfm@ms.giec.ac.cn
黄文博(1990-),男,博士研究生,主要从事增强型地热系统地下物理过程的数值模拟研究。
蒋方明(1973-),男,博士,研究员,博士生导师,中国科学院“百人计划”引进海外杰出人才。目前主要从事电化学能源/动力系统、增强型地热系统、微热流体系统、以及高效节能技术/产品等前沿科学和应用技术研究。
