基于一道中考填空题另解的收获
2015-06-01李玉荣金陵中学河西分校江苏南京210019
●李玉荣 (金陵中学河西分校 江苏南京 210019)
基于一道中考填空题另解的收获
●李玉荣 (金陵中学河西分校 江苏南京 210019)
《中学数学(初中版)》2014年第11期刊载了潘学军老师的文章“以问题为导向的个别答疑探究”.该文对一道几何题(2012年广东省深圳市数学中考题)的答疑实录十分详实,读来受益匪浅.同时,笔者也饶有兴趣地研究了此题的解法,得到一个更简单的实用解法,既开拓了学生的解题思路,也可以让学生跳出题海,体验波利亚在《怎样解题》中告诫的“你能在别的什么题目中利用这个结果或这种方法吗”,从而提高学生学习数学的效能.

图1

图2
题目 如图1,在Rt△ABC中,∠ACB=90°,AC=5,以AB为一边向外作正方形ABDE,联结AD,BE交于点,求BC的长.
解 如图2,将△OBC绕点O顺时针旋转90°得到△OAF,则
因为 ∠ACB+∠AOB=180°,
所以 ∠OAC+∠CBO=180°,
从而 ∠OAC+∠FAO=180°,
于是 BC=AF=12-5=7.
例1 1)如图3,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,联结EF,AG.求证:EF=FG.
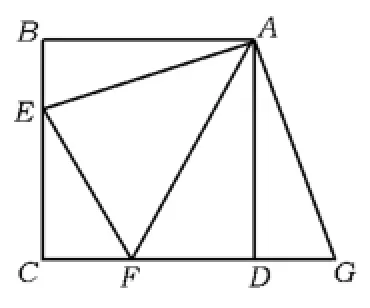
图3

图4
2)如图4,等腰 Rt△ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,求MN的长.
(2014年浙江省绍兴市数学中考试题)

图5
1)略;
2)解 如图5,将△ABM绕点A逆时针旋转90°得到△ACE,联结EN,则
BM=CE,AM=AE,
∠BAM=∠CAE,
∠ACE=∠ABC=45°,
从而 ∠NCE=∠ACB+∠ACE=90°,
于是 EN2=EC2+NC2.
又因为∠BAC=90°,∠MAN=45°,所以
∠BAM+∠CAN=45°.
于是 ∠EAN=∠MAN=45°.
在△MAN和△EAN中,由 AM=AE,∠MAN=
∠EAN,AN=AN,知
△MAN≌△EAN(SAS),
得MN=EN,
从而 MN2=BM2+NC2,
评注 这是由一道经典几何题改编的中考题,注意到∠BAC=90°,AB=AC,通过旋转可以将分散的条件集中在一个直角三角形中,问题得解.
例2 如图6,在四边形 ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为_______.
(2014年湖北省武汉市数学中考试题)
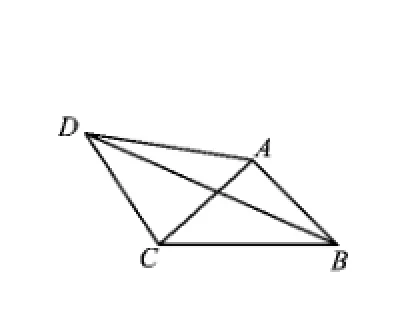
图6
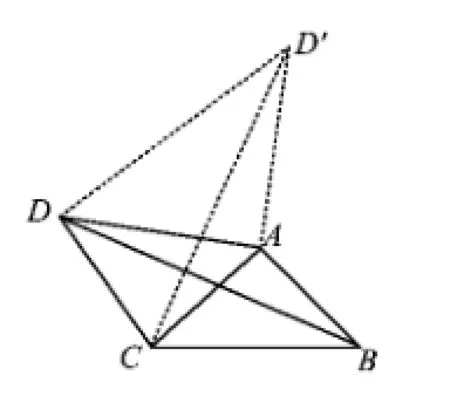
图7
解 如图7,将△ABD绕点A顺时针旋转90°得到△ACD',联结DD',则BD=CD',AD'=AD=4,∠DAD'=∠CAB=90°,从而
∠ADD'=45°,
评注 此题所求线段BD不在直角三角形中,无法直接求解,注意到∠BAC=90°,AB=AC,通过旋转可以将分散的条件集中在一个直角三角形中,问题得解.
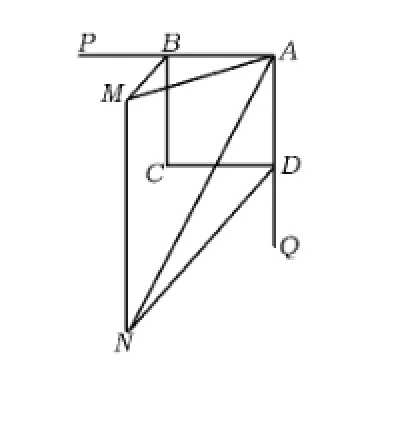
图8

图9
例3 已知:如图8,在正方形ABCD中,BM,DN分别平分正方形的2个外角,且满足∠MAN= 45°,联结MN.
1)若正方形的边长为a,求BM·DN的值;
2)若以BM,DN,MN为3条边围成三角形,试猜想三角形的形状,并证明你的结论.
(2014年山东省菏泽市数学中考试题)
1)略;
2)证明 以线段BM,DN和MN为3条边围成的三角形是直角三角形.下证明之.
如图9,将△AND绕点A顺时针旋转90°得到△ABF,联结MF,则∠1=∠3,AF=AN,BF=DN,∠AFB=∠AND,从而
∠MAF=∠1+∠2=∠2+∠3=∠BAD-∠MAN=45°,
于是 ∠MAF=∠MAN.
又因为 AM=AM,
所以 △AMF≌△AMN,
从而 MF=MN,
可得 ∠MBF=(∠AFB+∠1)+45°= (∠AND+∠3)+45°=90°.
因此在Rt△BMF中,BM2+BF2=FM2,从而 BM2+DN2=MN2,
于是以线段BM,DN和MN为3条边围成的三角形是直角三角形.
评注 猜想三角形的形状,需将线段BM,DN,MN“移植”到一个三角形中,注意到∠BAD=90°,AB=AD,通过旋转可以将分散的条件集中在一个直角三角形中,问题得解.
(2014年重庆市数学中考试题)
解 如图10,联结CG,易证

图10
△EBC≌△GDC(SAS),可得△ECG为等腰直角三角形.又CF⊥EG,得
CH=BH=GH.
将△HEB绕点 H逆时针旋转90°得到△HCM,又

由△GFH∽△GEA,得

评注 此题难度很大,如何使用条件BH=8是关键,在证明EH=CH后,通过旋转使分散的条件集中到一个直角三角形中,问题得解.
习题教学中,学生“做一题”,意在“会一类”,最终是“通一片”,也就是获得通法通解.通法通解是学生认知网络中不可缺少的一部分,它生成于学生知识的应用过程,对学生知识的迁移和能力的提升非常关键.解题不能只重结果——把思维仅仅停留在问题的解决上,要尽可能地引导学生悟出通性、通法,通过题目的变式、题组的甑选,将零散的问题恰当地组合,探究知识之间的联系,提炼、积累解题的方法,并努力寻求最佳的解法,使学生的数学思维能力在正迁移上得到新的发展.
从原问题的另解我们找到了一种方法——“旋转法”,再通过4道中考题解法的探究,旨在让学生知道利用图形的旋转是解决正方形(或等腰直角三角形)问题的通性、通法.旋转法就是在图形具有“公共端点的相等线段且其夹角为特殊角”的特征时,可以把图形或图形的一部分绕公共端点旋转到另一位置的一种辅助线的方法:1)旋转变换的实施条件——共端点(旋转中心)、等线段(确保移动一边能与另一边重合)、等线段共端点的2条边的夹角为特殊角(旋转角,一般为45°,60°,90°);2)旋转变换的实施对象——将已知的2条等线段分别所在的现有三角形(2条等线段所组成的三角形除外)、或将已知的2条线段分别与第3个顶点构成的三角形之中的一个三角形先进行旋转,并确保旋转前后的2个三角形中的已知等线段互相重合;3)旋转变换的实施功效——由于旋转前后的2个三角形重合、全等,这为边、角的等量代换转移位置提供了方法,同时为旋转、联结之后的全等证明提供了思路,最终为解决问题创造了一个关键条件.
综合性几何题的困难主要集中在2个方面:一是怎样作辅助线;二是怎样探索证题思路.而旋转变换的思想方法就能较好地解决这2个问题.旋转与之前的平移、轴对称相比,在发展学生空间想象能力、学生几何直观能力等方面具有独特的优势.此外,从教材到相应的教师教学用书,并没有真正体现出“旋转法”应有的功能,导致学生缺失从“旋转法”的视角去分析、思考几何综合题的意识.因此,帮助学生学会、学透“旋转法”,并能自觉地尝试优先从“旋转法”的视角去分析、思考几何综合题,进而提高解决几何综合题的能力,并在此基础上进一步夯实数学基础知识,应成为教师的自觉行动!
[1] 潘学军.以问题为导向的个别答疑探究[J].中国数学教育:初中版,2014(11):18-22.
[2] 李晓华.对图形旋转问题的探究与思考[J].中国数学教育:初中版,2010(9):23-24.
