三角代数的模糊滤子

罗敏霞，潘 琼

（中国计量学院 数学与信息科学系，浙江 杭州 310018）

模糊逻辑起源于Zadeh 1973年提出的模糊推理思想［1］.模糊逻辑是经典逻辑的一般化，模糊逻辑的命题演算系统中，公式不仅可以以0和1作为真值，也可以是在［0，1］上的值.ML逻辑是基于剩余格的逻辑系统［2］，它是诸多模糊逻辑的基础，如Esteva和Godo的基于左连续三角范数的MTL模糊逻辑系统［3］是 ML逻辑系统的扩张，Hajek的基于连续三角范数的基本逻辑BL系 统［4－5］是MTL逻辑系统的扩张，著名的Lukasiewicz逻辑、Godel逻辑及乘积逻辑都是BL逻辑的扩张.这些逻辑的语义代数模型分别是剩余格、MTL－代数、BL代数、MV代数、Godel代数和乘积代数［6］.Gasse等首先提出了三角代数的概念［7］，三角代数等价于区间值剩余格IVRLs，被用来构造三角逻辑TL系统，是三角逻辑的语义代数模型.

在模糊逻辑理论研究中，逻辑代数的滤子发挥着非常重要的作用.文献［3］给出了 MTL－代数中滤子的定义，利用滤子证明MTL逻辑系统的完备性；文［8－9］给出 MTL代数模糊滤子的定义和等价刻画.Hájek在文献［4］中给出BL－代数滤子的定义，并证明了BL逻辑系统的完备性.Gasse等在文献［7］中引入三角代数的滤子概念，并使用滤子证明三角逻辑系统的完备性.

本文在三角逻辑的基础上给出三角代数的模糊滤子的概念，并研究其性质，进一步给出三角代数中滤子与模糊滤子之间的关系，从而可以为更好地研究三角逻辑提供完善的逻辑语义模型.

1 预备知识

定义1.1［4，11］一个代数结构 L＝（L，∧，∨，⊗，→，0，1），如果满足下列条件：

1）L＝（L，⊗，1）是一个可换独异点；

2）L＝（L，∧，∨）是一个有界格；

3）x⊗y≤z⇔x≤y→z；

则称L＝（L，∧，∨，⊗，→，0，1）是一个剩余格.

命题 1.1［4］在一个剩余格中以下结论成立：

我们定义x＊＝∨｛y∈L｜x⊗y＝0｝等效于x＊＝x→0，以及

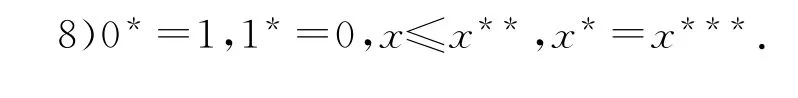
定义1.2［7］格L＝（L，∧，∨，⊗，→，ν，μ，0，u，1）称为三角代数，其中（L，∧，∨，⊗，→，0，1）是一个剩余格，ν，μ是一元运算符，u是一个常数，如果满足以下条件：

定义1.3［10］设格L＝（L，∧，∨，⊗，→，ν，μ，0，u，1）是三角代数，L中的一个元素x 被称为准，如果νx＝x，L的确切元素的集合记作E（L）.

定理1.2［7］在一个三角代数L＝（L，∧，∨，⊗，→，ν，μ，0，u，1）中，蕴含→和⊗完全由E（L）上的作用和μ（u⊗u）的值来定义，具体为：

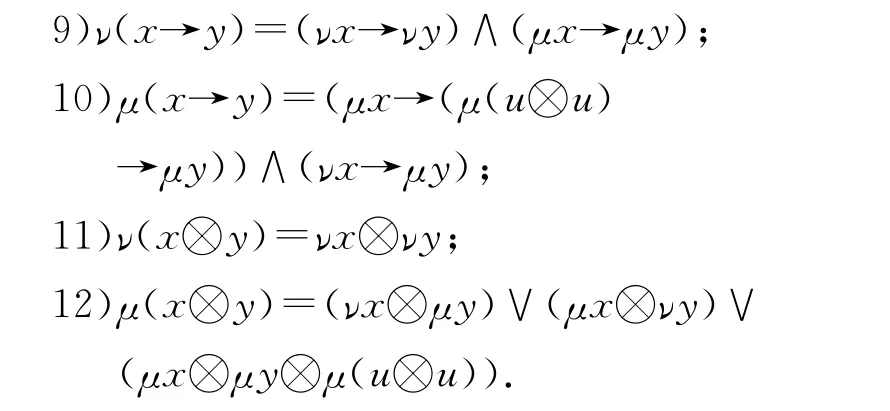
定义1.4［10］设L＝（L，∧，∨，⊗，→，ν，μ，0，u，1）是一个三角代数，L的一个非空子集F称为L的一个滤子，如果满足

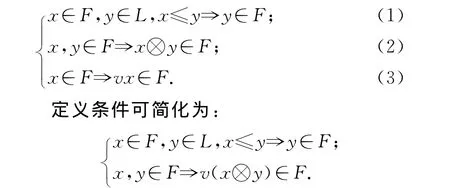
命题1.3 设L＝（L，∧，∨，⊗，→，ν，μ，0，u，1）是一个三角代数，F是L的一个非空子集，则F是L的滤子当且仅当

证明：设F是满足（4）和（5）的L的非空子集，设x，y∈L，使得x≤y且x∈F，通过（4）可得到x→y＝1∈F，由（5）得到y∈F，所以（1）是成立的.设x，y∈F，则x→（y→（x⊗y））＝（x⊗y）→（x⊗y）＝1∈F，从（5）中隐含表明x⊗y∈F，因此（2）成立；设x，y∈F，有ν（x⊗y）＝νx⊗νy∈F，则由x→（y→x）＝1得νx→（νy→νx）＝（νx⊗νy）→νx＝1∈F.由（5）得νx∈F，因此（3）成立.

反之，假设F是L的一个滤子，显然由（1）得1∈F，设x，y∈L使得x∈F并且x→y∈F，由（2）得x⊗（x→y）∈F，利用y≤（y→x）→x有x≤（x→y）→y，即x→（（x→y）→y）＝1＝（x⊗（x→y））→y＝1，即（x⊗（x→y））≤y，由（1），因此（5）成立；由（2）和（3）显然（6）成立.

2 模糊滤子与滤子的关系

定义2.1 设L是一个三角代数，L中的一个模糊集w称为L的一个模糊滤子，如果它满足条件：

例1 设L＝［0，1］，定义运算⊗与→如下：

对所有的x，y∈L，则L就是三角代数.

根据三角代数的模糊滤子的定义，进一步研究模糊滤子的等价刻画.

定理2.1 设w是三角代数L的一个模糊集，则w是L的一个模糊滤子当且仅当

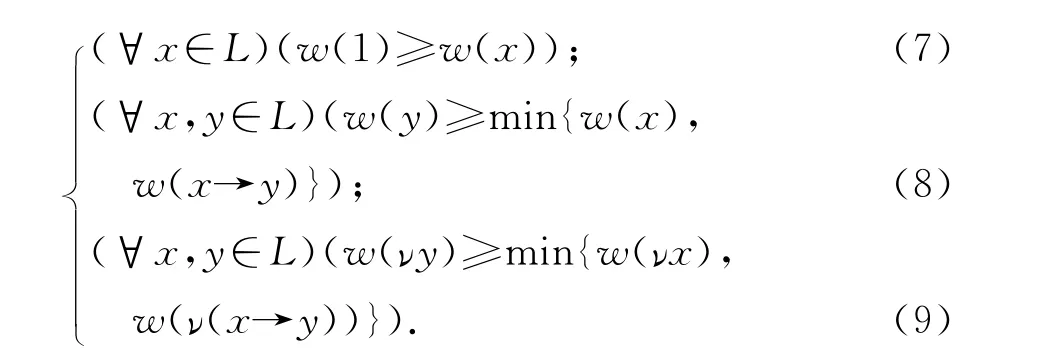
证明：假设w 满足条件（7）和（8），设x，y∈L使得x≤y，则x→y＝1，所以由条件（7）和（8）得到w（y）≥min｛w（x），w（1）｝＝w（x），因此（c2）是成立的.利用命题1.1的（1），可知x→（y→（x⊗y））＝（x⊗y）→（x⊗y）＝1，于是根据条件（7）和（8）我们有

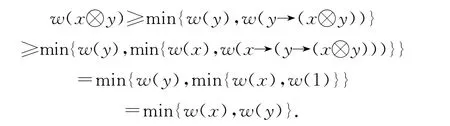
因此（c1）是成立的.根据条件（7）和（9）可得：

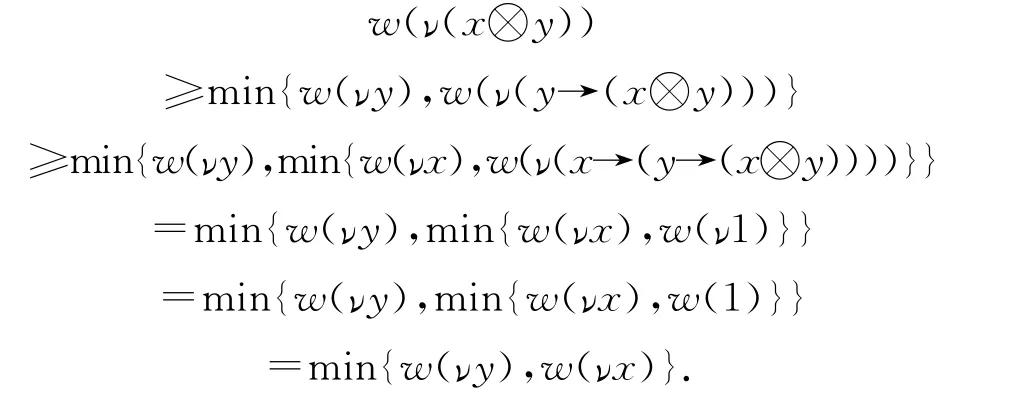
即（c3）是成立的.假设w是L的一个模糊滤子，当对所有的x∈L，x≤1，则由（c2）得到对所有的x∈L有w（1）≥w（x）.由定义1.2的（8）以及伽罗佤对应我们可知ν（x→y）≤νx→νy⇔ν（x→y）⊗νx≤νy，因此由（c2）和（c3）可得 w（νy）≥w（νx⊗ν（x→y））≥min｛w（νx），w（ν（x→y））｝，证毕.

进一步研究三角代数中滤子与模糊滤子之间的关系，证明三角代数中模糊滤子与滤子的相互诱导.

定理2.2 设F是三角代数L的一个滤子，且a∈L，w是L的一个模糊集

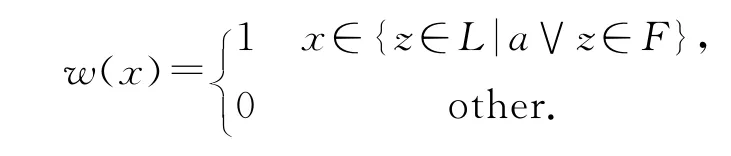
则w是L的一个模糊滤子.

证明：已知a∨1∈F，我们有1∈｛z∈L｜a∨z∈F｝和对所有x∈L得到w（1）＝1≥w（x），现在如果y∈｛z∈L｜a∨z∈F｝，那么可以清楚地得到w（y）＝1≥min｛w（x），w（x→y）｝.假设y∉｛z∈L｜a∨z∈F｝，那么存在x和x→y至少其中一个不属于｛z∈L｜a∨z∈F｝，于是w（y）＝min｛w（x），w（x→y）｝.同样如果νy∈｛z∈L｜a∨z∈F｝则可清楚地得到w（νy）＝1≥min｛w（νx），w（ν（x→y））｝，假设νy∉｛z∈L｜a∨z∈F｝，那么存在νx和ν（x→y）至少其中一个不属于｛z∈L｜a∨z∈F｝，于是w（νy）＝min｛w（νx），w（ν（x→y））｝，因此w是L的一个模糊滤子.

定理2.3 如果w是L的一个模糊滤子，那么对于每一个a∈L，集合Ωa＝｛x∈L｜w（x）≥w（a）｝是L的一个滤子.

证明：已知对所有x∈L有w（1）≥w（x），我们有1∈Ωa，设x，y∈L使得νx∈Ωa和ν（x→y）∈Ωa，那么就有w（νx）≥w（a）和w（ν（x→y））≥w（a）.已知w是L 的一个模糊滤子，从（8）可得w（νy）≥min｛w（νx），w（ν（x→y））｝≥w（a）；又因为w（y）≥w（νy），w（x→y）≥w（ν（x→y）），所以（x→y）∈Ωa，w（y）≥w（a）以及 w（ν（x⊗y））≥min｛w（νx），w（νy）｝≥w（a），所以y∈Ωa且ν（x⊗y）∈Ωa，因此Ωa是L的一个滤子.

3 结 语

本文在三角代数滤子定义的基础上给出了滤子的等价刻画，进一步引入三角代数中模糊滤子的概念，给出模糊滤子的等价刻画.特别研究三角代数中模糊滤子与滤子之间的关系，证明了模糊滤子与滤子可相互诱导.

［1］ZADEH L A.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems，Man Cybernetics，1973，3（1）：28－44.

［2］HOHLE U.Monoidal logic［C］／／Fuzzy systems in computer science.Germany：Vieweg＋ Teubner Verlag，1994：233－243.

［3］ESTEVA F，GODO L.Monoidal t－norm based logic：towards a logic for left－continuous t－norms［J］.Fuzzy Sets and Systems，2001，124（3）：271－288.

［4］HAJEK P.Metamathematics of Fuzzy Logic［M］.Dordrecht：Kluwer Academic Publishers，1998：29－48.

［5］HAJEK P.Basic fuzzy logic and BL－algebras［J］.Soft Computing，1998，2（3）：124－128.

［6］FONT J，RODR GUEZ A J，T ORRENS A.Wajsberg algebra［J］.Stochastica，1984，8（1）：5－31.

［7］GASSE B V，COMELIS C，DESCHRIJVER G，et al.Triangle algebras：A formal logic approach to interval－valued residuated lattices［J］.Fuzzy Sets and Systems，2008，159：1042－1060.

［8］JUN Y B，XU Y，ZHANG X H.Fuzzy filters of MTL－algebras［J］.Information Sciences，2005，175：120－138.

［9］KIM K H，ZHANG Q，JUN Y B.On fuzzy filters of MTL－algebras［J］.Journal of Fuzzy Mathematics，2002，10（4）：981－989.

［10］GASSE B V，COMELIS C，DESCHRIJVER G，et al.The pseudo－linear semantics of interval－valued fuzzy logics［J］.Information Sciences，2009，179：717－728.

［11］TURUNEN E.BL－algebras of basic fuzzy logic［J］.Mathware and Soft Computing，1999，6（1）：49－61.