基于自由处置性的网络系统效率评价模型研究

周忠宝，喻怀宁，马超群，刘 佩，刘文斌,2

(1. 湖南大学工商管理学院，长沙 410082； 2. Business School, University of Kent, Kent, CT2 7PE)

基于自由处置性的网络系统效率评价模型研究

周忠宝1，喻怀宁1，马超群1，刘 佩1，刘文斌1,2

(1. 湖南大学工商管理学院，长沙 410082； 2. Business School, University of Kent, Kent, CT2 7PE)

网络系统生产可能集是构建网络DEA模型的基础，而相邻生产子过程的投入产出连接条件则是构造生产可能集的关键。现有的网络DEA模型在本质上都假设所有子过程的投入产出都满足强自由处置性，然而在实际生产管理活动中，这一假设未必成立。本文从各类自由处置公理出发，系统地研究了各种类型的子过程投入产出连接条件，构建了一般网络系统的生产可能集，给出了相应的等价形式，并构建了相应的网络DEA模型用于评价决策单元的效率。最后利用本文提出的方法和模型对我国上市银行的效率进行了评价。本文的研究对于一般网络系统的绩效评价和改进具有重要的意义。

网络系统；自由处置性；生产可能集；数据包络分析；效率评价

1 引言

数据包络分析方法(Data Envelopment Analysis，DEA)是著名运筹学家Charnes, Cooper和Rhodes于1978年提出的基于投入产出分析的非参数绩效评价方法。由于DEA模型的非参数特征，应用时只需对生产函数或生产前沿面做一些合理的定性假设，而无需指定具体的生产函数形式，因而能有效地避免模型设定误差。同时DEA模型能够处理多输入多输出数据，评估结果都是基于观测数据的，无需事先设定权重，因而有效地避免了评价的主观性。该方法已成功应用于银行、工厂、医院、学校等多种社会经济组织的效率评价。

传统的CCR、BCC等模型将每个决策单元(Decision Making Unit, DMU)视为黑箱系统，从整体层面研究被评价对象的效率，而没有深入探究内部结构特征对决策单元效率的影响。在实际问题中，决策单元(系统)往往是由很多结构复杂的内部子系统组成的，一个子系统的投入往往是其它子系统的部分或全部产出，各个不同功能的子系统组成串联结构、并联结构，或者由串联和并联组成的复杂网络结构。例如，仅由供应商-零售商构成的一个简单供应链系统就是典型的具有串联结构的决策单元，商业银行则可以视为由多个分行组成的并联系统。传统的DEA模型不考虑系统内部结构，因而可能会高估系统层次的投入-产出效率[20]。为了解决这一问题，很多学者提出了考虑系统内部结构的网络DEA(Network DEA,NDEA)模型。对于串联系统，Liang Liang等[11]从博弈论的角度出发构建了Centralized 模型和Leader-Follower模型，将系统效率分解为子系统效率的乘积。Kao 等[8]构建了与Centralized模型等价的Relational 模型并将其应用于评价台湾非寿险公司的效率。Yang Feng等[15]和Zhou Zhongbao等[17]讨论了两阶段供应链系统的生产可能集及其等价形式。毕功兵等[18]提出了一种资源约束型两阶段生产系统的DEA效率评价模型，并研究其内部运行机制对整体效率的影响。对于并联系统，Yang Feng等[16]提出了一个YMK模型用于评价并行系统的效率，但该模型仅适用于子系统完全独立的情形。杨锋等[19]分析了并联生产系统的前沿生产能力, 提出了评价并联生产系统的乘子模型和包络模型。Kao等[7]将系统的非有效性测度分解为子系统的加权平均，并将其应用于台湾林业管理效率评价。对于一般的网络系统，Färe等[5]从网络系统的生产可能集出发，构建了FG网络模型，提出采用方向距离函数度量网络系统的效率，并给出了Malmquist指数的计算方法。Prieto等[13]利用上述FG网络模型对OECD国家的投入产出进行了分析。Lewis等[10]考虑了网络生产过程的前沿生产能力，提出了计算网络系统和子系统效率的LS网络模型，并将其用于美国职业棒球大联盟的效率评价。Kao等[6,9]通过引入隐过程，将整个网络分解为一个串联系统，其中的子系统具有相同的并联子过程，进而在Relational模型的基础上，将系统效率分解为串联子系统效率的乘积，每个子系统的Slacks分解为所包含的子过程的Slacks之和，并将该模型用于评价台湾非寿险公司的效率。Castelli等[1-2]对具有分层结构的网络系统效率评价问题进行了研究，提出了两个DEA-Like模型，其区别在于对不同层次子系统的关联约束的假设。Chang等[3]考虑了网络系统的所有制结构，提出了三种网络DEA模型：Centralized模型、Distributed模型和Hybrid模型。

与传统的DEA模型相比，这些模型能够较为合理地评估决策单元的效率，然而这些模型在本质上都假设每个子生产过程的投入产出都满足强自由处置性，即更多的投入可以生产更少的产出。然而在实际生产经营活动中，这一假设未必成立。如在评价火力发电站环境效率时，SO2等污染物的排放则满足弱自由处置性假设，即期望产出和非期望产出需要按同样的比例减少。本文基于不同的自由处置性假设，系统地研究了网络系统中相邻子生产过程的投入产出连接条件，构建了一般网络系统的生产可能集及其等价形式，进而建立了相应的网络DEA模型用于评价网络系统的效率，最后将其应用于商业银行效率评价问题。

2 基于自由处置性的网络系统生产可能集及DEA模型

假设共有n个决策单元，每个决策单元具有相同的网络结构，如图1所示。网络中的每一个节点代表一个子生产过程。网络中所有的节点可以分为三类：不存在紧前节点的节点，不存在紧后节点的节点，既有紧前节点又有紧后节点的节点，其对应的集合分别记为S、T和M。

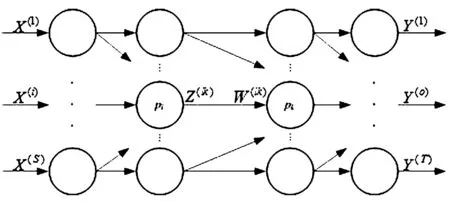
图1 网络系统示意图

集合S中的子生产过程pi的输入向量记为X(i)，i∈S；集合T中的子生产过程po的输出向量记为Y(o)，o∈T；集合T和M中子过程pk的紧前节点集合记为Pk，k∈M∪T;集合S和M中的子过程pl的紧后节点集合记为Dl，l∈M∪S。

2.1 规模收益不变假设下的生产可能集及DEA模型

本文沿用Färe[5]提出的基于生产可能集来构建网络DEA模型的思路，此方法在Chen Ci[4]中得到了进一步的发展。结合Liu W B等[12]的思路，根据每个子生产过程投入产出的自由处置性假设，首先构建相应的生产可能集，进而基于生产可能集构建相应的网络DEA模型。

假设网络系统中的所有子过程的规模收益不变，以下讨论几种典型的生产可能集及DEA模型，对于其他更加复杂的情况可以得到类似地讨论。

(1)假设所有节点的输入输出均满足强自由处置性(如常见的供应商-零售商供应链系统)，则生产可能集可表示为：

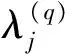
容易证明上述生产可能集等价于：

(1)

对应的输入径向模型可表示为：

minθ

(2)

(2)假设所有节点的输入满足强自由处置性，输出满足弱自由处置性(如同时考虑期望产出发电量和不期望产出二氧化硫的多个火力发电机组构成的并联系统，此时可以认为输入满足强自由处置性，输出满足弱强自由处置性)，则生产可能集可表示为：

上述生产可能集等价于：

(3)

对应的输入径向模型可表示为：

minθ

(4)

(3)假设所有节点的输入满足弱自由处置性，输出满足强自由处置性(如以化肥厂作为单元构成的并联生产系统，原材料必须按照同样的比例增加，化肥产量才能保证不会降低，否则可能会引起化肥产量降低，此时可以认为输入满足弱自由处置性，输出满足强自由处置性)，则生产可能集可表示为：

上述生产可能集等价于：

(5)

对应的输入径向模型可表示为：

minθ

(6)

(4)假设所有节点的输入输出均满足弱自由处置性(如在上述化肥厂例子中，若同时考虑污染物排放量这一不期望产出，则可以认为输入输出都满足弱自由处置性)，则生产可能集可表示为：

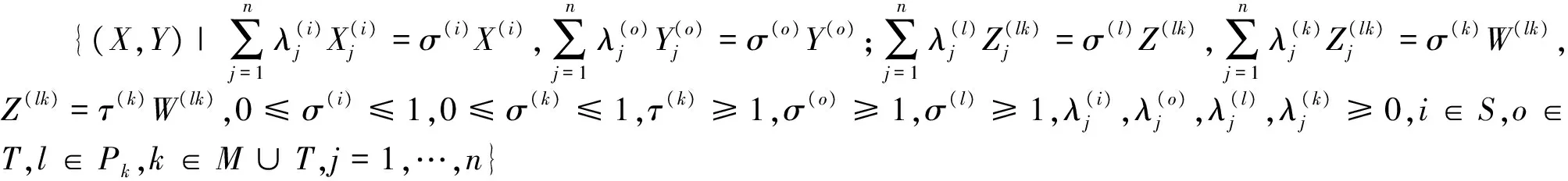
(7)

对应的输入径向模型可表示为：

minθ

(8)

(5)假设所有的初始输入和最终产出满足强自由处置性，中间的投入产出不能自由处置(如N个阶段基金绩效评价中，基金在每个阶段的收益率不能自由处置，必须完全传递给下一阶段)，则生产可能集可表示为：

上述生产可能集等价于：

(9)

对应的输入径向模型可表示为：

minθ

(10)

2.2 规模收益可变假设下的生产可能集及DEA模型

假设网络系统中的所有子过程的规模收益可变，以下讨论几种典型的生产可能集及DEA模型，对于其他更加复杂的情况可以得到类似的结论。

(1)假设所有节点的输入输出均满足强自由处置性，则生产可能集可表示为：

上述生产可能集等价于：

(11)

对应的输入径向模型可表示为：

minθ

(12)

(2)假设所有节点的输入满足强自由处置性，输出满足弱自由处置性，则生产可能集可表示为：

(13)

对应的输入径向模型可表示为：

minθ

(14)

(3)假设所有节点的输入满足弱自由处置性，输出满足强自由处置性，则生产可能集可表示为：

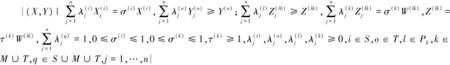
(15)

该情形下的输入径向模型为非线性规划，而输出径向模型则可表示为如下的线性规划：

minφ

(16)

(4)假设所有节点的输入输出均满足弱自由处置性，则生产可能集可表示为：

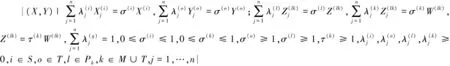
(17)

对应的输入径向模型可表示为：

minθ

(18)

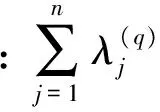
限于篇幅，上面仅仅讨论了所有子过程规模收益不变或所有子过程规模收益可变两种情形下的生产可能集及DEA模型，实际中还存在部分输入(输出)满足强自由处置性，另一部分输入(输出)满足弱自由处置性，以及部分子生产过程规模收益不变，另一部分子生产过程规模收益可变的情况。此时可以根据本文提出的思路和方法，构建相应的生产可能集和DEA模型。

3 商业银行效率评价

商业银行效率的评价是DEA应用的一个重要领域，本文选取员工人数、固定资产和营业费用作为第一阶段的投入，贷款总额和优良贷款额为第一阶段的产出，同时也是第二阶段的投入，第二阶段的产出包括净利润和市场价值。所评价的2011年16家上市银行的投入产出数据如表1所示，数据来源于中国金融统计年鉴(2011)，上市银行年报(2011)以及国泰安数据库。

对于第一阶段的投入X和第二阶段的产出Y，显然应假设其符合强自由处置性。而对于贷款总额和优良贷款额，两者作为第一阶段的相伴产出，是不可分离的，而且对特定的银行而言，两者的比率可以认为保持不变(即优良贷款率)，因而可以假设两者作为第一阶段的产出满足弱自由处置假设。而两者作为第二阶段的投入，显然应该假设其满足强自由处置性。因而可以构建如下的生产可能集：

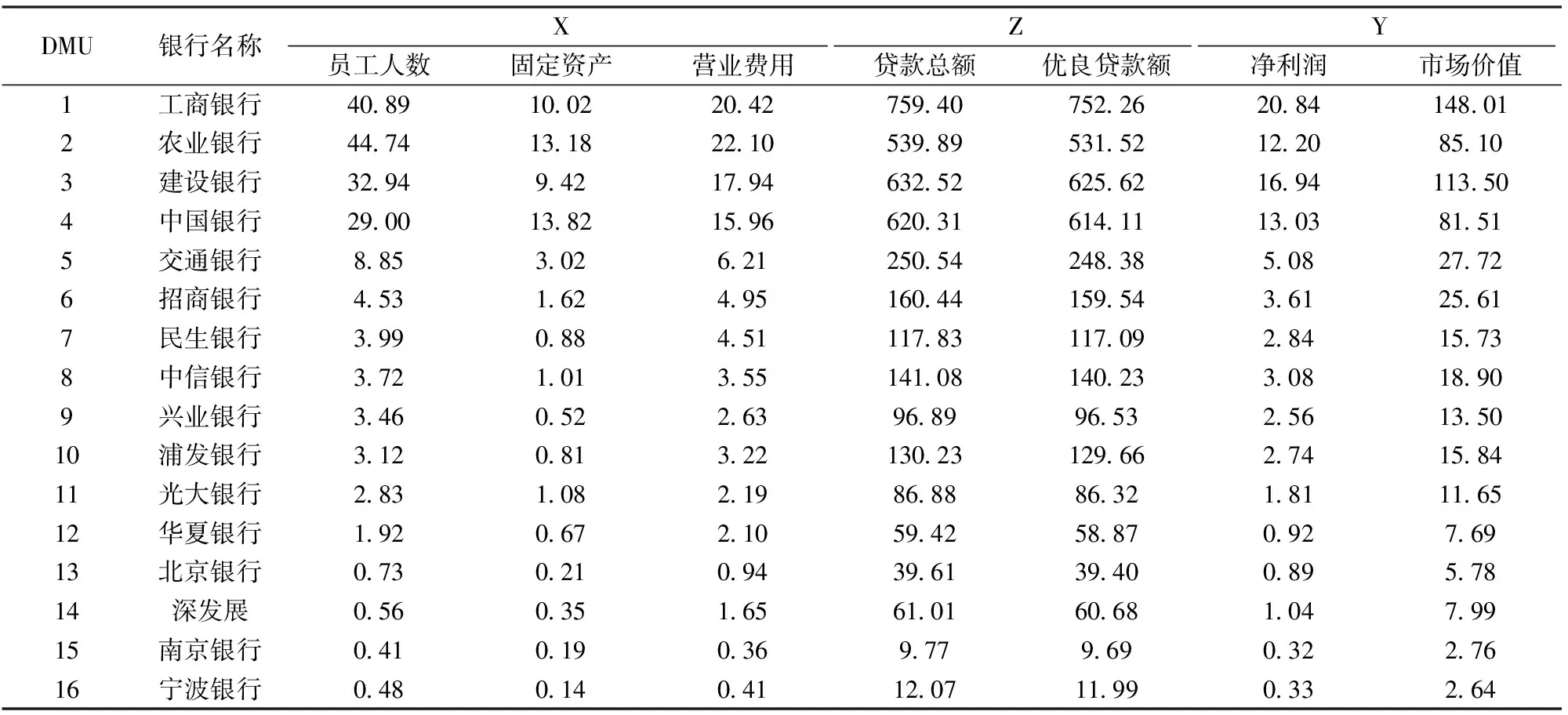
表1 我国16家上市银行2011年投入产出数据

(19)

上述生产可能集等价于：

(20)

对应的输入径向模型可表示为：

minθ

(21)

minθ

(22)

我们首先采用BCC模型计算了总系统和各阶段的效率，为了与网络模型保持一致，在计算总系统BCC效率时，假设输入和输出都满足强自由处置性；在计算第一阶段BCC效率时假设输入满足强自由处置性，输出满足弱自由处置性；在计算第二阶段BCC效率时，假设输入和输出都满足强自由处置性。然后分别采用不考虑中间产品自由处置性和考虑中间产品自由处置性的网络DEA模型(22)计算了总系统的效率，并采用其对偶(乘子)模型计算各个阶段的效率。计算结果比较如表2所示。

对于总系统的BCC效率和考虑自由处置性的NDEA效率，采用Wilcoxon秩和检验结果表明，在5%的置信水平下，两个模型的计算结果存在显著性差异。通过表2可以看出， 部分银行的效率及排名变化比较大，如DMU6，BCC效率为1.000，排名第1，而NDEA效率仅为0.686，排名第13，差别非常大。同样的情况还存在于DMU10、DMU8。此外，对于DMU6、DMU8、DMU9、DMU10、DMU13、DMU14，在系统层次是BCC有效的，然而各子系统的效率表明，第二阶段均为BCC非有效，这是由于BCC模型把系统作为一个黑箱来处理，网络模型则考虑了系统内部网络结构，因而评价结果更加合理。对于这些决策单元，BCC模型均判定其有效，无法区分其系统层次的绩效水平，而采用考虑自由处置性的NDEA模型则可以有效地进行区分。这是由于考虑系统内部网络结构后所构造的生产可能集包含BCC模型对应的生产可能集，从而导致相应的生产前沿面上移，因而提高了模型的分辨率。

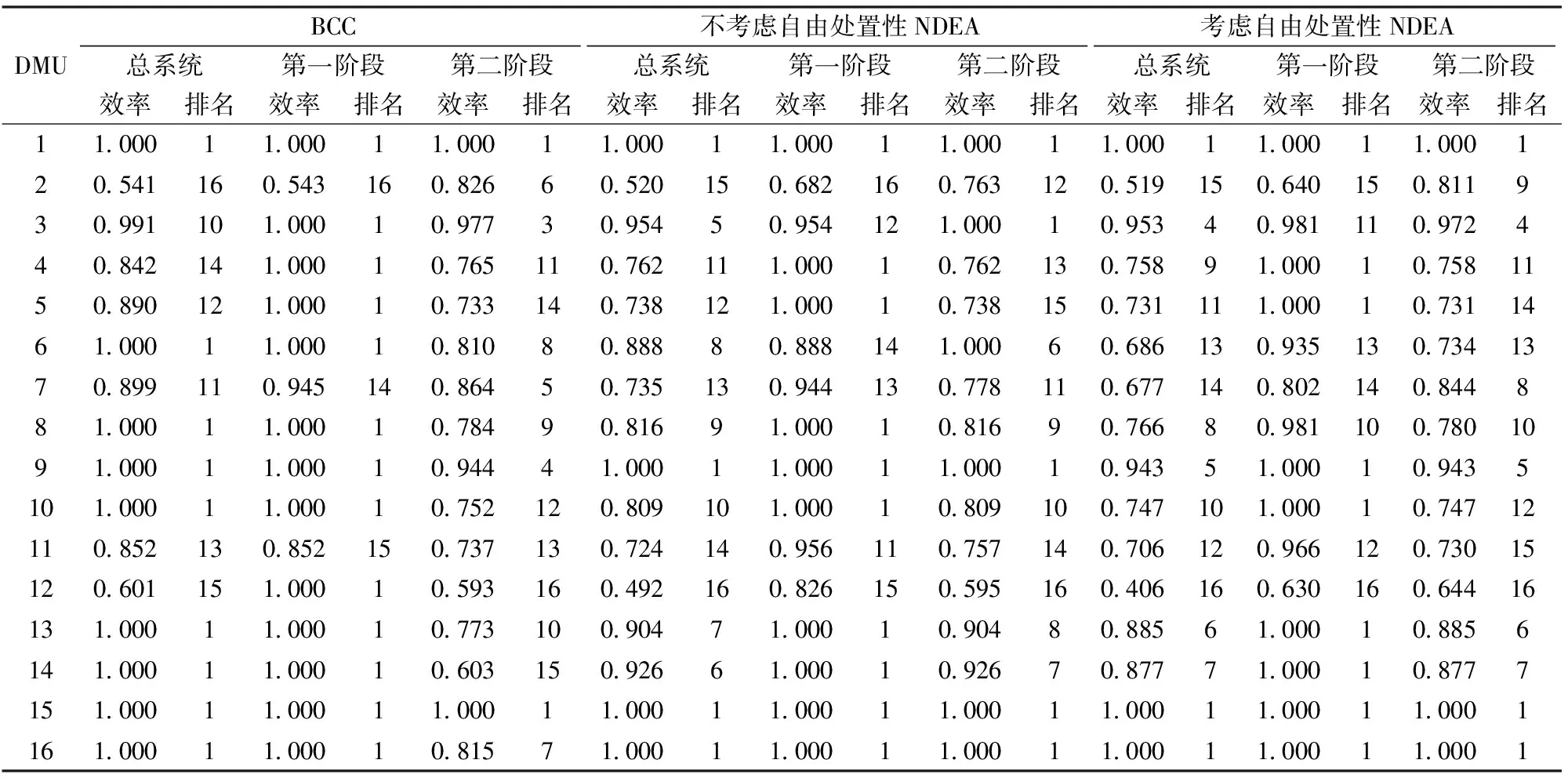
表2 我国16家上市银行效率及排名比较

对于不考虑自由处置性的NDEA效率和考虑自由处置性的NDEA效率，通过表2可以看出，对于DMU8而言，在不考虑自由处置性时，第一阶段是有效的，而考虑自由处置性时，第一阶段则为非有效的。由此可见，考虑自由处置性对于发现导致系统非有效的原因有重要意义。此外，不考虑自由处置性的NDEA效率均大于或者等于考虑自由处置性的NDEA效率，在不考虑中间产品的自由处置性时，DMU9是有效的决策单元，而考虑中间产品的自由处置性时，DMU9则是非有效的。这是因为后者对应的生产可能集包含前者所对应的生产可能集，从而导致相应的生产前沿面上移。由此可见，考虑网络各节点投入产出的自由处置性对于提高模型的分辨率、发现系统的薄弱环节具有重要的意义。

此外，通过表2可以看出，在网络DEA模型中，总系统的效率可以分解为两个阶段效率的乘积。对于非有效的决策单元DMU4、DMU5、DMU9、DMU10、DMU13、DMU14，可以发现导致这些决策单元非有效的都是第二阶段，这是因为网络模型考虑了系统内部网络结构，可以为系统绩效提升提供重要的参考。

4 结语

网络系统效率评价是目前研究的热点问题，生产可能集是构建网络DEA模型的基础，而各网络节点的投入产出连接条件则是构造生产可能集的关键。然而现有的研究假设所有子生产过程的投入产出都满足强自由处置性假设，然而由于实际生产管理的复杂性，这一假设并不总能满足。本文从各类自由处置公理出发，系统地研究了各种类型的子过程投入产出连接条件，构建了一般网络系统的生产可能集，给出了相应的等价形式，进而构建了相应的DEA模型用于评价网络系统的效率。最后通过对我国上市银行效率的评价，展示了本文提出的方法和模型的合理性与优越性。本文提出的生产可能集和DEA模型具有很强的适用性和可扩展性，所采用的思路、方法和模型可用于解决更为复杂的网络系统的效率评价问题。

[1] Castelli L, Pesenti R, Ukovich W. DEA-like models for efficiency evaluations of specialized and interdependent units[J]. European Journal of Operational Research, 2001,132(2): 274-286.

[2] Castelli L, Pesenti R, Ukovich W. DEA-like models for the efficiency evaluation of hierarchically structured units[J]. European Journal of Operational Research，2004， 154(2): 465-476.

[3] Chang T -S, Tone K, Wei Quanling. Ownership-specified network DEA models[J]. Annals of Operations Research,214(1): 1-26.

[4] Chen C, Yan Hong. Network DEA model for supply chain performance evaluation[J]. European Journal of Operational Research,2011, 213(1): 147-155.

[5] Färe R, Grosskopf S. Network DEA[J]. Socio-Economic Planning Sciences,2000, 34(1): 35-49.

[6] Kao C. Efficiency decomposition in network data envelopment analysis: A relational model[J]. European Journal of Operational Research,2009, 192(3): 949-962.

[7] Kao C. Efficiency decomposition for parallel production systems[J]. Journal of operation Research Society,2012, 63(1): 64-71.

[8] Kao C, Hwang S N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan[J]. European Journal of Operational Research,2008, 185(1): 418-429.

[9] Kao C, Hwang S N. Efficiency measurement for network systems: IT impact on firm performance[J]. Decision Support Systems,2010, 48(3): 437-446.

[10] Lewis H F, Sexton T R. Network DEA: Efficiency analysis of organizations with complex internal structure[J]. Computers & Operations Research,2004, 31(9): 1365-1410.

[11] Liang Liang, F. Yang Feng, Zhu J, et al. DEA models for supply chain efficiency evaluation[J]. Annals of Operations Research, 2006,145(1): 35-49.

[12] Liu W B, Meng W, Li X X, et al. DEA models with undesirable inputs and outputs[J]. Annals of Operations Research,2010, 173(1): 177-194.

[13] Prieto A M, Zofío J L. Network DEA efficiency in input-output models: With an application to OECD countries[J]. European Journal of Operational Research,2007, 178(1): 292-304.

[14] Tone K, Tsutsui M. Network DEA: A slack-based measure approach[J]. European Journal of Operational Research,2004, 197 (1): 243-252.

[15] Yang Feng, Wu Dexiang, Liang Liang, et al. Supply chain DEA: production possibility set and performance evaluation model[J]. Annals of Operations Research,2011, 185(1): 195-211.

[16] Yang Yinsheng, Ma Benjiang, Koike M. Efficiency-measuring DEA model for production system with k independent subsystems[J]. Journal of the Operations Research Society of Japan,2000, 43(3): 343-354.

[17] Zhou Zhongbao, Wang Mei, Ding Hui, et al. Further study of production possibility set and performance evaluation model in supply chain DEA[J]. Annals of Operations Research,2013, 206(1): 585-592.

[18] 毕功兵, 梁樑, 杨锋. 资源约束型两阶段生产系统的DEA效率评价模型[J]. 中国管理科学，2009， 17(2): 71-75.

[19] 杨锋, 梁樑, 凌六一，等 并联结构决策单元的DEA效率评价研究[J]. 中国管理科学，2009， 17(6): 157-162.

[20] 杨锋. 含有多个子系统的决策单元的DEA效率评估研究[D]. 合肥:中国科技大学，2006.

Research on Efficiency Evaluation Models for Network Systems Based on Free Disposability Principles

ZHOU Zhong-bao1，YU Huai-ning1，MA Chao-qun1，LIU Pei1，LIU Wen-bin1，2

(1. School of Business Administration, Hunan University, Changsha 410082, China;2. Business School, University of Kent, Kent, CT2 7PE, England)

Production possibility set (PPS) is the basis for constructing DEA models of network systems. The connection conditions of sub-processes are the key points for building the PPS. In nature, the existing network DEA models assume that all inputs and outputs of sub-processes satisfy the strongly free disposability principle. However, it is not always true in real production and management activities. Therefore, from the perspective of different free disposability principles, the connection conditions for inputs and outputs of sub-processes are studied; the production possibility sets and their equivalent formulations for general network systems are built. The DEA models are constructed accordingly for evaluating the efficiencies of network systems are built. In the end, the proposed models are used to evaluate the performance of China′s listed banks. This research is quite informative for performance evaluation and improvement for general network systems.

network systems; free disposability principles; production possibility sets; data envelopment analysis; performance evaluation

2013-09-26；

2014-02-23

国家自然科学基金资助项目(71371067)

周忠宝(1977-)，男(汉族)，山东齐河人，湖南大学工商管理学院教授，博士生导师，研究方向：金融工程与风险管理、系统优化与决策.

1003-207(2015)11-0145-08

10.16381/j.cnki.issn1003-207x.2015.11.018

C931

A