基于藤Copula方法的持续期自相依结构估计及预测

叶五一，李潇颖，缪柏其

(中国科学技术大学统计与金融系，安徽合肥 230026)

基于藤Copula方法的持续期自相依结构估计及预测

叶五一，李潇颖，缪柏其

(中国科学技术大学统计与金融系，安徽合肥 230026)

本文基于Copula方法对由高频分笔数据得到的交易量持续期进行了研究。应用多元藤Copula方法对连续几个交易量持续期之间的自相依结构进行估计，在此基础上提出了一种新的条件密度函数估计方法，进而给出了交易量持续期的预测。对中国石化高频分笔数据进行实证分析的结果表明，本文模型对持续期的预测能力要明显优于EACD模型，在密度函数预测检验方面，本文模型也有更好的表现。

Canonical藤Copula； 自相依结构； ACD模型； 高频分笔数据

1 引言

持续期(Duration)是指金融市场中相邻两个事件之间的时间间隔。交易量持续期、报价持续期和价格持续期反应了市场最基本的交易信息和流动性特征，可以作为金融市场信息流动的重要指标，对持续期的研究能够揭示和解释金融市场的某些规律和现象[1]。随着获得(超)高频交易数据能力的提高，也有许多针对(超)高频交易数据的研究。然而分笔交易的时间间隔是随机的，传统的时间序列分析模型不适合描述持续期数据，需要探索新的分析方法。

Engle和Russel[2]提出自回归条件久期(Autoregressive Conditional Duration,ACD)模型可以用于描述这些点过程产生的数据。ACD的原始模型设定持续期服从线性自回归过程，而残差项分别服从标准指数(Exponent)分布或者标准化的韦布尔(Weibull)分布。为了更加准确的描述持续期数据，许多学者对ACD模型进行了扩展和改进，代表性的有一般伽玛(Generalized Gamma)分布ACD模型[3]。将Burr分布引入到ACD模型中，克服了已有ACD模型的不足，可以描述非单调的危险率函数[4]。LOG-ACD模型克服了传统ACD模型中条件期望方程的变量系数必须非负的限制，可以加入解释变量来检验市场微观结构理论[5]。

然而这些模型都是在标准ACD的框架下提出的，本质上描述的都是线性关系，除了可能导致过度参数化外，还受到严格自回归过程的影响。本文提出一种基于Copula方法的半参数模型来描述持续期数据，分析持续期之间的非线性相依结构。实际上可以将相邻的持续期数据看作是某一个多元分布的实现，我们把这个多元分布分成两部分来看，即变量的无条件边际分布和变量间的相依结构。Copula能很好地描述变量间的相依结构，利用Copula描述连续两个持续期数据间的相依结构(Temporal Dependence)，通过并对德国XETRA系统的交易数据进行了实证分析，发现基于Copula方法的模型在预测方面表现要优于ACD模型，但是没有给出具体的持续期预测结果[6]。运用Copula可以对股票市场和外汇市场的相依结构进行模拟，验证了两者收益率之间对称尾部相依的显著性[7]。本文将利用藤Copula对连续多个(大于2)持续期数据间自相依结构进行建模，得到持续期xt在给定前n个相邻持续期数据条件下的条件密度函数估计，并给出持续期预测效果和密度预测的检验。

相比较而言，二元Copula的(条件)分布函数和密度函数都比较容易得到明确的函数表达式。多元Copula的(条件)分布函数和密度函数表达式不方便表示，常见的包括多元student t Copula 和多元Gaussian Copula等，但这两类Copula在描述尾部相依性时有一定的局限，其中Gaussian Copula不适合描述尾部具有相关性的数据，Student t Copula则适合描述同时具有上尾相关和下尾相关的数据。本文引入藤Copula对多元Copula进行分解，以纳入更多的二元copula对数据进行描述。藤Copula在简单构造模块pair-Copula的基础上，提出的一种构造复杂多元相依结构新方法，它将多元联合密度函数分解成一系列pair-Copula模块和边缘密度函数的乘积，这就为二元Copula方法推广到高维情况提供了理论基础[8]。在藤Copula中应用最广泛的是C藤Copula和D藤Copula，其中C藤Copula适合描述有主导变量的数据集间的相依结构，D藤适合描述变量间地位相同的数据集。C藤Copula方法引入到金融领域中来，获得了很好的应用[9-12]。本文假定已经实现的持续期对后续实现的持续期都有影响，每棵树上都有一个主导的节点，因此我们利用C藤Copula估计多维自相依结构。藤Copula的引入，使得本文提出的半参数模型对持续期相依结构的描述更具灵活性和准确性。本文中我们将对交易量持续期进行实证分析，结果表明，本文模型在持续期的预测和密度函数检验方面都明显优于ACD模型，原因在于前者能够对多元分布进行刻画，而后者只能描述持续期均值之间的线性关系。

2 模型介绍

2.1 标准ACD模型

标准ACD模型基于GARCH模型思想建立，用于描述连续金融事件之间时间间隔[2]。令ti表示第i个金融事件对应的时间，以xi=ti-ti-1表示相邻两个金融事件之间的持续期。本文定义金融事件为完成指定的交易量(TradingVolume)，xi为完成指定交易量所需要的时间，即交易量持续期(TradingVolumeDuration)。取ψi=E(xi|Fi-1)表示xi的条件期望，Fi-1为第i-1个金融事件发生时可以得到的信息集合。标准ACD模型定义为：

xi=ψiεi

(1)

其中{εi}是独立同分布的非负随机变量序列，满足E(εi)=1。一般假定εi服从标准指数分布或者标准化的韦布尔分布，并且假定期望持续期ψi满足以下的线性形式[2]：

(2)

因为期望持续期为正，且为了保证持续期序列的平稳性，必须对参数作以下的假定：

ω,αj,βk>0 ∀j,k，

满足以上条件的就是标准ACD(r,s)模型。简单ACD模型和复杂的ACD模型在数据描述上有相近的表现[13]，本文采用εi服从标准指数分布的ACD(1,1)，即EACD(1,1)模型作为基准比较模型。

2.2 Canonical 藤(Vines)Copula 方法介绍

假定n维随机向量X=(X1,X2,…,Xn)，其联合分布函数为F(x1,x2,…,xn)，由Sklar[14]定理，多元分布函数可以通过Copula和随机变量的边缘分布Fi(i=1,2,…,n)表示如下：

F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))

多元联合密度函数则可以表示为：

f(x1,x2,…,xn)=c12…n(F1(x1),F2(x2),…，Fn(xn))·f1(x1)·…·fn(xn)

(3)

其中，c12…n(·)表示n维Copula密度函数，fi(xi)表示边缘密度函数。边缘密度函数相对来说容易估计，而多维变量间相依结构的描述却比较复杂。考虑到二元Copula选择的多样性，可以把n维Copula密度函数分解成一系列pairCopula密度函数的乘积，更方便地描述复杂的多元相依结构。对于高维Copula密度函数，pairCopula分解存在许多逻辑结构。Bedford和Cooke[8]引入了藤(Vine)图形来描述这种逻辑结构，Canonical藤是应用最广泛的逻辑结构之一，适合描述存在引导其他变量的关键变量的数据集，其结构图如图1所示。

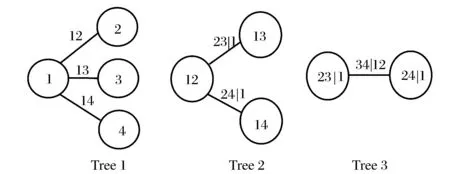
图1 Canonical 藤

根据Canonical藤的逻辑结构，我们便可以把n维Copula密度函数c(F1(x1),F2(x2),…,Fn(xn))分解成如下形式：

(4)

在上述表达式中，每个pairCopula密度函数包含一对条件分布函数F(x|υ)，它可以通过下述公式得到：

(5)

其中υj代表向量υ中第j个元素，υ-j代表从向量υ中去除第j个元素υj。

2.3 基于Canonical藤Copula方法半参数持续期模型

本文基于藤copula描述n个连续持续期之间的自相依结构，并且预测持续期xt的条件密度函数f(xt|Ωt-1)，其中Ωt-1={xt-1,xt-2……xt-n-1}为前n-1期已实现的持续期，进而在条件密度的基础上估计xt的条件均值。由于已经实现的持续期对后续实现的持续期都有影响，所以每棵树上都有关键节点，因此我们将采用Canonical藤建立模型。

根据公式(3)和公式(4)可知：

(6)

由(6)式及Bayes定理，可得在前n-1个已实现的持续期的条件下，持续期xt的条件密度为：

f(xt|Ωt-1)=ct-1,t|Ωt-2(F(xt-1|Ωt-2),F(xt|Ωt-2))·ct-2,t|Ωt-3(F(xt-2|Ωt-3),F(xt|Ωt-3))·…·ct-n+1,t|Ωt-n(F(xt-n+1|Ωt-n),F(xt|Ωt-n))·ct-n,t(F(xt-n),F(xt))·f(xt)

我们得到持续期xt的条件密度函数f(xt|Ωt-1)后，便能通过(7)式求得xt的条件期望作为对xt的预测。

ψt1=∫xtf(xt|Ωt-1)dxt

(7)

其中ψt1即为基于本文模型得到的条件期望持续期的估计。

3 基于藤Copula的持续期密度估计以及检验

3.1 持续期数据预处理

目前获得的高频数据基本都是对大盘定时扫描的结果，因此单笔交易时间间隔大多是某个数的倍数，比如3秒。这样显示单笔交易的时间ti和对应交易量vi可能并不匹配，也就是说交易量中的一部分可能在ti之前就完成了，可是由于定时扫描的原因，无法反应出精确匹配的时间ti和对应交易量vi。本文在计算交易量持续期的时候将根据交易量对单笔交易持续期进行线性拆分。

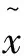
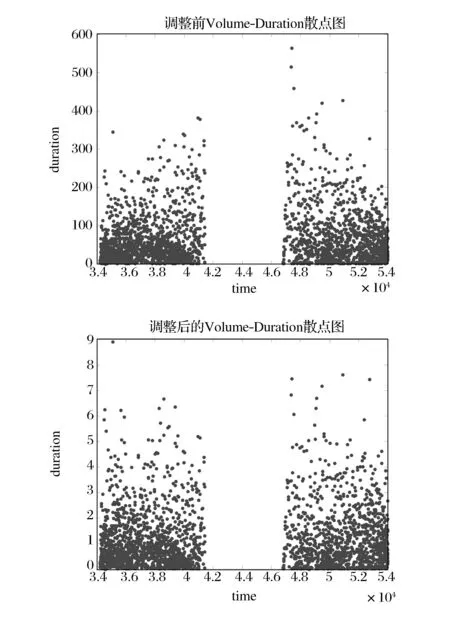
图2 调整前后的Volume Duration(单位：秒)

3.2 模型估计

关于ACD模型的估计已经有很多文献给出，不再重述[15]。下面给出本文模型的估计方法，以n=3为例，估计交易量持续期xt的条件密度函数f(xt|xt-1,xt-2) ((6)式)。

3.2.1pair-Copula参数估计

在估计Copula参数前，需要得到持续期Xt-2,Xt-1,Xt的边缘分布。根据给定的高频交易数据得到N个交易量持续期的观测值(x1,x2,……xN)，根据N个观测值构造三个向量x1,x2,x3，其中x1=(x1,x2,……xN-2)′，x2=(x2,x3,……xN-1)′，x3=(x3,x4,……xN)′。上述三个向量都有N-2个观测值，且x2,x1对应位置的交易量持续期为x3对应位置的交易量持续期的前两个已实现持续期。由于本文模型主要是为了描述连续几个交易量持续期之间的自相依结构，为了避免对边缘分布的错误设定，采用经验分布估计x1,x2,x3的边缘分布：

(8)

其中，I是示性函数，当xi,j≤r成立时取1，否则取0。

得到边缘分布后，将其代入C藤Copula的对数似然函数，便可以对参数进行极大似然估计。我们首先需要选择用何种类型的pairCopula来描述收益率序列间的相依结构，常见的二元pairCopula有Gaussian，Studentt，Gumbel和ClaytonCopula。在实证分析中，有多种途径来选择使用何种Copula来描述特定的数据集，比如，可以观察原始数据的散点图，也可以用AIC、BIC准则比较拟合结果，进而选择合适的Copula函数类型。本文中将采用极大似然方法估计C藤中每个pairCopula的参数，其对数似然函数如下：

(9)

其中n是多元Copula的维数，T表示观察值个数，θ代表pairCopula的参数集合。以上的每一个pairCopula中至少有一个参数需要被估计，这取决于选择的Copula函数类型，例如StudenttCopula有自由度和相关系数两个参数需要估计，ArchimedeanCopula通常只有一个参数需要被估计。其中条件分布函数F(xj,t|x1,t…xj-1,t)和F(xj+i,t|x1,t…xj-1,t)可以通过(5)式给出的关系通过循环计算得出。最大化(9)式，便可以得到所有参数的估计值。在对pairCopula做极大似然估计时，初值的选取非常重要，可以参见文献[9]，这里不再详述。本文模型中的对数似然函数为：

(10)

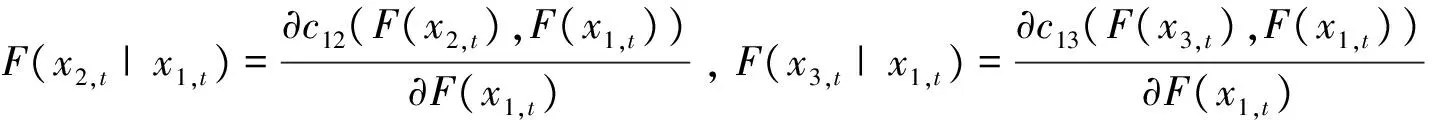
3.2.2 估计Xt的边缘密度函数

本文采用非参数核密度估计方法对Xt的密度函数f(xt)进行估计：

(11)

其中，h为选择的窗宽，K(u)为核函数。众多理论研究证明，Epanechnikov核是最优的核函数，在实证研究中本文也采用该核函数。我们也对其他核函数，例如高斯核做过分析，得到的结果几乎没有差别。Epanechnikov核函数表达式如下所示：

K(u)=0.75*(1-u2)I(|u|≤1)

3.2.3 预测条件密度函数和交易量持续期

估计出公式(6)中两个Copula密度函数ct-2,t和ct-1,t|t的参数值，每列样本持续期的经验分布函数值以及Xt的边缘密度函数值以后，便可以根据(6)式对条件密度f(xt|xt-1,xt-2)进行计算，其中xt-1,xt-2为给定的已实现的前两个持续期。xt在估计样本的最大值和最小值之间按0.01秒为间隔取值，再根据(7)进行数值积分，便可以得到预测持续期ψt1。

3.3 密度预测检验

密度预测作为针对每个样本点的概率密度分布的一种预测，在数量金融学等领域中的应用比之常见的点预测和区间预测更能满足实际需要[10]。

令p(xt|Ωt-1)为产生持续期xt的真实密度函数序列，可以通过判断预测密度f和真实密度p是否相等来评估预测的优劣[16]。由于p是不可观测的，直接判断f和p是否相等是困难的，可以基于以下命题解决[16]。

命题 1 假设p(xt|Ωt-1)是产生持续期xt的真实密度函数序列，f(xt|Ωt-1)是模型计算出的预测密度函数序列，Ωt-1持续期xt产生之前我们可以获得的所有信息。如果：

p(xt|Ωt-1)=f(xt|Ωt-1)t=1,2……N

那么根据f(xt|Ωt-1)算出的累积分布函数序列：

独立同分布与(0,1)上的均匀分布，即{zt}～iidU(0,1)。

可以基于直方图和自相关函数图来直观判断序列zt是否为独立均匀分布[16]。除此之外，本文还应用Kolmogorov-Smirnov检验(后文简称k-s检验)来评判序列zt是否为均匀分布。

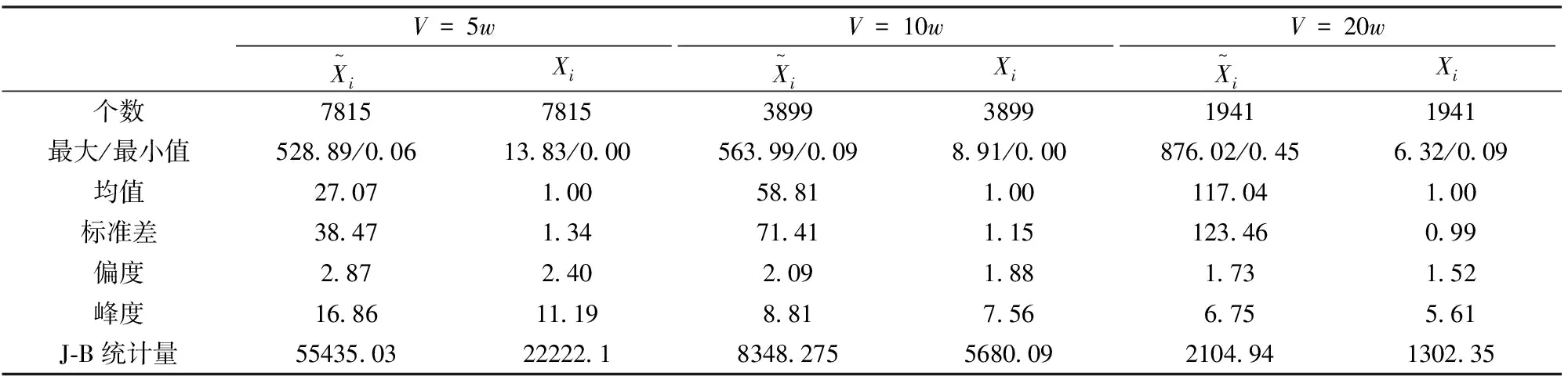
表1 数据统计特征(持续期单位为秒)

4 实证分析

4.1 数据预处理和数据描述

本文选用中国石化的分笔交易数据进行实证分析，数据从2011年8月8日到2011年9月1日。为了对模型进行参数估计和效果检验，将数据分为两段，一段从8月8日到8月22日，作为样本估计模型参数。另一段从8月23日到9月1日，用来检验模型的预测效果。考虑到集合竞价和连续竞价两种机制的相互影响，剔除了集合竞价数据。利用分笔交易数据中的单笔成交量和成交时间信息，通过对数据的线性拆分，得到完成给定交易量所需交易时间的数据，即本文中要分析的交易量持续期序列。本文分别设定交易量指标为5万股、10股和20股进行分析。数据的统计特征如表1所示。

4.2 模型估计

在该部分，以交易量取10万股为例进行实证分析的表述，5万以及20万股的实证过程完全一样，三种交易量的实证结果将同时给出。持续期的EACD(1,1)的估计结果如表2所示。

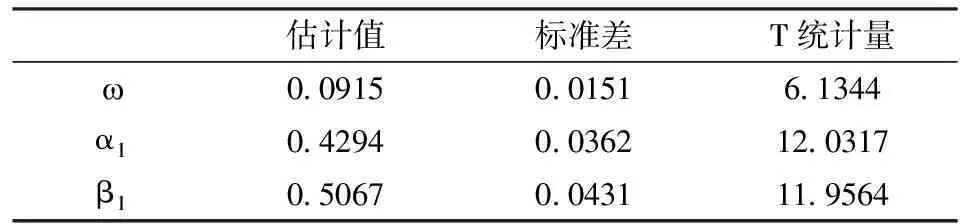
表2 EACD(1,1)估计结果

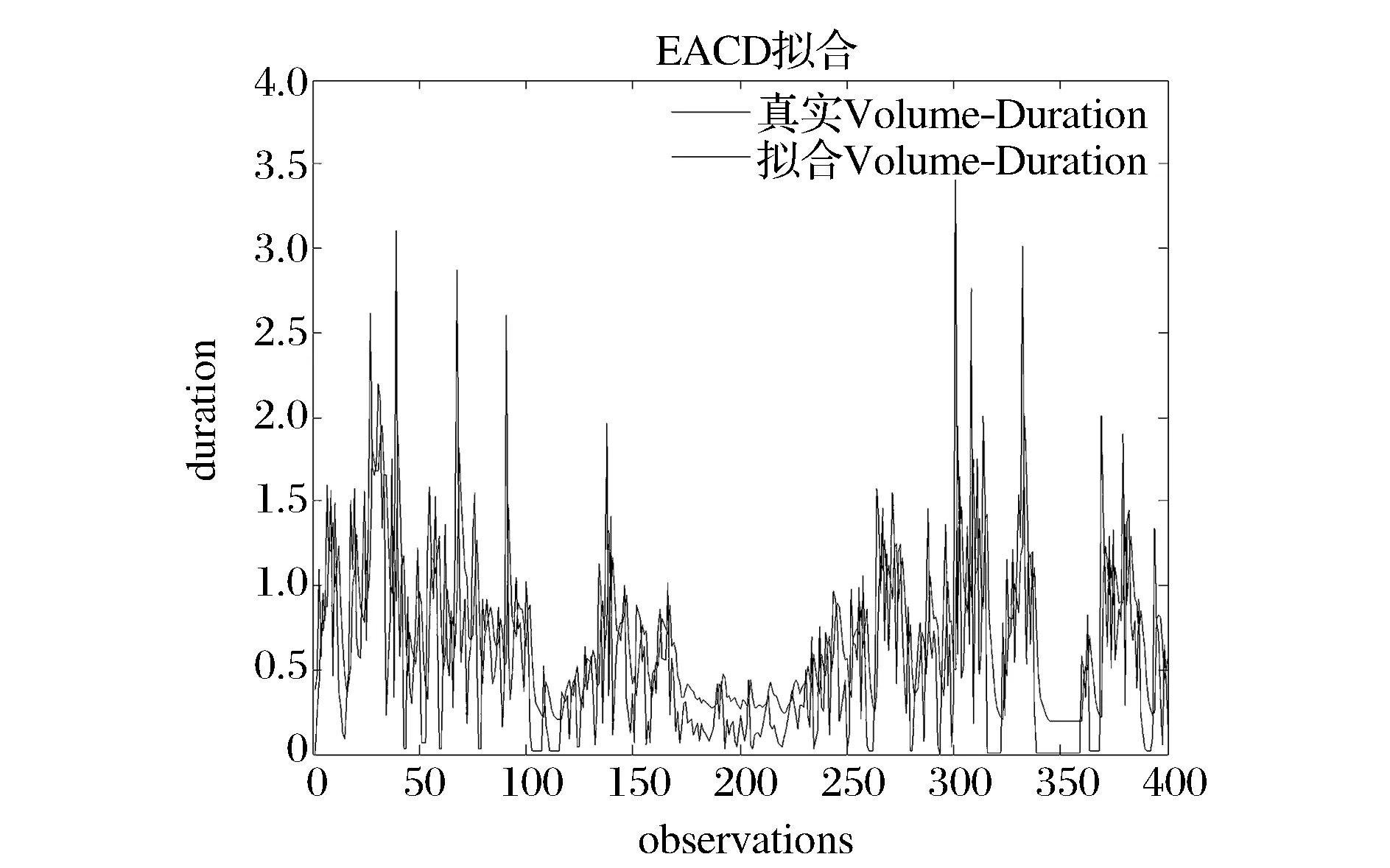
图3 EACD(1,1)拟合效果图

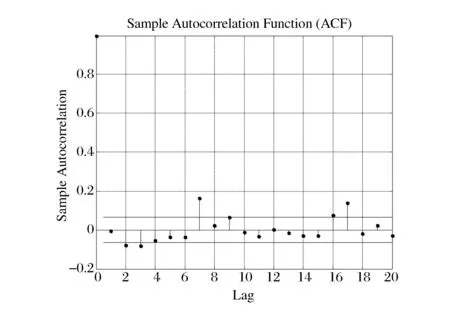
图i的自相关系数变化图

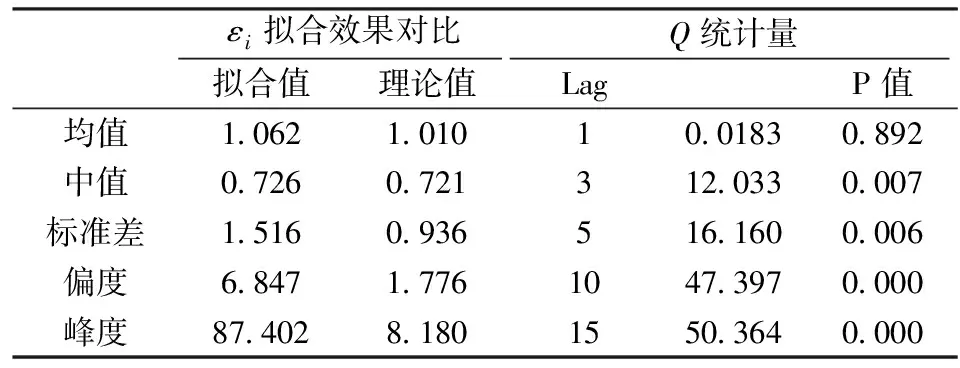
表3 εi拟合效果统计

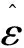
下面应用本文提出的模型进行实证分析。以n=3为例，即在得到前两个交易量持续期条件下，对下一交易量持续期进行分析和预测。由去除日内效应的交易量持续期数据，可以得到三个持续期向量x1,x2,x3，然后基于公式(8)估计出每个序列中样本值所对应的经验分布函数值。同时考虑上尾和下尾相关性，在实证分析时应用二元StudenttCopula来描述前后持续期之间的自相依结构。对于StudenttCopula，需要估计的参数有自由度ν={ν12,ν13,ν23|1}和相关系数ρ={ρ12,ρ13,ρ23|1}，其条件分布函数F(x2|x1),F(x3|x1)为：

F(xi|x1)=

(12)

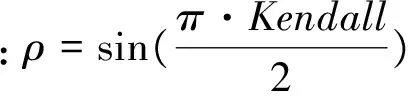
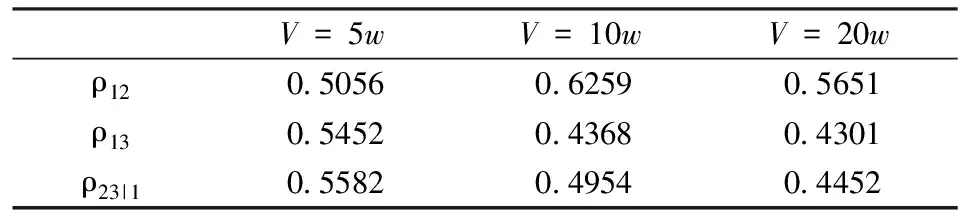
表4 相关系数估计结果

在考虑初值问题后，将数据F1,F2,F3和公式(11)带入公式(10)，令对数似然函数L最大化，即可得出Student t-Copula参数的估计值。表5给出了参数的估计结果。

从表5我们可以看出，参数估计的T统计量都大于2，说明参数估计结果显著，说明本文模型很好地描述相邻持续期之间的自相依结构关系。至此，我们完成了模型参数的估计。

4.3 模型预测效果比较

将参数带入模型，结合对Xt的核密度估计，我们便可以通过向前滚动的方法，预测出下一交易量持续期服从的条件密度函数，进而可以得到下一交易量持续期的预测。图5展示了我们通过带入去除日内效应的检验样本数据得到预测效果图。

从上图可以清晰的看出，两种模型都能对交易量持续期的聚集效应做出很好的预测。但从标出的红圈中可以看出，相比于EACD(1,1)模型，本文模型能更好的预测下一交易量持续期，特别是在交易量持续期突然变大或变小时，本文模型在大多数情况下能做出更敏感的反应。这表明，本文模型能更好的利用现有交易活跃度的信息做出准确反应。

同样我们利用本文模型对交易量取5万股和20万股时产生的检验样本持续期进行预测，并给出预测图。同样可以看出，本文提出的模型能更好地预测下一交易量持续期，特别是对较大或者较小的交易量持续期能够作出更敏感的反应。为了更明确地显示本文所提模型在持续期突然变化时的优势，我们又对图中所标出的几个关键地方给出了如下的定量结果(w=10万股时)：

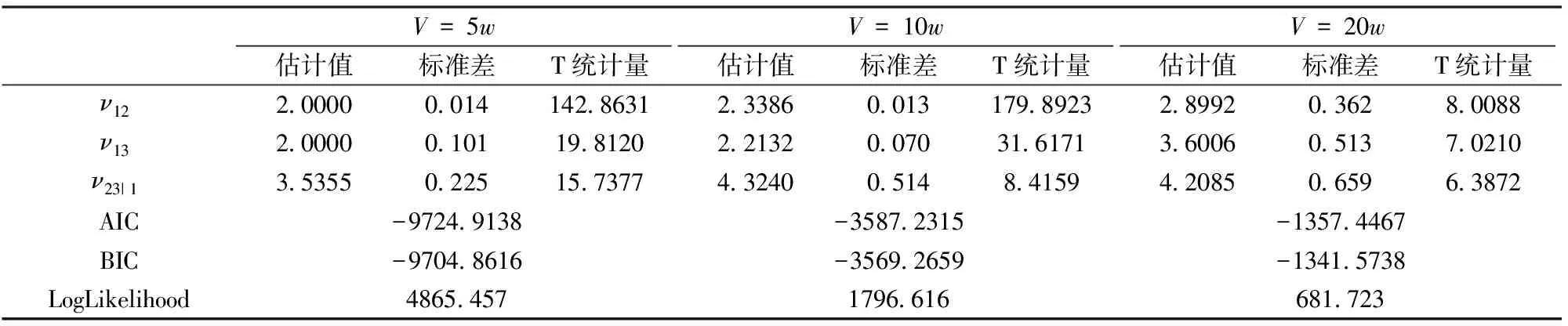
表5 pair Copula (Student t) 的参数估计结果

表6 模型预测效果定量比较(突然变化时)

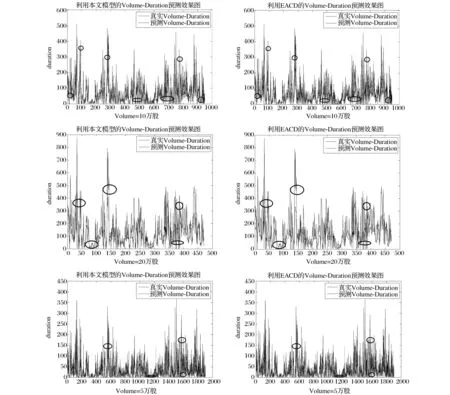
图5 交易量持续期预测效果图

由表6可以看出，对于突然变化的持续期，本文所提出的模型预测结果的相对误差要远远小于EACD模型，说明本文模型在预测突变的持续期时具有一定的优势。

通过向前滚动得到每一个交易量持续期的条件密度函数序列后，便可以通过公式(7)得到检验样本的累积分布函数值序列Zt。我们首先采用Diebold等提出的累积频率直方图来直观的观测Zt是否是均匀分布[16]。从图6我们可以看出当交易量取10万股时，直观上相比于EACD模型，本文模型产生的直方图更接近于均匀分布。当交易量为20万股时，由于数据太少，本文模型的对应的直方图也表现出剧烈的抖动。当交易量取5万股时，明显可以看出，本文模型产生的直方图表现较好。

下面基于自相关系数(ACF)分析累积分布函数值序列的独立性假设。图7给出了自相关系数随滞后阶数(Lag)变化的变化图。从图7 中可以看出，本文模型和EACD模型产生的预测累积分布函数值序列均显示出一定程度上的自相关型，拒绝了独立性原假设。

表7中给出了对原假设累积分布函数值序列服从均匀分布的K-S检验结果，当交易量取不同值时，检验结果均接受本文模型预测的累积分布函数序列服从均匀分布的原假设。

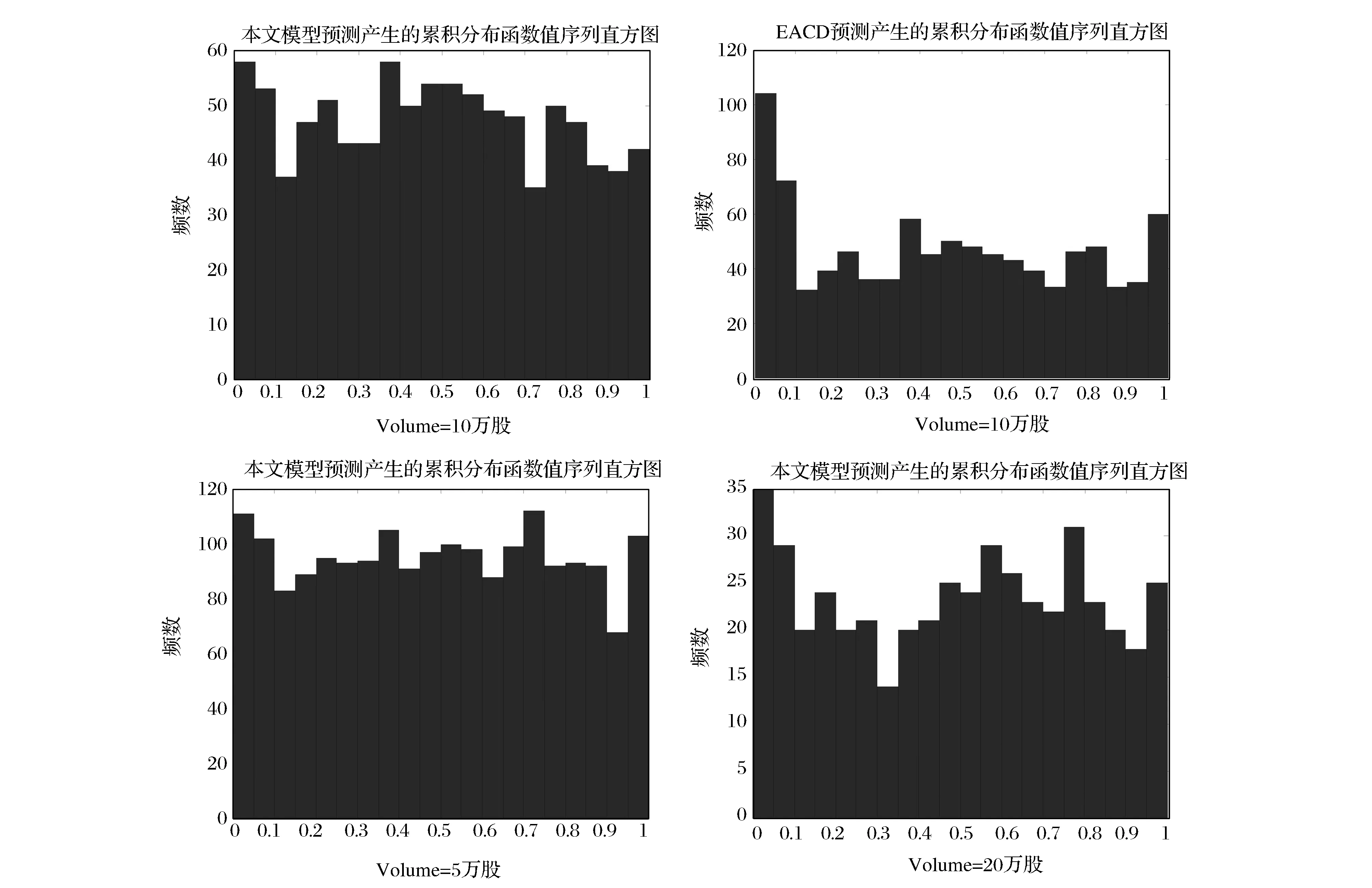
图6 累积分布函数值序列直方图

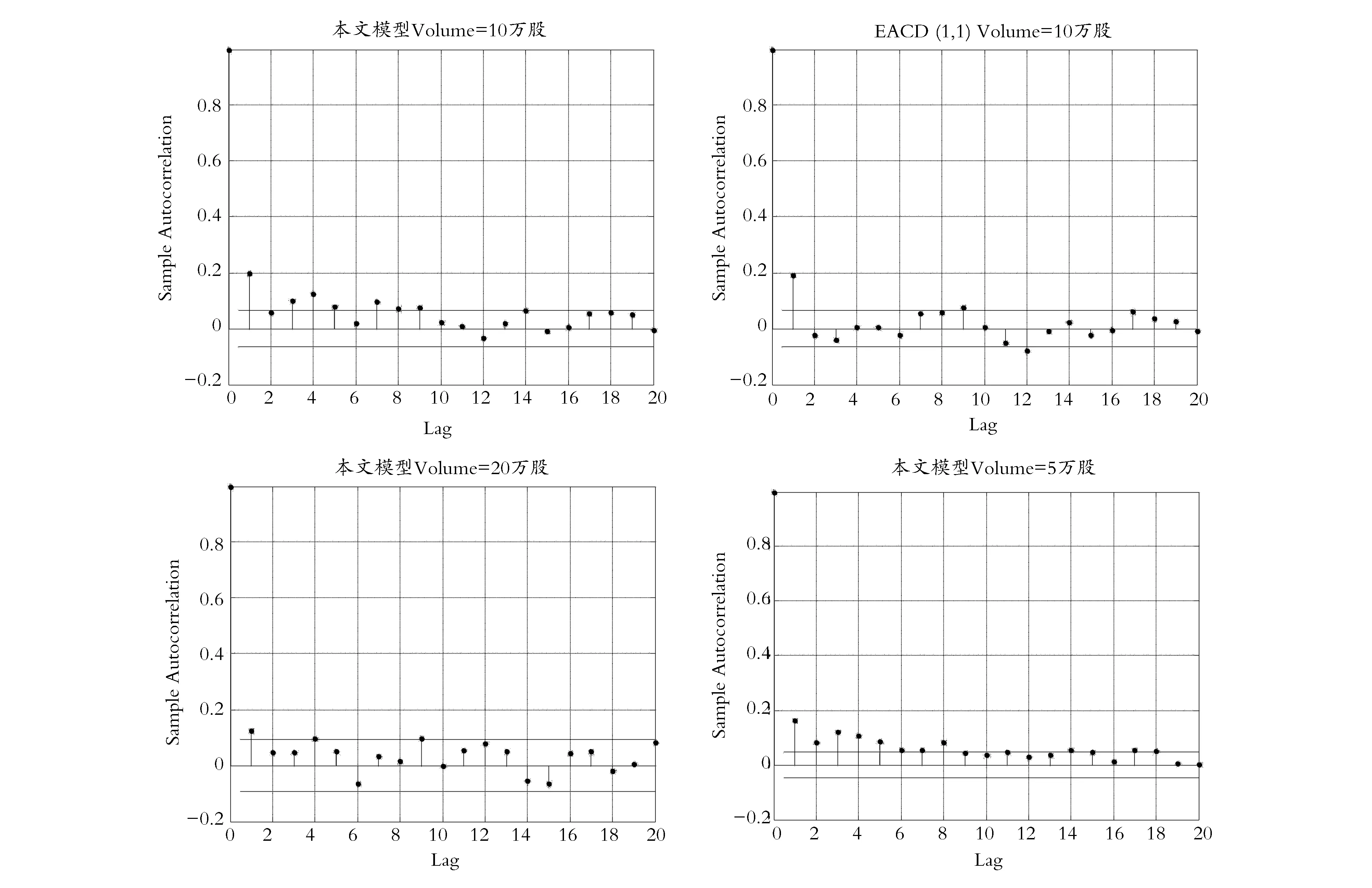
图7 累积分布函数值序列自相关系数图

V=10w(EACD)V=10wV=5wV=20wK⁃S统计量00962004120019500365p值43551e-008007730460605458是否接受1(否)0(是)0(是)0(是)

5 结语

本文提出了一个用于描述持续期序列自相依结构的基于藤Copula方法的半参数模型。为了检测本文模型的效果，我们用EACD(1,1)模型作为基准模型进行比较。ACD是参数化的且有严格自回归结构的持续期模型，这样设定会限制对持续期过程的描述。在本文中我们将相邻的n个持续期数据看作是某一个多元分布实现，我们把这个多元分布分成两部分来看，即变量的无条件边际分布和变量间的相依结构。众所周知，Copula能够很好的描述变量间的相依结构，这样基于Copula函数就可以将变量间的相依结构和变量的边际分布分离开来。在本文中，我们采用藤Copula将多元Copula分解成一系列pairCopula的乘积，以引入更多的Copula来描述相依结构。

在实证部分对中国石化的交易量持续期进行了分析，实证结果表明，EACD模型和本文模型都能很好的拟合并预测出持续期的聚集效应，但本文模型能更好的预测下一交易量持续期。尤其是在交易量持续期突然变大或变小时，本文模型在大多数情况下能做出更敏感的反应。然后我们采用Diebold等提出的密度预测检验方法对两种模型进行检验，检验结果接受了本文模型预测产生的累积分布函数序列服从均匀分布的原假设，同时拒接了EACD模型产生的累积分布函数序列服从均匀分布的原假设。但是，本文模型和EACD模型预测产生的累积分布函数序列在独立性上表现不好，表现出来一定的自相关性，这一点有待继续改进。

[1]DiamondDW,VerrecchiaRE.Constraintsonshort-sellingandassetpriceadjustmentstoprivateinformation[J].JournalofFinancialEconomics, 1987, 82(2):33-53.

[2]EngleRF,RussellJR.Autoregressiveconditionalduration:Anewapproachforirregularlyspacedtransactiondata[J].Econometrics, 1998, 66(5):1127-1162.

[3]LundeA.Ageneralizedgammaautoregressiveconditionaldurationmodel[R].WorkingPaper,DepartmentofEconomics,UniversityofAarhus, 1998.

[4]GrammigJ,MaurerKO.Non-monotonichazardfunctionsandtheautoregressiveconditionaldurationmodel[J].TheEconometricsJournal, 2000, 3(1):16-38.

[5]BauwensL,GiotP.ThelogarithmicACDmodel:Anapplicationtothebid-askquoteprocessofthreeNYSEstocks[J].AnnalesdEconomieetdeStatistique, 2000, 60:117-149.

[6]SavuC,NgWL.TheSCoDModel:Analyzingdurationswithasemi-parametriccopulaapproach[J].InternationalReviewofFinance, 2005, 5(1-2): 55-74.

[7]NingC.Dependencestructurebetweentheequitymarketandtheforeignexchangemarket-Acopulaapproach[J].JournalofInternationalMoneyandFinance, 2010, 29(5):743-759.

[8]BedfordT,CookeRM.Probabilitydensitydecompositionforconditionallydependentrandomvariablesmodeledbyvine[J].AnnalsofMathematicsandArtificialIntelligence, 2001, 32(1):245-268.

[9]AasK,CzadoC,FrigessiA,etal.Pair-copulaconstructionsofmultipledependence[J].Insurance：MathematicsandEconomics, 2009,44(2),182-198.

[10]HeinenA,ValdesegoA.AsymmetricCAPMdependenceforlargedimension:Thecanonicalvineautoregressivecopulamodel[R].WorkingPaper,SSRN,2009.

[11]JoeH,LiHaijun.Taildependencefunctionsandvinecopulas[J].JournalofMultivariateAnalysis, 2010, 101(1):252-270.

[12]RighiMB,CerettaPS.AnalyzingthedependencestructureofvarioussectorsintheBrazilianmarket:Apaircopulaconstructionapproach[J].EconomicModelling, 2013, 35:199-206.

[13]BauwensL,GiotP,GrammigJ,etal.Acomparisonoffinancialdurationmodelsviadensityforecasts[J].InternationalJournalofForecasting, 2004, 20(4): 589-609.

[14]SkalrA.Fonctionsderepartitionanddimensionsetleursmarges[J].Publicationsdel′lnstitntStatistiquedel′UniversitedeParis, 1959,(8):229-231.

[15] 李广川, 刘善存, 邱菀华. 交易量持续期的模型选择:密度预测方法[J]. 中国管理科学，2008，16(1):131-141.

[16]DieboldFX,GuntherTA,TayAS.Evaluatingdensityforecastswithapplicationstofinancialriskmanagement[J].InternationalEconomicReview, 1998, 39(4): 863-883.

[17] 叶五一，缪柏其，吴遵. 基于分位点自回归模型的动态持续期风险估计[J]，数理统计与管理，2010，29(3): 500-517.

Auto-dependenceStructureEstimatingandForecastingofDurationBasedonVineCopula

YE Wu-Yi，LI Xiao-ying，MIAO Bai-Qi

(University of Science and Technology of China, Hefei 230026,China)

In this paper, the trading volume duration sequence derived from high-frequency tick-by-tick data is analyzed by Copula method. The auto-dependence structure of several consecutive trading volume durations is estimated by multivariate vine Copula, then, a new estimating method about conditional density function forecasting is also proposed. Moreover, a new forecasting method of the volume duration is put forward. Empirical results of Sinopec show that the predictive ability of our model is much better than that of EACD, which can also be demonstrated from the density forecasting test.

canonical vine copula；auto-dependence structure；ACD model；tick-by-tick data

2014-04-12；

2015-05-03

国家自然科学基金青年面上连续资助项目(71371007)；国家自然科学基金面上资助项目(71172214)；国家自然科学基金青年科学基金资助项目(71001095)

叶五一(1979-)，男(汉族)，山东安丘人，中国科技大学统计与金融系，副教授，金融工程博士，研究方向：风险管理和金融工程.

1003-207(2015)11-0029-10

10.16381/j.cnki.issn1003-207x.2015.11.004

C931

A