灰模糊积分关联度决策模型
2015-06-01常志朋程龙生
常志朋,程龙生
(1. 安徽工业大学商学院,安徽 马鞍山 243002;2. 南京理工大学经济管理学院,江苏 南京 210094)
灰模糊积分关联度决策模型
常志朋1,程龙生2
(1. 安徽工业大学商学院,安徽 马鞍山 243002;2. 南京理工大学经济管理学院,江苏 南京 210094)
灰关联度决策模型是在假设属性之间彼此相互独立的基础上构建的,但是在很多实际问题中属性之间往往存在一定的交互作用,从而导致灰关联度决策模型失效。针对这一问题,引入模糊积分理论,构建了灰模糊积分关联度决策模型。为求解该模型,定义了基于属性权重和属性间交互度的默比乌斯变换系数,来计算2可加模糊测度,其中属性权重通过序关系分析法和施密特正交马田系统共同确定,属性间的交互关系和交互度由专家确定。以廉租房保障家庭经济状况评估为例,对灰模糊积分关联度决策模型和灰关联度决策模型进行比较验证,验证结果表明灰模糊积分关联度决策模型的决策结果更加科学合理,有较好的应用价值。
灰关联度;模糊积分;施密特正交马田系统;默比乌斯变换;序关系分析法
1 引言
灰关联度[1]是灰关联分析的基础,其基本思想是根据序列曲线几何形状的相似程度来判断序列是否联系紧密,曲线越接近,相应序列之间关联度就越大,反之就越小[2]。由于灰关联度对样本的数量和分布规律不做要求,并且计算简便,故广泛应用于多属性决策[3]、因素分析[4]等领域。自从国内学者邓聚龙教授首次提出邓氏关联度以来,大量文献从不同角度提出了很多灰关联度模型,如周期关联度[5]、相似关联度[6]、振幅关联度[7]和凸关联度[8]等。但是这些关联度模型的研究重点主要集中在灰关联系数的构建上,而如何将这些灰关联系数进行有效集成,相关研究则较少。目前主要采用加权平均的方式对灰关联系数进行集成,这种集成方式本质上是以各个属性具有线性独立关系为假设前提的,但是在实际应用中这样的假设条件很难成立。例如,对一个保障家庭的经济状况进行评估,评估属性分别为“家庭消费水平x1”、“家庭年均收入x2”、“家庭成员工作状况x3”、“家庭总资产x4”,属性的权重暂设定为0.10、0.30、0.25和0.35。通过分析可知,属性x2和x4具有一定的重复性,如果能合并成一个属性,那么合并后的属性在评估过程中会更加凸显自己的作用;属性x1和x4具有明显的互补性,这两个属性结合在一起能充分说明保障家庭的经济状况,即w1∪w4>0.45。因此在确定属性重要程度时,如果不考虑属性之间客观存在的交互性,而是简单的假设认为属性之间是相互独立,互不影响的,那么将导致评估结果失真。模糊积分[9]是定义在模糊测度基础上的非线性集成算子[10],它能够考虑属性间存在的交互性,从而为解决上述问题提供了有效工具。为此,本文结合模糊积分理论构建了灰模糊积分关联度决策模型。
2 模型构建
设A1,A2,…,Am为m个候选方案,X={x1,x2,…,xn}为方案的属性集,候选方案Ak关于属性xi的评价值为ak(xi),由此可以得到m个候选方案关于n个属性的评价矩阵为A=[ak(xi)]m×n,考虑到属性不同量纲对评价结果的影响,需要对效益型和成本型属性数据进行规范化处理,具体公式如下:
(1)
(2)
规范化后的评价矩阵为Y=[yk(xi)]m×n,现在要选出最优方案。
定义1[11]设X={x1,x2,…,xn}为属性集,P(X)是X的幂集,集函数g:P(X)→[0,1]满足下面两个条件:
1)g(φ)=0,g(X)=1;
2)K∈P(X),T∈P(X),K⊆T则g(K)≤g(T);
称g是P(X)上的一个模糊测度。
1996年Grabisch[12]从伪布尔函数[13]和黙比乌斯变换[14]出发提出了k可加模糊测度,并在此基础之上定义了2可加模糊测度。2可加模糊测度具有较强的表示能力,其计算公式如下[12]:
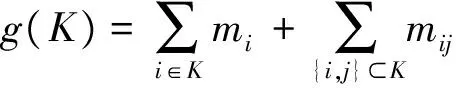
(3)
式(3)中mi是单个属性xi的默比乌斯变换系数,它是一种全局重要程度,mij是两两属性{xi,xj}的默比乌斯变换系数,它表示属性xi和xj之间的交互程度。
Choquet模糊积分[9]是定义在模糊测度基础上的一种非线性函数,Grabisch[10]提出将其作为一种集成算子来处理属性间具有交互作用的决策问题。为使灰关联度能够处理属性间的交互作用,本文利用Choquet模糊积分定义了灰模糊积分关联度。
定义2 设Yk={yk(xi)|i=1,2,…,n}为评价矩阵Y的行向量,表示候选方案Ak关于属性集X的评价向量,称之为系统的行为序列,Y0={Y0(xi)|i=1,2,…,n}为n个属性最大值组成的序列,称之为参考序列,令:
(4)
为参考序列Y0与行为序列Yk关于属性xi的灰关联系数,其中:
称:
(5)
为序列Y0与Yk的灰模糊积分关联度,其中(i)为按照γ0k(x(1))≤γ0k(x(2))≤…≤γ0k(x(n))排序后的下标,X(i)={x(i),x(i+1),…,x(n)},γ0k(x(0))=0,ρ∈(0,1)为分辨系数,一般取0.5。
定理1 灰模糊积分关联度满足灰色关联四公理:
1)规范性:0<∫γ(Y0,Yk)dg≤1,∫γ(Y0,Yk)dg=1⟸Y0=Yk;
2)整体性:∫γ(Yk,Ys)dg≠∫γ(Ys,Yk)dg,k≠s;
3)偶对称性:∫γ(Yk,Ys)dg=∫γ(Ys,Yk)dg⟺Y={Yk,Ys};
4)接近性:|y0(xi)-yk(xi)|越小,γ0k(xi)越大。
证明:
1)规范性。根据式(4)知,若Δk(xi)=Δmin可知γ0k(xi)=1;若Δk(xi)≠Δmin可知Δk(xi)>Δmin,从而(Δmin+ρΔmax)<(Δk(i)+ρΔmax),故0<γ0k(xi)≤1。再由定义2可知:
0=γ0k(x(0))<γ0k(x(1))≤γ0k(x(2))≤…≤γ0k(x(n))≤1,∅⊂X(n)⊂X(n-1)⊂…⊂X(2)⊂X(1)
进而,根据模糊测度的有界性和单调性可以得到:
0=g(φ) (6) 进一步根据式(4)知,若Y0=Yk则γ0k(x1)=γ0k(x2)=…=γ0k(xn),即: γ0k(x(0))=γ0k(x(1))=γ0k(x(2))=…=γ0k(x(n)) 当γ0k(x(0))=γ0k(x(1))=γ0k(x(2))=…=γ0k(x(n))=1时, ∫γ(Y0,Yk)dg=[1-0]g(X(1))+[1-1]g(X(2))+…+[1-1]g(X(n))=g(X(1)) 又g(X(1))=g(X)=1,故∫γ(Y0,Yk)dg=1。综上,规范性成立。 因此,∫γ(Yk,Ys)dg≠∫γ(Ys,Yk)dg,k≠s。 γks(x1)=γks(x2)=…=γks(xn)=γsk(x1)=γsk(x2)=…=γsk(xn) ∫γ(Yk,Ys)dg=∫γ(Ys,Yk)dg 4)接近性。显然成立。证毕。 3.1 定义默比乌斯变换系数 求解灰模糊积分关联度的关键是确定模糊测度,根据公式(3)可知,通过定义默比乌斯变换系数mi和mij可以计算2可加模糊测度。由于mi是一种全局重要程度,因此在定义mi时不仅要考虑属性xi的相对重要程度,还要考虑属性xi在所有属性中的重要程度;在定义mij时既要考虑属性xi和xj的相对重要程度和在所有属性中的重要程度,还要考虑属性xi和xj之间的交互度。为此,本文对默比乌斯变换系数mi和mij进行了如下定义: 定义3 设X={x1,x2,…,xn}为属性集,W={w1,w2,…,wn}为属性集X的权重集,单个属性xi和两两属性{xi,xj}的默比乌斯变换系数分别为 (7) 定理2 由式(7)计算的模糊测度为2可加模糊测度,要满足如下约束条件[12]: 1)m(φ)=0; 2)mi≥0,∀i∈X; 证明 1)m(φ)=0显然成立; 又因为-1≤ξij≤1且0≤wj≤1,故 -wj≤ξijwj≤wj,i≠j (8) 再将式(8)两边对j求和得: (9) 对式(9)两边同乘wi得: (10) 再将式(10)两边对i求和得: (11) 综上,由于P>0且wi≥0可知,mi=wi/P≥0。 故 3.2 计算2可加模糊测度 计算属性权重既要考虑决策者的主观偏好信息又要考虑决策数据的客观信息,为此我们将分别计算属性的主观权重和客观权重,然后融合为属性的综合权重。关于属性的主观权重υi(i=1,2,…,n),本文采用序关系分析法[15]计算,该方法不需要进行一致性检验计算较为简便。另外,由于属性权重是一种可加测度,是在属性之间彼此独立的基础上确定的,因此在确定客观权重ϑi(i=1,2,…,n)时,要先消除属性间存在的相关性。然而,目前常用的一些客观赋权法,如熵权法[16]、离差最大化法[17]等在确定属性权重时都不能消除属性间客观存在的相关性。针对这一问题,本文利用施密特正交马田系统(Mahalanobis-TaguchiGramSchmidt,MTGS)[18]的降维原理提出了一种能够消除属性间相关性的客观权重计算方法,具体方法如下: 为了测度属性在MTGS分类过程中的重要程度,需要用基准样本的均值和标准差去标准化待测样本,即 (12) 马氏距离是MTGS的类别判断尺度,根据矩阵Z可以计算第k个待测样品的马氏距离: (13) 由于属性之间可能存在较强的相关性,导致相关系数矩阵S不可逆,无法计算马氏距离。为解决这一问题,MTGS通过对Z中的列向量进行施密特正交来消除属性之间的相关性。 记Zi=[z1(xi),z2(xi),…,zm(xi)]T,Vi=[v1(xi),v2(xi),…,vm(xi)]T,施密特正交化的过程如下[19]: (14) 得施密特正交化矩阵V=[vk(xi)]m×n。经过施密特正交后,属性间的相关性被消除,因此矩阵V的相关系数矩阵变为 马氏距离进而变为: (15) 在MTGS中,一般用望大型或望小型信噪比来测度任意子属性集K的重要程度,这里主要讨论望小型信噪比形式: (16) 表1 属性xi和xj的交互度打分尺度 当用式(16)测度单个属性xi(i=1,2,…,n)的重要程度时,MTGS便可以达到降维的目的,这时第k个样品的马氏距离为: (17) 为确保单个属性的信噪比非负,需要对式(17)进行规范化: (18) 因此,单个属性xi(i=1,2,…,n)的重要程度为: (19) 将式(19)进行归一化得到属性的客观权重: (20) 最后,将属性xi的主观权重υi和客观权重ϑi融合为属性的权重: (21) 属性xi和xj之间的交互关系和交互度,可以根据专家经验和偏好对n个属性进行成对分析,若属性xi和xj之间具有互补性,交互度ξij>0且ξij越大互补性越强;若属性xi和xj之间具有重复性,交互度ξij<0且ξij越小重复性越强;若属性xi和xj之间彼此独立,交互度ξij=0。交互度ξij的打分标准可以参考表1。 以廉租房保障家庭退出评估为例来说明本决策模型的使用方法。我国实施廉租房制度以来,越来越多的低收入人群解决了住房问题,但是随之而来的“拒退”和“骗租”现象导致廉租房退出机制失灵,大量公共资源被占用。为全面评估保障家庭的经济状况,做到应退尽退,某市从“消费水平x1”、“家庭年均收入x2”、“家庭成员工作状况x3”、“家庭总资产x4”4个维度对5个保障家庭的经济状况进行全面评估,其中x1的数据通过社区评估获得,x2,x3和x4的数据通过保障家庭申报获得。具体评估数据如下: 步骤1 计算属性的综合权重 υ1=0.1910,υ2=0.3668,υ3=0.1365,υ4=0.3057 2)计算属性的客观权重 首选,按照属性的重要性对评价矩阵A中的列向量进行重新排序,进而构建基准样本矩阵,然后利用式(14)得施密特正交矩阵: 再利用式(18)得规范化马氏距离矩阵: 最后,利用式(20)计算单个属性的客观权重为: ϑ1=0.1993,ϑ2=0.2737,ϑ3=0.2594,ϑ4=0.2676 3)利用式(21)计算属性的综合权重 w1=0.1489,w2=0.3927,w3=0.1385,w4=0.3200 步骤2 确定两两属性间的交互度 对属性x1,x2,x3和x4之间存在交互关系进行分析,经过专家反复讨论,参考表1的交互度打分尺度,得到两两属性{xi,xj}之间的交互度,具体见表2。 表2 两两属性间的交互度 表3 默比乌斯变换系数 表4 2可加模糊测度 步骤3 利用式(7)计算属性的默比乌斯变换系数,见表3。 步骤4 利用式(3)计算2可加模糊测度,见表4。 步骤5 计算灰关联系数矩阵: 首先利用式(1)对评价矩阵A进行规范化,然后利用式(4)计算灰关联系数矩阵为 步骤6 利用式(5)计算各决策方案的灰模糊积分关联度分别为: ∫γ(Y0,Y1)dg=0.6088,∫γ(Y0,Y2)dg=0.6436,∫γ(Y0,Y3)dg=0.7266 ∫γ(Y0,Y4)dg=0.4263,∫γ(Y0,Y5)dg=0.4807 故A3≻A2≻A1≻A5≻A4,保障家庭A3经济状况最好,需要退出廉租房。 为同灰关联度进行比较,本文基于评价矩阵A采用熵权法[16]计算属性的客观权重,属性的主观权重仍然采用MTGS计算的结果,然后利用式(21)计算综合权重为: γ(Y0,Y1)=0.8121,γ(Y0,Y2)=0.5487,γ(Y0,Y3)=0.7080 γ(Y0,Y4)=0.4091,γ(Y0,Y5)=0.4475 故用灰关联度计算的排序为A1≻A3≻A2≻A5≻A4,保障家庭A1经济状况最好,需要退出廉租房。 从排序结果看,两种模型计算得到的最好经济状况保障家庭并不一致,导致这种结果出现的主要原因是灰关联度并没有考虑属性间存在的交互作用,而是简单假设属性之间是独立的,这样一方面夸大了具有重复性属性集的作用,另一方面又弱化了具有互补性属性集的作用,从而导致同本文方法的排序结果不一致。本文方法逐对分析了两两属性之间的交互关系,使各属性集的重要程度得到充分体现,从而使决策结果更加科学、合理。 灰关联度决策模型一般采用线性加权平均算子对灰关联数进行集成,因此属性之间要满足线性独立关系约束。但是在很多实际问题中,线性独立约束条件很难满足,属性之间往往具有一定的重复性或互补性,从而大大降低了灰关联度的决策效果。为破解灰关联度的线性独立约束,本文引入非线性集成算子Choquet模糊积分构建了灰模糊积分关联度决策模型,并证明了该决策模型满足灰关联四公理。关于该模型的求解,本文定义了一种基于属性权重和属性间交互度的默比乌斯变换系数,证明结果表明利用该系数计算的模糊测度是2可加模糊测度。为兼顾决策者的主观偏好信息和决策数据的客观信息,属性的权重采用主客观权重融合的方式确定。主观权重采用不需要进行一致性检验的序关系分析法计算;关于客观权重的计算,为避免属性相关性对权重的影响,本文根据施密特正交马田系统的降维原理,提出了一种能够消除属性相关性的客观权重计算方法。案例应用验证表明:灰模糊积分关联度相对于灰关联度可以更好地反映属性集在决策过程中的作用,决策结果更加科学合理。 [1] 邓聚龙. 灰色系统的基本方法[M]. 武汉:华中理工大学出版社, 1987. [2] 刘思峰,党耀国,方志耕,等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010. [3] 金佳佳,米传民,徐伟宣,等. 考虑专家判断信息的灰色关联极大熵权重模型[J]. 中国管理科学. 2012, 20(2): 135-143. [4] 卫海英,张蕾,梁彦明,等. 多维互动对服务品牌资产的影响——基于灰关联分析的研究[J]. 管理科学学报. 2011, 14(10): 43-53. [5] 施红星,刘思峰,方志耕,等. 灰色周期关联度模型及其应用研究[J]. 中国管理科学. 2008, 16(3): 131-136. [6] 马保国,成国庆. 一种相似性关联度公式[J]. 系统工程理论与实践. 2000, (7): 69-71. [7] 施红星,刘思峰,方志耕,等. 灰色振幅关联度模型[J]. 系统工程理论与实践. 2010, 30(10): 1828-1833. [8] 吴利丰,王义闹,刘思峰. 灰色凸关联及其性质[J]. 系统工程理论与实践. 2012, 32(7): 1501-1505. [9]IshiiK,SugenoM.Amodelofhumanevaluationprocessusingfuzzymeasure[J].InternationalJournalofMan-MachineStudies. 1985, (22): 19-38. [10]GrabischM.Fuzzyintegralinmulticriteriadecisionmaking[J].FuzzySetsandSystems. 1995, 69(3): 279-298. [11]SugenoM.Theoryoffuzzyintegralanditsapplications[D].Tokyo:TokyoInstituteofTechnology, 1974. [12]GrabischM.K-orderadditivediscretefuzzymeasuresandtheirrepresentation[J].FuzzySetsandSystems. 1997, 92(2): 167-189. [13]GrabischM,LabreucheC,VansnickJC.OntheextensionofPseudo-Booleanfunctionsfortheaggregationofinteractingcriteria[J].EuropeanJournalofoperationalResearch. 2003, 148(1): 28-47. [14]ChateauneufA,JaffrayJY.Somecharacterizationsoflowerprobabilitiesandothermonotonecapacitiesthroughtheuseofmobiusinversion[J].MathematicalSocialSciences. 1989, 17(3): 263-283. [15] 郭亚军. 综合评价理论、方法及应用[M]. 北京: 科学出版社, 2006. [16] 邱菀华. 管理决策熵学及其应用[M]. 北京: 中国电力出版社, 2011. [17] 徐泽水,孙在东. 一类不确定型多属性决策问题的排序方法[J]. 管理科学学报. 2002, 5(3): 35-39. [18]TaguchiG,ChowdhuryS,WuY.TheMahalanobis-Taguchisystem[M].NewYork:McGraw-Hill, 2001. [19]TaguchiG,JugulumR.TheMahalanobis-Taguchistrategy:Apatterntechnologysystem[M].Hoboken,NewJersge:JohnWiley&Sons, 2002. GreyFuzzyIntegralCorrelationDegreeDecisionModel CHANG Zhi-peng1,CHENG Long-sheng2 (1. School of Business, Anhui University of Technology, Maanshan 243002,China;2.School of Economics & Management, Nanjing University of Science &Technology, Nanjing 219004,China ) In grey correlation degree decision model (GRCM), it is assumed that all the attributes are mutually independent. However, in real decision making problems, the interaction often exists between attributes which leads GRCM to lose effectiveness. For this problem, the fuzzy integral theory is introduced and grey fuzzy integral correlation degree decision model (GRFICM) is established. To solve the model, the Mobius transformation coefficients based on weights and interaction degrees are defined to calculate 2-order additive fuzzy measures. In Mobius transformation coefficients, the weights are determined by the rank correlation analysis method and Mahalanobis-Taguchi Gram-Schmidt jointly, and the interaction relations and interaction degrees are judged by experts. An evaluation of the financial situation of low-rent housing safeguard family is provided as a practical case in order to validate GRCM and GRFICM by comparing. The validation results show that GRFICM makes the decision results more scientific and reasonable, and is more worth of spreading. grey correlation degree; fuzzy integral; Mahalanobis-Taguchi Gram-Schmidt; Mobius transformation; rank correlation analysis method 2013-05-14; 2014-08-31 国家自然科学基金资助项目(71271114,71303004);教育部人文社会科学青年基金资助项目(12YJK630005) 常志朋(1978-),男(汉族),吉林榆树人,安徽工业大学商学院副教授,博士,研究方向:多属性决策、管理综合评价等. 1003-207(2015)11-0105-07 10.16381/j.cnki.issn1003-207x.2015.11.013 C931 A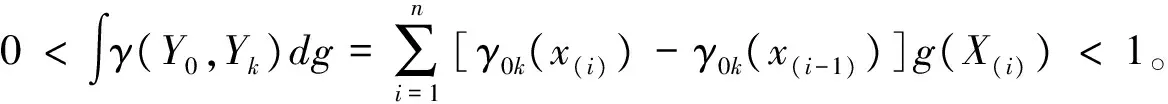
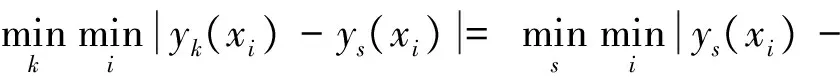
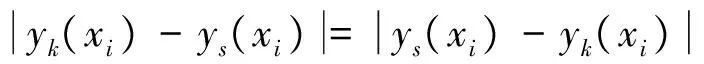
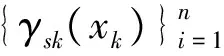
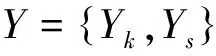
3 模型求解

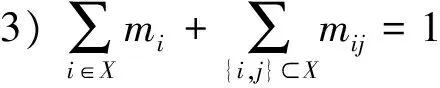
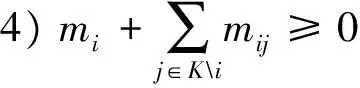
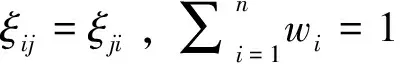
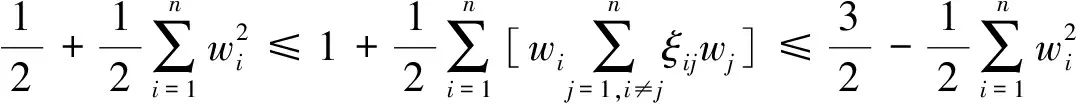
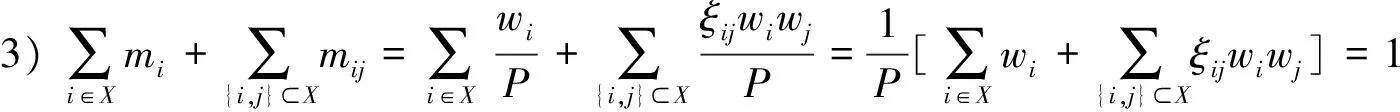
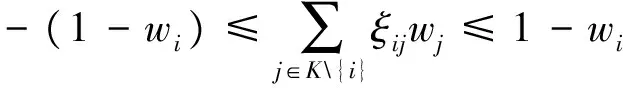

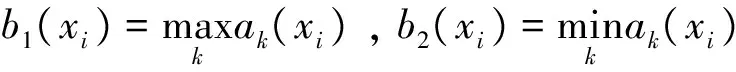
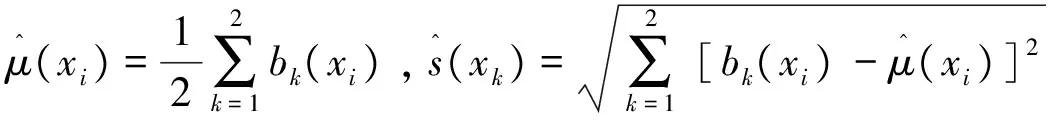

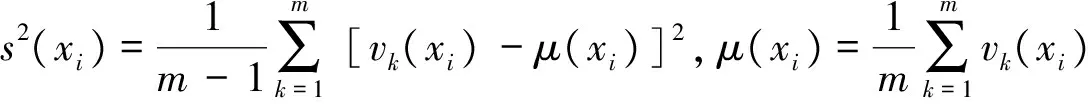
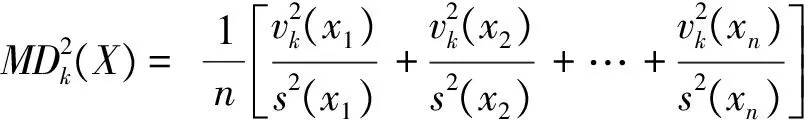
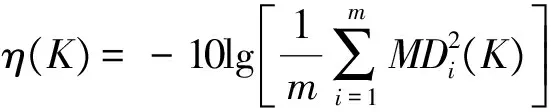


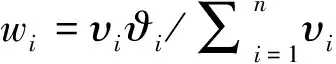
4 案例应用与分析

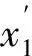






5 结语
