极端学习机算法的改进及应用研究

极端学习机算法的改进及应用研究

牛培峰∗，马云鹏，刘魏岩，卢 青，杨 潇

（燕山大学电气工程学院，河北秦皇岛066004）

摘 要：极端学习机是一种新型的单隐藏层前馈神经网络模型，其输入权值和隐藏层阈值随机设置，其输出权值解析计算得到。因此，其运算速度是传统的BP神经网络的数千倍，而且具有良好的模型辨识能力。然而，极端学习机的输入权值和隐藏层阈值是随机设定的，可能不是使网络训练目标能达到全局最小值时的最优模型参数。针对此不足，本文采用最小二乘思想确定极端学习机的输入权值和隐藏层阈值。同时，将改进的极端学习机算法应用于电站锅炉的燃烧热效率建模，并与BP、原始极端学习机、粒子群优化极端学习机和“教与学”优化极端学习机算法进行比较，证明了改进算法的有效性。

关键词：极端学习机；粒子群算法；“教与学”优化算法；最小二乘思想

0　引言

极端学习机算法（extreme learning machine，ELM）［1］是由新加坡南洋科技大学黄广斌教授于2006年提出的，是一种新型的单隐层前馈神经网络。该网络的输入权值和隐藏层阈值随机生成，输出层权值矩阵通过一步解析计算得出，避免了传统神经网络反复迭代的复杂计算过程，极大地提高了网络训练速度。极端学习机的核心思想就是将单隐层前馈神经网络的训练学习问题转化成线性最小二乘问题进行求解，通过应用Moore⁃Penrose（MP）广义逆计算输出权值［2］。目前国内外很多学者从事极端学习机的研究，提出很多有效的改进方法，如张弦等人提出限定记忆极端学习机［3］，贯序正则极端学习机［4］等各种改进型极端学习机［5⁃7］。

由于极端学习机的输入权值和隐藏层阈值是随机设定的，而在不同的输入权值和隐藏层阈值的设定情况下，网络的输出可能会不一致，所以随机值可能不是使网络的训练目标能达到全局最小值时的最优网络参数。针对此不足，文献［8］提出一种混合极端学习机算法，应用差分进化算法选择输入权值和MP广义逆解析求解输出权值；文献［9］提出一种优化前馈单隐层神经网络结构和结构参数的优化型极端学习机；文献［10］应用改进的粒子群优化算法寻找极端学习机最优的输入权值和隐层阈值；文献［11⁃12］提出一种基于改进的人工蜂群的混合型极端学习机算法，旨在选择输入权值和隐层阈值，提高极端学习机算法的泛化性能。

本文采用最小二乘法确定极端学习机的输入权值和隐藏层阈值，保证输入权值和隐藏层阈值的唯一性，该改进方法被记为最小二乘极端学习机（least square extreme learning machine，LSELM）。为了检验改进算法的有效性，分别应用LSELM、BP、ELM、粒子群优化极端学习机（particle swarm optimization extreme learning machine，PSO⁃ELM）和“教与学”优化算法［13］极端学习机（teaching⁃learning⁃basedoptimizationextremelearning machine，TLBO⁃ELM）算法建立某热电厂锅炉燃烧过程热效率模型。通过5种模型性能的比较，得出改进的极端学习机算法在保证模型正确性的基础上有较好的预测效果和良好的泛化能力。

1　基础知识

1.1极端学习机算法简介

对于任意的N个随机样本（xi，ti），xi＝［xi1，xi2，…，xin］T∈Rn，n为输入层节点个数，ti＝［ti1，i2，…，tim］T∈Rm，隐藏层节点数为m个，隐藏层激励函数为g（x），则数学模型如下所示：

式中，j＝1，2，…，N，ωi＝［ωi1，ωi2，…，ωin］T为第i个隐层节点与输入节点之间的权值，第i个隐节点阈值为bi，输出层节点与第i个隐层节点的连接权值为βi＝［βi1，βi2，…，βim］T。上述N个方程可以简写为

H被称作隐藏层输出矩阵，β是输出层权值矩阵，T是期望输出，k是输出层节点个数。

根据上述方程的最小范数二乘解的求法可得H＋是H的广义逆矩阵。

极端学习机算法步骤概括如下：

1）随机初始化输入权值和隐层阈值；

2）计算隐藏层输出矩阵H；

3）计算输出权值矩阵β＝H＋T。

1.2“教与学”优化算法简介

2010年，Rao教授受老师与学生之间的教学模式的启发，提出一种新颖的启发式优化算法，即教与学优化算法［14］。由于该算法简单易理解，修正参数少，求解精度高、速度快，收敛能力强等优点，在近几年得到广泛应用。

在TLBO算法中，学习成绩最好的个体被当做老师，老师通过自己的努力来提高班里的平均成绩；班里的学生除了跟老师学习外，学生与学生之间进行交流，取长补短，共同进步。所以，教与学优化算法分为两个阶段，即“教阶段”和“学阶段”。“教与学”算法的步骤简要概括如下：

1）初始化种群个数（学生个数），设置终止条件和适应度函数。

2）“教阶段”。

a）计算班里各门成绩的平均值，记为Mj，i，其中i表示第i次迭代，j记为第j个个体。

b）选择最优学生作为老师，计算最优值与平均值的差异系数，公式如下：

Xbest，i为i次迭代中的适应度最优值，TF为教因素。

c）学生成绩更新：

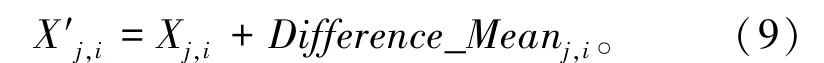
3）“学阶段”。随机选取两个不同的学生（样本），记为Xp和Xq。根据下式更新成绩：

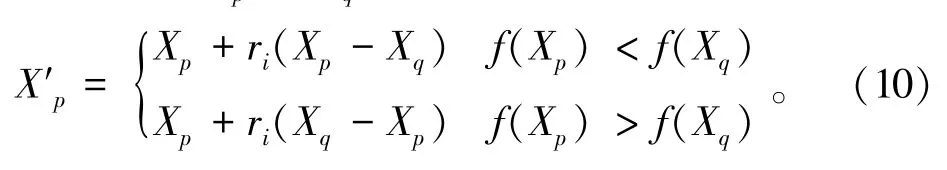
2　改进极端学习机算法

2.1基于TLBO的极端学习机

近年来，基于人工智能算法优化极端学习机模型参数成为热点。本文在ELM网络结构固定的情况下，采用“教与学”优化算法来优化输入权值和隐藏层阈值，使ELM的性能和模型参数达到最佳。

下面概括基于“教与学”算法优化极端学习机的学习过程：

1）根据样本维数和隐藏层节点数确定每一个个体的维数，应为（n＋1）×m，其中n为样本维数，m为隐藏层节点个数。

2）参数初始化。确定“教与学”优化算法中的参数，如班级大小、迭代次数、终止条件等。

3）根据目标函数公式，计算每一个个体的目标函数值，然后按升序规则对目标值排序，找出最优个体，作为教学优化算法中的“老师”。

4）“教与学”优化算法迭代寻优。通过“教阶段”和“学阶段”的学习过程，如果没有达到终止条件，返回（3）继续寻优，否则，找到全局最优个体。

5）寻优结束，保存最优个体值，即为最好的输入权值和隐层阈值。

6）将找到的最优值带入ELM中，便能求得最佳的输出权值矩阵。

需要说明的是，αi＝［ω11，ω12，…，ω1n，…，ωnm，b1，…，bm］为第i个待寻优的样本。针对优化问题要设置目标函数，这里取训练样本的均方根误差作为优化问题的目标函数，如下所示：

式中，Ntrain为训练样本的个数，m为隐藏层神经元的个数，f（·）为适应度函数。

2.2基于最小二乘算法的极端学习机

隐层输出矩阵可以作如下变形：

首先，假设隐藏层激活函数g（·）为可逆函数，则式（11）可表示为

假设存在一个矩阵P，使得

则由式（14）和（15）可知

由式（16）可以通过下式分析计算得到

根据最小二乘解的原理可以计算出

由以上推导可以得出输出权值和隐层阈值：

在输入权值和隐藏层阈值确定的过程中，虽然矩阵P是随机设定的，但与极端学习机相比，最小二乘极端学习机的随机数从（n＋1）×m降到了m×k（k为输出节点个数），所以在保证模型的训练精度的前提下，减小了随机数的影响。与此同时，最小二乘极端学习机的参数确定不是迭代更新的过程，因此比某些迭代学习的神经网络训练过程要快很多。故最小二乘极端学习机具有训练速度快，训练精度高，泛化能力强等优点。

下面简要介绍最小二乘极端学习机的学习过程：

1）确定随机生成的矩阵P；

3）通过式（19）和（20）确定输入权值和隐藏层阈值；

4）通过式（11），计算隐藏层输出矩阵；

5）根据式（6），计算输出权值矩阵。

3　仿真实验

本文以某热电厂300 MW循环流化床锅炉为对象，本文分别采集了100%、70%、50%负荷的数据，每种负荷各100组，其中包含负荷、燃料量、风量、烟气含氧量等20个对锅炉热效率有影响的参数。然后应用LSELM、BP、ELM、PSO⁃ELM和TLBO⁃ELM分别建立锅炉热效率模型。首先，将300组数据分为240组训练数据，60组测试数据。最后，设置BP、ELM和LSELM的隐藏层神经元个数为20，隐藏层激活函数为“sig”；PSO⁃ELM和TLBO⁃ELM的种群个体为40，迭代次数为200，其中c1＝c2＝1.49，适应度函数为

f（x）为模型预测值，y为目标值。本文的所有测试及实验都在运行环境为Microsoft Windows XP，CPU为Core 2 Duo T5670＠1.80 GHz，内存2 GB的计算机上完成的，仿真软件为MATLAB R2009。

本文以均方差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）作为5种热效率模型的性能指标，计算表达式如下所示：

每一种方法的测试进行30次，各性能指标参数为30次的平均值，计算结果如表1所示。当3种参数的值相对较小时，说明模型性能越好。

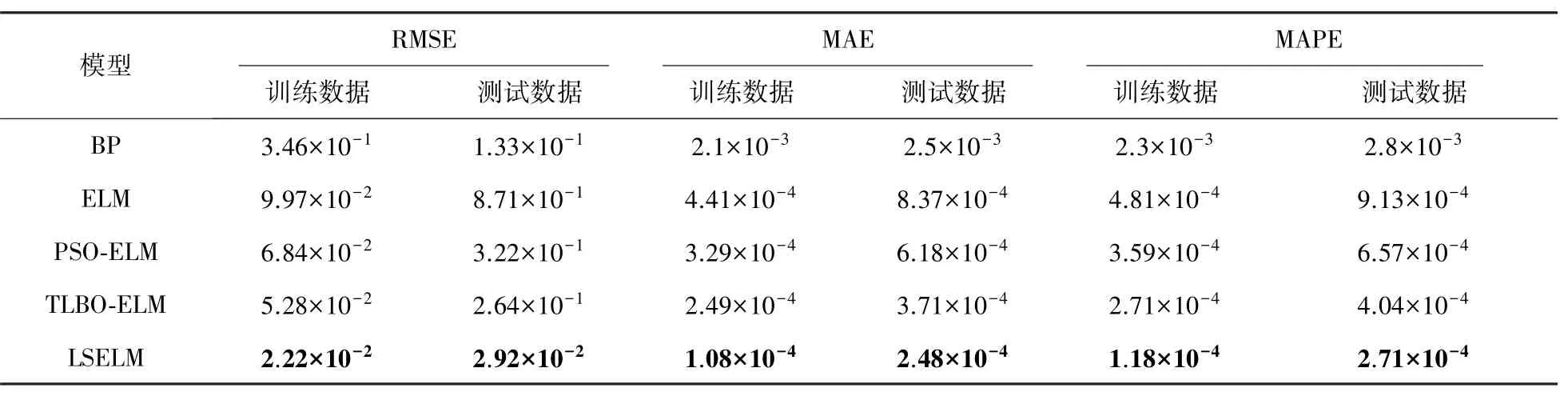
表1　各模型性能指标Tab.1　Performance index of several models

表1中给出5种方法的性能参数，表中加粗显示的数据为相对其他方法得到的最优值。表1中可以看出，LSELM的性能参数明显优于其他的几种方法，说明LSELM具有良好的辨识能力和泛化能力。而且，本文提出的LSELM优于TLBO⁃ELM，尤其是在运算时间上，LSELM平均运行时间为0.031 3 s，TLBO⁃ELM用时46.219 s，PSO⁃ELM的运行时间为541.8 s。虽然TLBO⁃ELM的运行效果不如LSELM，但是优于原始ELM和PSO⁃ELM的运行效果，其运行精度高，泛化能力强。由于本文的测试为离线模式，所以对快速性的要求不是很高，说明TLBO⁃ELM的效果是可取的，对离线建模是有意义的。综上所述，LSELM和TLBO⁃ELM具有良好的辨识能力和泛化能力。

为了更直观地比较5种方法的建模效果，给出热效率模型对比图。图1为LSELM与其他4种方法建立热效率训练模型的对比，从图中可以看出，LSELM的拟合能力优于其他方法，而且拟合曲线比较平滑，说明改进后的极端学习机算法的辨识能力有所提高。图2为5种方法的热效率预测模型对比，从图中可以看出，LSELM的拟合度仍然优于其他算法，而且平滑跟随期望值，说明改进后的极端学习机算法的泛化能力也提高了。图3～4 为LSELM与其他方法的训练和预测的相对误差对比，从图中可以看出，LSELM的相对误差波动均匀，分布集中，ELM的误差曲线波动剧烈，说明LSELM具有良好的稳定性。

图1　5种方法热效率训练模型对比Fig.1　Comparison of five methods for thermal efficiency training model

图2　5种方法热效率预测模型对比Fig.2　Comparison of five methods for thermal efficiency testing model

图3　5种方法训练相对误差对比Fig.3　Comparison of five methods for training relative error

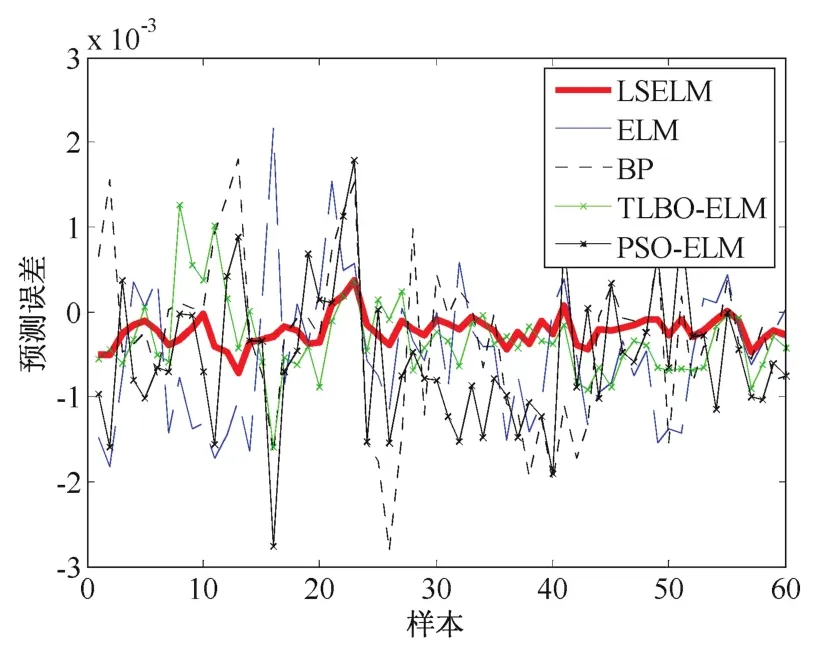
图4　5种方法预测相对误差对比Fig.4　Comparison of five methods for testing relative error

4　结论

本文针对极端学习机算法的不足，对极端学习机做出改进，提出应用最小二乘法求取极端学习机的输入权值和隐藏层阈值。将改进后的算法用于火电厂循环流化床锅炉燃烧过程热效率建模中，通过与其他4种方法的仿真实验对比，改进的极端学习机优于传统的BP神经网络、原始极端学习机和基于优化算法的极端学习机，其具有良好的辨识能力和泛化能力，有效地解决了循环流化床锅炉热效率基于机理建模困难的问题。

参考文献

［1］Huang G B Zhu Q Y Siew C K.Extreme learning machine theory and applications J .Neurocomputing 2006 70 1 489⁃501.

［2］Li G Niu P Duan X et al.Fast learning network a novel artificial neural network with a fast learning speed J .Neural Computing and Applications 2014 24 7/8 1683⁃1695.

［3］张弦 王宏力.限定记忆极端学习机及其应用 J .控制与决策2012 27 8 1206⁃1210.

［4］张弦 王宏力.基于贯序正则极端学习机的时间序列预测及其应用 J .航空学报 2011 32 7 1302⁃1308.

［5］Huang G B Wang D H Lan Y.Extreme learning machines a survey J .International Journal of Machine Learning and Cybernet⁃ics 2011 2 2 107⁃122.

［6］Li G Niu P.An enhanced extreme learning machine based on ridge regression for regression J .Neural Computing and Applications 2013 22 3/4 803⁃810.

［7］Liang N Y Huang G B Saratchandran P et al.A fast and accurate online sequential learning algorithm for feedforward networks J .IEEE Transactions on Neural Networks 2006 17 6 1411⁃1423.

［8］Zhu Q Y Qin A K Suganthan P N et al.Evolutionary extreme learning machine J .Pattern recognition 2005 38 10 1759⁃1763.

［9］Matias T Souza F Araújo R et al.Learning of a single⁃hidden layer feedforward neural network using an optimized extreme learning machine J .Neurocomputing 2014 129 428⁃436.

［10］Han F Yao H F Ling Q H.An improved evolutionary extreme learning machine based on particle swarm optimization J .Neuro⁃computing 2013 116 87⁃93.

［11］Li G Niu P Ma Y et al.Tuning extreme learning machine by an improved artificial bee colony to model and optimize the boiler effi⁃ciency J .Knowledge⁃Based Systems 2014 67 278⁃289.

［12］Li G Niu P Liu C et al.Enhanced combination modeling method for combustion efficiency in coal⁃fired boilers J .Applied Soft Computing 2012 12 10 3132⁃3140.

［13］Rao R V Savsani V J Vakharia D P.Teaching⁃learning⁃based op⁃timization a novel method for constrained mechanical design opti⁃mization problems J .Computer⁃Aided Design 2011 43 3 303⁃315.

［14］Rao R V Savsani V J Vakharia D P.Teaching⁃learning⁃based op⁃timization an optimization method for continuous non⁃linear large scale problems J .Information Sciences 2012 183 1 1⁃15.

Improvement and application of extreme learning machine algorithm

NIU Pei⁃feng，MA Yun⁃peng，LIU Wei⁃yan，LU Qing，YANG Xiao
（School of Electrical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China）

Abstract：Extreme learning machine is a novel single hidden layer feed⁃forward neural network model，whose input weights and the bias of hidden nodes are generated randomly.And its output weights are computed analytically.Consequently，the extreme learning machine owns extremely fast speed and good identification ability，which is faster than conventional BP neural network thousands imes.However，the stochastic input weights and the bias of the extreme learning machine are not the best model parameters possibly when the objective function gets the global minimum value.Therefore，the least square method is adopted to seek the appropriate pa⁃ameters of extreme learning machine.The improved extreme learning machine is applied to build the combustion thermal efficiency model of the plant boiler.Compared with other algorithms，such as BP，conventional extreme learning machine，particle swarm opti⁃mization extreme learning machine，teaching⁃learning⁃based optimization extreme learning machine，the result shows that the im⁃proved extreme learning machine is effective.

Key words：extreme learning machine；particle swarm optimization；teaching⁃learning⁃based optimization algorithm；least quare method

文章编号：1007⁃791X（2015）02⁃0127⁃06

作者简介：∗牛培峰（1958⁃），男，吉林长春人，博士，教授，博士生导师，主要研究方向为热工过程控制、智能计算等，Email：npf882000 ＠163.com。

基金项目：国家自然科学基金资助项目（61403331）

收稿日期：2014⁃06⁃19

DOI：10.3969/j.issn.1007⁃791X.2015.02.005

文献标识码：A

中图分类号：TP183