学生讲数学：实现初中数学课堂高效的催化剂

作者简介：李平（1979-），男，汉，重庆永川人，中学一级教师，教育硕士，成都经济技术开发区实验中学校，数学课程教学法。

摘要：学生讲数学，体现了“以生为本”的学生观，能大幅度提升学生的参与度，充分发挥学生的主体作用，促进学生对知识的理解、能力的生成和潜力的开发。通过圆周角定理的教学，从任务组织、课堂实施和课后反思三个方面，展示实施过程，剖析成效原因，总结教学经验。

关键词：学生讲数学；圆周角定理；课堂教学

中图分类号：G633 文献标志码：A 文章编号：2095-9214（2015）05-0049-02

学生讲数学是指课堂上围绕一个共同的数学问题，学习者用口头语言面向他人表达、解释自己的理解、想法与发现，教师与同伴通过倾听、提问、质疑、评价等方式与之对话交流的学习活动[1]。在讲数学的交流互动中，学生容易打开解决问题的思路，找到解决问题的方法；能大幅度提高学生在课堂上的参与度，充分发挥学生的主动性和主体作用，提高学生在数学课堂上的话话权，从而实现课堂的有效；是落实新课程理念中“以生为本”的学生观的体现。下面以“圆周角与圆心角的关系”为例，再现学生讲数学的过程。

“圆周角与圆心角的关系”（北师大版《义务教育教科书.数学》九年级下册第三章第3节第1课时），是理解圆周角性质和推论的基础，是解决圆的综合性问题的重要知识点，是中考的高频考点。本节课的教学目标是：经历探索圆周角定理的过程；理解圆周角概念和圆周角定理；体会分类、归纳等数学思想方法的应用。教学重点是探索圆周角定理；难点在于思维过程，理解分三种情况来证明，以及圆心在圆周角外时如何证明。我校属于农村学校，学生基础较薄弱，为了提高学生的参与度，激活数学思维，我采用了学生讲数学这一教学策略，来开启学生数学思维的大门，让学生收获知识与智慧。

一、任务组织（学生讲解准备的“四步曲”）

1、编制预习问题单。老师根据学情和课标编写预习的问题单，发给每一位学生，要求学生根据问题单预习（问题单略）。2、初检预习效果。在学生预习后，我组织学生开展了小组讨论，以提高预习的效果。3、做好任务分配。在讨论后，我向部分小组安排了明天讲数学的任务。4、学生讲解前的准备。根据预习情况，精心准备讲解内容，可向同学和老师询问、讨论或试讲，并在课前做好必要的辅助性板书。老师在学生可能会有困难的地方，给予有预见性的辅导。

二、课堂实施简录（学生讲解中：老师、“小老师”、成员的“课堂三重奏”）

我带领学生复习了圆心角的概念，通过画图复习了圆心角与弧之间的对应关系。介绍了本节课学习圆周角定理。然后组织学生按照预习的问题单来讲解。

1.认识圆周角。生1：带领同学阅读了书上圆周角的概念，指出了概念中的2个关键点：顶点在圆上和两条边要在圆内。同时画一个圆周角，讲解圆周角的初步识别。

师：肯定生1讲得直观易懂。出示下面两个问题：

⑴.如图1，判断下面图形中的∠ABC是不是圆周角，不是的请说明理由。

⑵.填空：如图2，在⊙O中，∠B是 角，∠BOD是 角，∠COD是 角。

学生独立思考后，我选取一名学生，向全班讲解展示，通过交流，让学生在实践中认识圆周角，学会判断圆周角的方法。

2.圆周角与弧的对应关系。生2：在多媒体上展示自己作出的“当圆上A、C两点确定时，过A、C两点的圆周角”，观察分析出：其顶点还没有确定，可以画出无数多个圆周角。所以弧与圆周角的关系是“一对多”的关系。

师：充分肯定生2的作图和总结。

（弧与圆周角的对应关系，学生用“一对多”来总结，确实超出了我的心里预期。）

3、圆周角与圆心的位置关系

生3：在多媒体上展示自己的作图（图3），带领同学观察分析。当圆周角是∠ADB和∠AFB时，圆心O就在圆周角的边上；当圆周角是∠AEB时，圆心O就在圆周角的内部；当圆周角是∠ACB和∠AGB时，圆心O就在圆周角的外部。所以，圆心可以在圆周角的一边上、内部和外部三种情况。我还发现，当圆周角过圆心时，顶点就是点D和点F，他们是这三种情况的分界点，当顶点在D与F之间时，如点E的位置时，圆心就在圆周角内部，当顶点在B与D之间和A与F之间时，如点C和点G的位置时，圆心角就在圆周角的外部。

师：我表扬了生3的作图和讲解。

（学生指出D和F是这三种位置关系的分界位置，这非常出乎我的意料，我的预期只要学生能找出那三种位置就很好了。我再用几何画板向学生动态展示了这三种位置关系。）

4、探索圆周角与圆心角的关系。师：引导学生通过度量，探索圆周角与圆心角之间有什么样的关系。

众生：学生们画出了如图3的图形，度量了角度，发现了圆周角等于它所对的圆心角的一半。

师：引导学生分三种情况来证明发现的结论。

生4：在图4中，利用三角形外角定理和等腰三角形两个底角相等，证明了∠AOC=2∠B。

生5：在图5中，连接BO并延长，交☉O于点D.得到2个图4那样的图形，通过两角的和证明了结论。

生6：在图6中， 连接BO并延长，交☉O于点D. 得到2个图4那样的图形，通过两角的差证明了结论。生6用书分别挡住图6中弓形BAC和扇形AOD，来观察里面包含的图4。

师：肯定了生4、生5、生6说理的正确性，特别表扬了生6用书遮挡一部分图形，突出观察主体的做法。

生7：总结出了“一条弧所对应的圆周角等于它所对应的圆心角的一半”的结论。

师：圆心角和圆周角之间可以通过弧来建立起联系。我们把这个结论称作圆周角定理。

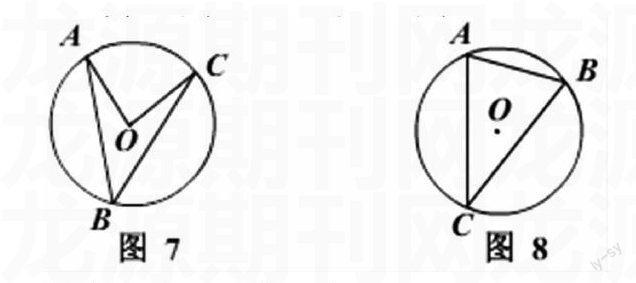
5.简单利用圆周角定理。例1：已知，如图7，在⊙O中，⑴当∠ABC=50°时，∠AOC= °；⑵当OA⊥OB时，∠ABC = °。

（直接运用圆周角定理。学生稍加思考，选取一名学生在黑板上面向全体同学讲解。）

生8：由圆周角定理，可得⑴为100°；⑵为45°.

变式1：如图8，在⊙O中，弦AB=2cm，∠ACB=30°，则⊙O的直径为 。

（学生在小组内讨论后，选取一名全班讲解。）

生9：连接AO、BO，得∠AOB=60°，△AOB就是等边三角形，得半径OA=AB=2cm，所以直径为4cm。

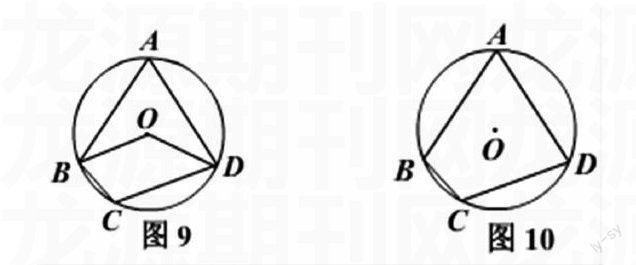
例2. 如图9，四边形ABCD的四个顶点均在⊙O上，连接 BO、DO，若∠A=80°，则∠BOD= °，∠C = °。

（本题利用圆周角定理，探索圆内接四边形性质。学生先小组内讨论，后全班讲解。）

生10：∠BOD=2∠A=160°；360°-160°=200°，∠C 就等于它的一半，为100°.

师：引导学生发现圆内接四边形对角互补的结论。

变式2：在图10中，如果∠A=70°， ∠B=100°，则∠C= °，∠D= °。

生11：利用刚得到的结论，因为∠A+∠C=180°，所以∠C=110°；同理：∠D=80°。

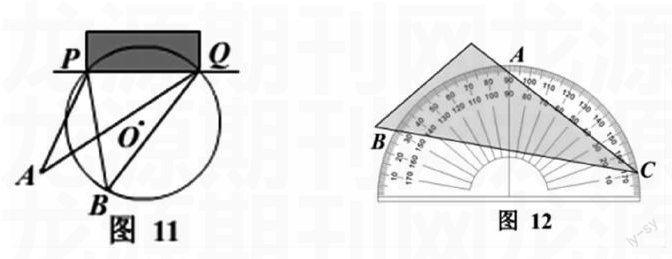
例3：如图11，PQ表示球门，现有两种射门方式：第一种是甲直接在A点射门；第二种是甲将球传给乙，由乙在B点射门.仅从射门角度考虑，应选择第 种射门方式.

（学以致用，回归教材，开发教材。师生先共同分析思路，再小组内讨论，然后全班讲解。教师巡视小组讨论，适时点拨。）

生12：利用三角形外角定理和圆周角定理，比较∠B和∠A的大小，得出结论选第二种好。

变式3：将三角形纸板按照如图12的方式放在量角器上，点C在半圆上，点A、B的读数分别为86°、30°。则∠ACB= °。

师：先师生共同分析，再小组内讨论，最后由学生讲解。

生13：得出结果为28°.

6.反思小结。师：谈谈你的收获？

生14：我知道了圆周角的概念，圆周角定理.

生15：我用分类讨论的思想，证明了圆周角定理.

师：本节课同学们讲解非常精彩，尤其是生2提出的“一对多”，非常准确；生3提出的两个分界点，分析得很深入；生7同学对第三种情况的讲解很直观；同学们对例题和变式的讲解也很准确，希望同学们在以后大胆的讲解，思维会越来越灵活，你们会越讲越优秀。

三、课后反思（学生课堂讲好数学的五要点）

学生经过认真准备，讲数学的过程进展流畅，学生的参与度较高，课堂目标的达成度较高，学生的学习潜力得到了大力的开发。

1.课堂进展流畅，得益于课前充分的准备工作。讲解问题设计的质量，直接影响到学生自学、讲解的效果。讲的难度应取决于学生的实际学习水平，以能够表达清楚为宜，遇到困难的问题，要把它分解成几个较小的问题，再分组解决。学生预习和讲解准备的落实情况，也对课堂上学生讲数学的效果有直接的影响。课前的问题清单，为学生自学和有准备的讲解指明了方向；对难点内容，通过课前辅导、问题分解，降低了难度，才获得了课堂上的流畅。

2. 学生参与度高，得益于讲数学活动的持续推进。学生不断的参与到小组讨论、同学讲解的活动中，需要不断判断他人的观点，组织自己的语言，发表自己看法，数学思维活动丰富。有效改变了传统课堂重教师讲、轻学生学、学生思维活动滞后或停留的局面，极大提升了学生的参与度，发挥学习的主动性，促进学生对知识的理解和能力的形成。

3. 课堂目标的达成度高。通过学生的讲解，学生认识了圆周角，理解并证明了圆周角定理，并尝试其应用，在思考、讨论与全班讲解中，及时复习、巩固与记忆，较好的完成了例题和变式的解答，达成了知识技能目标；分类、转化、从特殊到一般的探索过程，是过程的体验和方法的积累；倾听与表达，向他人讲解或者听取他人的讲解，促进了情感态度的发展。所以，有较高的目标达成度。

4.学生潜力得到开发。理解是数学学习的关键，“讲解性理解”是一种新的理解方式[2]。在学生讲数学的课堂上，老师为学生的讲解提供了很多的机会，能极大的促进学生对知识的理解，能丰富课堂形式的多样性，消除过去老师单一讲解方式带来的学习疲倦。同时，对学生的表达能力，与人交往的能力等都是很好的锻炼，是对学生潜力的大力开发。

5. 信任学生是打开学生讲数学大门的钥匙。有时我们不愿放手，怕学生讲不清楚，耽搁时间又要重新去讲，究其原因，是我们对学生的信任不够。事实上，只要我们给学生机会，他们常常能带给我们意想不到的惊喜，比如学生把弧与圆周角的关系总结为“一对多”，把圆周角过圆心的位置总结为三种不同位置的分界点，这都是他们带给我的惊喜。

学生讲解数学，作为探索中的一种教学方式，还有很多理论与实践问题需要深入研究，我将在以后的工作中加强理论与实践的结合，不断的补充和完善。

（作者单位：成都经济技术开发区实验中学校）

参考文献：

[1]王富英，王新民. “学生讲数学：一种重要的数学学习方式”[A].首届华人数学教育会议论文集[C]， 2014，112-115

[2]王新民，王富英.“讲解性理解”的基本含义与教学价值[J]. 内江师范学院学报，2010，25（4）：89-94.