一道课后习题的多种解法与思考

王永利

【摘要】 一道普通的课后习题，只要我们深入研究，往往会发现多种解法. “已知⊙O外一点P，你能用尺规过点P作⊙O的切线吗？你有几种方法？”对于这道课后习题，我们可以利用直径所对的圆周角是直角作图;也可以利用等腰三角形的“三线合一”作图;可以通过构造全等的直角三角形作图：（1）利用圆中的条件构造全等的直角三角形;（2）借助圆外任意直角构造全等的直角三角形. 以上解法，丰富多彩，细细品味，每一种解法都有它的独到之处.

【关键词】 切线;不同解法;圆周角;三线合一;直角三角形

北师大版九年级下习题3.8问题解决：“已知⊙O外一点P，你能用尺规过点P作⊙O的切线吗？你有几种方法？”此题考查学生灵活运用所学知识解决问题的能力，有一定的难度. 解决该题的关键是如何作以半径为一边，顶点在圆上的直角. 方法1：利用直径所对的圆周角是直角作图（如图1）

作法：①连接OP，以OP为直径作⊙C，与⊙O交于A，B两点;

②作直线PA，PB.

则直线PA，PB即为⊙O的切线.

证明：连接OA，OB.

由OP为⊙C的直径，所以∠OAP = ∠OBP = 90度.

又OA，OB为⊙O的半径，所以直线PA，PB即为⊙O的切线.

方法2：利用等腰三角形的“三线合一”作图（如图2）

作法：①连接OP，交⊙O于点D，延长DO交⊙O于点C;

② 分别以点O、点P为圆心，以直径CD长、OP长为半径画弧，两弧交于点Q;

③ 连接OQ，PQ，OQ交⊙O于点A，作直线PA.

则直线PA为⊙O的切线.

证明：∵OQ = CD = 2OA，∴ OA =  AQ.

∵ PQ = PO，∴ ∠OAP  = 90度.

所以直线PA为⊙O的切线.

方法3：构造全等的直角三角形作图

（1）利用圆中的条件构造全等的直角三角形（如图3）

作法： ① 连接OP，交⊙O于点C;

② 过点C作OP的垂线MN;

③ 以点O为圆心，OP长为半径画弧，交直线MN于点D，E;

④ 连接OD，OE，交⊙O于点A，B，作直线PA，PB.

则直线PA，PB为⊙O的切线.

证明：∵OP = OD，OA = OC，∠AOP = ∠COD，

∴ △AOP ≌ △COD. ∴ ∠OAP = ∠OCD = 90度.

同理可得∠OBP = ∠OCE = 90度.

则直线PA，PB为⊙O的切线.

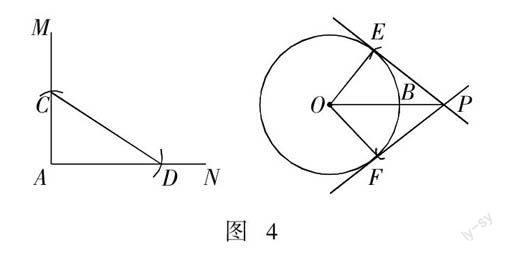
（2）借助圆外任意直角构造全等的直角三角形（如图4）

作法：①连接OP，交⊙O于点B;

② 任意作∠MAN = 90度，在边AM上截取AC = OB;

③ 以点C为圆心，OP为半径画弧，交AN于点D，连接CD;

④ 以点P为圆心，AD长为半径画弧，交⊙O于点E、点F，连接OE，OF，作直线PE，PF.

证明：∵AC = OE = OF，AD = PE = PF，DC = OP，

∴ △ADC ≌ △EOP ≌ △FOP

∴ ∠OEP = ∠OFP = ∠CAD = 90度

则直线PA，PB为⊙O的切线.

回顾与思考： 以上解法，丰富多彩，细细品味，每一种解法都有它的独到之处.

解法1紧扣本章所学内容，即在圆中直径所对的圆周角是直角. 通过连接OP，并以OP为直径作圆，从而得到直角. 方法简洁明晰.

解法2利用等腰三角形的“三线合一”作图. 首先利用圆规画出等腰三角形，而底边的中点恰好也在圆上，从而就有底边上的中线，由等腰三角形的“三线合一”即可得到直角. 该方法体现了思维的灵活性.

解法3灵活运用全等三角形的构造方法. 变式1是在圆的基础上构造全等的直角三角形. 变式2是构造全等三角形方法的一般化，是拓广. 该方法体现了思维的广泛性和深刻性.  解法中的多条辅助线充满了智慧，把陌生的作图问题转化为熟悉的全等图形问题，从而使问题迎刃而解.

一道普通的课后习题，只要我们深入研究，往往会有多种解法，这些解法中往往会包含着多种数学思想与方法，每一种解法的诞生都不是凭空而降的，它来源于平时积累的知识与方法、灵感与智慧、思维与创造.因此，在日常教学中，我们要重视在知识和技能中所蕴含的数学思想方法的教学，从初一做起，循序渐进地让孩子们掌握数学的知识和技能，尤其是数学思想方法，逐步形成能力，运用自如.在日常学习中，我们要重视对解题方法的总结，通过一题多解、一题多变，举一反三、触类旁通，从思维的发散到集中，总结规律性的东西，形成学习经验，提高解题效益，让学生的思维能力得到发展.