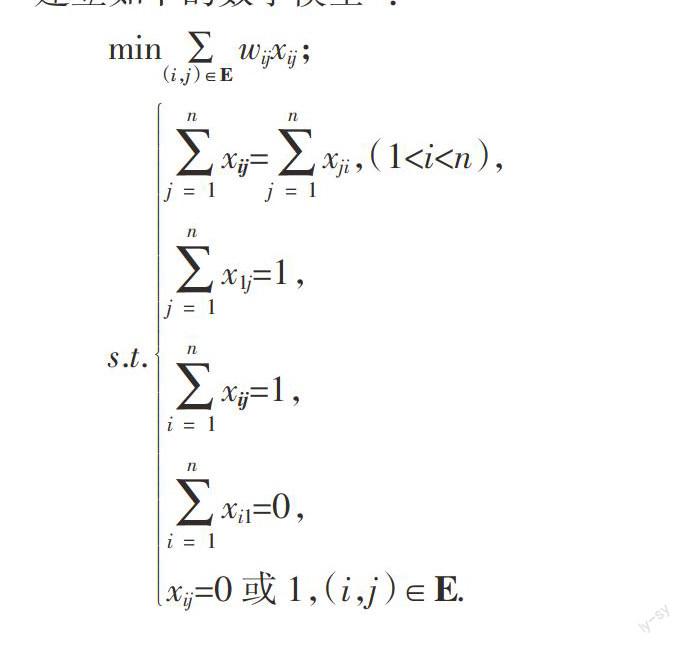在图论课程中融入数学建模思想的教学改革初探
2015-05-30孙培刘凯曾俊杰杨本朝
孙培 刘凯 曾俊杰 杨本朝
[摘 要]基于图论教学的重要性及图论课程的教学现状,可以将教学建模的思想和方法融入图论教学中,以开拓学生的视野,培养学生学习数学的兴趣和应用意识,提高学生应用数学知识和方法解决实际问题的能力。
[关键词]图论 数学建模 优化问题 教学改革
[中图分类号] G642 [文献标识码] A [文章编号] 2095-3437(2015)08-0118-02
一、引言
图论是离散数学和组合数学的重要分支,它以图为研究对象,这种图由若干给定的点及连接两点的边所构成,通常用来描述某些事物之间的某种特定关系。图论起源于18世纪著名的哥尼斯堡七桥问题,现已发展成为一门应用数学课程。由于自然科学中许多领域的问题可以转化为图论问题,故图论越来越得到相关领域和专家的广泛关注。下面笔者谈谈图论课程的教学现状以及在图论课程中融入数学建模思想的教学实践。
二、图论课程的教学现状
图论和其他数学课程一样,有着大量抽象的、深奥的概念与理论。如果教师按常规的教学方法,将授课重点放在图论基本理论的传授上,放在定理的证明中,学生往往会感到枯燥乏味,缺乏学习兴趣。另外,学生学习图论这门课的目的是通过对图论中各种算法的学习,培养自己的编程能力和解决实际问题的能力。这就对我们的图论教学提出了新的要求。数学建模是联系数学理论与实际的一座桥梁,是解决实际问题的强有力的工具。因此,我们在图论教学中可融入数学建模思想,突出知识的应用,让学生带着问题来,在解决问题的过程中与教师交流,课后带着问题去,把数学建模的意识、思想贯穿在图论的每一个问题的解决过程中,最后归纳总结出数学思想和方法,让学生学会如何运用数学理论去解决实际问题[1],从“学数学”到“用数学”,培养学生分析问题、解决问题的能力。
三、在图论课程中融入数学建模思想的教学实践
1.充分利用网络资源,进行资源型学习。随着计算机网络技术的飞速发展,互联网所承载的信息量越来越大,更新速度越来越快,这就使得学习的资源由传统的课本向丰富的网络资源扩充。学生可利用网络查询知识,共同讨论。教师的教学手段也发生了改变,从传统的传道授业变成了注重教给学生如何利用网络获取知识,查找文献。笔者在教学中充分利用网络资源,不仅提高了教学效率,而且培养了学生的自学能力和创新能力。
例如,在备课时,充分利用互联网,获取大量的图论信息资源,特别是国家精品课程等网站,提供了教学大纲、教学录像、电子教案等教学素材,教师可参考、借鉴同行的教学思路和课件,博采众长,提高备课的效率和质量[2]。同时,图论中的许多问题有多种算法,教师授课时不可能面面俱到,而应重点讲解比较经典和基础的算法,对于其他算法,可以给出名字,鼓励学生课后自己查找文献资料。这样,既讲清楚了如何解决问题,又培养了学生的自学能力。
2.以解决实际问题为目的,注重建立问题的数学模型。图论起源于实际问题,与实际生活联系非常紧密,图论中的许多问题都可以建立数学模型,从而优化问题。授课中,我们不仅要讲授解决问题的经典算法,而且要建立问题的数学模型,将数学建模思想融入其中,鼓励学生用多种方法解决问题。
例如,对于最短路问题,有经典的Dijkstra算法,同时我们经过分析,可以引入0-1决策变量xij,即当边(i,j)在最后选定的最短路径上时,xij=1,否则为0,因此可以建立如下的数学模型[3]:
min■wijxij;
s.t.■xij=■xji,(1对于这两种方法,要讲清楚优缺点:Dijkstra算法对权为负的问题不适用,但是可以求一固定点到其他点的最短路径;而建立数学模型的方法不受权为负的限制,但稍显死板,如果变换一个顶点,就要重新编程求解。
再如,对于最小生成树问题,有Kruskal算法和Prim算法,两种算法的复杂度分别为O(mlogm)和O(n2)[4],其中m为边数,n为点的个数。因此,他们的适用范围是不同的,前者适用于边比较少的图,后者适用于点比较少的图。经过这样以应用为目的的教学,使学生更加深刻地理解了问题,并为其以后的学习和工作中打下基础。
3.在教学过程中强调数学思想。在教学过程中,要培养大学生的创造性思维,就要以数学思想为灵魂,统帅整个教学过程,图论的教学更不例外。我们既然强调用数学建模思想解决图论问题,就要将这个理念贯穿教学的全过程,同时注意归纳总结。
例如,在对许多问题进行建模的过程中,我们都是建立了一个决策变量xij,然后用这个决策变量来分析问题,得出数学模型。因此,这种引入决策变量,巧妙地将图论中的问题用矩阵表示出来的思想和方法值得我们学习。这样的教学让学生感受和了解数学知识的发生和形成过程,引导学生如何将实际问题转化成数学问题,然后用数学思想和方法来解决。
4.结合课程特点,精选教学内容,对传统内容优化组合,推陈出新。对于传统的图论教材,可删除陈旧的内容和复杂的推理过程,将授课重点放在图论思想的讲述和算法实现上。
例如,大部分教材将最小生成树问题单独作为一章来讲解,将欧拉问题和旅行商问题作为一章来讲解。但由于我们在教学过程中注重启发学生建立数学模型,并用Lingo数学软件编程进行解决,因此我们对内容进行了重新优化组合。由于最小生成树问题和旅行商问题的数学模型、数学思想大致相同,因此我们将这两部分作为一章来讲解,使学生在建立数学模型的过程中深刻理解这两个问题。
再如,许多教材把匹配问题与指派问题放在了网络流问题的前面,但我们通过查阅文献发现,二部图的最大匹配问题可以转化成网络的最大流问题,从而可以用网络流的算法求解,因此我们将内容重新调整,把网络流问题放到匹配问题前面讲解。同时,在讲解欧拉问题时,对不是欧拉图的图G求欧拉回路,首先要把它变成欧拉图,再用Fleury算法求解。在将图G转化成欧拉图的过程中,需要求度数为奇的顶点的最小权匹配,因此,在授课时,我们也把匹配问题放到欧拉图前面讲解。
经过这样的组合教学,学生感觉到所学知识是一个整体,而不是问题与问题是相互独立的关系。同时,看似两个不相关的问题,经过分析,能够转化成一样的问题,也锻炼了学生思考问题、分析问题和解决问题的能力。
5.增加Lingo数学软件的介绍与应用,培养学生的实践创新能力。传统的基础教学注重理论性,缺乏实际应用,对后续的其他专业课程帮助不大。我们要在授课中突出知识的应用思想,讲解相应的数学软件,培养学生的动手能力。图论中的许多问题都能转化成优化问题,而求解优化问题非常好用且容易上手的软件就是Lingo软件。因此,我们在授课时将Lingo软件作为辅助教学的工具,将理论教学和实验演示融为一体,使学生更加深刻地理解相关理论和算法,提高课堂教学效率。实践证明,在图论教学中使用数学软件,有助于加深学生对抽象理论与算法的理解,调动学生自主学习和创新学习的积极性,提高学生的动手能力和科研能力。
四、结束语
总之,在图论教学中融入数学建模的思想和方法,顺应了数学教学改革的方向,调动了学生的学习主动性和积极性。教师通过布置大作业、上讨论课,使学生对所学知识进行加工转换、重组再现,锻炼了学生的数学思维,提高了学生的编程能力和实践创新能力,取得了良好的教学效果。
[ 参 考 文 献 ]
[1] 裴振奎,徐九韵.MATLAB在“图论”课程教学中的应用[J].计算机科学,2010,37(7):108-110.
[2] 康云艳,杨暹,郝振萍.网络资源在《蔬菜栽培学》教学中的应用[J].安徽农业科学,2011,39(9):5628-5629.
[3] 谢金星,薛毅.优化建模与lindo / lingo软件[M].北京:清华大学出版社,2005.
[4] 龚劬.图论与网络最优化算法[M].重庆:重庆大学出版社,2009.
[责任编辑:钟伟芳]