新型四线圈无线能量传输系统的效率建模

吴朝晖 万 如 李 斌

（华南理工大学电子与信息学院，广州 510640）

作为一项具有划时代意义的高新技术，电磁谐振式无线能量传输（wireless power transfer，WPT）技术传输效率高，距离远，更加安全、可靠、灵活，满足了便捷性和安全性生产及使用的需要，成为当前该领域的研究热点[1]。

对于电磁谐振式WPT 系统，谐振回路的建模是国内外学者研究的主要内容之一，系统最初是由两个谐振回路构成，文献[2-3]研究了两线圈系统及其频率分裂现象，然而在两线圈系统中，随着传输距离的增大，两个谐振线圈间的耦合强度会迅速减弱。文献[4-5]在构建了传统的四线圈模型，然而在此模型中，电源线圈和负载线圈不参与谐振，谐振线圈间的耦合强度没有达到最高。为了进一步优化WPT系统的传输性能，文献[6]提出了一种新型的四线圈结构，此结构中四个线圈均参与谐振，尺寸相当，第一个和第四个谐振回路的Q值也设计得很高，并且交叉耦合达到最大，此结构能够同时提高效率和传输功率。

可以看出，两线圈系统和传统四线圈系统的系统性能研究较为成熟，但是鲜有学者对新型四线圈系统的频率特性和耦合特性进行研究。新型四线圈系统中效率的频率分裂现象更为复杂，且每相邻两个谐振线圈之间的耦合系数均是影响系统性能的重要因素，那么找到最佳相邻耦合系数，以及设计出四个谐振线圈之间的最佳距离成为新型四线圈系统的重要研究内容。本文根据电磁谐振方式传输能量的基本原理，构建包含四个谐振回路的系统架构，用电路理论的分析方法对系统效率模型进行推导与分析，研究其频率分裂现象，通过分析效率特性找到四个谐振线圈之间的最佳耦合系数，进而完成四个线圈最佳距离的设计。

1 新型四线圈WPT 系统效率建模

四线圈结构的电磁谐振式无线能量传输系统的简化模型如图1所示，V1是交流电源，其输入电压为V1，r是电源内阻，Li、Ci、Ri分别是第i（i=1、2、3、4）个谐振回路中的电感、电容和寄生电阻；RL是负载电阻。Mij、kij分别是第i个和第j个线圈之间的互感和耦合系数，其中（i=1、2、3、4，j=1、2、3、4）。与相邻耦合系数相比，交叉耦合系数较小，可忽略不计。

图1 新型四线圈WPT 系统模型

四个谐振回路的参数完全对称：L1=L2=L3=L4= L，C1=C2=C3=C4=C，R1=R2=R3=R4=R。工作角频率为ω时，四个谐振回路的电抗相同，为X=ωL-1/ωC。四个谐振回路的阻抗分别为Z1=r+R+jX，Z2=Z3=R+jX，Z4=RL+R+jX。相邻两个谐振线圈之间的互感分别为M12=k12L，M23=k23L，M34=k34L。

由基尔霍夫电压定律得出四个回路的电压方程为：

由式（1）可得电源谐振回路和负载谐振回路的电流，分别为I1、I4，均为顺时针方向。将I1和I4归一化处理，表示如下

其中，

由式（2）可得输入功率和负载功率分别为

根据输入功率和传输到负载的功率的表达式（2）、（3）和（4），可以得到系统的效率为

2 效率的频率分裂现象分析

利用上面建立的效率模型对新型四线圈WPT系统效率的频率特性进行分析。系统的自谐振频率为了便于观察，将工作频率f与自谐振频率f0归一化处理。图2是在f /f0和耦合系数同时变化时，系统效率的变化趋势。电感为80μH，电容为2.2 nF，当k23=0.5，k34=0.2 固定不变时，效率随f /f0和k12的变化趋势曲线如图2（a）所示；当k12=0.6，k34=0.2 固定不变时，效率随f /f0和k23的变化趋势曲线如图2（b）所示；当k12=0.6，k23=0.5固定不变时，效率随f /f0和k34的变化趋势曲线如图2（c）所示。与两线圈系统负载功率的频率分裂现象不同的是，四线圈系统效率的频率分裂现象更为复杂，会出现三个不同的分裂频率，其频率分裂特性如下所述。

图2 效率对f/f0、k12、k23 和k34 的变化趋势

1）随着频率由低到高增大，效率会出现三个极大值，效率三个极大值对应的频率即为三个分裂频率，依次为f01，f0，f02。f0为系统的自谐振频率，f01和f02分布在f0两边，f01小于f0，f0大于f0。

2）当耦合系数k12较大时，效率在f0附近达到最高，而f01和f02对应的效率较低；随着耦合系数k12的增大，分裂的三个频率f01，f0，f02相距越来越远。

3）当耦合系数k12较小时，同样存在三个分裂的频率，f01和f02对应的效率较高于f0对应的效率，而在f0处的效率是三个极大值中的最小值。

4）对于耦合系数k12、k23和k34，效率的频率分裂现象相似。

3 耦合特性分析

根据式（5），耦合系数是影响传输效率的关键参数，在设计过程中，只有合理选择了耦合系数才能保证系统高效率地工作。根据前文建立的效率模型，下面依次分析相邻耦合系数k12、k23和k34对效率的影响。

3.1 电源线圈与发射线圈之间的耦合系数k12 对传输效率的影响

根据效率的表达式（5），将传输效率对k12求导，得到导数如式（6）所示

在Matlab 上对式（6）进行仿真，工作频率为379kHz，k23=0.5，k34=0.2 的仿真结果如图3所示，图3中曲线与图2（a）一致。从仿真结果可以看到，效率对k12的导数始终为正，即k12越大，效率越高。

图3 ∂η/∂k12 随k12 的变化趋势

3.2 发射线圈与接收线圈之间的耦合系数k23 对传输效率的影响

根据式（5），将传输效率对k23求导，得到导数如式（7）所示

令式（7）等于零，得

当k23小于式（8）的值时，∂η/∂k23为正；当k23大于式（8）的值时，∂η/∂k23为负，那么满足式（8）时的k23可使效率最高。

在Matlab 上对式（7）进行仿真，工作频率为379kHz，k12=0.6，k34=0.2 的仿真结果如下图4所示，其中实线为效率的导数，虚线表示纵坐标为零，两线交点即为导数为零的点。图4中曲线与图2（b）一致。从图4可以看到，k23＜0.245 时，∂η/∂k23大于零；k23＞0.245，∂η/∂k23小于零，那么0.245 是最 佳的耦合系数k23。

图4 ∂η/∂k23 随k23 的变化趋势

当k23在大于0.245 的范围内增大时，效率只是稍有降低，变化不是很明显。从能量损耗的角度不难理解这一现象，因为距离的增大使系统的谐振频率稍有偏移，而谐振频率的偏移将会使发射线圈波形失真，处于失调的状态，接收线圈内阻和寄生电阻会造成功率损失，从而使效率降低[7]。发射线圈与接收线圈之间的距离d23是系统的有效传输距离，d23越大，k23越小。在实际应用中，应根据系统应用的场合设定传输距离，如果对系统的传输距离要求较低，而对效率要求高，那么可以缩短传输距离以提高效率。如果要求较远的传输距离，那么就要牺牲系统的效率来满足传输距离的要求。

3.3 接收线圈与负载线圈之间的耦合系数k34 对传输效率的影响

根据式（5），将传输效率对k34求导，得到导数如式（9）所示

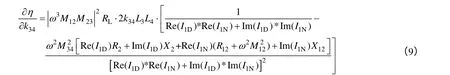
令式（9）等于零，得到

当k34小于式（10）的值时，∂η/∂k34为正；当k34大于式（10）的值时，∂η/∂k34为负，那么满足式（10）时的k34可使效率最高。

在Matlab 上对式（9）进行仿真，工作频率为379kHz，k12=0.6，k23=0.5 的仿真结果如下图5所示，其中实线为效率的导数，虚线表示纵坐标为零，两线交点即为导数为零的点。图5中曲线与图2（c）一致。从图5可以看到，当k34＜0.415 时，∂η/∂k34大于零；k34＞0.415 时，∂η/∂k34小于零，那么当接收线圈与负载线圈之间的耦合系数k34约为0.415时，效率最高。

4 系统设计与结果分析

为了验证上文建立的新型四线圈系统的效率模型，对四个谐振线圈之间的距离进行研究，设计了一种双线圈结构的WPT 系统，具体步骤如下所述。

图5 ∂η/∂k34 随k34 的变化趋势

4.1 谐振线圈间最佳距离的设计

本文的平面型螺旋线圈采用200 股漆包线的励兹线，每股漆包线直径为 0.1mm。线圈电感值为80μH，外半径为20cm，内半径为17.5cm，匝数N=10，每匝之间紧密缠绕，平均半径为18.8cm。四个谐振线圈的绕线方式、尺寸、线圈匝数、电感值、和寄生参数均相同，四个谐振电容均为2.2nF。

在设计四个线圈的相对距离之前，需要测试出本实验的两个相邻谐振线圈之间不同距离下的耦合系数k。当两个线圈的距离d一定时，互感M为常数，由伏安法可测得两个线圈之间的互感[8]，进而可得耦合系数k，测试结果如图6所示。

图6 不同距离对应的耦合系数

1）电源线圈与发射线圈之间的距离d12

电源线圈与发射线圈之间的耦合系数k12越大越好，那么这两个线圈之间的距离越小越好。那么将电源线圈与发射线圈用双线并绕的方式，绕制为一个双线圈，可以最大程度地缩短两个线圈之间的距离，增大其耦合系数。所用的两股励兹线的长度和绕制方式完全相同。两股励兹线相互独立，其中一股作为电源线圈连接在电源谐振回路中，另外一股作为发射线圈连接在发射谐振回路中，如图7所示。

2）发射线圈与接收线圈之间的距离d23

图8为本设计的效率随耦合系数k23的变化趋势。从图中可以看出，当k23=0.5（d23=6.5cm）时效率对k23的导数为零，即系统的效率最高。发射线圈与接收线圈之间的相对距离d23是WPT 系统的有效传输距离，而系统的有效传输距离要根据实际应用来确定，通常情况下是固定不变的。

图7 电源线圈与发射线圈构成的双线圈结构

图8 本设计的效率随耦合系数k23 的变化趋势

3）接收线圈与负载线圈之间的距离d34

效率随接收线圈和负载线圈之间的耦合系数k34的变化是非单调的，随着k34的增大，效率先增大后变小，存在一个最佳的耦合系数k34，可使效率达到最高。计算可得最佳的耦合系数k34为0.415，根据图6的测试结果，两线圈最佳距离约为8cm。

本设计的实验平台如图9所示，谐振线圈用透明有机玻璃板支撑，最左边是负载线圈，中间为接收线圈，最右边为包含电源线圈和发射线圈的双线圈，负载为LED 灯。

图9 系统实验装置

4.2 测试结果与分析

图10 不同d23 下的效率仿真

电源线圈与接收线圈采用双线圈结构，且k34为0.415 时，在不同d23下效率的仿真结果如图10所示，图10（a）至（d）分别为d23=10cm（k23=0.41）、d23=20cm（k23=0.19）、d23=30cm（k23=0.09）、d23=40cm（k23=0.046）时，效率随工作频率的变化。不同d23下效率的三个极大值对应的三个分裂频率f01、f0、f02依次标注在对应的图示中。不同d23情况下效率的测试结果如图11所示，x轴为工作频率，y轴为效率。图11中四条曲线对应的传输距离d23分别为10cm、20cm、30cm 和40cm。从图11中可以看到，当d23=10cm 时，随着工作频率的增大，效率出现了频率分裂现象，工作频率在f0=379kHz 附近时效率为80%，此时效率最高，与图10（a）的仿真结果一致；当d23=20cm 时，随着工作频率的增大，效率也出现了频率分裂现象，效率在f01=300kHz 和f0=379kHz附近获得极大值，且f0对应的效率较高，与图10（b）的仿真结果一致；d23=10cm 和d23=20cm 时，耦合系数较大，f01、f0、f02相距较远，最大的分裂频率f02超出500kHz 的范围，在小于500kHz 的频率范围只能看到两个效率极大值点。当d23=30cm 和d23=40cm时，由于耦合系数k23比较小，在整个频率范围内，效率始终很低；三个分裂频率相差较小，故可观察到在小于500kHz 的频率范围效率存在两个极小值点，且f02附近对应的效率高于f0和f01附近对应的效率，与图10（c）和（d）的仿真结果一致。

图11 不同距离不同频率下的效率

下面分析当k23固定为0.5（d23固定为6.5cm）时，不同d12和d34情况下的效率，测试结果如图12所示。图12（a）为d12=0cm（双线圈结构）、d12=5cm（k12=0.54）和d12=15cm（k12=0.29）时效率随工作效率的变化。图12（b）为d34=0cm（k34=0.6）、d34=8cm 工作效率的变化。从图12中曲线可以看出，采（k34=0.415）和d34=15cm（k34=0.29）时效率随用双线圈结构，以及最佳耦合系数k34的情况下，效率最高。另外，在最佳耦合系数k12和k34时，随着工作频率的变化，效率较为平稳，系统的稳定性更强。

图12 最佳耦合系数与非最佳耦合系数的效率对比

5 结论

建立了新型四线圈系统的效率模型，对系统的频率特性与耦合特性进行了研究，并分析了效率的频率分裂现象。通过分析相邻两线圈之间的耦合系统k12、k23、k34对效率的影响，找到了四个谐振线圈之间最佳的耦合系数。利用伏安法测试了两个谐振线圈之间的耦合系数与距离之间的对应关系，完成了四个谐振线圈的相对距离设计。用励兹线绕制了四个平面型螺旋线圈，提出了包含电源线圈和发射线圈的双线圈结构的设计方法，增强了系统的稳定性，改善了系统的效率和传输距离；最后，建立了新型四线圈结构无线能量传输的硬件系统，在不同工作频率和不同距离下对系统的效率进行了测试与分析，实验结果证明了理论研究的正确性。

[1] 姜燕,黄禹,李中启,等.三线圈磁谐振式无线输电系统传输效率的优化[J].电力电子技术,2014,48(12): 75-77.

[2] Niu Wq,Chu Jx,Gu W,et al.Exact analysis of frequency splitting phenomena of contactless power transfer systems[J].Circuits and Systems I: Regular Papers,IEEE Transactions on,2013,60(6): 1670-1677.

[3] Zhang Yiming,Zhao Zhengming.Frequency splitting analysis of Two-Coil resonant wireless power transfer[J].IEEE Antennas and Wireless Propagation Letters,2014,13: 400-402.

[4] Chen Kainan,Zhao Zhengming,Zhang Yiming,et al.Analysis of structure and parameters in wireless power transmission system with consideration of losses in source[C]//2013 TWENTY-EIGHTH ANNUAL IEEE APPLIED POWER ELECTRONICS CONFERENCE AND EXPOSITION (APEC 2013),2013: 2575-2581.

[5] Sample AP,Meyer DA,Smith JR.Analysis,experi- mental results,and range adaptation of magnetically coupled resonators for wireless power transfer[J].IEEE Transactions on Industrial Electronics,2011,58(2): 544-554.

[6] Ahn D,Hong S.A transmitter or a receiver consisting of two strongly coupled resonators for enhanced resonant coupling in wireless power transfer[J].Indus- trial Electronics,IEEE Transactions on,2014,61(3): 1193-1203.

[7] Wang Q,Li H.Research on the wireless power transmission system based on coupled magnetic reson- ances[C].Electronics,Communications and Control (ICECC),2011 International Conference on.IEEE,2011: 2255-2258.

[8] 王素姣.磁耦合线圈互感系数M 的测量[J].郑州铁路职业技术学院学报,2002,14(2): 43-44.