基于优化PID的食品加工恒温控制研究

李 勇

（重庆港渝商业管理公司，重庆 400010）

随着人们对健康意识的不断提高，国家对食品质量的要求也越来越严格。在食品加工行业，利用恒温控制技术能够使食品质量在加工的环节中得到最大限度的保持，降低了食品腐败率[1]。在进行食品加工的环节中，由于温度的控制系统是一个存在滞后性和时变性的系统，因此，如何在食品加工过程中进行恒温控制，已经成为当前工控领域的一个热点研究课题。传统的食品加工过程中恒温控制方法是通过常规的PID 控制方法实现的。PID 控制器具有简单可靠、易于实现、适应性强等特点，是食品加工行业中使用最普遍的一种恒温控制方法。但是这种方法应用于存在滞后性和时变性的食品加工恒温控制系统时无法实现理想的控制效果。

因此，针对常规的PID 控制算法在食品加工过程中存在的缺陷，有必要进行优化。现阶段已经有很多专家针对这种缺陷提出了独特的见解。当前主要的食品加工过程中的恒温控制方法主要有基于积分分离的PID 控制方法、基于参数自整定的PID 控制方法和基于不完全微分的PID 控制方法。其中，基于积分分离的PID 控制方法是在食品加工行业应用最广泛的一种恒温控制方法。由于食品加工过程中的恒温控制方法在保障食品质量方面具有无可替代的作用，因此拥有广阔的发展前景，并被很多学者作为重点课题进行研究。

1 恒温控制软件设计原理

传统的食品加工过程中恒温控制的有关原理如下所述。

在进行食品加工过程中恒温控制的过程中，通过控制偏差对温度进行调节，从而使食品加工过程中的温度维持在一定的范围内。PID 控制的核心是，将当前温度与目标温度相比较得到温度偏差，并将温度偏差转化为电压信号的形式，利用电压信号对供热系统进行调节，从而实现了食品加工过程中的温度控制。恒温控制的关键是利用控制过程中的温度偏差产生电压信号，将电压信号进行比例、微分、积分化，产生控制信号。图1所示描述了食品加工过程中的恒温控制器的结构。

图1 传统的恒温控制结构

在食品加工过程中恒温控制的过程中，将温度偏差转化为PID 的比例、微分和积分化的电压信号组合[1]，将供热系统的实际值作为PID 控制器的输入值，食品加工过程中的温度调节过程能够用下述公式进行描述：

式中，U(t)为供热系统的实际值；e(t)为调节温度的信号；Kp、TI和Td分别为比例系数、微分时间参数和积分时间参数[2]。

将公式（1）进行离散化处理，能够转换为差分方程的形式：

在进行食品加工过程中恒温控制的过程中，需要确定合理的调节参数，并及时对控制参数进行调整，从而实现满意的温度控制效果。调节参数的确定过程如下所述：

1）设置积分系数Ki=0 和微分系数Kd=0，此时恒温控制系统工作在闭环状态下，利用比例系数Kp调节温度信号，并对温度控制效果进行监测，直至达到理想的控制效果。

2）不断对比例系数Kp进行调整，并增大积分系数Ki的值，直至满足实际控制要求。

3）在积分系数Ki的值一定的情况下，按照从小到大的方式调节比例系数Kp的值，并对温度控制效果进行监测，直至达到理想的控制效果。否则，对比例系数Kp和积分系数Ki的值进行不断的调整，直至得到合理的Kp值和Ki值。

4）在控制参数的调整过程中引入合理的微分时间参数TI和积分时间参数TD，并不断调整比例系数Kp和积分系数Ki的值，直至满足实际控制要求。

根据上述方法，在食品加工过程恒温控制的过程中不断调节控制参数，并不断实验。当Ki=0.03，Kd=12 时，能够得到理想的温度控制效果，此时，控制过程需要的时间为33s，超调量为0.96%。图2所示描述了食品加工过程中的温度调节效果。

图2 传统算法恒温控制效果

2 基于优化PID 的恒温控制方法

2.1 控制参数的确定过程

在进行食品加工过程中恒温控制过程中，需要通过BP 神经网络获得温度控制过程中的相关参数。设置温度控制误差为f(l)，利用下述公式能够对输入的温度调节信号进行归一化处理：

利用下述公式能够计算食品加工过程中环境的温度变化率：

设置食品加工过程中恒温控制的误差为F，PID 的控制参数为LQ、LM和LE，由于这些参数的数值都大于0，因此，BP 神经网络的输出也大于0。图3所示描述的是本文用于PID 参数优化的神经网络结构。

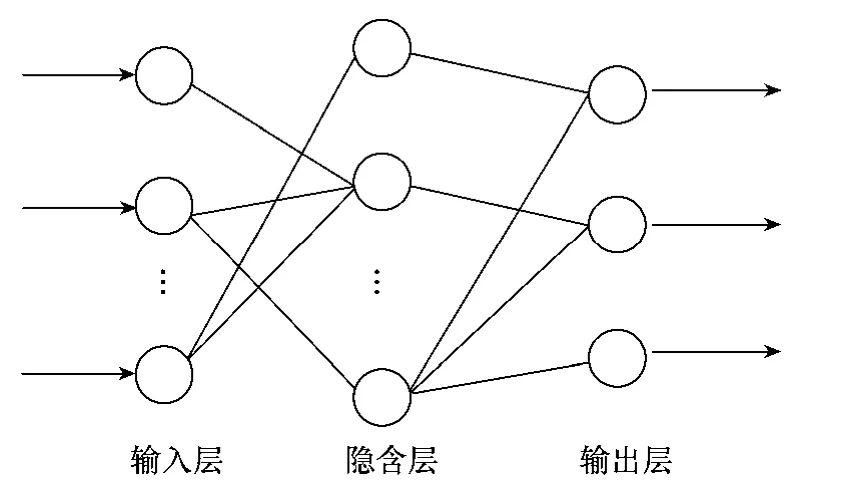
图3 BP 神经网络结构

利用下述公式能够描述温度调节信号的输入量：

式中，N为温度调节信号的数目，是根据食品加工过程中的温度变化情况获得的。

BP 神经网络隐含层的输出量能够用下述公式进行计算：

BP 神经网络的输出量能够用下述公式进行计算：

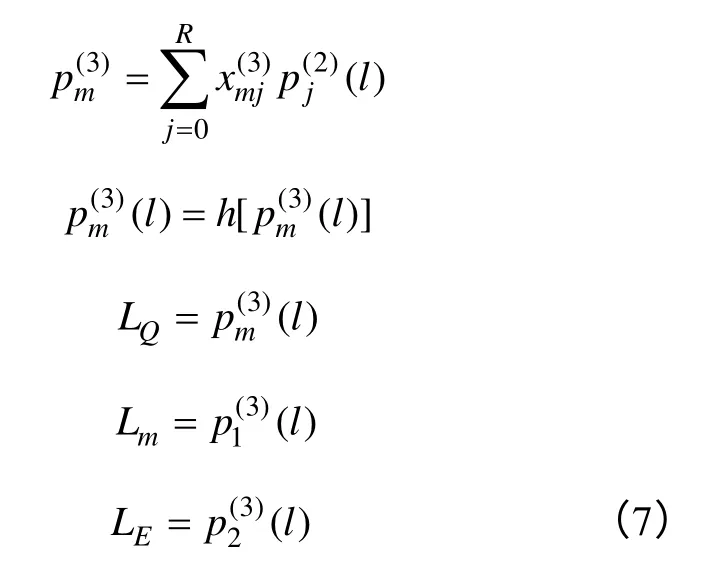
根据上述方法，能够利用BP 神经网络能够获得PID 的控制参数，并作为食品加工过程中的恒温控制初始参数。

2.2 食品加工过程中恒温控制的实现

经过BP 神经网络优化后的参数作为PID 控制器的初始参数，对食品加工过程中的温度进行调节，具体方法如下所述：

利用下述公式能够描述食品加工过程中的温度变化情况：

在BP 神经网络中引入梯度下降法[3]，对各层的连接权重进行更新，其公式如下所述：

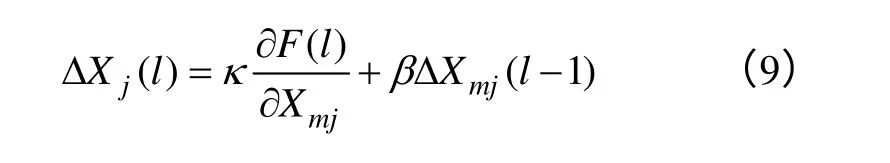
式中，κ为食品恒温控制过程中的参数更新速度，β是其系数。

利用下述公式能够计算恒温控制过程中温度误差：

利用下述公式能够获得反馈至控制端的恒温控制参数：

通过式（11）能够获得准确的恒温控制参数，从而实现对温度的实时调节。

食品加工过程中的恒温控制具体过程如下所述：

1）构建BP 神经网络模型，确定模型的结构、响应的连接权重和阀值[4]；PID 的控制参数通过构建的BP 神经网络进行优化。

2）计算模型的输入量与输出量的之间的差值，其公式如下所述：

3）计算PID 控制器的参数和反馈调节参数，利用反馈参数对温度控制参数调整；

4）设置l=l+ 1，并跳转到过程2）。

根据上面阐述的方法，PID 控制参数通过BP神经网络模型进行优化，并作为PID 的初始参数，计算反馈参数，将当前食品加工过程中的温度变化情况反馈到PID 输入端进行温度调节，从而实现了食品加工过程中的恒温控制。

3 实验结果及分析

3.1 实验参数设置

为了验证本文算法在食品加工过程中恒温控制方面的有效性，需要进行一次仿真实验。利用传统的PID 控制方法与本文优化的PID 控制方法进行对比。本文的食品加工过程中的恒温控制系统能够用图4进行描述。

图4 本文的恒温控制系统

在上图4中，Ir为温度预警值，Qa为当前温度，Q为超温值，Wa1(s)为PID 的主调节器，Wa2(s)为PID 的从调节器，Wo1(s)为调节阶段的控制函数，Wo2(s)为非调节阶段的控制函数，WH1(s)为调节阶段的检测值，WH2(s)为非调节阶段的检测值，d1为调节阶段的扰动值，d2为非调节阶段的扰动值。

设置主、从调节器中的参数为

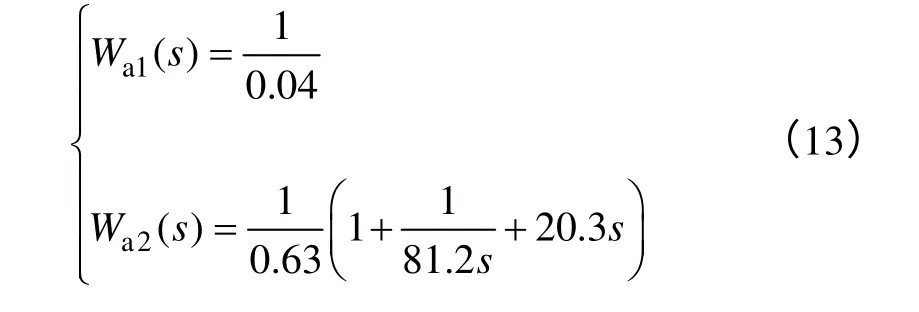
其他参数设置为：η1= 0.3，K1= 1.12，η2= 0.6，K2= 1.4。

3.2 不同算法结果比较与分析

在进行食品加工过程中恒温控制的过程中，利用传统算法和本文算法进行实验，获得的结果能够用图5进行描述。

从上图5能够可以看出，本文算法在食品加工过程中环境温度变化程度较大的情况下仍能保持良好的输出效果，而传统算法在工况出现变化时，超调量更大，控制效果降低，这表明本文算法具有调节时间快、抗干扰性能强等特点。

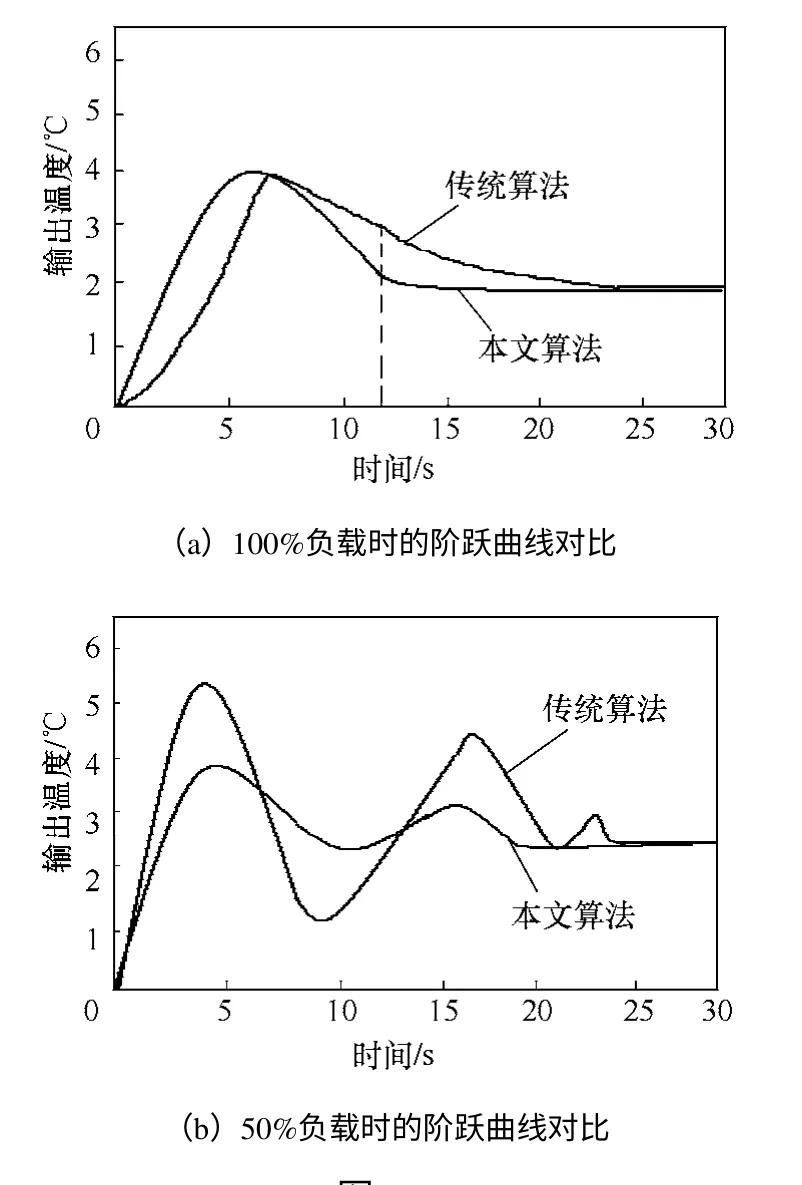
图5

为了进一步验证本文算法的优越性，利用不同算法对食品加工厂中恒温控制系统多次实践，并通过在计算机上编程获得传统算法和本文算法的恒温控制曲线，如图6所示。

图6 控制曲线

从图6中的实验结果可以看出，本文算法的恒温控制系统对于食品加工过程中的温度变化调节的平稳性相对传统算法有了明显的提高，主要表现在食品加工过程中的温度上升和温度下降时的调节过程更加平滑和稳定，避免了传统算法进行恒温控制时的温度跳跃式升高或者下降的现象。这是由于本文算法利用神经网络对PID 的控制参数进行了优化，并作为PID 的初始参数，通过计算反馈参数，将当前食品加工过程中的温度变化情况反馈到PID输入端进行温度调节，从而实现了食品加工过程中的恒温控制的理想效果。将上述实验中的数据进行整理和分析，能够得到表1中的数据。

表1 不同算法恒温控制效果比较

从表1中实验数据能够得知，利用本文算法进行食品加工过程中的恒温控制，能够取得理想的温度调节效果，相对传统算法有着较强的优势。

4 结论

本文提出一种基于优化PID 的恒温控制方法。构建BP 神经网络模型，利用该模型对PID 的控制参数进行优化，获得最优初始的PID 控制参数，在恒温控制的过程中，计算反馈调节参数，将当前食品加工过程中的温度变化情况反馈到PID 输入端进行温度调节，从而实现了食品加工过程中的恒温控制。仿真实验结果表明，利用本文算法进行食品加工过程中的恒温控制，降低控制过程中的超调量，缩短控制时间，取得了令人满意的效果。

[1] 李草苍,张翠芳.基于最小资源分配网络的自适应PID 控制[J].计算机应用研究,2015,32(1): 167-169,178.

[2] 孙大鹰,徐申,孙伟锋,等.Buck 型DC-DC 变换器中数字预测模糊PID 控制器的设计与实现[J].东南大学学报(自然科学版),2014,44(5): 897-901.

[3] 邓小东,赵宇宏.针对可变柔性负载的参数自整定模糊PID 控制算法的仿真研究[J].机械制造,2014,52(10): 9-11.

[4] 赵秋宇,胡万强.CMAC-PID 控制器在提升装置速度控制中的应用研究[J].许昌学院学报,2014,33(5): 50-52.