基于纵向阻抗的输电线路故障测距研究

李江川 王 勇 周利兵 张 东

（1.国网新疆电力公司福海县供电公司，新疆 福海 836400； 2.国网新疆电力公司电力科学研究院，乌鲁木齐 830011）

随着超/特高压电网建设的快速进行，线路出现故障的机率也随之增大。在线路出现故障后，及时查找故障位置，协助分析线路故障原因并采取相对应的措施，减少电网因输电线路故障而造成的损失成为一个亟待解决的问题。随着研究的深入，线路故障测距的理论[1-7]和方法也有了新的发展，从以前的单端测量发展到现有利用光纤的双端测量。由于双端测量[8-9]具有不受过渡电阻的影响的特点而倍受欢迎，但现在的双端量测量多采用分布参数的线路模型[10]，但由于其计算复杂，在线测量实现困难。本文基于纵向阻抗推导出一种双端量故障测距公式，分析系统解耦、故障类型及过渡电阻等对测距公式的影响[11]，发现这些因素对测距公式计算结果的影响不大，最后通过仿真验证了本文公式的正 确性。

1 纵向阻抗的特性分析

1.1 单相线路模型下的纵向阻抗

根据文献[12]所赋纵向阻抗的定义，已经获得纵向阻抗在单相模型下的计算表达式为

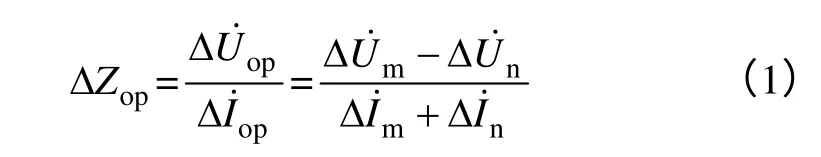
在进行纵向阻抗幅值保护时，上式应加绝对值，如式（2）所示。

当保护区外发生故障时，如图1（a）所示，其纵向阻抗幅值的判别式如式（3）所示。

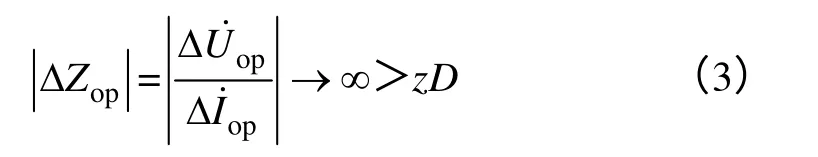
图1 R-L 单相等效工频故障分量的线路模型

从上式可以看出，保护区外发生故障时，纵向阻抗的幅值将趋于无穷大；在任何方式下外部故障时纵向阻抗的幅值都会大于线路阻抗。但当保护区外发生故障时，如图1（b）所示，纵向阻抗幅值的判别式如下式所示。

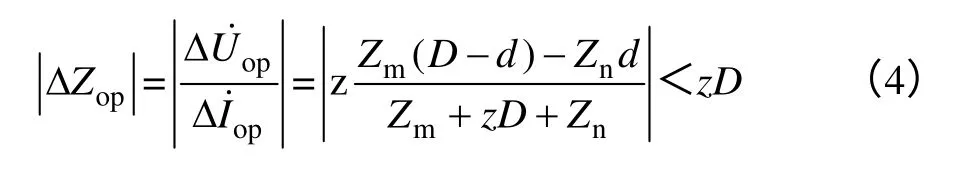
从上式可以看出，保护区内发生故障时，纵向阻抗幅值会小于线路阻抗。同时从上式也可以看出，纵向阻抗幅值与故障距离成线性关系。

1.2 三相线路模型下的纵向阻抗

单相接地故障时，三相等效工频分量线路模型如图2所示，零序等效工频线路模型如图3所示。

图2 a 相单相接地故障下的R-L 三相等效 工频故障故障分量的线路模型

图3 零序等效工频线路模型

图2是a 相单相接地故障下的R-L 三相等效工频分量的线路模型，图3是零序等效工频线路模型。图中所示各项参数请参阅文献[4]。

从上图可以看出，线路两端的每相电压故障分量的相量差如下式所示

由图3可以看出，故障时零序电压和零序电流的关系可以用下式表达：

将式（5）中的零序电流相关项用式（6）中的零序电压进行等效替换，可得

根据式（7），在图2中消除相间耦合后得到单相等效工频故障分量模型如图4所示。

图4 通用的单相等效工频故障分量线路模型

同时从式7 可以看出，三相线路解耦后被保护线路内部参数与单相线路参数一致。由此可得线路纵向阻抗表达式如式（8）所示。

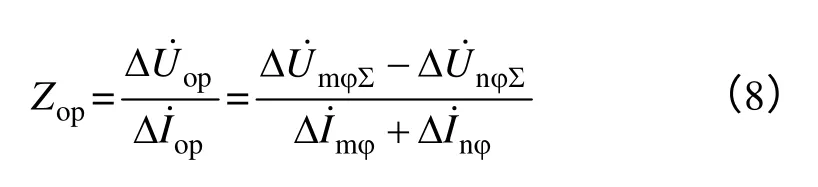
2 测距算法

2.1 单相模型下的测距算法

由前面的分析可知，纵向阻抗幅值与故障距离成线性关系，将利用纵向阻抗表达故障距离如式（9）所示。

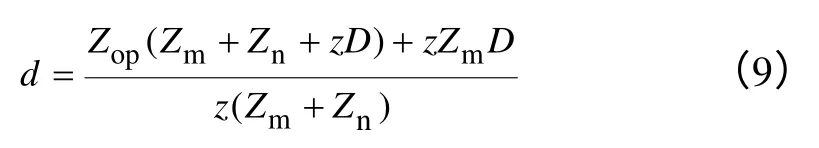
2.2 三相模型下的测距算法

根据前面分析的三相模型解耦后等效为单相模型纵向阻抗模型，可以求得三相线路解耦后的纵相阻抗表达式如式（10）所示。

根据式（10）解得故障距离与纵向阻抗的关系如式（11）所示。

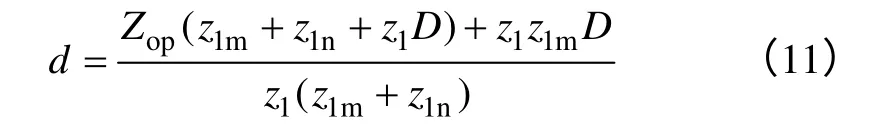
在上面的分析中，推导纵向阻抗时没有考虑系统阻抗解耦，在考虑系统阻抗解耦后，纵向阻抗的幅值和相角可能会产生一定的变化，下面分析系统阻抗角耦对纵向阻抗的影响。

2.3 系统阻抗解耦对测距的影响

如图2所示，线路故障时，发生故障线路两端的电压和电流分量用保护区外的系统阻抗来表达的表达式如式（12）、式（13）所示。

同理，如图3所，故障时零序电压和零序电流用保护区外的系统阻抗来表达的表达式如下式所示。

根据图3零序电压和零序电流用区外系统阻抗表示的关系式为

整理式（12）和式（13）可得

式中

根据式（7）和式（9）可得

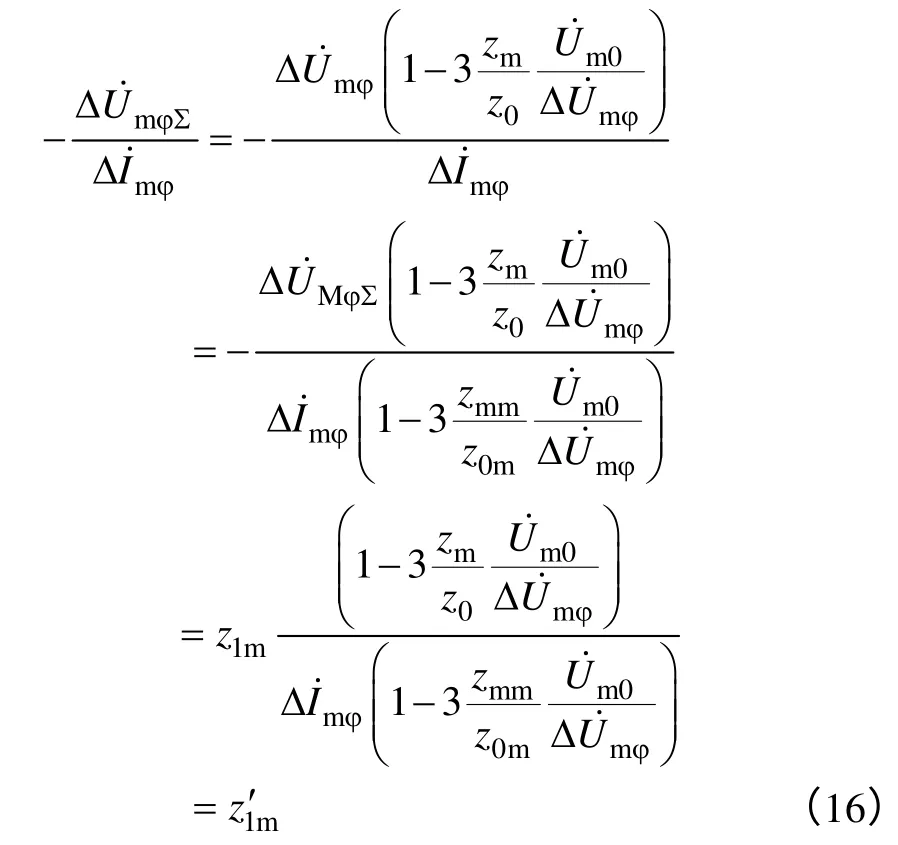
同理

由式（16）和式（17）可以看出，线路发生故障时保护区外的等效系统正阻抗分别为Z1′m、Z1′n。但在/特高压输电线路中所有相关阻抗的相角都非常接近90°，因此，保护区外阻抗相角不会发生明显变化。同时从式（16）和式（17）中可以看出，测距结果基本上不受系统阻抗解耦的影响，所以系统阻抗解耦基本上不会影响故障测距的精度。

3 仿真结果及其分析

3.1 仿真模型搭建

利用EMTP 建立仿真模型，在EMTP 中根据750kV 沙洲至哈密输电线路实际运行参数搭建了简化的分布参数电路模型。线路长度235.8km，输送功率1300MW，电源频率50Hz，两个变电站的电源电势分别为EMs = 673528∠ 0°，ENs = 612298∠ - 50°，量纲为伏特，线路参数正序电阻0.0162Ω/km，正序电抗0.2824Ω/km，零序电阻0.2082Ω/km，零序电抗0.8946Ω/km。

3.2 仿真与分析

仿真采用EMTP 得出故障前后的电流电压数据，然后利用上面分析的故障距离计算方式对故障距离进行计算，然后根据设置的故障距离与计算得到的故障距离相比得出计算误差。

仿真结果统计如下，表1为不考虑过渡电阻时仿真设置的故障距离和故障计算距离的结果，表2为考虑过渡电阻时仿真设置的故障距离和故障计算距离结果见表1，设置的故障距离与计算的故障距离最小相对误差为3.4%，最大相对误差为4.6%，由此也验证了该法在不考虑过渡电阻时的正确性。从表2可以看出，考虑过渡电阻时设置的故障距离与计算的故障距离最小相对误差为2.1%，最大相对误差为2.9%。对比表1和表2的计算结果可知，该算 法基本不受过渡电阻的影响。

表1 不同故障点时不同故障类型下的测距结果

表2 a 相单相接地下不同故障点时不同过渡 电阻下的测距

4 结论

本文利用纵向阻抗的优良性及线路解耦后等效故障模型，推导出不同情况下故障的距离公式，在公式推导后分析了系统解耦对故障测距的影响，分析结果表明系统解耦对指导出的故障距离计算公式影响不大。然后利用EMTP 对750kV 沙洲至哈密输电线路进行了设置不同接地故障后的仿真分析，从仿真得到的电流电压参数利用本文推导的公式计算出故障距离与设置的故障距离相比较，比较结果验证了本文推导的故障距离计算公式的具有较高的准确度且不受故障类型的影响，同时也仿真分析了过渡电阻对本文推导公式的影响，仿真分析结果表明过渡电阻几乎不对本文推导的公式造成影响。

[1] 葛耀中.新型继电保护和故障测距的原理与技术[M].西安: 西安交通大学出版社,2007: 256-333.

[2] 邬林勇.利用故障行波固有频率的单端行波故障测距法[D].成都: 西南交通大学,2009.

[3] 王志华.超高压线路故障行波定位及高压变频技术研究[D].武汉: 华中科技大学,2004.

[4] 宋国兵,蔡新雷,高淑萍,等.高压直流输电线路故障定位研究综述[J].电力系统保护与控制,2012,40(5): 133-137,147.

[5] 杨淑英,袁宝.基于反向行波的小电流接地系统故障定位[J].电力科学与工程,2011,27(6): 28-32.

[6] 郭安明,钟俊,王永洪,等.基于复小波的输电线路行波三端测距算法[J].电力系统保护与控制,2012,40(7): 100-104,111.

[7] 徐岩,张锐,霍福广,等.基于MAS 信息融合的电网故障诊断[J].电力科学与工程,2012,28(9): 24-28.

[8] 范新桥,朱永利.基于双端行波原理的多端输电线路故障定位新方法[J].电网技术,2013,37(1): 261-269.

[9] 李配配,黄家栋.配电网混合线路双端行波故障测距方法的研究[J].电力科学与工程,2011,27(11): 31-34.

[10] 林湘宁,黄小波,翁汉琍,等.基于分布参数模型的比相式单相故障单端测距算法[J].电网技术,2007,31(9): 74-79.

[11] 夏经德.索南加乐,王莉.基于输电线路纵向阻抗纵联保护新原理的研究[J].电力系统保护与控制,2011,39(4): 43-51.