《代数学》和《代数术》传入我国的无穷级数收敛问题

王红杉，郭世荣

（内蒙古师范大学 科学技术史研究院，内蒙古 呼和浩特 010020）

在无穷级数研究史上，18世纪的数学家并不关注级数的收敛与发散问题。进入19世纪，无穷级数的收敛问题开始受到傅里叶（Joseph Fourier，1768—1830）、高斯（Carl Friedrich Gauss，1777—1855）、波尔查诺（Bernard Bolzano，1781—1848）等数学家的重视。1811年，傅里叶在其《热的解析理论》中给出了级数收敛的满意的定义，接着一批数学家研究了收敛的判别准则等[1]。清代中期的数学家遇到了级数收敛的问题。如明安图在其著作《割圆密率解法》中遇到了用级数计算“降位”迟速的问题，实际上就是收敛速度快慢的问题，其后研究无穷级数的中算家都遇到了同样的问题。此时，中算家就采取换用其他级数的办法来解决“降位”太慢的问题。“由于中算家对级数收敛性缺乏分析的讨论……不过中算家未必认识到它们对级数的收敛性要求。”[2]1859年出版的译著《代数学》首次向中算家介绍了级数收敛的概念及其判别方法，1873年出版的译著《代数术》也有简略涉及。受《代数学》和《代数术》的影响，中国数学家开始对级数的收敛问题有了一定的认识，并应用于研究中。本文首先介绍《代数学》和《代数术》传入我国的级数收敛内容，然后以长沙学派为例说明中算家的回应。

1 《代数学》中传入我国的级数收敛问题

19世纪中期以后，有4部译著涉及到无穷级数问题，它们是伟烈亚力（Alexander Wylie,1815—1887）与李善兰（1811—1882）合译的《代数学》13卷（1859）和《代微积拾级》18卷（1859），及傅兰雅(John Fryer，1839—1928)与华蘅芳(1833—1902)合译的《代数术》25卷（1873）和《微积溯源》8卷（1874）。其中，《代微积拾级》和《微积溯源》中用到了与级数相关的知识，但并没有明确给出级数定义及讨论级数收敛问题。《代数学》[3]卷八首次介绍了与级数收敛有关的内容，主要包括：

（1）级数收敛的概念。《代数学》卷六定义了无穷级数及无穷级数的和（称为“总数”），卷八“论级数及未定系数”首先给出级数收敛与发散的概念：

界说：无穷级数之总数，即诸级递加递进之限。若有此限，则谓之敛级数，任并其诸级，不能得大于限之数。若无此限，则谓之发级数也。[3]卷八，1

这里的“敛”和“发”今日用双字“收敛”和“发散”。注意到定义似乎主要是针对正项级数的，因为后面接着还有“不能得大于限之数”，这只对“递加递进”的级成立。因此这个定义还不是很严密，因为对于负项级数，其和应当“不能得小于限之数”。正项级数是递加的，因此级数的收敛与发散定义为级数各项递加之和有无上限，有则收敛，无则发散。《代数学》主要论述正项级数，但也涉及到了交错级数的收敛问题。在讨论收敛问题时，最重要的一个级数是：x＜1时，1+x+x2+x3+x4+… 为敛级数,其和为，即：

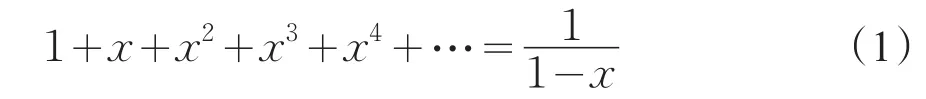
（2）级数的通项公式。接着，《代数学》指出无穷级数各项间的关系（即“连属之理”）之重要性：“凡无穷级数须明第一级与前一级相连属之理。不然，不能用以穷理。蓋其级无穷，既不能尽纪，若不知连属之理，则未纪之级不能知。所以凡无穷级数若无相连属之理，准穷理例，必无是数。”亦即：无穷级数有无穷多项（即“级”），不能一一列出，若不出通项公式，则难以确定此级数，无法进行推理。原著在这里给出了一个较难的例子：

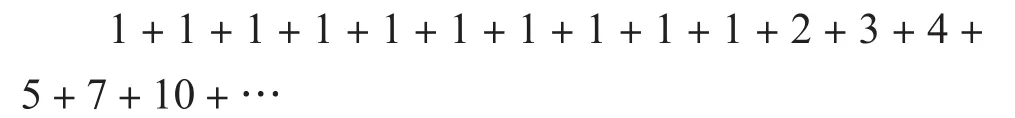
原著指出：“此无穷级数相连属之理，乃以第卯级前诸级之总数，取其十位数，加于卯级之数得（卯丄一）级之数。如此诸级之总数未至十，则级数皆同。”即：该级数的第n＋1项是它前面n项之和的十位数加上第n项之数。例如，第15项之7是这样得来的：前14项之和为24，取十位数之2，再加上第14项之5；第16项：前15项之和为31，取十位数3，再加第15项之7，得10。由此可知，第17项为14。

有了这样的铺垫，《代数学》定义了通项：“界说：凡级数之公级必为第卯级之式。”同时，也提到一个无穷级数的通项可以从有限项之后开始，即前面有限项可以不满足通项。

（3）级数收敛的判别。《代数学》给出三组无穷级数收敛或发散的判别法则。对于无穷级数：

《代数学》首先利用式（1）推导出一个判别准则。

级数（2）可变为

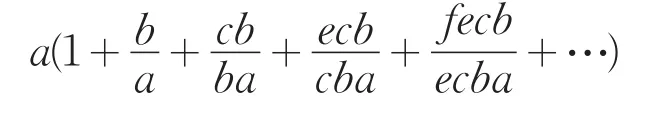
若记原级数后项与前项比分别为B、C、E、F等，则变为

若B、C、E、F等均小于一个数，比如p，则原级数

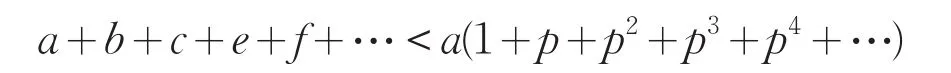
故凡级数每级与上一级之比例若更小于小于一之数，则必为敛级数。或数级之后如此，亦同。其诸级中，必有级小于任何分数，则为敛级数。[3]卷八，6

相关的，若B、C、E、F等“皆大于一，或数级之后如此，则为发级数。”[3]卷八，9

关于交错级数收敛的判别条件有，对于交错级数

若其诸级无限损，即甲大于乙，乙大于丙，以下皆如此，其诸级中必有级小于任何分数，则为敛级数。

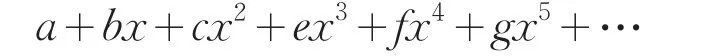
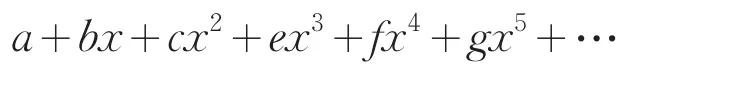
“必为发级数”。

《代数学》中还给出与收敛级数相关的一些性质，例如，对于无穷级数

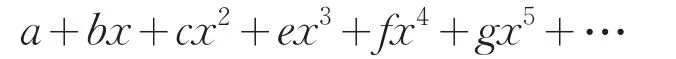
总可找到x的一个很小的值x1，使当x＜x1时，级数的某项大于其后各项之和。这相当于此级数存在一个收敛半径。又如，对于两个级数

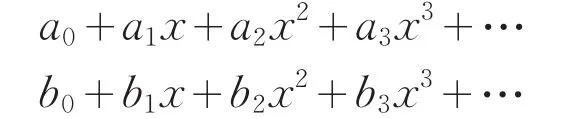
如果对于x的任意有限值都相等，那么有a0=b0，a1=b1，a2=b2，a3=b3，…

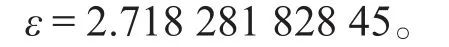
总之，《代数学》一书中在我国首次出现了级数收敛与发散的定义、判别法则和大量例子，并讨论了一些与级数收敛相关的性质。但是也应看到，该书只是对收敛与发散一个初步的讨论，内容并不多。

2 《代数术》中的收敛问题

当翻译出版《代数术》时，中国读者对收敛问题已不陌生。《代数术》中并没有涉及收敛的一般问题，但在第18和第25卷中涉及到级数的收敛速度和收敛区间等问题，书中对收敛问题的实际应用，对于中国读者很有帮助。

《代数术》卷十八“论对数与指数之式”，导出对数的级数表达式。其中第169款为：

凡以未天=地之式，而求其天之同数，则各项必以未与地明之。[4]第169款

即已知将ax=y，将其展开成用y表示x的无穷级数，经过一系列推导，得出

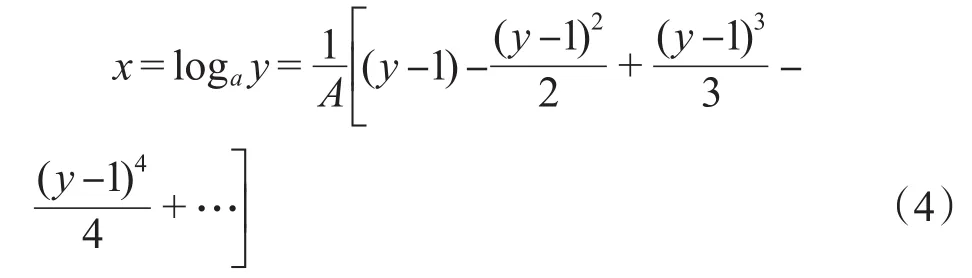
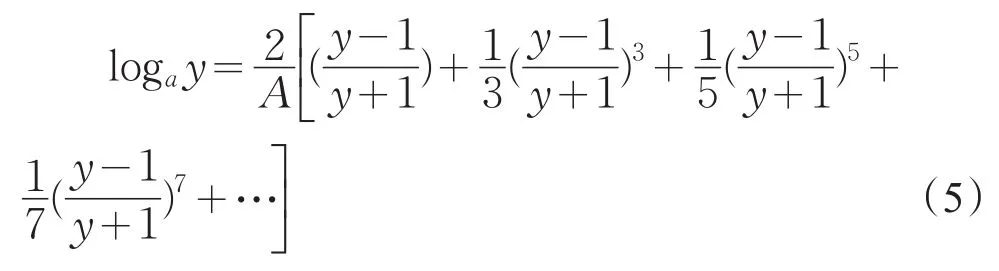
原著指出：“则地（y）之同数，无论如何，此式必为敛级数。故用此公式易推出奇零各小数之对数。”即式（5）对所有y都是收敛的。式（5）虽然收敛较快，但不是最快的，于是原著第171款又利用式（5）推出一个收敛最速的级数：设n为任一真数，其对数已知，在式（5）中令 =，可得y

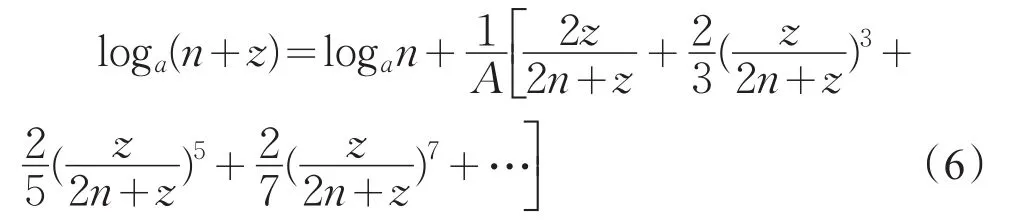
“此级数由可藉卯（n）之对数得卯丄人（n+z)之对数。如卯为大数，则级数之敛最速。”这是已知n之对数，求（n+z)之对数的一个级数，其优点在于当n较大时，收敛速度很快。

《代数术》卷25“论八线数理”也涉及到级数收敛问题。文中推出“古累固里所设之式”，即今所谓格里高里（James Gregory,1638—1675）正切求角级数展开式：

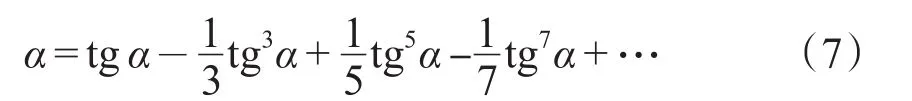
在此式中令α=45°，则得：

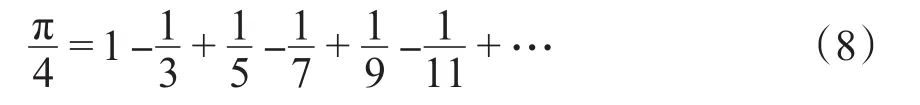
“惟此级数之敛太迟，故无大用处。”[4]第171款所以奈端（今译牛顿）又给出

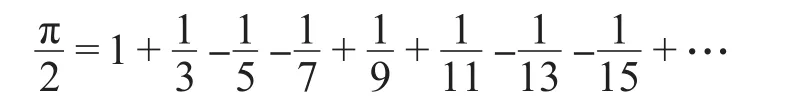
这个级数的收敛速度比上一个快，但是依然不实用：“奈端所设之级数，虽比古累固里之级数敛得较速，然奈端言，用以求象限之弧，必引长至五十万万项，方能得二十位密率。其功夫极大，若一人为之，须千年方毕，所以未为善法。”从而又转求收敛更快的级数，如利用，令 tgα=，，由，利用式（7）可得收敛更快的计算圆周率的无穷级数。又如

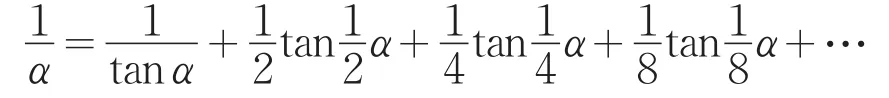
总之，《代数术》其实并无讨论无穷级数及其收敛与发散问题的专门章节，但使用无穷级数进行推理论证或导出公式的内容较为丰富。

3 无穷级数收敛问题对中算家的早期影响

上述两部译著中介绍的无穷级数知识，特别是处理收敛问题的方法，对于中国数学家来说具有重要意义，特别是《代数术》在介绍对数、三角等内容时使用无穷级数进行推导并考虑收敛速度的方法与思路，与二书传入之前中算家的研究工作有紧密关联。从明安图《割圆密率捷法》开始，无穷级数“降位”问题，即收敛速度问题，一直是研究者必须处理的问题。例如后来的戴煦（1805—1860）在其《求表捷术》《对数简法》《续对数简法》《外切密率》等著作中都为有相关的内容。如果中算家能够很好地掌握和理解《代数学》和《代数术》中的相关内容，则对于理解明安图以来的无穷级数工作颇为有益。

《代数学》出版之后，作为一门新学科，中算家需要花费一定的时间来消化和理解。因为有《代数学》为基础，当14年后《代数术》出版时，中算家的反应就显得比较迅速。其中，以丁取忠（1810—1877）为首的长沙数学学派对传入的新代数学的回应较为积极。他们很快便抓住了两部译著的内容并应用于自己的研究中，特别是吴嘉善（1820—1885）在《代数术》传入之前就颇受《代数学》影响，对新代数学颇有理解。下面，通过简要分析《对数详解》[5]（1874）和《圆率考真图解》[6]（1874）二书的相关内容来说明《代数术》对长沙学派的影响。

《代数术》出版后，立即引起长沙学派的数学家的注意和重视，开始学习和研究，正如丁取忠在《对数详解》序言中所说：“近年与曾君栗诚交，讲求天元借根之理，而尤孜孜于《代数术》一书。”在《代数术》出版后第二年，他们就在自己的研究中直接或间接地使用了《代数术》中的内容和思想，其中最为明显的是《对数详解》和《圆率考真图解》。

《对数详解》5卷，是曾纪鸿（1848—1877）的著作，但署名为丁取忠撰、黄宗宪校。该书卷首和卷一主要是作者对《代数术》中介绍的代数方法的理解和总结，作为使用新传入的代数方法的基础。卷二至卷五讨论对数，其核心内容基本上就是《代数术》卷十八中关于对数的内容，有不少几乎是照搬自《代数术》，二者的对比如表1。

表1 《对数详解》与《代数术》内容的比较

《圆率考真图解》最初也是曾纪鸿撰写的，后来左潜（？—1874）和黄宗宪分别做了补充，丁取忠在序言对此有说明。出版前，左潜突然去世，为了纪念他，出版时他的名字在作者中署在第一的位置上。这部著作的内容是通过无穷级数计算圆周率，其本思想也是来自《代数术》，在序言中丁取忠讲到了求圆周率的历史，其中提到：“西士固灵曾竭毕生之精力，只得圆率三十六位，至没时，犹令其子刻之墓碑。”[6]1就是从《代数术》中摘引来的。该书一开始就介绍了全书的主要思路：

因思以八线径求弧背眞数。而八线之整数易知者。唯九十度正弦与半径等，同为单一；三十度正弦与半径之半等，其数为〇.五；四十五度正切与半径等，同为单一。若用九十度正弦，依徐君靑术求得弧背，二因之卽半周率。若用四十五度正切，依徐氏术求得弧背，四因之卽半周率。若用三十度正弦，依徐氏术求得弧背，六因之卽半周率。三术中，唯用三十度正弦求弧背，得数较速，然欲求三四十位，则敛级亦钝。或用四十五度正切求弧背二三十位，一人为之，须数百年方可得数。所以然者，凡正切求弧背者，必以正切幂为乘率，半径幂为除率，四十五度正切卽半径，犹之不乘不除，仅有一除、三除、五除、七除诸正负数，故降位极迟也。今思变为捷术：法将四十五度正切分为二分。取其一分正切，定为二分半径之一。又用四十五度切线（与半径等）为大弧切，此二分半径之一为小弧切，用大弧切、小弧切求较弧切公式，求得较弧正切，为三分半径之一。乃先用小弧切线用较弧切线，依徐氏术求得弧背眞数，为较弧。爰将小弧、较弧两真数相倂，即四十五度弧背，四因之卽半周率，二因半周率卽全周率矣。[6]2-3

这个研究思路，是从《代数术》卷二十五的相关内容中总结和抽取出来的。所谓徐氏（有任）术，就是上节的式（7），所以《圆率考真图解》最关键的方法就是：取tgα=和tgβ=，并把正切和角公式与，依徐氏术求得弧背眞数，为小弧。再式（7）相结合。

总之，《代数学》和《代数术》二书向中国学者介绍了无穷级数收敛的基本内容，提供了一些算例。长沙学派的数学家对这两部代数学著作的反应是快速和积极的，他们认识到了新代数学的先进性，并积极地应用于自己的研究中，这从个方面说明二书出版之初对中算家的影响情况。同时也须说明，丁取忠等人引用和参考了两部译著，但是并没有很好地说明其工作与新译著的关系，相反，他们尽量从中算家的已有工作为自己的工作寻找基础与来源。例如，在《圆率考真图解》在简述相关研究历史时，根本没有提到《代数术》。

[1]克莱因.古今数学思想：第4册[M].上海：上海科学技术出版社，2012：19-25.

[2]特古斯.清代级数论基础[J].内蒙古师大学报：自然科学汉文版，1998，27（3）：78-85.

[3]棣么甘.代数学[M].李善兰，伟烈亚力，译.江夏：程氏，1898.

[4]华里司.代数术[M].华蘅芳，傅兰雅，译.上海：慎记书莊，1874.

[5]丁取忠.对数详解[M]//丁取忠.白芙堂算学丛书.上海：鸿文书局，1898.

[6]左潜，曾纪鸿，黄宗宪.圆率考真图解[M]//丁取忠.白芙堂算学丛书.上海：鸿文书局，1898.