温度梯度作用下非饱和土壤中溶质迁移过程的数值模拟
2015-05-26孙露露杨卫波
孙露露,杨卫波
(扬州大学水利与能源动力工程学院,江苏扬州 225127)
温度梯度作用下非饱和土壤中溶质迁移过程的数值模拟
孙露露,杨卫波*
(扬州大学水利与能源动力工程学院,江苏扬州 225127)
根据非饱和土壤非等温Richard方程、传热与溶质传递方程,建立溶质迁移模型,研究温度梯度作用下入渗速度对土壤温度变化及溶质迁移规律的影响.数值模拟的结果表明:溶质迁移过程中,土壤温度与溶质的物质的量浓度均随时间延续而逐渐升高,随深度的加深而逐渐降低;入渗速度的增加可促进土壤中热量的扩散和对流,增强溶质的对流和弥散作用.
非饱和土壤;温度梯度;渗流;溶质迁移;数值模拟
近年来,溶质在土壤中的迁移机制已成为当前土壤环境控制领域的一个研究热点.非饱和土壤是由固、液、气三相组成的多孔介质,溶质在沿非饱和土壤的水流运动过程中会导致土壤污染.Viotti等[1]建立了一维非饱和土壤中溶质迁移方程,研究了不同输入参数对溶质浓度分布的影响;Kumar等[2]通过无网格Galerkin(element free galerkin,EFG)法分析了二维非饱和多孔介质中溶质迁移问题,并与有限元法进行了算例比较;Javadi等[3]对非饱和土壤中水、气和溶质的迁移进行了案例分析;Ghasemzadeh[4]研究了变形多孔介质中热量、水流和溶质的迁移过程;Winiarski等[5]实验研究了非饱和土壤的非均质性对多相流和溶质迁移特性的影响;眭素刚等[6]开展了非饱和土壤弥散、渗流特性试验,并模拟分析了分层土壤中溶质的浓度分布;左自波等[7]研究了不同降雨条件下非饱和带孔隙水压力、含水量变化及溶质的迁移规律.鉴于溶质类型的多样性,本文以某一特定浓度的无机液体A为代表,在忽略吸附、衰减及化学性质的条件下,根据多孔介质传热、传质及渗流理论,建立非饱和土壤中溶质迁移的数学模型,研究入渗速度对非饱和土壤温度及溶质的物质的量浓度c(A)分布规律的影响,以及渗流作用下非饱和土壤的传热传质规律.
1 计算模型
1.1 物理模型
为模拟渗流影响下土壤温度和溶质浓度的时空变化规律,以非饱和土壤为研究对象,建立溶质迁移模型,进行渗流场、温度场和溶质传递场三场耦合的二维数值模拟,研究温度及溶质的物质的量浓度的分布规律,模拟对象结构如图1所示.图1中ABCD区域为非饱和土壤,模型尺寸为AB=1 m,AD=0.5 m;E(0.5,0.45)为溶质源.溶质迁移在竖直方向上分别取5个观测点,1#(0.5,0.425),2#(0.5,0.4),3#(0.5,0.35),4#(0.5,0.25),5#(0.5,0.1).
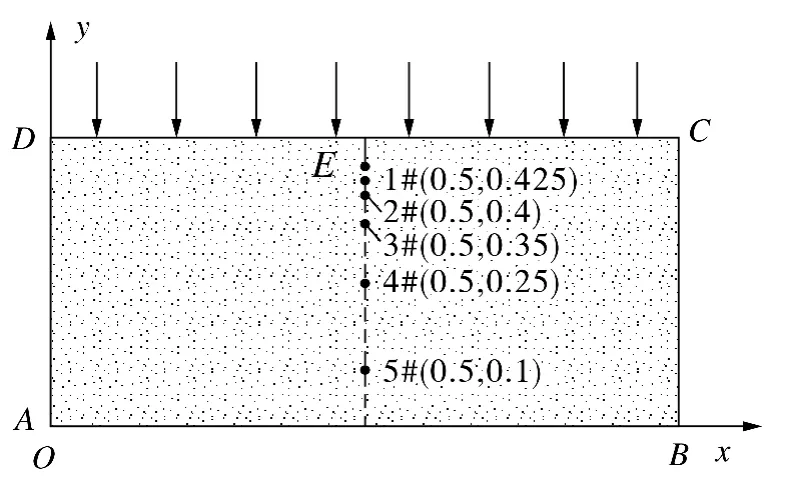
图1 非饱和土壤中溶质迁移模型示意图Fig.1 Schematic diagram of physicalmodelw ith solute transport in unsaturated soils
1.2 数学模型
由于非饱和土壤中渗流、传热及溶质传递是一个多因素互相耦合的复杂过程,为便于模型建立与求解,现作如下简化假设:①土壤水不可压缩;②土壤土质均匀,各向同性;③不存在气体、固体和其他补给及化学反应来源;④水体的密度、导热性和比热容恒定;⑤忽略温度变化对土壤热物理性质的影响.
1)渗流控制方程.非饱和土壤渗流满足Darcy定律[8]:

式中v为渗流速度;k为渗透系数;H为水力水头.
基于质量守恒原理,非饱和土壤二维渗流的非等温Richard方程[9]为
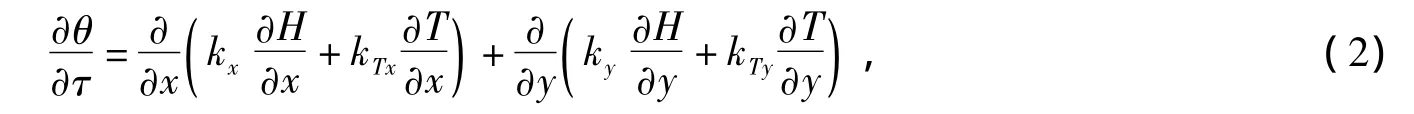
式中θ为土壤体积含水率;τ为时间;kx,ky分别为土壤x与y方向的等温渗透系数;kTx,kTy分别为土壤x与y方向的非等温渗透系数;T为温度.
非饱和土壤中体积含水率和土壤水吸力呈非线性关系,可由土壤物理学领域最为普遍使用的van Genuchten土—水特征曲线通用方程[10]
表示,式中θ为土壤体积含水率;θr为残余体积含水率;θs为饱和体积含水率;ψ为土壤水吸力;n,m,α为模型参数,其中n为土—水特征曲线指数,与曲线的陡缓程度有关且满足n=(1-m)-1.
将van Genuchten土—水特征曲线与土壤渗透系数Mualem模型[11]联合,可得土壤渗透系数的解析表达式:

式中Se=(θ-θr)/(θs-θr)为有效饱和度;kr=k/ks为相对渗透系数,其中ks为饱和渗透系数;m为模型参数.
2)传热控制方程.当土壤中的渗流为稳定流时,热传输方程[8]330为
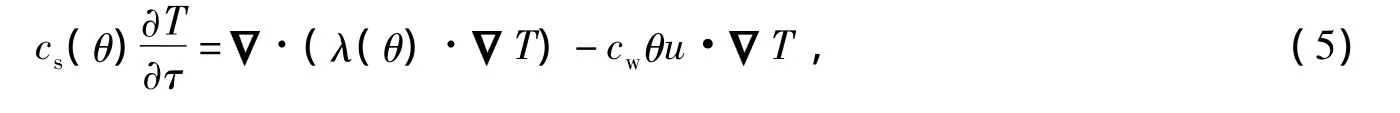
式中cs为土壤比热容;λ为土壤热导率;cw为土壤中流体(水)的比热容;u为渗透速度.
3)溶质传递方程.基于溶质的质量守恒定律,可得非饱和土壤的二维溶质传递方程[8]231:

4)定解条件的确定.
①渗流问题.对于非饱和土壤模型,其顶部CD为速度入口边界条件;AB为常水头边界条件,水头为0;其余边界为无流动边界.非饱和土壤ABCD区域,水头压力初始值为负数.
②传热问题.非饱和土壤模型的AB和CD为温度边界条件,分别为300 K和308 K,其余边界为周期性热条件边界.非饱和土壤ABCD区域初始温度为边界条件下稳定的温度场,如图2所示.
③溶质传递问题.非饱和土壤模型中点E为溶质源,通量边界条件为 0.5 mol·(m2·s)-1,其余为无通量边界条件.整个土壤模型区域水中溶质的初始浓度为0.

图2 非饱和土壤溶质迁移前稳态温度场(K)Fig.2 Tem perature distribution before solute transport in unsaturated soils
1.3 计算参数及数值计算
采用Comsol Multiphysics多物理场耦合分析软件中多孔介质地下水流模块、传热模块及物质传递模块,进行3个物理场的耦合模拟计算.非饱和土壤渗流计算参数由土壤水特性软件Spaw得到:渗透系数k为3.5 ×10-6m·s-1,饱和含水率 θs为0.43,残余含水率 θr为 0.08,土壤密度 ρs为 1 400 kg·m-3,关系常数α,n分别为1.74和1.38;传热计算参数:土壤热导率 λs为 2 W·(m·K)-1,土壤比热容 cs为 2 000 J·(kg·K)-1,水的密度 ρw为1 000 kg·m-3,水的热导率 λw为0.54W·(m·K)-1,水的比热容 cw为4 200 J·(kg·K)-1;溶质传递计算参数:分子扩散系数D为8.25×10-7m2·s-1,水平弥散度αr为0.001 m,垂直弥散度αz为0.002 m.
本文采用三角形网格对非饱和土壤进行自由网格划分,近溶质源区域网格较密,并进行了网格精度检验.由于基本假设中忽略了温度变化对土壤热物理性质的影响,且水体的物性参数恒定,所以实际大气温度波动对溶质迁移的影响较小,可忽略不计.恒定的环境温度条件下,土壤具有稳定且呈线性分布的温度场,形成渗流条件下溶质迁移模型的初始温度梯度,见图2.
2 计算结果及分析
2.1 不同深度处土壤温度及溶质的物质的量浓度分布
对入渗速度为2×10-6m·s-1时非饱和土壤中溶质迁移模型进行数值计算,分别得到第25 h时刻非饱和土壤温度及溶质的物质的量浓度分布云图、不同深度处非饱和土壤温度及溶质的物质的量浓度变化曲线,见图3~6.

图3 第25 h时刻土壤温度(K)分布云图Fig.3 Tem perature distribution cloud graph at 25 h

图4 第25 h时刻溶质的物质的量浓度分布云图Fig.4 Concentration distribution cloud graph at 25 h
由图3可观察得到,土壤温度由上至下逐步降低,与土壤初始时的温度相比有了较大的提升.这主要是由于入渗雨水温度高于土壤本身的初始温度,随着雨水渗流进入土壤,与土壤固体骨架及水分进行导热和对流换热,从而导致温度逐渐升高.由图4可以观察得到,靠近溶质源区域溶质的c(A)越高,远离溶质源区域c(A)越低,且溶质沿竖直方向的迁移较水平方向更大.这是由于溶质在土壤中的迁移与溶质弥散度、水流在土壤中的渗透速度相关,且竖直方向的溶质弥散度及水流的渗透速度均大于水平方向.
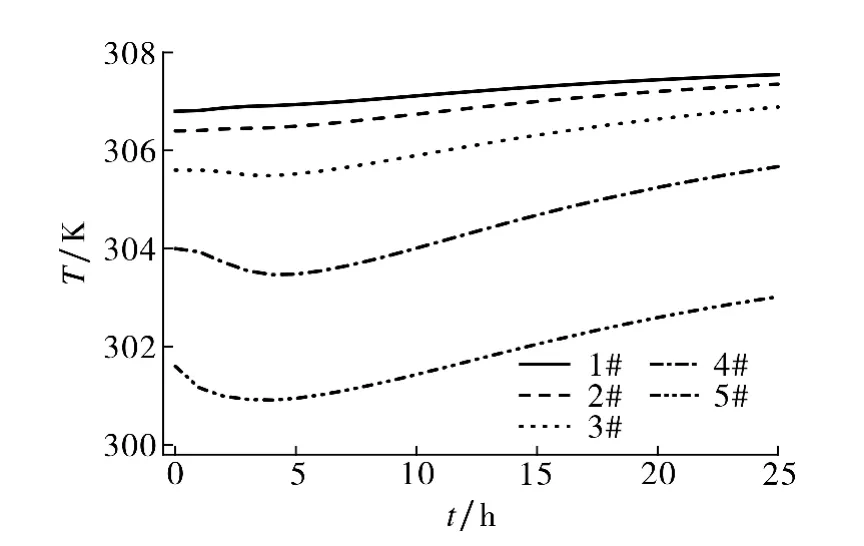
图5 不同深度处土壤温度变化曲线Fig.5 Variations of soil tem perature at different depths
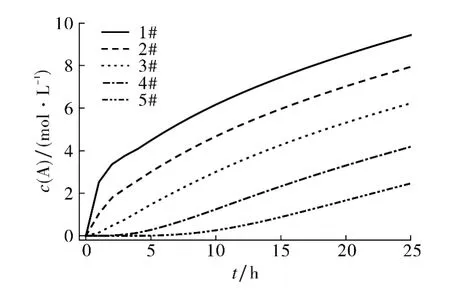
图6 不同深度处溶质的物质的量浓度变化曲线Fig.6 Variations of concentration at different depths
由图5可观察得到,1#处土壤温度最高,5#处最低,且整体随着时间增加而升高.在0~5 h期间,土壤温度有一定波动,越深处波动越明显.这是由于渗流前期土壤逐渐饱和,下层土壤含水率增大导致土壤热导率减小,这与上层土壤热导率差异较大;渗流后期土壤基本饱和,竖直方向热导率差异逐渐缩小.由图6可观察得到,溶质的c(A)随时间变化而不断增大,越接近溶质源区域溶质的c(A)越高且增幅更明显.这是由于越接近土壤地表,溶质的c(A)变化受渗流影响越显著,且随着深度增加影响越小.
2.2 不同入渗速度时土壤温度及溶质的物质的量浓度分布
为分析入渗速度对非饱和土壤温度及溶质的物质的量浓度分布特性的影响,对入渗速度分别为1×10-6,2×10-6,3×10-6m·s-1时溶质迁移模型进行数值计算,分别得到不同入渗速度时非饱和土壤中1#处的温度及溶质的物质的量浓度变化曲线,见图7~8.
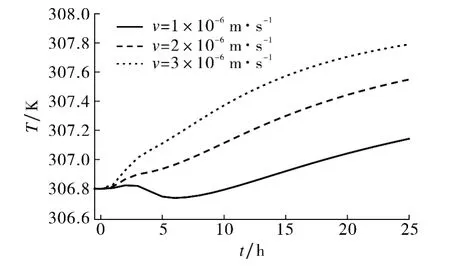
图7 不同入渗速度时1#处土壤温度变化曲线Fig.7 Variations of soil tem perature at 1#for different infiltration rates
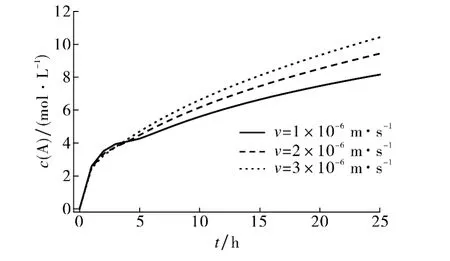
图8 不同入渗速度时1#处溶质的物质的量浓度变化曲线Fig.8 Variations of concentration at 1#for different infiltration rates
由图7观察得到,土壤温度随时间变化大致逐渐升高,且入渗速度越大土壤温升越快;当v=1×10-6m·s-1时,土壤温度波动明显.这是因为渗流初期,入渗速度越小土壤的饱和时间越长,导致上、下层土壤之间的热导率差异缩减缓慢,从而使得土壤温度产生波动.由图8可观察得到,对于同一个观测点1#,在土壤渗流初期,渗流速度越小1#处溶质的c(A)越大;渗流后期,入渗速度越大溶质的c(A)越大.这主要是由于渗流初期土壤非饱和,溶质的对流作用大于弥散作用,当入渗速度加快时溶质对流作用越明显,所以溶质迁移越快,溶质的c(A)增加缓慢;而渗流后期土壤达到饱和,此时弥散作用起主导作用,入渗速度越大水动力弥散系数越大,溶质的c(A)增加越快.综合图7,8可以得到,入渗速度的增加可以促进土壤中热量的扩散和对流,增强溶质的对流作用和弥散作用.
3 结论
1)渗流初期,上、下层土壤含水率不同导致土壤热导率不均匀,对土壤温度变化具有一定影响.
2)越接近土壤地表,溶质的物质的量浓度变化受渗流影响越显著,且随着深度增加,影响越来越小.
3)入渗速度的增加可以促进土壤中热量的扩散和对流,增强溶质的对流作用和弥散作用.
[1] VIOTTIP,PAPINIM P,STRACQUALURSIN,et al.Contaminant transport in an unsaturated soil:laboratory tests and numerical simulationmodel as procedure for parameters evaluation [J].Ecol Model,2005,182(2):131-148.
[2] KUMAR R P,DODAGOUDAR G R.Meshfree analysis of two-dimensional contaminant transport through unsaturated porousmedia using EFGM[J].Int JNumer Meth Biomed Engng,2010,26(12):1797-1816.
[3] JAVADIA A,AL-NAJJAR M M,EVANSB.Numericalmodeling of contaminant transport through soils:case study[J].JGeotech Geoenviron Eng,2008,134(2):214-230.
[4] GHASEMZADEH H.Heat and contaminant transport in unsaturated soil[J].Int JCiv Eng,2008,6(2):90-107.
[5] WINIARSKIT,LASSABATERE L,ANGULO-JARAMILLO R,et al.Characterization of the heterogeneous flow and pollutant transfer in the unsaturated zone in the fluvio-glacial deposit[J].Procedia Environ Sci,2013,19:955-964.
[6] 眭素刚,徐世光,刘文连,等.某渣场污染物在非饱和岩土介质中的迁移模拟研究[J].中南大学学报(自然科学版),2013,44(5):2173-2180.
[7] 左自波,张璐璐,王建华.降雨条件下非饱和土中污染物迁移的数值模拟[J].地下空间与工程学报,2011,7(S1):1347-1352.
[8]仵彦卿.多孔介质渗流与污染物迁移数学模型[M].北京:科学出版社,2011:188-339.
[9]王华军,路俊超,杨宾,等.温度梯度下土壤盐分迁移过程的数值模拟[J].太阳能学报,2014,35(6):1086-1091.
[10] van GENUCHTEN M T.A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Sci Soc Am J,1980,44(5):892-898.
[11] MUALEM Y.A new model for predicting the hydraulic conductivity of unsaturated porousmedia[J].Water Resour Res,1976,12(3):513-522.
Numerical simulation of solute transport in unsaturated soils under tem perature gradient
SUN Lulu,YANGWeibo*
(Sch of Hydr,Energy & Power Engin,Yangzhou Univ,Yangzhou 225127,China)
A model for solute transport in unsaturated soils is established based on the coupled governing equations of non-isothermal flow,heat transfer and solute transport.Numerical analyses are performed to investigate the effects of infiltration rates on the soil temperature variations and solute transport rules under temperature gradient.The results prove that soil temperature and solute concentration of different depths are mainly increasing over time,and both gradually reduce along the depth direction.And furthermore,the increase of the infiltration rate could promote the convection diffusion of heat in the soil and strengthen the advection and dispersion effect of solute.
unsaturated soils;temperature gradient;seepage;solute transport;numerical simulation
TK 124
A
1007-824X(2015)03-0046-05
2015-03-27.* 联系人,E-mail:yangwb2004@163.com.
中国科学院可再生能源重点实验室资助项目(y507k51001);江苏省自然科学基金资助项目(BK20141278);热流科学与工程教育部重点实验室(西安交通大学)开放基金资助项目(KLTFSE2014KF05);广西建筑新能源与节能重点实验室开放基金资助项目(桂林能15-J-22-3).
孙露露,杨卫波.温度梯度作用下非饱和土壤中溶质迁移过程的数值模拟[J].扬州大学学报(自然科学版),2015,18(3):46-50.
(责任编辑 贾慧鸣,青 禾)
