一类受食物资源影响的禽流感模型的渐近性态

葛 静，陈晓东，张群英

（1.扬州大学数学科学学院，江苏 扬州 225002；2.淮阴师范学院数学科学学院，江苏 淮安 223300；3.江苏联合职业技术学院，江苏 淮安 223200）

一类受食物资源影响的禽流感模型的渐近性态

葛 静1，2，陈晓东3，张群英1＊

（1.扬州大学数学科学学院，江苏 扬州 225002；2.淮阴师范学院数学科学学院，江苏 淮安 223300；3.江苏联合职业技术学院，江苏 淮安 223200）

研究一类新的禽流感模型，考察了禽类食物资源对禽流感传播过程的影响.分别给出禽类系统和全系统的基本再生数，并且分析了两种系统的动力学性质.理论结果和数值模拟表明，禽类丰富的食物资源增加了人类和禽类感染禽流感的风险.

传染病模型；禽流感；食物资源；稳定性

自1997年发现禽流感病毒在人群中传播以来，高致病的禽流感病毒严重威胁着人类的生命和财产安全.数学上对传染病的研究主要通过建立反映传染病动力学特性的模型，并对模型动力学性态进行定性、定量分析和数值模拟，以揭示其发展规律，预测其变化趋势，寻求对其预防和控制的最优策略.最早用于研究传染病的数学模型是著名的SIR仓室模型［1］.近年来，人们应用大量的数学模型分析各种类型的传染病，如Xu［2］，朱佳怡［3］和李天擎［4］等分别考虑了潜伏期、温度、政府干预等因素对传染病传播过程的影响，Lei等［5］研究了具自由边界的传染病模型.最近，Iwami等［6］提出利用一种禽类－人类的禽流感传染病模型来解释变异禽流感的传播，Kim［7－8］和Tang［9］等又将该涉及变异禽流感的模型推广到带时滞项的反应扩散系统.上述这些禽流感模型均没有考虑食物资源对禽类的影响，常常假设禽类总数是常数或者满足简单的Logistic方程.通常禽流感传播的周期很短，因此不妨假设一个地区人类的出生率和死亡率相等，即人口总数是常数.事实上，由于受地区禽类食物资源的影响，禽流感的传播在不同地区不尽相同，本文将修改文献［6］3中禽类的增长方程，从而推广经典的SIR仓室模型.

1 模型的建立

本文主要研究如下禽流感系统：

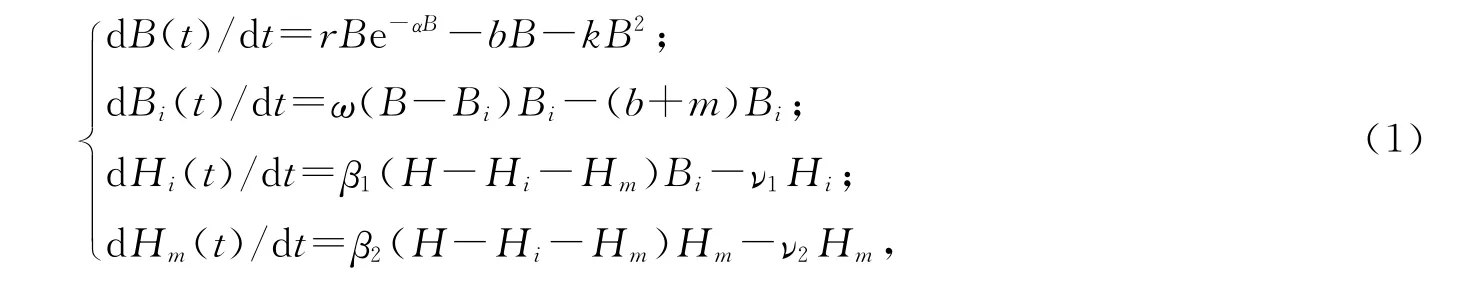
其中B（t）表示t时刻一个地区的禽类总数；Bi（t）表示t时刻感染禽流感病毒的禽类数量；b表示禽类的自然死亡率；r表示禽类的出生率，且r＞b；k表示禽类内部对食物的竞争率；H表示一个地区的人口总数；H i（t）表示t时刻感染禽流感病毒的人数；H m（t）表示t时刻感染变异禽流感病毒的人数；ν1表示感染禽流感病毒之人的恢复率；ν2表示感染变异禽流感病毒之人的恢复率；β1表示未感染禽流感之人接触感染禽流感禽类的概率；β2表示未感染禽流感之人接触感染变异禽流感患者的概率；ω表示未感染的禽类接触感染禽流感禽类的概率；m表示禽类的因病死亡率；α表示一个地区禽类食物资源的分布情况，α越小表明该地区禽类的食物资源越丰富；以上这些变量和参量均取正值.

2 稳定性分析

由于系统（1）中第一、第二个方程仅与禽类有关且是独立的，故考虑它们组成的禽类系统

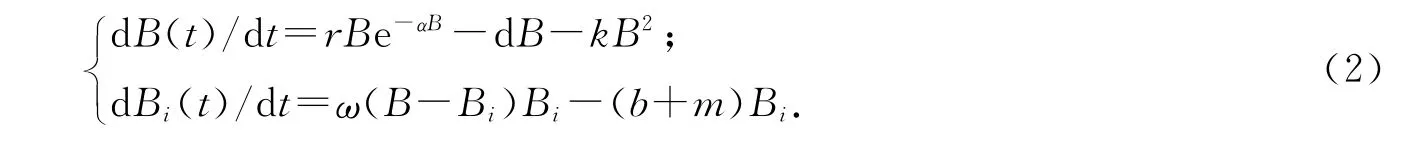
定理1 系统（2）在e01＝（0，0）处总是不稳定的，且

（i）当r0＜1时，在e02＝（B＊，0）处局部渐近稳定；

（ii）当r0＞1时，在e02＝（B＊，0）处不稳定，此时在正平衡点e＋＝（B＊，）处局部渐近稳定.

证明 在e01，e02，e＋处分别对系统（2）进行线性化，得到相应的特征方程.对于e01而言，其对应的特征方程为［λ－（r－b）］（λ＋b＋m）＝0.显然它有一个正根r－b，所以系统（2）在e01处总是不稳定的.对于e02而言，其相应的特征方程为（λ＋rαB＊e－αB＊＋k B＊）［λ－ωB＊＋（b＋m）］＝0.当r0＜1时，该特征方程的两个根均为负，故在e02＝（B＊，0）处是局部渐近稳定的；当r0＞1时，该特征方程有一个正根λ＝ωB＊－（b＋m），故系统（2）在e02＝（B＊，0）处是不稳定的.对于正平衡点e＋＝（B＊，），其对应的特征方程为（λ＋rαB＊e－αB＊＋k B＊）（λ＋）＝0.该方程的两根显然为负，故当r0＞1时，系统（2）在正平衡点e＋＝（B＊，）处是局部渐近稳定的.

接下来讨论全系统（1）的平衡点及其稳定性.

易知全系统（1）有平凡平衡点P01＝（0，0，0，0）；无病平衡点P02＝（B＊，0，0，0）；感染禽流感平衡点P03＝（B＊，Bi＊，β1／（ν1＋β1），0）；当β2H＞ν2时，存在感染变异禽流感平衡点P04＝（0，0，0，H－ν2／β2），P05＝（B＊，0，0，H－ν2／β2）；而当r0＞1时，若取，则R0＞1时，存在唯一的正平衡点P＊＝（），即感染禽流感和变异禽流感的平衡点，其中B＊，如前所述，

定理2 系统（1）在P01，P04处总是不稳定的，

（i）当r0＜1且β2H＜ν2时，在P02处是局部渐近稳定的；

（ii）当r0＞1且R0＜1时，在P03处局部渐近稳定；

（iii）当r0＞1且R0＞1时，在P＊处局部渐近稳定；

（iv）当r0＜1且β2H＞ν2时，在P05处是局部渐近稳定的.

证明 由定理1的证明知，系统（1）在P01，P04处总是不稳定的.

（i）对系统（1）线性化，得P02＝（B＊，0，0，0）处的特征方程为

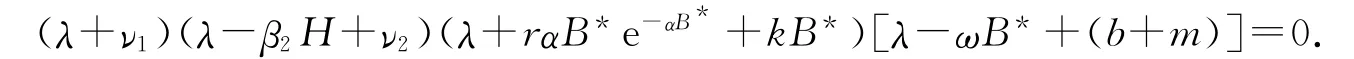
当r0＜1且β2H＜ν2时，该方程的根均为负值，故系统（1）在P02处是局部渐近稳定的.

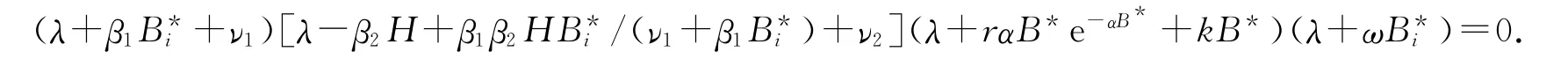
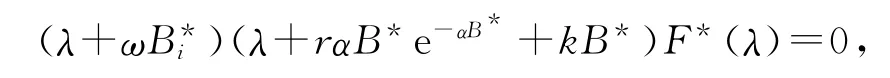
（iv）系统（1）在P05＝（B＊，0，0，H－ν2／β2）处的特征方程为

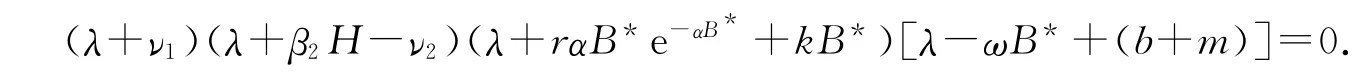
易知当r0＜1且β2H＞ν2时，该方程的根均为负值，这说明系统（1）在P05处是局部渐近稳定的.

注1 注意到r0关于α单调递减，而R0关于α单调递增，这表明一个地区丰富的食物资源易导致禽类禽流感的发生，且人类较易感染普通禽流感病毒，但此时人类感染变异禽流感病毒的概率反而会降低.

3 数值模拟

利用 Matlab软件对系统（1）进行数值模拟，选取合适的数据如下［10－11］：

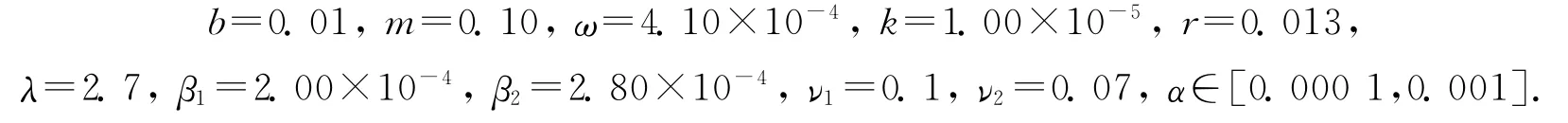
不妨假设初始时刻禽类总数B为500个.为考察食物资源对禽流感传播的影响，首先选择α＝0.001，此时r0＝0.747＜1，β2H＝0.14＞ν2＝0.07，可绘出系统（1）的模拟曲线，见图1.由图1可观察到，当t→＋∞时，H i→0，Bi→0，即感染禽流感的人或禽类逐渐消失，这与定理2（iv）的理论结果一致；其次，选择α＝0.000 1，此时r0＝1.007＞1，R0＝1.371＞1，可绘出系统（1）的模拟曲线，见图2.由图2可观察到，当t→＋∞时，感染禽流感和变异禽流感的人或禽类总是存在的，这与定理2（iii）的理论结果一致.

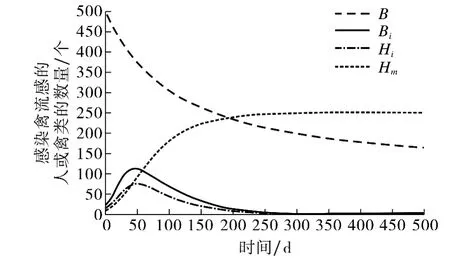
图1 当α＝0.001时，感染禽流感的人或禽类逐渐消失Fig.1 Whenα＝0.001，human and bird infected with avian influenza disappear gradually

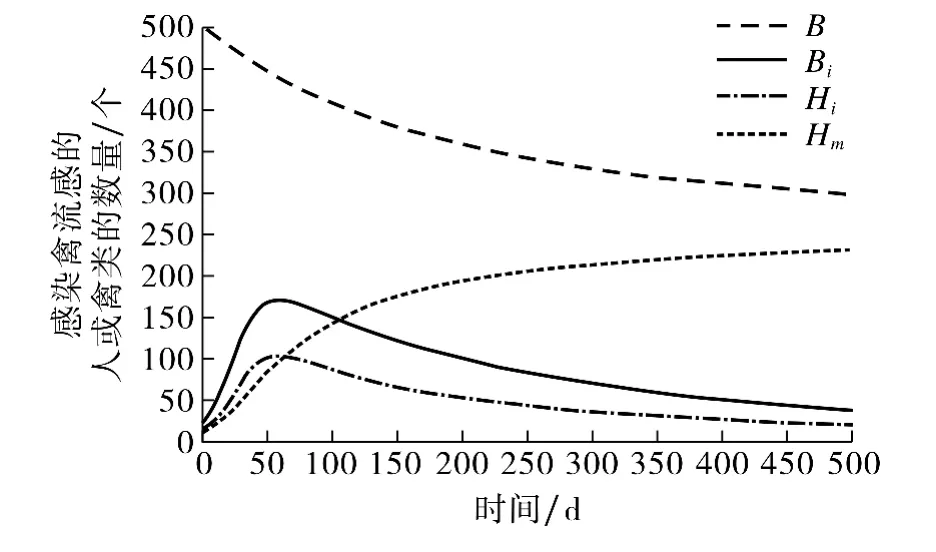
图2 当α＝0.000 1时，感染禽流感的人或禽类总存在Fig.2 Whenα＝0.000 1，human and bird infected with avian influenza always exist

［1］马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究 ［M］.北京：科学出版社，2006：4－10.

［2］XU Rui.Global dynamics of an SEIS epidemic model with saturation incidence and latent period［J］.Appl Math Comput，2012，218（15）：7927－7938.

［3］朱佳怡，朱晓萍，林支桂.2013年H7N9型禽流感疫情的数学分析 ［J］.扬州大学学报（自然科学版），2014，17（3）：6－8，18.

［4］李天擎，张磊，刘燕红，等.政府干预对H7N9禽流感疫情的影响 ［J］.扬州大学学报（自然科学版），2015，18（2）：22－25.

［5］LEI Chengxia，KIM K I，LIN Zhigui.The spreading frontiers of avian－human influenza described by the free boundary［J］.Sci China Math，2014，57（5）：971－990.

［6］IWAMI S，TAKEUCHI Y，LIU Xianning.Avian－human influenza epidemic model［J］.Math Biosci，2007，207（1）：1－25.

［7］KIM K I，LIN Zhigui.Asymptotic behavior of an SEI epidemic model with diffusion［J］.Math Comput Modelling，2008，47（11／12）：1314－1322.

［8］KIM K I，LIN Zhigui，ZHANG Lai.Avian－human influenza epidemic model with diffusion［J］.Nonlinear Anal：Real Word Appl，2010，11（1）：313－322.

［9］TANG Qiulin，GE Jing，LIN Zhigui.An SEI－SI avian－human influenza model with diffusion and nonlocal delay［J］.Appl Math Comput，2014，247：753－761.

［10］JUNG E，IWAMI S，TAKEUCHI Y，et al.Optimal control strategy for prevention of avian influenza pandemic［J］.J Theoret Biol，2009，260（2）：220－229.

［11］WAN Hui，ZHU Huaiping.The impact of resource and temperature on malaria transmission［J］.J Biol Syst，2012，20（3）：285－302.

The asymptotic behavior of an avian－human influenza model with the impact of food resource

GE Jing1，2，CHEN Xiaodong3，ZHANG Qunying1＊

（1.Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China；2.Sch of Math Sci，Huaiyin Norm Univ，Huai’an 223300，China；3.Jiangsu Union Tech Inst，Huai’an 223200，China）

This paper deals with a new model describing the avian－human influenza.The impact of food resources for birds on the transmission of disease is considered.The basic reproduce numbers for the bird system and full system are provided and a dynamical analysis for the system is given.Theoretical results and numerical simulations show that the abundance of food resources for birds increases the risk for the bird and human to be infected by the avian influenza.

epidemic model；avian－human influenza；food resource；stability

O 175.26

A

1007－824X（2015）03－0012－04

2015－05－04.＊ 联系人，E－mail：qyzhang＠yzu.edu.cn.

国家自然科学基金资助项目（11501494）；江苏省2012年“青蓝工程”资助项目；江苏省2015年高校研究生科研创新计划资助项目（KYLX15－1353）.

葛静，陈晓东，张群英.一类受食物资源影响的禽流感模型的渐近性态 ［J］.扬州大学学报（自然科学版），2015，18（3）：12－15.

（责任编辑 青 禾）