一类具反馈控制传染病模型的稳定性分析

朱 莹，凌 智

（1.扬州大学数学科学学院，江苏 扬州 225002；2.扬州职业大学数学科学学院，江苏 扬州 225009）

一类具反馈控制传染病模型的稳定性分析

朱 莹1，2，凌 智1＊

（1.扬州大学数学科学学院，江苏 扬州 225002；2.扬州职业大学数学科学学院，江苏 扬州 225009）

研究一类具反馈控制和标准发生率的SI传染病模型，运用常微分方程平衡点的理论，证明了该系统无病平衡点的全局渐近稳定性和局部渐近稳定性.通过构造适当的Lyapunov函数，证明了该系统染病平衡点的局部渐近稳定性，给出疾病趋于消失或地方性流行的一个充分条件.最后通过数值模拟验证了所得结论的正确性.

反馈控制；传染病模型；标准发生率；局部稳定性；全局稳定性

传染病对人类健康带来了极大威胁，比如20世纪80年代开始蔓延的艾滋病毒；2003年突袭人类的SARS；2013年3月底在中国内地率先发现的H7N9型禽流感病毒等.这些传染性疾病不仅会给人们带来极大的恐慌，而且还会导致数以万计的人类个体失去生命，于是有关数学模型［1－4］的建立成为分析疾病传播与控制疾病的基本工具.许多学者运用传染病动力学中古典的仓室模型对传染病进行了描述与研究［5－8］，常见的传染病模型有SI模型、SIS模型、SEI模型和SIR模型等.由于现实生态系统中生存率等一些生物参数是变化的，因此人们更加关心生态系统能否经受持续一段时间且不可预测的干扰.Gopalsamy等［9］在Logistic模型中引入一个反馈控制变量，并讨论了这个具反馈控制模型解的渐近行为.这种具反馈控制变量的传染病模型受到了广泛关注［10－11］，研究表明：若模型正平衡解全局渐近稳定，则反馈控制变量不会改变模型的稳定性而只会改变模型正平衡解的位置；若模型中传染病灭绝，则反馈控制变量可使模型变得全局渐近稳定或传染病持续灭绝.鉴于反馈控制变量对传染病模型的动力学行为有着重要的影响，故本文研究如下一类具标准发生率和反馈控制的SI传染病模型：

其中S（t）和I（t）分别表示易感者和感染者在t时刻的密度；u1（t）和u2（t）为反馈控制变量；r为易感人群的补充率；μ为染病者的死亡率；b为易感人群接触染病者时的转化率；a，f分别为易感人群与染病人群内部竞争系数；c1，c2，d1，d2，e1，e2为参量；以上变量和参量均取正值.在数学生态学中，只须考虑模型（1）的正解，因此假定模型（1）的初始条件S（0），u1（0），I（0），u2（0）均为正值，从而易得当t＞0时，具初始条件的模型（1）所有解都是正值.

1 无病平衡点的局部稳定性与全局稳定性

假定模型（1）的无病平衡点为P0（S0，0，，0），其中；染病平衡点为），当且仅当下述方程有正解：

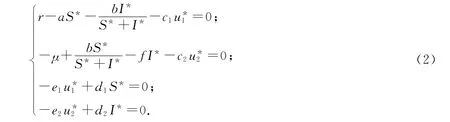
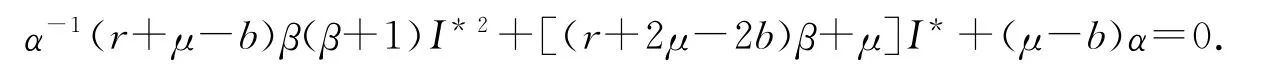
由解的正性，知当μ＜b＜r＋μ时，可得

再由μ＜b＜r＋μ，可知（μ－b）（r＋μ－b）＜0，此时易知模型（1）的基本再生数为

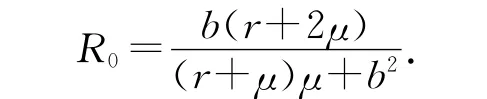
下面分别讨论模型（1）无病平衡点P0的稳定性及染病平衡点P＊的稳定性.

定理1 当R0＜1时，模型（1）的无病平衡点P0是局部渐近稳定的；当R0＞1时，P0是不稳定的.

证明 考虑模型（1）在点P0（S0，0，，0）处的Jacobian矩阵

其对应的特征多项式为

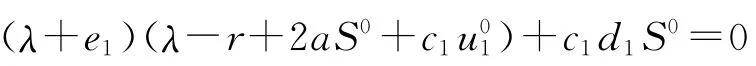
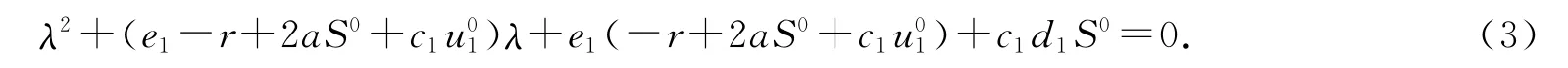
将S0，代入式（3），易得，从而可知另两根的实部小于0.由上述特征方程的4个特征根实部皆为负值，根据Routh－Hurwitz定理可知无病平衡点P0是局部渐近稳定的.

定理2 当R0＜1时，模型（1）的无病平衡点P0是全局渐近稳定的；当R0＞1时，P0是不稳定的.

证明 当R0＜1时，易知模型（1）满足μ＞b＞0，S＞0，I＞0，且1＞S／（S＋I）.由模型（1）中第二式得到I′（t）≤－（μ－b）I，于是I（t）≤I（0）e－（μ－b）t.当t→∞时，有I（t）→0，进而有u2（t）→0，S（t）→S0，u1（t）→u01.这说明当R0＜1时，无病平衡点P0是全局渐近稳定的；当R0＞1时，P0是不稳定的.

2 染病平衡点的局部稳定性

定理3 当R0＞1且4aα（β＋1）＞b时，模型（1）的染病平衡点P＊是局部稳定的.证明 根据常微分方程稳定性原理构造如下Lyapunov函数：

对V（t）求导数，并将方程（2）代入V′（t），得

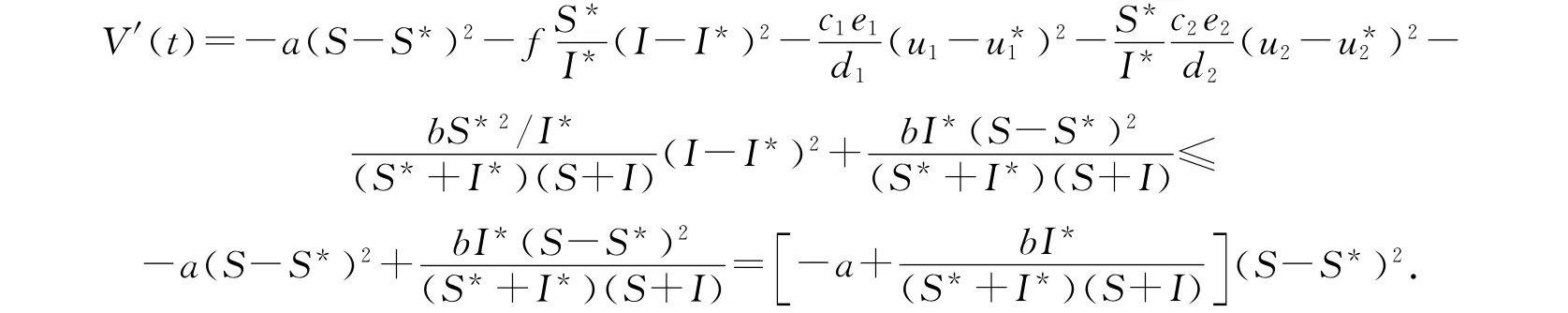
当S→S＊，I→I＊，u1→，u2→时，有

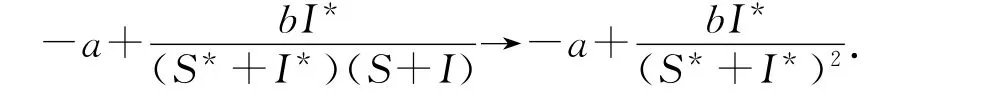
因S＊＝α＋βI＊，故有

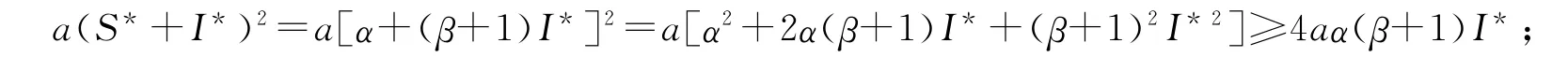
从而，当4aα（β＋1）＞b时，有a（S＊＋I＊）2≥4aα（β＋1）I＊＞bI＊，即

所以V′（t）≤0.即模型（1）的染病平衡点P＊（S＊，I＊，u1＊，u2＊）是局部渐近稳定的.

3 数值模拟

现利用Matlab软件对模型（1）进行数值模拟（见图1～2），以阐明上述3个定理的现实意义.

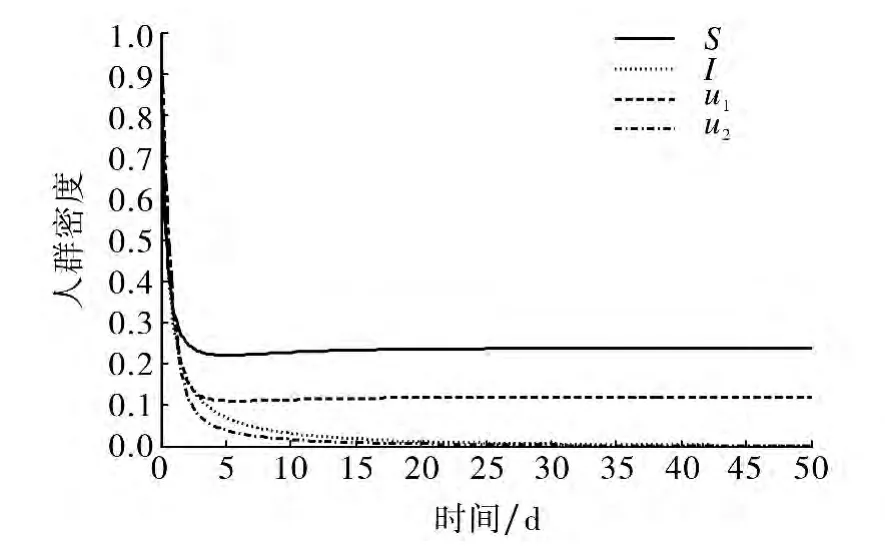
图1 当b＝0.2时传染病消失曲线Fig.1 When b＝0.2 the disease is extinct

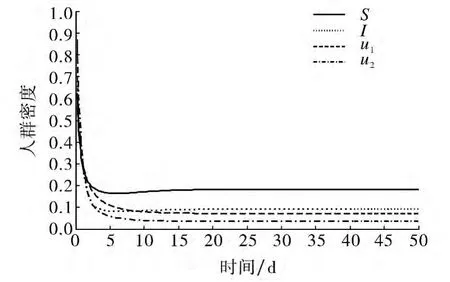
图2 当b＝0.5时传染病流行曲线Fig.2 When b＝0.5 the disease is endemic

对模型（1）的参数进行赋值，选取适当的数据［11］55如下：

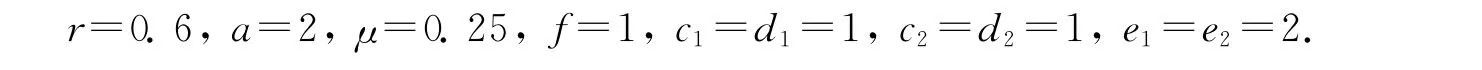
考察参数b，当b＝0.2时，得R0＝0.87＜1，此时无病平衡点为P0（0.24，0，0.12，0），见图1；当b＝0.5时，得R0＝1.19＞1.此时染病平衡点P＊（0.183 4，0.072 4，0.091 7，0.036 2），见图2.

由图1可观察到，此时S和u1趋于正常数S0和u01，I和u2趋近于0，说明疾病趋于消失，这与前述定理1、定理2的结论一致；由图2可观察到，此时S，I，u1，u2分别趋于正常数S＊，I＊，u＊1，u＊2，疾病趋于流行，这与定理3的结论一致.

［1］ANITA L I，ANITA S.Internal eradicability of a diffusive epidemic system via feedback control［J］.Nonlinear Anal：Real World Appl，2011，12（4）：2294－2303.

［2］ANITA S，CAPASSO V.Stabilization of a reaction－diffusion system modelling a class of spatially structured epidemic systems via feedback control［J］.Nonlinear Anal：Real World Appl，2012，13（2）：725－735.

［3］朱佳怡，朱晓萍，林支桂.2013年H7N9型禽流感疫情的数学分析 ［J］.扬州大学学报（自然科学版），2014，17（3）：6－8，18.

［4］李天擎，张磊，刘燕红，等.政府干预对H7N9型禽流感疫情发展的影响 ［J］.扬州大学学报（自然科学版），2015，18（2）：22－25.

［5］朱林涛.一类具扩散SEI传染病模型及其自由边界问题 ［D］.扬州：扬州大学，2012.

［6］王静.两类传染病模型的定性分析 ［D］.上海：华东师范大学，2012.

［7］KIM K I，LIN Zhigui.Asymptotic behavior of an SEI epidemic model with diffussion［J］.Math Comput Model，2008，47（11／12）：1314－1322.

［8］林支桂.数学生态学导引 ［M］.北京：科学出版社，2013：202－216.

［9］GOPALSAMY K，WEN Peixuan.Feedback regulation of Logistic growth［J］.Int J Math Sci，1993，16（1）：177－192.

［10］ZHANG Jiancheng，SUN Jitao.Stability analysis of an SIS epidemic model with feedback mechanism on networks［J］.Phys A，2014，394：24－32.

［11］CHEN Lijuan，SUN Jitao.Global stability of an SI epidemic model with feedback controls［J］.Appl Math Lett，2014，28：53－55.

The stability analysis of an epidemic model with feedback controls

ZHU Ying1，2，LING Zhi1＊

（1.Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China；2.Sch of Math Sci，Yangzhou Polytech Coll，Yangzhou 225009，China）

This paper studies an epidemic model with model feedback controls and standard incidence.Using the balance theory of ordinary differential equations，it proves that the system is global asymptotic stability of the disease－free equilibrium and the locally asymptotic stability.By constructing suitable Lyapunov function，it also proves that the system have the locally asymptotic stability of the equilibrium.A sufficient condition is given for the disease to disappear or endemic.Finally，numerical simulation verifies the validity of the main results.

feedback control；epidemic model；standard incidence；locally stability；global stability

O 175.26

A

1007－824X（2015）04－0033－04

2015－05－28.＊ 联系人，E－mail：zhling＠yzu.edu.cn.

国家自然科学基金资助项目（11571301，61472343）；江苏省自然科学基金资助项目（BK20151305）；江苏省高等职业院校国内高级访问学者计划资助项目（2014FX093）.

朱莹，凌智.一类具反馈控制传染病模型的稳定性分析 ［J］.扬州大学学报（自然科学版），2015，18（4）：33－36.

（责任编辑 青 禾）