一类Hopf代数的单Yetter－Drinfeld模

张 颖，陈惠香

（1.淮海工学院理学院，江苏 连云港 222005；2.扬州大学数学科学学院，江苏 扬州 225002）

一类Hopf代数的单Yetter－Drinfeld模

张 颖1，陈惠香2＊

（1.淮海工学院理学院，江苏 连云港 222005；2.扬州大学数学科学学院，江苏 扬州 225002）

研究一类有限维分次Hopf代数H的单Yetter－Drinfeld模.利用H的生成元在单Yetter－DrinfeldH－模上的作用，给出单Yetter－DrinfeldH－模的结构和同构分类.

Hopf代数；Yetter－Drinfeld模；单Yetter－Drinfeld模

Hopf代数H上 Yetter－Drinfeld模（YDH－模）又称为交叉双模，最初由 Yetter［1］引入.YDH－模的理论有着广泛的应用［2－4］.Makhlouf等［5］证明了当H的反极S是双射时，YDH－模范畴（HYDH）是一个辫子monoidal范畴，因此每一个YDH－模提供了Yang－Baxter方程的一个解；当H是有限维Hopf代数时，HYDH与Drinfeld doubleD（H）－模范畴是等价的.2009年，Cibils等［6］利用n阶循环群代数上的一个二维Yetter－Drinfeld模构造了一类新的Hopf代数H，本文拟利用Radford［7］和Zhu等［8］的工作确定H上单Yetter－Drinfeld模的结构和同构分类.

1 预备知识

本文中恒设k是一个特征为p＞0的代数闭域，所有的代数和模都是域k上的向量空间，代数上的模均为左模，n是一个被p整除的正整数.有关代数的表示及其模等基本概念可参考文献［9］.当p＝2时，Cibils等［6］4035构造的Hopf代数H的结构可描述如下：作为k－代数，H由g，a，b生成，关系式为：g n＝1，g－1ag＝a，g－1bg＝a＋b，a2＝0，b4＝0，baba＝abab，b2a＝ab2＋aba.H的余乘法、余单位和反极S分别由下述等式确定：Δg＝g⊗g，Δa＝a⊗1＋g⊗a，Δb＝b⊗1＋g⊗b；ε（g）＝1，ε（a）＝ε（b）＝0；S（g）＝g－1，S（a）＝－g－1a，S（b）＝－g－1b.由文献［6］4035中推论3.4知H是维数为16n的有限维分次pointed Hopf代数，令

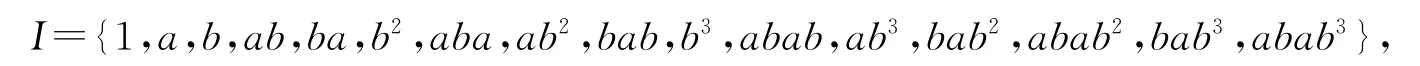
则集合｛g ix｜x∈I，0≤i≤n－1｝是H的一组k－基.设X是一个左H－模，则X⊗H∈HYDH，X⊗H的左H－模作用和右H－余模作用由下式给出：

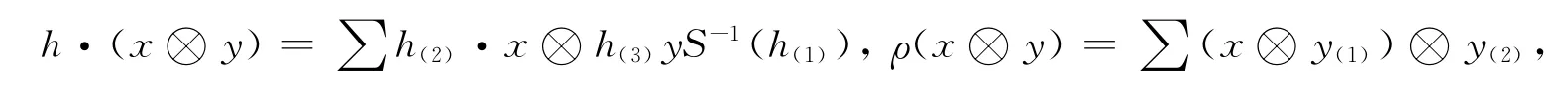
其中h，y∈H，x∈X.Radford［7］678证明了任一单YDH－模M必然满足M≅H·N，其中N是X⊗H的一个单子余模，X是单H－模.若H是一个pointed Hopf代数，则由文献［7］684中引理3知N是一维的，且x⊗y是N的一组k－基，其中x∈X，y∈G（H）；因此，H·N＝H·（x⊗y）.

2 主要结论

群代数kG是H的余根.设n＝2st，其中（2，t）＝1，s≥1，并设ξ∈k是一个t次本原单位根.由文献［10］中定理1知H有t个互不同构的单模Si，0≤i≤t－1，且每个单模Si都是一维的，Si的模结构为g·v＝ξiv，a·v＝b·v＝0，v∈Si.由于H是pointed Hopf代数，故Si⊗H的任一单子余模N是一维的，N中任一非零元素形如v⊗g j（0≤j≤n－1），其中0≠v∈Si.由上述分析知要计算单YDH－模只须考虑YDH－模H·（v⊗g j）即可，记为H（Si，g j），其中0≤i≤t－1，0≤j≤n－1.通过计算得Δ2（g）＝g⊗g⊗g，Δ2（a）＝a⊗1⊗1＋g⊗a⊗1＋g⊗g⊗a，Δ2（b）＝b⊗1⊗1＋g⊗b⊗1＋g⊗g⊗b，S－1（a）＝g－1a，S－1（b）＝bg－1＝g－1a＋g－1b.

引理1 设0≤j≤n－1，则在H（S0，g j）中有下述结论成立：

1）当j是偶数时，g·（v⊗gj）＝v⊗gj，a·（v⊗gj）＝b·（v⊗g j）＝0，此时，dimH（S0，g j）＝1；

2）当j是奇数时，g·（v⊗g j）＝v⊗gj，a·（v⊗g j）＝0，b·（v⊗g j）＝v⊗ag j－1，b2·（v⊗gj）＝v⊗abgj－2＋v⊗bagj－2，b3·（v⊗gj）＝0，此时，dimH（S0，g j）＝3.

证明 由H（S0，g j）上的左H－模作用的定义和文献［11］中命题4.1，直接验证可得上述结论中各等式.显然，集合｛xg i｜x∈I，0≤i≤n－1｝也是H的一组k－基，将基中每个元素作用在v⊗g j上，再由这些等式即知H（S0，g j）的维数.证毕.

命题2 设0≤j≤n－1，则H（S0，gj）是一个单YDH－模.

证明 由引理1知线性空间k（v⊗g j）是H（S0，g j）中唯一的单余子模，从而H（S0，g j）是单YDH－模.

命题3 设1≤i≤t－1，0≤j≤n－1，则H（Si，gj）是一个单YDH－模，dimH（Si，g j）＝16.

证明 由于特征p＝2，故可分以下2种情形计算H在H（Si，g j）上的作用.

1）当j为偶数时，直接验证可得下述等式：

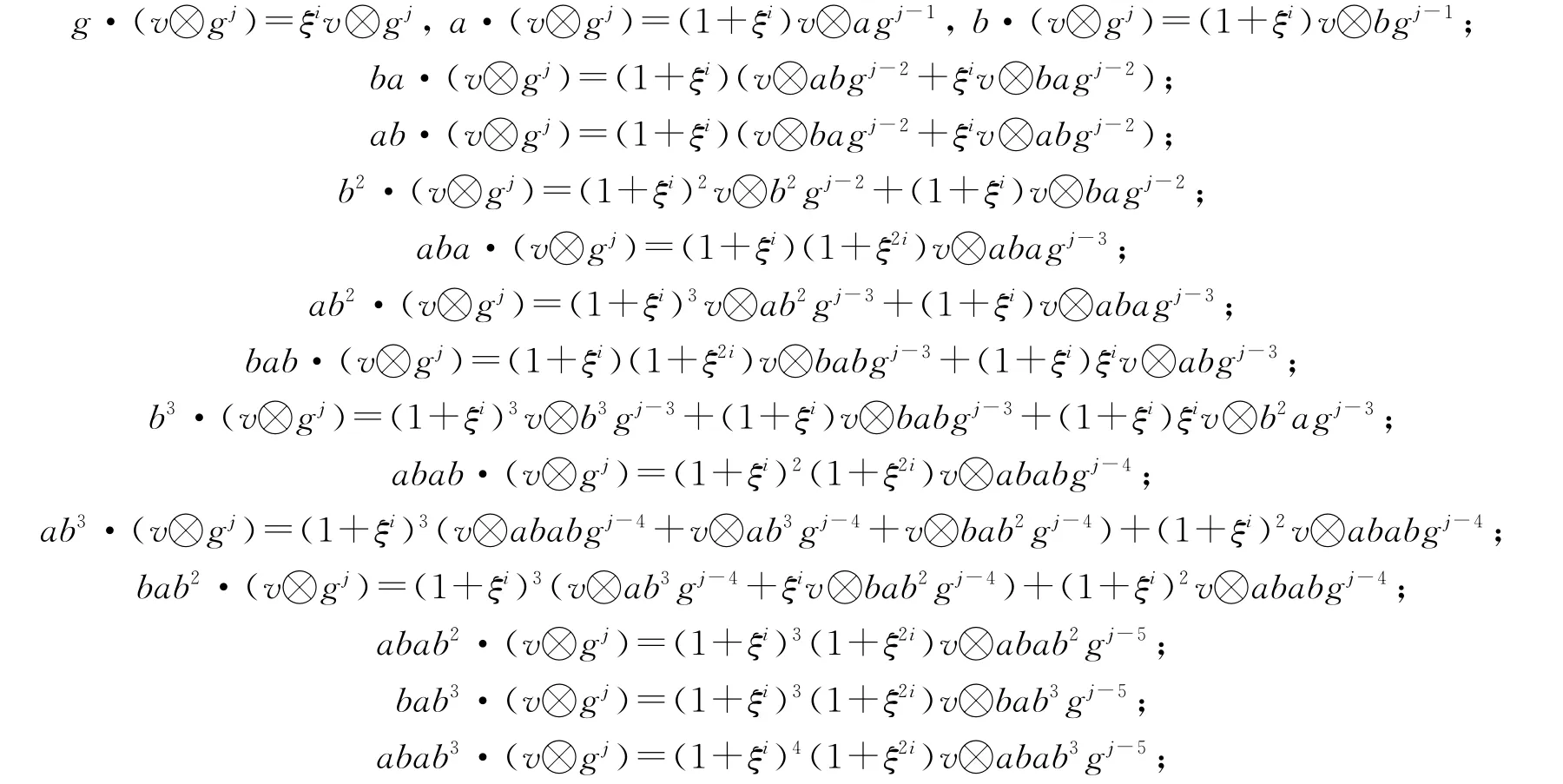
2）当j为奇数时，直接验证可得下述等式：

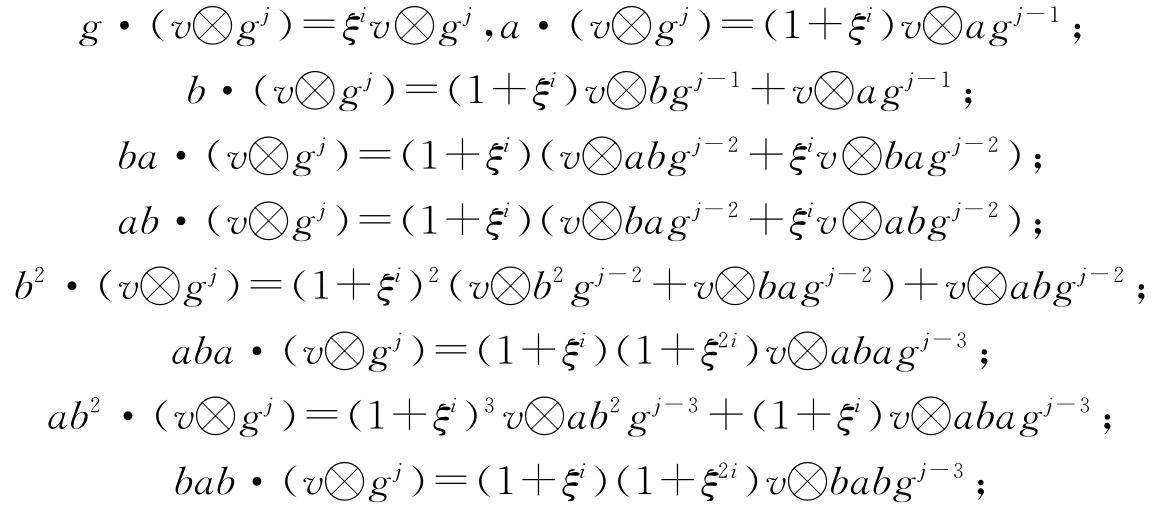
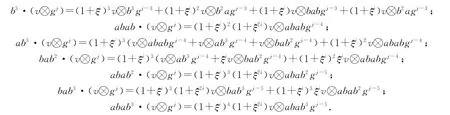
因ξ是一个t次本原单位根且（2，t）＝1，故1＋ξ2i≠0，其中1≤i≤t－1.由集合｛xgi｜x∈I，0≤i≤n－1｝是H的一组k－基，将基中的每个元素作用在v⊗gj上，再由命题3证明1）和2）中全体等式可知集合｛x·（v⊗g j）｜x∈I｝是H（Si，g j）的一组基，且线性空间k（v⊗g j）是H（Si，g j）中唯一的单子余模；因此，H（Si，g j）是单YDH－模，且dimH（Si，g j）＝16.证毕.

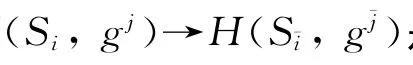
由上述引理及命题，即得单YDH－模的分类定理.

定理5 所有互不同构的单YDH－模分类如下：

1）2s－1t个一维的单YDH－模：H（S0，g j），其中j为偶数，且0≤j≤n－1；

2）2s－1t个三维的单YDH－模：H（S0，g j），其中j为奇数，且0≤j≤n－1；

3）（t－1）n个维数为16的单YDH－模：H（Si，g j），其中1≤i≤t－1，0≤j≤n－1.

［1］YETTER D N.Quantum groups and representations of monoidal categories［J］.Math Proc Cambridge Philos Soc，1990，108（2）：261－290.

［2］SEMIKHATOV A M.Fusion in the entwined category of Yetter－Drinfeld modules of a rank－1 Nichols algebra［J］.Theoret ＆ Math Phys，2012，173（1）：1329－1358.

［3］HECKENBERGER I，SCHNEIDER H J.Yetter－Drinfeld modules over bosonizations of dually paired Hopf algebras［J］.Adv Math，2013，244（13）：354－394.

［4］JOSÉ－NICANOR AÁ，RAMÓN G R，CARLOS S C.Yetter－Drinfeld modules over weak braided Hopf monoids and center categories［J］.Acta Math Sin，2014，30（4）：567－590.

［5］MAKHLOUF A，PANAITE F.Yetter－Drinfeld modules for Hom－bialgebras［J］.J Math Phys，2014，55（1）：01350101－01350117.

［6］CIBILS C，LAUVE A，WITHERSPOON S.Hopf quivers and Nichols algebras in positive characteristic［J］.Proc Amer Math Soc，2009，137（12）：4029－4041.

［7］RADFORD D E.On oriented quantum algebras derived from representations of the quantum double of a finite dimensional Hopf algebra［J］.J Algebra，2003，270（2）：670－695.

［8］ZHU Hong，CHEN Huixiang.Yetter－Drinfeld modules over the Hopf－ore extension of the group algebra of dihedral group［J］.Acta Math Sin，2012，28（3）：487－502.

［9］AUSLANDE M，REITE I，SMALØS O.Representations theory of Artin algebras［M］.Cambridge：Cambridge Univ Press，1997：1－48.

［10］张颖，陈惠香.两个Hopf代数的单模及主不可分解模 ［J］.扬州大学学报（自然科学版），2011，14（2）：10－12.

［11］ZHANG Ying，CHEN Huixiang.Representations of finite dimensional pointed Hopf algebras overZn［J］.Comm Algebra，2012，40（10）：3801－3821.

The simple Yetter－Drinfeld modules of one Hopf algebra

ZHANG Ying1，CHEN Huixiang2＊

（1.Sch of Sci，Huaihai Inst of Tech，Lianyungang 222005，China；2.Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China）

This paper studies the simple Yetter－Drinfeld modules of one class of finite－dimensional graded Hopf algebraH.Using the action of generators ofHon the simple Yetter－DrinfeldH－modules，the author gives the structures of all simple Yetter－DrinfeldH－modules and classifies them up to isomorphism.

Hopf algebra；Yetter－Drinfeld module；simple Yetter－Drinfeld module

O 153.3

A

1007－824X（2015）04－0009－04

2015－06－28.＊ 联系人，E－mail：jsgyzy22＠sina.com.

国家自然科学基金资助项目（11171291）.

张颖，陈惠香.一类Hopf代数的单Yetter－Drinfeld模 ［J］.扬州大学学报（自然科学版），2015，18（4）：9－12.

（责任编辑 青 禾）