具时滞和细胞免疫的HIV－1模型稳定性分析

陈利君，胡志兴，廖福成

（北京科技大学数理学院，北京 100083）

具时滞和细胞免疫的HIV－1模型稳定性分析

陈利君，胡志兴＊，廖福成

（北京科技大学数理学院，北京 100083）

研究一类具时滞和两种细胞免疫（CTLp细胞和效应T细胞）的HIV－1病毒感染模型，讨论了无病平衡点E0和无免疫平衡点E1的局部稳定性，并证明了：1）当基本再生数R0＜1时，E0是全局渐近稳定的；2）当1＜R1＜R0时，时滞改变了免疫应答平衡点（正平衡点）E2的稳定性，并引起Hopf分支.

时滞；稳定性；基本再生数；Hopf分支；HIV－1病毒感染

艾滋病毒（HIV）已经成为危害人类健康的大敌，对其研究有着重要的意义.迄今为止，大量的数学模型被用于研究HIV病毒感染的问题，对病毒、宿主细胞之间相互关系的研究已取得很多的成果［1－3］.Nakata［4］研究了一类关于 Beddington－De Angelis（BD）发生率的三维 HIV－1模型，刘祥东等［5］研究了一类饱和感染率的HIV模型，Xiang等［6］研究了一类关于BD发生率和时滞的HIV－1病毒感染模型，Cai等［7］研究了一类非线性发生率的HIV－1病毒感染模型，Lv等［8］研究了一类关于效应细胞的五维HIV－1模型.基于以上研究，本文拟考察一类具非线性发生率、时滞和效应细胞的五维HIV－1模型，并对各个平衡点的稳定性进行分析.

1 模型的建立

本文研究如下一类具有时滞及细胞免疫的HIV－1病毒感染模型：

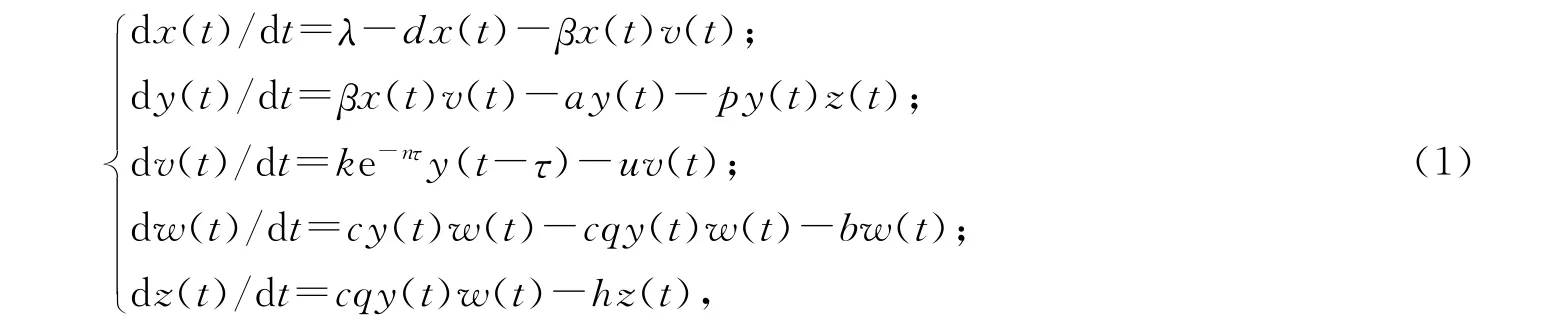
其中x（t）为靶细胞；y（t）为被感染细胞；v（t）为自由病毒数量；w（t）为 CTLp细胞数量；z（t）为效应T细胞数量；λ为常数，表示靶细胞产生率；d为常数，表示靶细胞死亡率；βx（t）v（t）为靶细胞变成感染细胞的发生率，β为常数；a为感染细胞的死亡率；p为常数，表示感染细胞被效应细胞清除率；k为感染细胞产生病毒率；u为病毒死亡率；c为免疫细胞产生率；q（0≤q＜1）为CTLp细胞转化为效应T细胞的转化率；b为免疫细胞的死亡率；h为效应细胞的死亡率；τ≥0为感染细胞产生病毒的时间，在τ时间内感染细胞产生病毒的存活率为e－nτ，这里n为常数；以上参数均大于等于0.

系统（1）的初始条件为：x（θ）＝φ1（θ）；y（θ）＝φ2（θ）；v（θ）＝φ3（θ）；w（θ）＝φ4（θ）；z（θ）＝φ5（θ），其中φi（θ）≥0（i＝1，2，…，5），θ∈［－τ，0）；φi（θ）＞0（i＝1，2，…，5），θ＝0.令φ＝（φ1，φ2，φ3，φ4，φ5）T∈C（［－τ，0］，R5＋），则φ是巴拿赫空间C（［－τ，0］，R5＋）中从［－τ，0］到 R5＋的连续函数，这里R5＋＝｛（x1，x2，x3，x4，x5）：x i≥0，i＝1，2，…，5｝.

2 平衡点及其稳定性分析

通过对系统（1）平衡点的分析，有如下结论.

定理1 在系统（1）中，i）总是存在无病平衡点E0＝（x0，0，0，0，0），其中x0＝d－1λ；ii）当R0＞1时，存在无免疫平衡点E1＝（x1，y1，v1，w1，z1），其中x1＝au／（kβe－nτ），y1＝du（R0－1）／（kβe－nτ），v1＝d（R0－1）／β，w1＝z1＝0；iii）当R0＞R1＞1时，存在一个免疫应答平衡点（正平衡点）E2＝（x2，y2，v2，w2，z2），其中x2＝λ／（d R1），y2＝b／［c（1－q）］，v2＝bke－nτ／［cu（1－q）］，w2＝ah（1－q）（R0－R1）／（pqbR1），z2＝a（R0－R1）／（p R1），式中R0＝λβke－nτ／（adu），R1＝1＋βbke－nτ／［cdu（1－q）］分别为病毒和CTL免疫基本再生数.

2.1 无病平衡点的稳定性分析

定理2 在系统（1）中，当R0＜1时，无病平衡点E0是局部渐近稳定的；当R0＞1时，E0是不稳定的.

证明 系统（1）在无病平衡点E0处的特征方程为

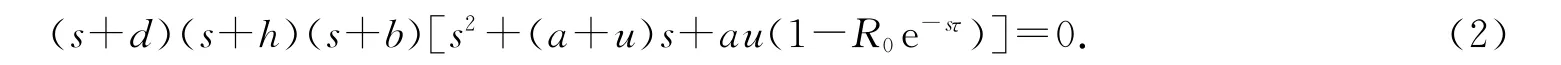
显然，（2）式有3个负实根：s1＝－d，s2＝－h，s3＝－b.于是判断（2）式根的情况，只须讨论方程

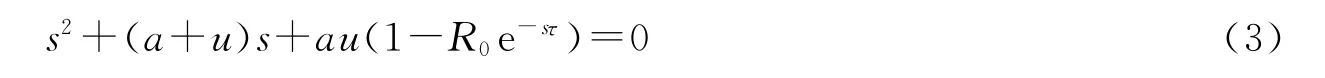
的根.当R0＜1时，由Routh－Hurwitz判据知，（3）式所有根均具有负实部；因此，当R0＜1时，无病平衡点E0是局部渐近稳定的；当R0＞1时，E0是不稳定的.

定理3 在系统（1）中，当R0＜1时，无病平衡点E0是全局渐近稳定的.

证明 设f：［0，∞）→R 为任意一个连续有界函数，定义f∞＝limt→∞supf（t），f∞＝limt→∞inff（t）.易知，当t≥0时，系统（1）满足给定初始条件的解都是非负且有界的；因此，对于每一个解，limt→∞sup和limt→∞inf均存在.由波动定理［9］知，存在一个时间序列tn→∞（n→∞），使得limn→∞x（tn）＝x∞，limn→∞x′（tn）＝0.由系统（1）中第1个方程可得dlimn→∞x（tn）＋βlimn→∞x（tn）·limn→∞v（tn）＝λ，故d x∞≤（d＋βv∞）x∞≤λ，即x∞≤d－1λ.同理，可得ay∞≤（a＋pz∞）y∞≤βx∞v∞，uv∞≤ke－nτy∞，bw∞≤c（1－q）y∞w∞，hz∞≤cqy∞w∞.下面用反证法证明v∞＝0.假设v∞＞0.由以上式子可得auk－1enτ（1－R0）v∞≤0，从而可知R0≥1，这与R0＜1相矛盾，故v∞＝0.又由v∞＝0，可得y∞＝w∞＝z∞＝0.又因0≤y∞≤y∞，故y∞＝0.同理可得w∞＝z∞＝v∞＝0，即limt→0y（t）＝limt→0w（t）＝limt→0z（t）＝0.最后，由系统（1）中第1个方程可得limt→0x（t）＝d－1λ.证毕.

2.2 无免疫平衡点的稳定性分析

定理4 在系统（1）中，当1＜R0＜R1时，对任意τ≥0，无免疫平衡点E1是局部渐近稳定的；当1＜R1＜R0时，E1不稳定.

证明 系统（1）在无免疫平衡点E1的特征方程为

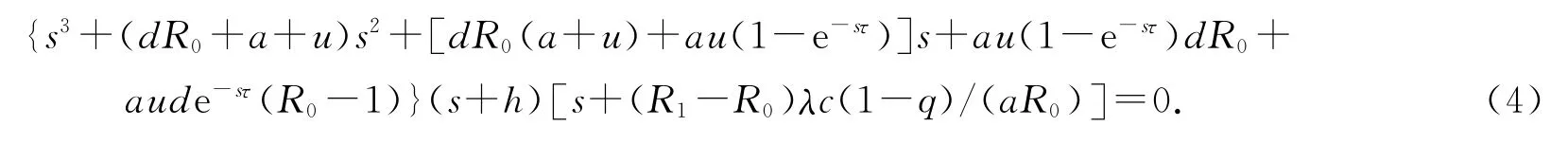
显然，（4）式有2个负实根：s1＝－h，s2＝－λc（1－q）（R1－R0）／（aR0）.欲判断（4）式特征方程所有根的情况，只须讨论方程

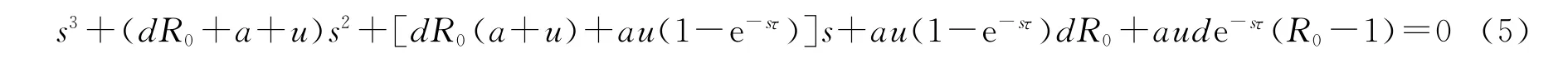
根的情况.当τ＝0时，（5）式可简化为

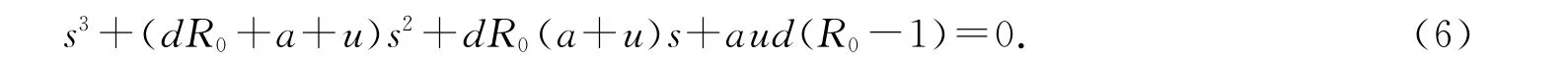
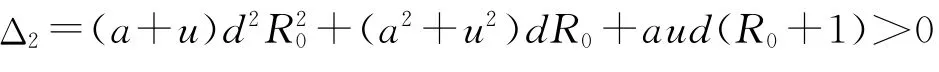
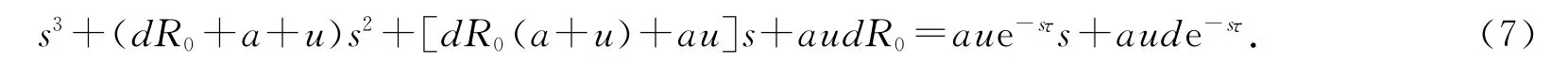
因s＝0不是（7）式的解，故不妨设s＝iω（ω＞0）为（7）式的一个解，则有

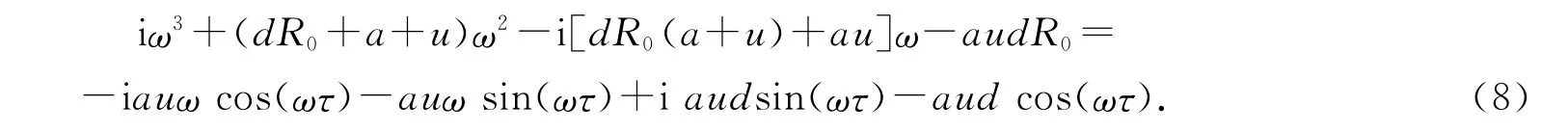
将（8）式分离实部和虚部，并平方相加可得

2.3 免疫应答平衡点（正平衡点）的稳定性分析

当1＜R1＜R0时，无免疫平衡点E1不稳定，故讨论免疫应答平衡点E2的稳定性.为求解简便，进行如下变化：

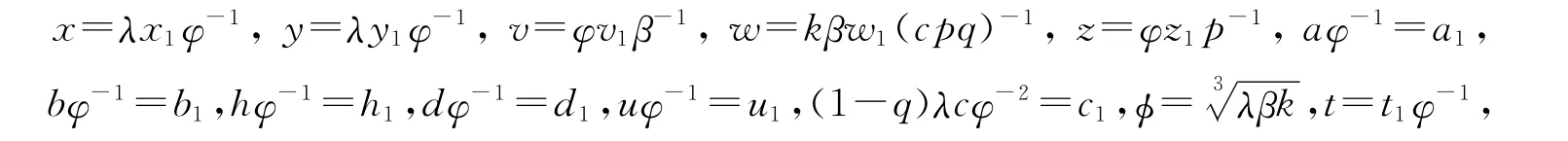
则系统（1）可转化为

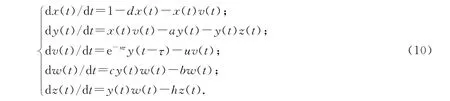
于是，R0＝e－nτ／（adu），R1＝1＋be－nτ／（cdu），E2＝（d－1，bc－1，be－nτ（cu）－1，ahc（R0－R1）（bR1）－1，a（R0－R1））.系统（10）在免疫应答平衡点E2的特征方程为

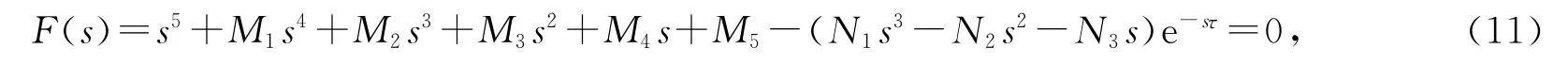
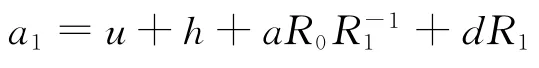
定理5 当1＜R1＜R0，τ＝0时，若Δ4＞0，则免疫应答平衡点E2是局部渐近稳定的.

讨论Hopf分支存在的条件，令τ＞0.假设s＝iω（ω＞0）是（11）式的一个根，并将其代入（11）式可得

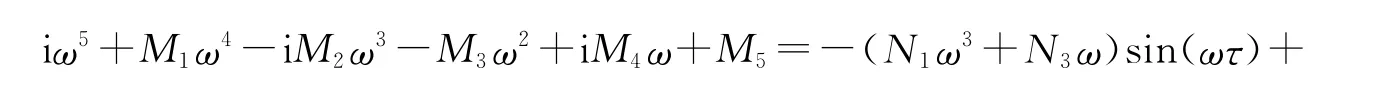
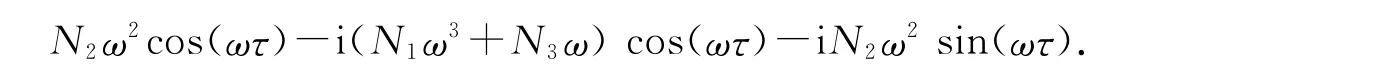
将该式实部和虚部分离，并整理得

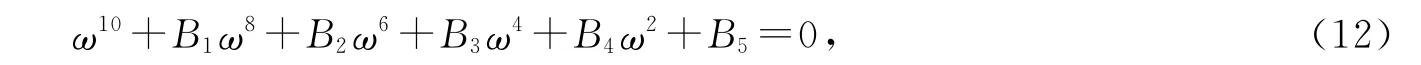
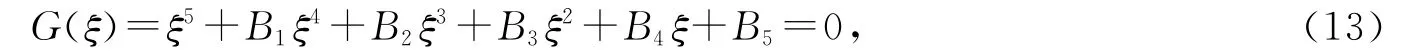
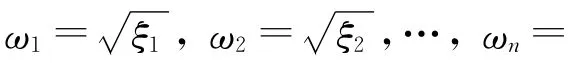
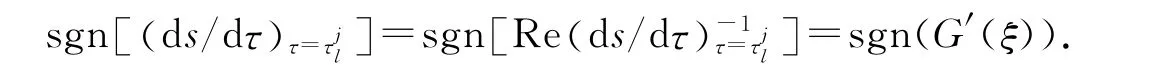
于是，由定理5和Hopf分支定理可得如下定理.

定理6 当1＜R1＜R0，Δ4＞0，G′（x）＞0时，假设（13）式至少有一个正根，则无免疫平衡点E2在τ＝τ0处产生Hopf分支，其中

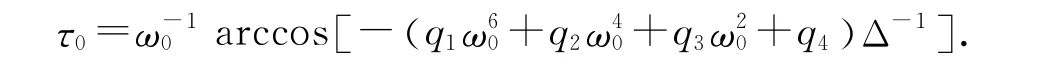
当τ＜τ0时，无免疫平衡点E2是稳定的；当τ＞τ0时，正平衡点E2是不稳定的.

3 结论

本文研究了一类关于靶细胞、被感染细胞、自由病毒、免疫细胞、效应细胞之间相互作用的HIV－1病毒感染模型.在此模型中，考虑了感染细胞产生病毒引起的时滞；分析了HIV－1病毒感染模型在不同情况下各个平衡点的稳定性：当R0＜1时，无病平衡点E0是全局渐近稳定的；当1＜R0＜R1时，对任意τ≥0，无免疫平衡点E1是局部渐近稳定的；当R0＞R1＞1时，时滞τ改变了免疫应答平衡点E2的稳定性，引起Hopf分支：若τ＜τ0，则E2是稳定的；若τ＞τ0，则E2是不稳定的.

［1］马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究 ［M］.北京：科学出版社，2004：259－268.

［2］ZHOU Xueyong，SONG Xinyu，SHI Xiangyun.Analysis of stability and Hopf bifurcation for an HIV infection model with time delay［J］.Appl Math Comput，2008，199（1）：23－38.

［3］HUANG Guang，MA Wanbiao，YASUHIRO T.Global analysis for delay virus dynamics model with Beddington－DeAngelis functional response［J］.Appl Math Lett，2011，24（7）：1199－1203.

［4］NAKATA Y.Global dynamics of a viral infection model with a latent period and Beddington－De Angelis response［J］.Nonlinear Anal，2011，74（9）：2929－2940.

［5］刘祥东，王辉，胡志兴，等.一类具有时滞和治愈率的HIV病理模型的稳定性 ［J］.生物数学学报，2011，26（1）：108－116.

［6］XIANG Hong，FENG Lixiang，HUO Haifeng.Stability of the virus dynamics model with Beddington－De Angelis functional response and delays［J］.Appl Math Model，2013，37（7）：5414－5423.

［7］CAI Liming，GUO Baozhu，LI Xuezhi.Global stability for a delayed HIV－1 infection model with nonlinear incidence of infection［J］.Appl Math and Comput，2012，219（2）：617－623.

［8］LV Cuifang，HUANG Lihong，YUAN Zhaohui.Global stability for an HIV－1 infection model with Beddington－DeAngelis incidence rate and CTL immune response［J］.Commun Nonlinear Sci Numer Simul，2014，19（1）：121－127.

［9］THIEME H R.Mathematics in population biology［M］.Princeton，NJ：Preceton University Press，2003：1－20.

［10］YU Pei，HUANG Jianing，JIANG Jiao.Dynamics of an HIV－1 infection model with cell mediated immunity［J］.Commun Nonlinear Sci Numer Simul，2014，19（10）：3827－3844.

The stability of an HIV－1 model with time delay and cell mediated immunity

CHEN Lijun，HU Zhixing＊，LIAO Fucheng

（Sch of Math ＆Phys，Univ of Sci ＆ Tech Beijing，Beijing 100083，China）

In this paper，the HIV－1 epidemic model with the cell mediated immunity and time delay is studied.Locally asymptotically stable of the infectious free equilibriumE0and the infectious equilibrium without CTLE1are discussed.It is proved that 1）if the basic reproductive numberR0＜1，E0is globally asymptotically stable.2）if the basic reproductive number 1＜R1＜R0，the stability of the infectious equilibrium with CTL responseE2is changed by using a delay as a bifurcation paramete，and therefore the Hopf bifurcation exists.

delay；stability；basic reproductive number；Hopf bifurcation；HIV－1 infection

O 175.14

A

1007－824X（2015）04－0019－05

2015－02－12.＊ 联系人，E－mail：huzhixing＠ustb.edu.cn.

国家自然科学基金资助项目（61174209）；北京科技大学冶金工程研究院基础研究基金资助项目（YJ2012－001）.

陈利君，胡志兴，廖福成.具时滞和细胞免疫的HIV－1模型稳定性分析 ［J］.扬州大学学报（自然科学版），2015，18（4）：19－23.

（责任编辑 青 禾）