从优秀走向优雅

2015-05-25黄金声

江西教育B 2015年4期

优秀的教师会不断地发展自己的教学技能，而当技能“进化”到技艺时，教师及课堂就从优秀走向了优雅。为此，许多教师在不断地探索着。笔者也尝试以“321实效课堂”为载体，试图立足于传统而后冲破其思维的禁锢，让课堂教学紧贴本位，以求得实效，从优秀走向高雅。

一、“321实效课堂”的基本理念

“321实效课堂”以“自主学习、互助探究、展示交流、教师点拨”为主线，构建课堂新秩序，强调课堂要从思维出发，发展学生思维能力。

1.理念“321”。三类优先：教育优先于教学，学优先于教，过程优先于结果。两个目标：做出色的自己，做重要的他人。一种体验：点燃他人，照亮自己，成就自己。

2.学法“321”。三自：自读，自探，自省。二议：议亮点，议盲点。一点拨：教师点拨。

3.教法“321”。三讲：想一想能懂的，慎讲；跳一跳能懂的，精讲；议一议不懂的，深讲。两种能力：运算能力，推理能力。一回头：反思。

4.学生“321”。三类问与不问：想一想能懂的，不问；跳一跳能懂的，慎问；议一议不懂的，必问。两种“1+1”组合：一帮一组合，交朋友；一追一组合，找对手。一种信念：永不放弃。

5.教师“321”。三种视角：跳出教育看教育；跳出教学看教学；跳出学科看学科。两种能力：娴熟的驾驭课堂能力，良好的处理偶发事件能力。一种境界：向学生学习。

6.试卷讲评“321”。三处讲起：从多数人的错误讲起，从刻骨铭心的错误讲起，从不可容忍的错误讲起。两次等待：让学生再做错题，先做后议。一个错题本：让学生准备一本错题本。

网络上有一个名为“35太难了”的教学视频，内容是一位小朋友在父母的逼问下背“1×5～6×5”的乘法口诀，起初总把3×5背成35，后来连其他当初能背出的口诀也背错了，这位小朋友哭诉“35太难了”的声音令人揪心。我们不禁要问：“35”真有这么难吗？是谁使“35”变得这么难的？“35太难了”折射出怎样的教育理念和教育现状呢？

其实，真正的教学不是背诵3×5，而是3×5为什么是15，又为什么不是35？回顾自己多年的教学经历，真是汗颜——我干过像“35太难了”这样的事有太多回了，真的需要改变课堂教学了。其实，课改不是很高深的东西。针对同样的教学内容，教师面对不同学生有不同的处理方法，面对相同学生的不同学习阶段也有不同的处理方法，这就是课改。从这个层面上看，每位教师都是课改的践行者。通俗地说，课改就是改课。改课不是对过去的否定，而是基于对传统继承后的不断修正、完善与发展，是为实现既定课程目标而做出思维方法的选择。

二、“321实效课堂”应把握的三个常规

当今教师承载的使命远不仅仅是传授知识这么简单，一个有智慧的教师应该有“教育优先于教学”的职业理念，让自己的职业行为由学科教学进入学科教育。从“学科教学”到“学科教育”是情感的渗入，是理念的跨越。教而不育，仅及皮毛，师生难以交心，“亲其师信其道”便要大打折扣。更有甚者，教师缺乏与学生的心灵沟通，凸显“情感漠视”，从而导致了教与学的双向缺失。因而要做到“321实效课堂”应把握的三个常规。

1.变管为理。教师是教学管理者，“管”是绕不开的一份责任。“管”的最高境界是“理”。

（1）理解学生的“负重”。做学生不容易，做个好学生更非易事。笔者经常回忆起自己做学生时的“坎坷”经历，并以此给学生借鉴和参考。

（2）理顺教学过程中的各个环节，使之精细化。教师应该知道自己和学生什么时候该做什么，怎么做；什么情况下先做什么，后做什么。比如错题本格式，笔者就推广黎瑾同学的做法：一是错题分析，包括错误答案及误区回顾等；二是共同分享，包括正确思路及有效拓展等。我们把它称为“黎瑾模式”。

（3）理性对待学生的学习困难。教师要本着“包容个性、尊重差异、相对成长”的原则，争做学生的“贴心人”。必须依靠学生，不断细化并完善每一个教学环节，关爱学生，让他们体验到学习的快乐。

2.变督为导。督为督促、督查，有催促、问责之意，教师用之无可非议。但若用得单一、频繁、不当，往往收效甚微，直至无效。

（1）指导。要转变思路，变学后督导为学前指导，帮助学生制定学习方案，明确学习策略，避免一些学习障碍。

（2）疏导。“321实效课堂”实施初始阶段，由于学生固有的行为习惯需要改变，新的学习习惯还未形成，不少学生还不适应。此时，教师应多一些肯定和鼓励，少一些批评和指责，尽己之力，做学生学习的向导，找出不足，不断反思，化解学生疑难。

（3）诱导。教师要让学生相信自己的能力，同时与学生一起设置阶段性学习目标，由易到难，层层深入，通过情景诱导、问题诱导、方法诱导、目标诱导等，不断激发学生的学习热情。比如在课堂展示交流环节，鼓励学生“不拘小节”：站着、坐着、吼着等均可为之，为的是要充分表达自己的观点，宣泄自己的情感，在思维的激烈碰撞中达成一致。

3.变惩为治。惩有惩罚、惩戒、惩处之意。有人认为，惩是为了治，严惩更是为了好治，更有甚者把惩当成治。当教育已经进入惩的阶段时，就意味着以前的管理失效；而当惩而无效时，教育者则无路可退，可基本认定为管理失败。笔者认为治才是纠错、改正乃至改进之道。在笔者参与制定的课堂评价方案中，只有加分项，没有扣分项，就是充分运用教育等待，实施以治为本的教育策略。

（1）自治。自治需要通过自省来纠正偏离目标的行为，我要求学生每天问自己几个问题——今天，学习互动得好吗？还有什么没有解决的问题？明天，怎样去做得更好？

（2）互治。在课堂互动时，由学科小组长召集其成员就存在的问题进行充分的梳理、分析、讨论，直至解决。另外，笔者要求每位学生处一位最交心的朋友，找一位理想的对手，让朋友成为学习、生活的好伙伴，让对手成为学习、生活的好标杆。

（3）救治。针对某个学生存在的学习障碍，安排本组成绩好的学生进行一对一辅导，同时教师也适时参与其中，给予其适当的帮助。

三、“321实效课堂”的基本要求

“321实效课堂”是以“自主学习、互助探究、展示交流、教师点拨”为主线构建课堂新秩序，强调课堂要从思维出发。下面以“圆与圆的位置关系”为例做具体介绍。

1.自主学习。自主学习基本要求是：在上新课前阅读课本相关内容，独立完成课本习题及课前案，对不懂的地方做出标注；在课堂开始时独立完成课中案、课前案的基本内容。例如，在教学“圆与圆的位置关系”时，教师让学生回顾下列知识：

（1）直线AB与⊙O的位置关系如下图所示：

①它们的位置关系是：图甲，图乙，图丙。

②它们都是轴对称图形吗？如是，请分别在图中画出它们的对称轴，并指出对称轴与直线AB有怎样的位置关系。

（2）设⊙O的半径为r，圆心O到直线AB的距离为d，则d与r的大小关系分别是：

图甲，图乙，图丙。

学生认真阅读课本“圆与圆的位置关系”的内容，回答下列问题：

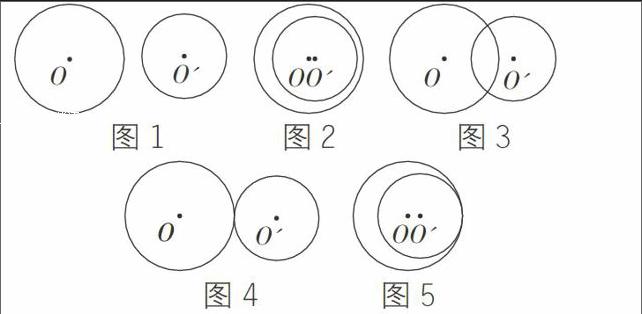
①如图，同一平面内两个不等圆之间的位置关系有以下5种，请分别写出其名称。

②图1～图5都是轴对称图形吗？如是，请分别在图中画出它们的对称轴.

自主学习是贯穿所有人一生的学习方式，也是人赖以生存、安身立命的基础。自主学习源于模仿，而后不断超越。就像运动员在正式比赛前要做热身准备一样，自主学习就是教师讲解前的热身，是学习的起始。自学能够提高学生在校学习的质量，而学习不理想的主要原因是自学能力不强。

依据其年龄所应有的正常心智水平，中学生已经具备这样的自学能力。自主学习对学生理解所学的知识很重要。正如要想听懂交响乐，就必须了解作者的思想及乐曲所描述主题的时代背景，同时还可以根据自己的生活经历、体验去理解交响乐，这样才能感受到它的意境、形象、情感，引起联想，受到感染。

2.互助探究。互助探究不仅在课堂，如有必要，在课前、课后均可进行。

课前：完成对课本疑难点的互动探究。具体为核对课本习题的答案，解答组内成员对课本问题的疑难问题。若有困难，可寻求教师或学习小组其他成员的帮助。

课中：一是核对课前案和课中案中问题的解答，讨论课中案中的疑难问题，若仍有困难，可在课中当场提出；二是共同分享各自的学习亮点。

课后：一是完成对教师批改后的课后案及测试卷中存在的问题的互动探究；二是对其他可能的问题互动探究。

在课中案中有这样一个问题：如“课前案”图1～图5，设圆心距为d，⊙O的半径为R，⊙O'的半径为r，问：d与R和r分别具有怎样的数量（大小）关系？（用等式或不等式分别表示出来）反之，能否用d与R和r之间的数量关系来判断两圆的位置关系？

此问题与“课前案”遥相呼应，通过互助探究，给完成“课前案”有困难的学生一个再认知的时间和机会，同时暗示“互逆现象”在数学命题间的广泛存在，并学会用线段图法探究此类问题。

互助探究就是让全体学生积极主动地参与到学习活动中来。只有互动，才能互助。为此，我们要改变传统课堂中的两个唯一：讲台是课堂的唯一中心，教师是学生的唯一中心。

3.展示交流。展示交流就是把学生的自主学习和互助探究的成果公开化。在课中案中有这样一个拓展问题设计：

准备一张圆形纸片，将圆的一部分向内折叠，得折痕AB（AB即为圆的一条弦），连接OA，OB，得△OAB，如图6～图9。

1.△OAB是何种特殊三角形？

2.如图10∽图11，随着折痕AB不断变长，∠AOB的度数也在不断地发生变化。已知⊙O的半径为R，设∠AOB=α。

①当AB在什么范围时，α为锐角？②当AB在什么范围时，α为钝角？③如图11，当AB为何值时，α=60°？④如图12，当AB为何值时，α=90°？⑤如图13，当弧AB经过点O时，α值是多少？∠MAN的度数是多少？⑥猜想：弧AB的长与α之间存在怎样的函数关系？

教师通过折圆的问题情境，将圆的一部分向内折叠，使研究对象从一个圆转化为两个圆（等圆），问题自然、清新、优雅，为学生展现探究问题的新角度，培养学生有效地认识问题本质的能力。通过展示交流，学生不仅再现了小学圆和弧的知识和初二函数的知识，又为下一节新课“弧长及扇形的面积”打下伏笔和基础，同时让学生感悟问题探究的方法，使学生逐步实现从掌握解题技巧到知晓思想方法的跨越，向“复杂的问题简单化、简单的问题深刻化”这一目标靠拢。

4.教师点拨。课堂的另一主体应该是教师，所以教师之于学生的学习是不可或缺的。如笔者提出了一个问题：“同一平面内两个不等的圆之间的位置关系”这句话中有两个限制条件，你能把它们找出来吗？为什么要有这两个限制条件？通过提问式的点拨，指导学生有效阅读，探寻“等圆”的特殊位置关系，渗透“从特殊到一般”的思想方法。

从优秀走向优雅，不仅是课堂教学的追求，也是每一位教师的教育追求。做一位有思想的教师，在课堂上传递一种态度，也许能让受众与自身的心灵泛起些许涟漪，而这正是我们教师的价值所在。

黄金声 “旋转中的特殊到一般”教学设计片段

从特殊到一般（包括从一般到特殊）是人们认识世界的基本思想方法之一，这一思想方法在数学的认识活动中有着重要的应用。本课例试图给出几何问题的一种探究思路，在深度解读问题背景中的一种基本数学思想——从特殊到一般的同时，强调课堂要从学生思维出发，促进学生思维能力发展，从而构建课堂教学新秩序。

【片段一】投石问路，激发动机

【问题1】将线段AB绕点A逆时针旋转60°得到线段AC，继续旋转得到线段AD，连接CD，BD，如图1。

（1）设∠BAC为α，若α=80°，则∠BDC的度数为__________；

（2）在第二次旋转过程中，若角α的度数变化，请探究∠BDC的大小是否改变。若不变，请求出∠BDC的度数；若改变，请说明理由。

生1：在第（1）问中 ∠BDC=30°，

在第（2）问中，∠BDC不变。

∠BDC=∠ADC-∠ADB==30°。

师：这是一种基于问题本质的解法，随着学习的不断深入，我们要不断发展自己的数学思维，正如我们在做“3+3”时，不必总是从基本的“1+1”开始。同学们想一想，还有更好的解题思路吗？

生2：以A为圆心，AB为半径作圆，B，C，D在同一个圆上，这样∠BDC与∠BAC就是同弧上的圆周角和圆心角。所以∠BDC=∠BAC=30°。