大地电磁二维正演中的无网格局部径向基点插值法

何建设，李俊杰＊，严家斌

（1．浙江省水利水电勘测设计院，杭州 310002；2．中南大学地球科学与信息物理学院，长沙 410083）

大地电磁二维正演中的无网格局部径向基点插值法

何建设1，李俊杰1＊，严家斌2

（1．浙江省水利水电勘测设计院，杭州 310002；2．中南大学地球科学与信息物理学院，长沙 410083）

无单元Galerkin法作为较成熟的一种无网格方法，已成功应用于有限元法触及的领域，还解决了如大变形、裂纹扩展及高速冲击等网格方法较难处理的问题，但其最大的缺陷在于系统方程的离散需借助背景网格，因此该方法并非真正意义上的无网格方法。无网格局部径向基点插值法采用子域法构造系统方程，加权残量只要求在局部积分域消除，大大降低了对背景网格的依赖，向真正的无网格迈进了一大步．这里将此方法用于大地电磁二维正演，介绍了该方法的基本原理；从大地电磁二维边值问题出发，利用子域法推导了与之对应的无网格局部弱式系统方程，并用高斯积分将其离散化；论述了局部径向基点插值法较无单元Galerkin法及有限元法的优缺点；最后通过二维模型的计算验证了算法的有效性。

局部径向基点插值法；大地电磁；无单元Galerkin法；有限元法

0 前言

正演是研究大地电磁的基础，高维问题的大地电磁场响应不存在解析解，为此须借助数值方法。有限单元法、有限差分法、积分方程法作为地球物理电磁法领域常用的网格方法，其最大缺陷在于求解复杂模型时网格生成困难。无网格法利用加权残量法构造求解问题的弱式（积分）形式或配点（微分）形式，并通过支持域内的节点构造形函数及建立离散系统方程，是一种基于节点的数值方法。因其无网格、精度高、模型加载便利等优点，成为了计算力学领域的研究热点，在地球物理学领域也有少量应用，报导的文献主要集中于无网格全域弱式Galerkin法［1－5］。

局部径向基点插值法（local radial point inter-polation method，LRPIM）［6－7］作为无网格弱式方法的一种较全域弱式无网格法（如无单元Galerkin法（Element-free Galerkin method，EFGM）［8－10］、点插值法（point interpolation method，PIM）［10－11］）其最大的改进在于数值积分只在局部积分域上进行，不涉及背景网格的生成，因而向真正的无网格法迈进了一大步。这里介绍了LRPIM的基本原理及大地电磁二维问题的LRPIM求解过程，通过两个二维模型的计算，证明了算法的有效性及其在处理复杂模型问题上的优越性。

1 局部径向基点插值法相关参数

LRPIM利用位于积分点支持域内的场节点构造形函数，数值积分在局部积分域上进行，因此先介绍支持域及积分域的概念。图1为LRPIM支持域、积分域、积分点与场节点示意图，由于局部积分域积分常选用高斯积分法，故积分点又称高斯积分点或高斯点。

图1 LRPIM支持域、积分域、积分点与场节点示意图Fig．1 Support domain，quadrature domain，gauss points and nodes in LRPIM

支持域与积分域情况如图1所示，常用的支持域及积分域形状有圆形与矩形两种，对于任一高斯点Χ，其支持域尺寸d及积分域尺寸dq由式（1）确定。

式中：α与αq为支持域及积分域的无量纲尺寸，它们用于控制实际支持域与积分域的大小，它们都是对LRPIM计算精度有显著影响的重要参数［7］；dc为位于高斯点Χ附近的平均结点间距，可由式（2）确定。

式中：A为预估的支持域面积；n为包含在A中的节点数。对于节点均匀分布的情况，dc为节点间距。这里采用矩形支持域，故有两个方向的支持域尺寸即式（3）。

式中：dcx与dcy分别为横纵向节点间距；αx与αy为对应的支持域无量纲尺寸。为便于程序设计，研究中常取αx＝αy＝α。

2 局部径向基点插值算法

取走向为Z轴，X轴与Z轴垂直，Y轴垂直向上，求解域为矩形区域，四个顶点依次以ABCD顺时针编号，Γ1为地质体与周围介质的边界。

当平面电磁波以任何角度入射地面时，地下介质中的电磁波总以平面波形式几乎垂直地向下传播，当地下电性结构为二维时，满足如下的边值问题［12］：

式中：ω为角频率；μ为磁导率；σ为电导率；ε为介电常数。

2．1 局部径向基点插值弱式方程

采用LRPIM构造的系统方程，加权残量要求在局部积分域Ωq上消除即

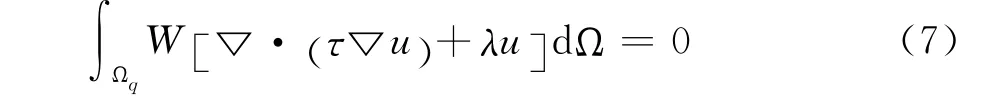
式（7）中：W是以节点为中心的权函数，与全域Galerkin弱式法不同，LRPIM权函数W与试函数u一般取自不同的函数空间，权函数取四次样条函数。式（7）可展开为式（8）的形式。

式（9）在边界Γ上代入式（4）所述的边界条件可得式（10）。

式（10）即为与大地电磁二维边值问题对应的LRPIM系统方程。

2．2 无网格离散系统方程的构造

求解式（10）需先将其离散，将场量u表示为节点处场量值与形函数之积的形式有

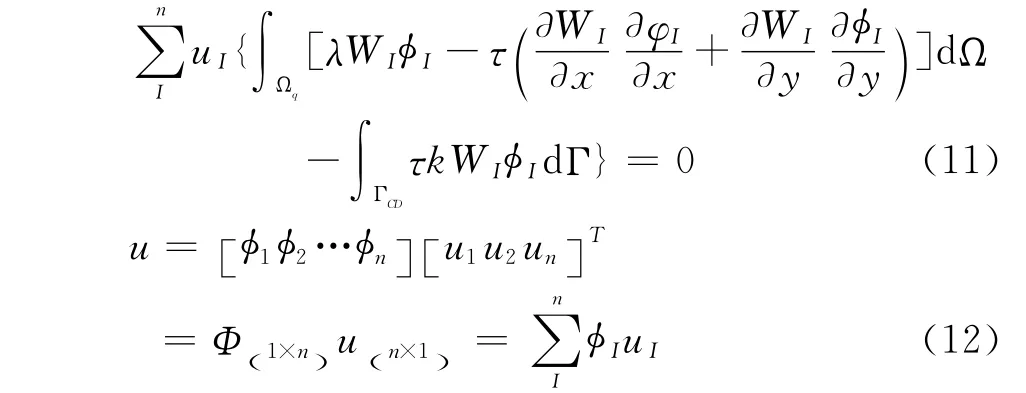
式（12）中的Φ为用径向基点插值法［6－7，13－15］构造的形函数，其近似原理如式（13）。

式中：Ri（x，y）为MQ（multi－quadrics）函数；p（X）为用Pascal三角形确定的基函数；a与b是系数向量；n为RBF的个数，m为单项式的个数；dc为与节点间距有关的特征长度，当节点均匀分布时可取dc＝；x与y为高斯点位置的坐标，xi与yi为支持域内节点的坐标；αc与q为对LRPIM计算精度有较大影响的形状参数，一般通过数值试验获得，文中取αc＝2．0，q＝0．5。

式（11）采用支持域内n个场节点编号，对于求解域内所有场节点还应有一个用于将局部节点矩阵组装成总体刚度矩阵的总体编号体系，即从1到N编号，因此式（11）变为式（14）。

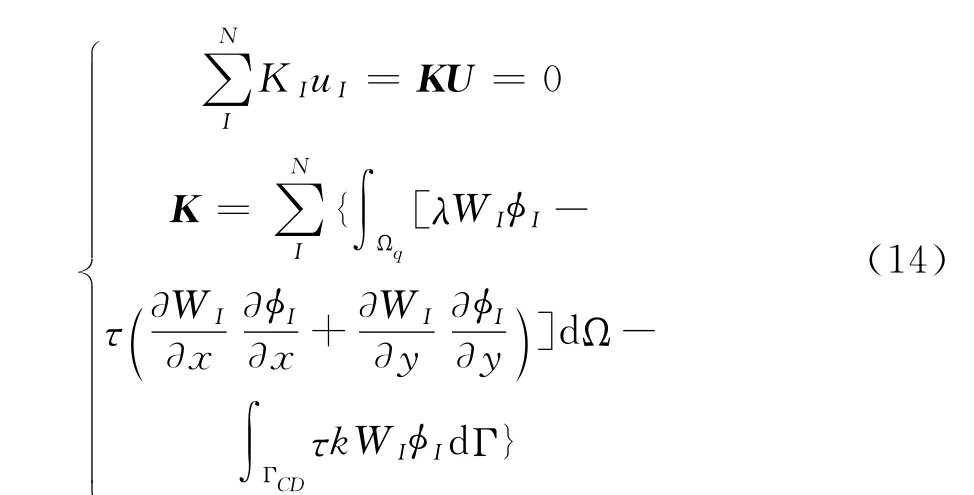
值得说明的是，LRPIM总体矩阵K的加载与无网格全域Galerkin弱式法及传统有限单元法不同，在FEM与全域Galerkin弱式法中，单元矩阵或节点矩阵是被系统地累加进总体矩阵的，而在LRPIM中，节点矩阵是按行摆放而形成总体矩阵的。

2．3 局部积分域数值积分

式（14）中K表达式中包含的局部积分，可利用高斯积分法求解有

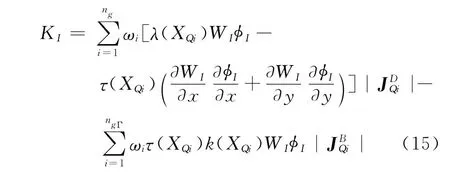
式中：ng与ngΓ分别为局部积分域及边界域上的高斯点数目；ωi为第i个高斯点XQi的权系数；与为对应的雅可比（Jacobian）矩阵。

LRPIM构造的总体矩阵K具有带状、稀疏的性质，但却是非对称的。非对称性主要是因为LRPIM表达式采用不同的函数构造试函数和权函数［16］。总体矩阵的不对称性增加了计算耗时，这也是LRPIM的主要缺陷。

求解线性方程组KU＝0还需加载边界条件，常用边界条件的加载方法有罚函数法［4－5］和Lagrange乘子法［8］。由于LRPIM形函数满足Kronecker delta函数特性（Ni（X）＝δij），边界条件也可直接加载［7］。

3 正演计算

为了研究算法的应用效果，计算了二维模型（图2）：模型一为正方形，背景电阻率为1 000 Ω·m，异常体电阻率为100Ω·m，边长为400m，异常体顶部到地面的距离为800m；模型二为圆形，半径为200m；模型三与四为椭圆，长半轴为300 m，短半轴为200m，前者为直立椭圆，后者为水平椭圆。计算时采用1 681（41×41）个场节点，节点等间距分布于问题域。

图3为频率f＝100Hz时模型一的数值计算结果，由图3可知，LRPIM计算结果与FEM及另两种全域Galerkin弱式无网格方法（EFG、PIM）一致，视电阻率与视相位曲线均很好地反映出了方形异常体的存在，证明了LRPIM求解大地电磁二维问题的有效性。

无网格法是一类基于节点的数值算法，其模型参数的加载基于高斯积分点而非单元，高斯点的位置可由坐标确定，该特性使其在复杂模型的构建上较常规网格方法方便。图4为模型二的无网格法计算结果，由图4可知，三种方法的异常曲线只在里程0km附近有细微的差别，均较好地反映出了异常体的存在，LRPIM异常幅值较其余两种无网格全域弱式法大。

图5为模型三与四的视电阻率计算结果，LRPIM与EFG、PIM计算结果基本一致，但曲线更窄，里程0km附近水平椭圆异常幅值较直立椭圆大（图5）。

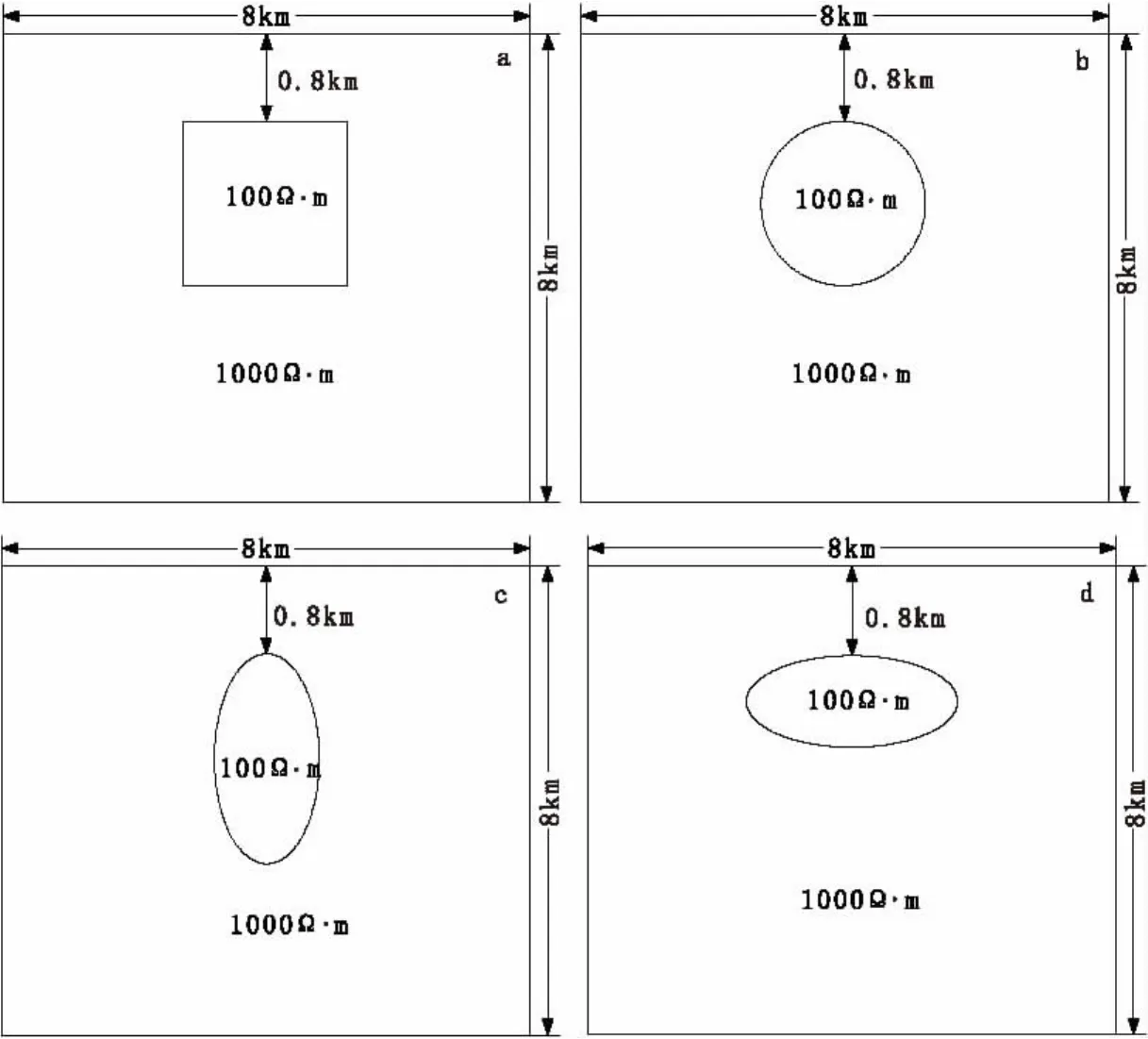
图2 二维理论模型Fig．2 Two－dimensional theoretical models

图3 频率f＝100Hz时模型一数值计算结果Fig．3 Numerical solutions of model 1when frequency is 100Hz

4 结论

1）将LRPIM应用于大地电磁二维正演，介绍了无网格法中相关参数（支持域、积分域、高斯积分点）的基本概念。

2）从大地电磁二维边值问题出发，采用子域加权残量法结合高斯积分公式，推导出了与之对应的LRPIM系统方程及总体矩阵表达式。

3）截面方形二度体模型的LRPIM计算结果与FEM一致，验证了LRPIM在大地电磁二维正演中的有效性。复杂地质模型电磁响应的计算一般需采用非结构化网格，此种网格的生成算法较复杂。作者采用节点规则分布的LRPIM计算了圆与椭圆二维模型的电磁响应，计算结果较好地反应出了异常体的存在，体现了LRPIM在计算复杂模型上的优越性。

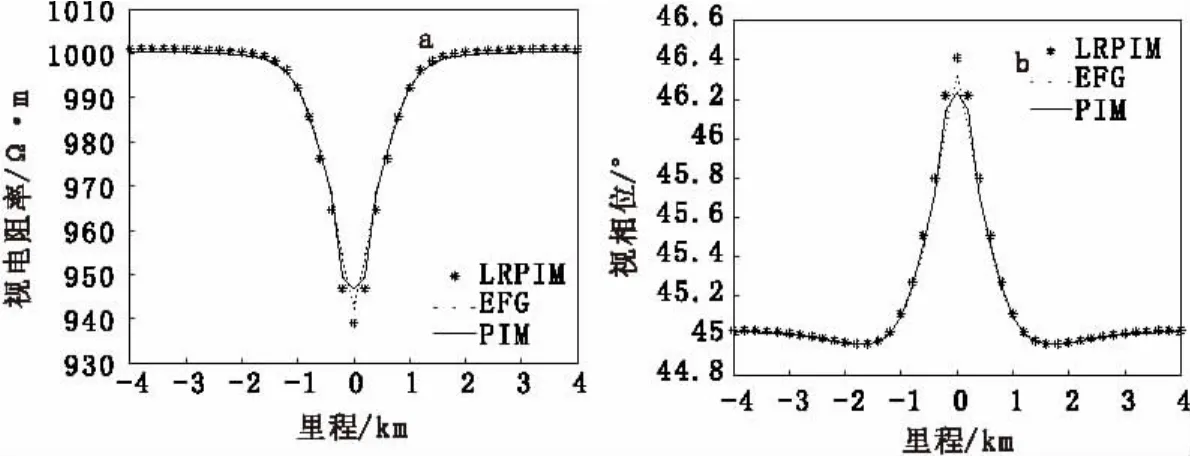
图4 频率f＝100Hz时图模型二数值计算结果Fig．4 Numerical solutions of model 2when frequency is 100Hz

图5 频率f＝100Hz时图模型三与模型四的视电阻率数值计算结果Fig．5 Numerical solutions of apparent resistivity for model 3and model 4when frequency is 100Hz

［1］贾晓峰，胡天跃，王润秋．复杂介质中地震波模拟的无单元法［J］．石油地球物理勘探，2006，41（1）：43－48．

JIA X F，HU T Y，WANG R Q．A mesh－free algorithm of seismic wave simulation in complex medium ［J］．Oil Geophysical Prospecting，2006，41（1）：43－48．（In Chinese）

［2］王月英．地震波正演模拟中无单元Galerkin法初探［J］．地球物理学进展，2007，22（5）：1539－1544．

WANG Y Y．Study of element－free Galerkin method in the seismic forward modeling［J］．Progress in Geophysics，2007，22（5）：1539－1544．（In Chiness）

［3］冯德山，王洪华，戴前伟．基于无单元Galerkin法探地雷达正演模拟［J］．地球物理学报，2013，56（1）：298－308．

FENG D S，WANG H H，DAI Q W．Forward simulation of ground penetrating radar based on the element－free Galerkin method［J］．Chinese Journal of Geophysics，2013，56（1）：298－308．（In Chinese）

［4］严家斌，李俊杰．无网格法在大地电磁正演计算中的应用［J］．中南大学学报：自然科学版，2014，45（10）：3513－3520．

YAN J B，LI J J．Magnetotelluric forward calculation by meshless method［J］．Journal of Central South University：Science and Technology，2014，45（10）：3513 －3520．（In Chinese）

［5］李俊杰，严家斌．无网格点插值法大地电磁二维正演数值模拟［J］．石油物探，2014，53（5）：617－626．

LI J J，YAN J B．Magnetotelluric two－dimensional forward numerical modeling by meshfree point interpolation method［J］．Geophysical Prospecting for Petroleum，2014，53（5）：617－626．（In Chinese）

［6］LIU G R，GU Y T．A local radial point interpolation method（LRPIM）for free vibration analyses of 2－D solids［J］．Journal of Sound and Vibration，2001，246 （1）：29－46．

［7］LIU G R，YAN L，WANG J G，Gu Y T．Point interpolation method based on local residual formulation u-sing radial basis functions［J］．Structural Engineering and Mechanics，2002，l4（6）：7l3－732．

［8］BELYTSCHKO T，LU YY，GU L．Element－free Galerkin methods［J］．International Journal for Numerical Methods in Engineering，1994，37（2），229－256．

［9］李俊杰，严家斌．无网格法进展及其在地球物理学中的应用［J］．地球物理学进展，2014，29（1）：452－461．

LI J J，YAN J B．Developments of meshless method and applications in geophysics［J］．Progress in Geophysics，2014，29（1）：452－461．（In Chinese）

［10］李俊杰．基于弱式无网格法的大地电磁二维正演［D］．长沙：中南大学，2014．

LI J J．Magnetotelluric two－dimensional forward by weak－form meshfree methods［D］．Changsha：Central South University，2014．（In Chinese）

［11］LIU G R，GU Y T．A point interpolation method for two－dimensional solids［J］．International Journal for Numerical Methods in Engineering，2001，50（4）：937 －951．

［12］戴前伟，张富强，杨坤平，等．电导率分块线性变化的二维高频大地电磁法有限元正演模拟［J］．物探化探计算技术，2012，34（5）：552－558．

DAI Q W，ZHANG F Q，YANG K P，et al．The finite element method for modeling 2－d high－frequency electromagnetic with continuous variation of conduc-tivity within each block［J］．Computing Techniques for Geophysical and Geochemical Exploration，2012，34 （5）：552－558．（In Chinese）

［13］WANG J G，LIU G R．A point interpolation meshless method based on radial basis functions［J］．International Journal for Numerical Methods in Engineering，2002，54（11）：1623－1648．

［14］李莹，夏茂辉，董凯．无网格局部径向点插值法求解Helmholtz方程［J］．郑州大学学报：理学版，2012，44 （4）：26－30．

LI Y，XIA M H，DONG K．A meshless local radial point interpolation method for the Helmholtz equation ［J］．Journal of Zhengzhou University：Natural Science Edition，2012，44（4）：26－30．（In Chinese）

［15］严默非，杨庆，常文洁．局部径向基点插值法模拟裂纹尖端附近应力场［J］．武汉理工大学学报，2010，32 （5）：141－145．

YAN M F，YANG Q，CHANG W J．Local radialbasis point interpolation method for crack tip stress field［J］．Journal Of Wuhan University of Technology，2010，32（5）：141－145．（In Chinese）

［16］ATLURI S N，KIM H G，CHO J Y．A critical assessment of the truly meshless local Petrov－Galerkin （MLPG）and Local Boundary Integral Equation （LBIE）methods［J］．Computational Mechanics，1999，24（5）：348－372．

Two－dimensional forward of magnetotelluric using meshless local radial point interpolation method

HE Jian-she1，LI Jun-jie1＊，YAN Jia-bin2
（1．Zhejiang Design Institute of Water Conservancy and Hydroelectric Power，Hangzhou 310002，China；2．School of Geosciences and Info－Physics，Central South University，Changsha 410083，China）

Element－free Galerkin method（EFGM）as a relatively mature meshless method not only has been successfully applied in the field of where the finite element method（FEM）used，but also addressed many problems which grid method is difficult to deal with such as large－deformation，fracture and crack growth and high speed impact．Its biggest drawback is that discrete process of system equation involves the background grid generation therefore cannot be called the true sense of meshless method．Subdomain method is used to construct the system equation in meshless local radial point interpolation method （LRPIM），the weighted residual only be demanded eliminating in local integral domain greatly reduces the dependence on the background grid therefore LRPIM forwards a major step to the true meshless method．This paper devotes two－dimensional magnetotelluric forward by LRPIM and its basic principle is introduced．Weak form equation is derived by subdomain method corresponding to the magnetotelluric two－dimensional boundary value problem then the equation is discrete by gauss integral method．The advantages and disadvantages of LRPIM are analyzed comparing to EFGM and FEM．At last，the validity of the algorithm is verified by two－dimensional model calculations．

local radial point interpolation method；magnetotelluric；element-free Galerkin method；finite element method

P 631．3

A

10．3969／j．issn．1001-1749．2015．03．01

1001-1749（2015）03-0267-06

2014-08-01 改回日期：2014-10-13

国家自然科学基金（40874055）；湖南省自然科学基金（07JJ5065）

何建设（1970－），男，高级工程师，主要从事水电勘测与电磁法正演研究，E-mail：751141742＠qq．com。

＊通信作者：李俊杰（1989－），硕士，主要从事地球物理场无网格化正演研究，E-mail：838885421＠qq．com。