水平层状电各向异性介质大地电磁正演研究
2015-05-25刘鸿洲安亚婷
刘鸿洲,安亚婷
(中国地质大学a.构造与油气资源教育部重点实验室,b.资源学院,武汉 430074)
水平层状电各向异性介质大地电磁正演研究
刘鸿洲a,b,安亚婷a,b
(中国地质大学a.构造与油气资源教育部重点实验室,b.资源学院,武汉 430074)
电各向异性现象在地球内部是普遍存在的,通过理论上推导的电各向异性介质的张量电导率的表达式及水平层状电各向异性介质的大地电磁正演公式,对一些地电模型进行数值计算,同时与电各向同性地电模型进行对比分析。结果表明,电各向异性介质的张量电导率的大小不仅与介质的固有电阻率性质有关,还与测量的方向有联系;电各向异性系数和相对测量角的变化都对地层的视电阻率和相位曲线振幅有较大的影响,但其曲线形态基本保持不变;当野外观测方向和电各向异性介质的电性主轴重合时,电各向异性介质模型可以看成两个独立的电各向同性介质模型。这些结果有助于以后的电各向异性介质实验研究和其大地电磁反演研究。
张量电导率;大地电磁测深;电各向异性;正演研究
0 引言
常规大地电磁测深(Magnetotelluric,MT)往往假设地下介质为电各向同性。近年来随着地球物理技术方法的进展和地球认识的逐渐深入,地球的电各向异性问题越来越引起人们的关注,越来越多的证据[1-8]也表明:地壳和上地幔通常是电各向异性的,地球介质的物理性质(如弹性,导电性,磁性,导热性和密度等)存在明显的电各向异性,地球内部介质的电各向异性是地球科学的难点和前沿课题。MT法与其他方法(如地震)相比,其成本低、探测深度大,是地壳上地幔探测的主要方法之一,能很好地揭示出介质的电各向异性。
一维大地电磁电各向异性介质正演研究从上世纪60年代到如今已经发展了半个多世纪,国外有较成熟的研究,O'Brien等[9]及Reddy等[10]分别推导了层状电各向异性介质中电磁场的递推公式及研究了倾斜电各向异性对大地电磁场的影响;捷克学者Josef Pek[11]在前人的基础上推导了层状电各向异性介质中大地电磁阻抗张量表达式。在国内,石应骏[12]、陈乐寿[13]、林长佑[14]、阮爱国[15]、霍光谱[16]、周健美[17]等学者对电各向异性介质都进行了一些大地电磁正演研究,特别是霍光谱[18]对电各向异性介质的大地电磁正演进行了综述研究。这里主要在理论上推导了电导率张量产生的原理,从理论上解释了电导率张量的形式,并在此基础上系统地对水平层状电各向异性介质进行了大地电磁正演研究,完善了正演理论,分析了电各向异性系数、相对观测角对水平层状电各向异性介质的视电阻率和相位曲线的影响。这有助于电各向异性介质的大地电磁野外观测和其反演研究。
1 电各向异性介质张量电导率表达式
众所周知,在电各向异性介质中,一般Ji和Ei(i=x,y,z)的方向是不一致的。但是根据实验的结果[19],介质中存在几个特殊的方向,在这些方向上电流密度和电场方向是一致的,我们称这几个特殊的方向为电各向异性介质的电性主轴。为了数学推导方便,假设介质只有三个主轴并且它们之间互为正交并构成一个直角坐标系。用带撇的三个直角坐标轴x′、y′、z′表示所研究的电各向异性介质的三个主轴,而用不带撇的三个直角坐标系轴x、y、z表示观察者所在的直角坐标系中的三个坐标轴,两个直角坐标系的轴之间可以有任意的夹角θki(k =x′,y′,z′;i=x,y,z),θki表示k轴到i轴的夹角(顺时针旋转)。
1.1 电场Ex对电各向异性介质的作用
在观测者坐标系中,设有一个外电场E为:

因为观测者中x轴不在电各向异性介质的三个主轴上,故把Ex投影到三个主轴x′、y′、z′上(Exx′,Exy′,Exz′),并分别在电性主轴上产生电流密度Jxx′、Jxy′、Jxz′。表达式为:

其中σx′、σy′、σz′分别是主轴上的电导率,反应了电各向异性介质的固有电性性质。因为是在观察者所在坐标系中观察介质的电流密度,故应把外电场Ex在电各向异性介质三个主轴上产生不同方向的电流密度Jxx′、Jxy′、Jxz′分别投影到观察者所在的坐标系中的x、y、z轴上,所得的Jxx、Jxy、Jxz表达式为式(4)。

1.2 电场E对电各向异性介质的作用
根据Ex对电各向异性介质作用的理论,同理可以得到Jyx、Jyy、Jyz、Jzx、Jzy、Jzz的表达式(其表达式与Jxx,Jxy,Jxz的表达式相似)。最后用Jx、Jy、Jz表示外电场E在x、y、z轴上产生的电流密度:

把Jxx、Jxy、Jxz、Jyx、Jyy、Jyz、Jzx、Jzy、Jzz的表达式,代入公式(5),得到电流密度的张量表达式:

其中:

从上述公式可以看出,电各向异性介质的电导率是张量形式,其大小不仅与介质本身的性质(电性主轴的方向和其电导率的大小)有关,而且与野外数据采集时测量方向有关。
对于层状介质,电性主轴z是垂直于介质层面的,当电性主轴z′和测量z轴一致时,电各向异性介质的张量电导率可以简化成如下形式:
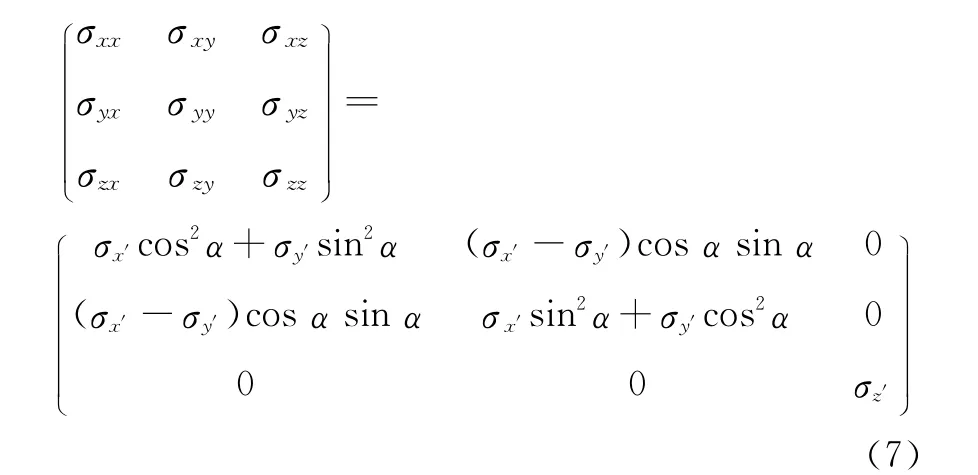
其中:σx′、σy′、σz′分别是介质主轴上的电导率;角度α定义为野外测量方向相对于地层电性主轴方向的夹角,即相对测量角。
2 大地电磁层状电各向异性介质正演理论
该理论部分借鉴于Josef Pek[11]在2002年发表的关于电各向异性介质正演的相关研究。
2.1 水平层状电各向异性介质中的大地电磁响应
假设有介质其前N层为电各向异性介质,N+1层为一个均匀无限半空间。电磁波是垂直入射到地层的平面波。从麦克斯韦方程组出发[20],根据在一维层状介质中的条件∂/∂x=∂/∂y≡0,联立公式(7),在笛卡尔坐标中,把麦克斯韦方程分解成如下:

并且有:

根据公式(8)和公式(9)整理得到一组关于电场的二阶耦合微分方程组:
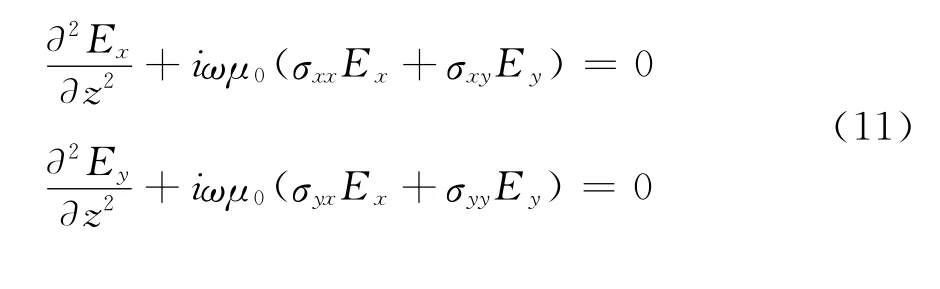
对于方程组的解,Ex、Ey解的形式应包含指数e±kz,且Ex、Ey都不是独立存在的,可以令Ex=QEy,容易得到在电各向异性介质中,总是存在两种解的模式,对应了两个不同的平面波:

若用主轴电导率表示k1,2有:(其中令σx′=σ1,σy′=σ2)

2.2 大地电磁电各向异性介质中的阻抗张量
根据方程组的解析解,可以将一个特定层中深度为z时的水平电磁场用矩阵方程表示:

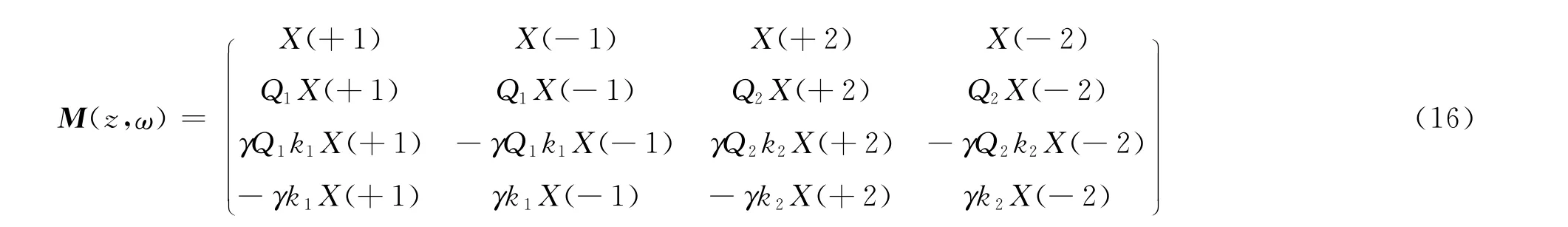

矢量D包含了在层状介质中两个下行波(D-1,D-2)和两个上行波(D+1,D+2)的振幅大小。在N+1层的均匀半空间,随着z→∞,上行波减小到零,所以在均匀半空间,只有下行波存在,即D+1,N+1=D+2,N+1=0。
由地层中的边界条件,得到在第l层中底部和顶部的大地电磁场有:Fl(zl,ω)=Fl+1(zl,ω),即:

其中:ζ1、ζ2、α是均匀半空间的参数。
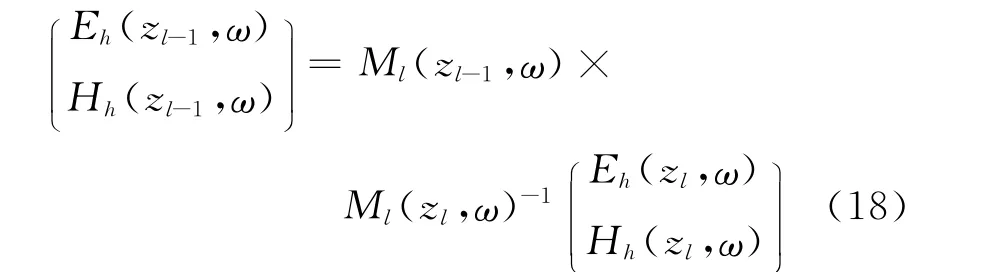
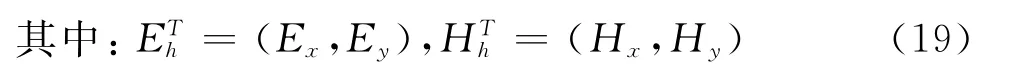
最后把阻抗定义式:Eh(z,ω)=Z(z,ω)Hh(z,ω)代入公式(18)得到阻抗张量的递推表达式:
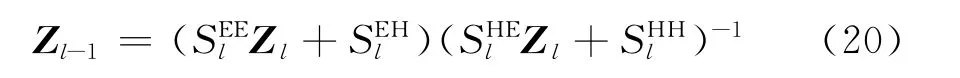
在特殊情况下,在均匀半空间中阻抗张量表示为式(21)。
3 水平层状电各向异性介质的模型算例
通过对一些电各向异性地电性模型做数值计算[21-22],并和电各向同性介质进行对比,可以研究大地电磁场在电各向异性介质的分布规律,并探讨电各向异性系数、相对观测角对视电阻率和相位曲线的影响。
3.1 两层电各向异性地电模型(模型一)
对一个简单的两层电各向异性地电模型做正演计算,研究其视电阻率的分布形态,模型参数为:h1=3km=10Ω·=1 000Ω·m,α=30°,ρ2 =1 000Ω·m,计算结果见图1。

图1 两层电各向异性介质视电阻率曲线图Fig.1 Apparent resistivity curves in anisotropic media layers
由图1可知,ρxy和ρyx包含了符合实际地电模型的有用信息,能比较直观地了解地层模型;ρxx和ρxy两值相等,但和ρxy、ρyx相差较大,不能较好地反应模型地层的电性结构,故这两个方向的视电阻率并不十分重要(在以后的模型正演中一般不显示这两个方向的视电阻率曲线)。总体来看,ρxy、ρyx两条曲线的趋势形态基本一致,但其值的大小存在着较大差别。在视电阻率曲线的低频区域,ρxy、ρyx两条曲线逐渐重合,这是因为第二层为电各向同性均匀半空间;在高频区域,两条曲线差别明显,这是因为第一层为电各向异性介质,水平的两个电性主轴的电导率不相等,且ρxy和ρyx的值介于两个电性主轴电阻率之间。
3.2 不同电各向异性系数下的地电模型正演对比(模型二)
地电模型的很多参数都会影响电各向异性介质正演的视电阻率、相位曲线。电各向异性系数m是纵向电导率σL与横向电导率σt比值的平方根,对三层电各向异性地电模型A进行正演计算,探讨了电各向异性系数对视电阻率、相位曲线的影响。电各向异性三层模型第一层为电各向同性介质地层,第二层为电各向异性介质地层,第三层为均匀半空间基底。设电各向异性系数的大小分别为0.1、0.5、1、1.5、2,相对测量角度为30°,具体参数见表1。计算结果见图2(因为ρxy和ρyx的形态基本一致,在探究电各向异性系数对曲线的影响时,以免累赘,仅以ρxy为例)。
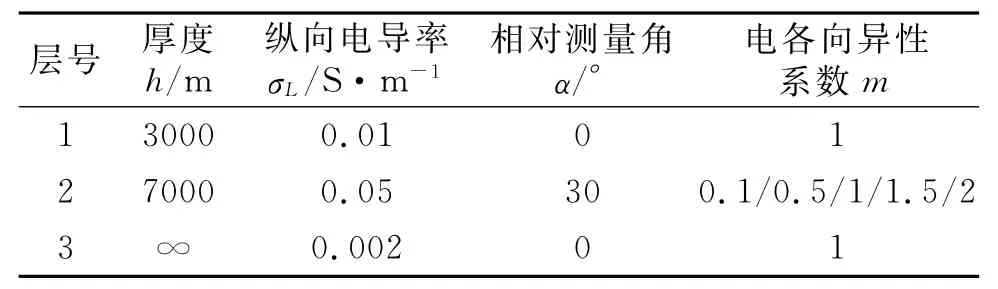
表1 模型A参数Tab.1 Parameter of model A
通过对视电阻率曲线和相位曲线的分析,得到在不同电各向异性系数情况下,视电阻率和相位曲线的形态基本保持一致,但在某一频率段对其值的大小影响很明显。如在模型A地层中,曲线在高频和低频曲线的差别很小,在频率10-3Hz~10-1Hz之间,曲线分离。
图2中红色星线表示的是模型A电各向异性系数为1的正演视电阻率和相位曲线图,此时模型A介质相当于一个各向同性的介质,和其他曲线对比发现,电各向异性介质和电各向同性介质的曲线差异很大,曲线中明显的差异性说明了大地电磁对于电各向异性是能够很好地区分的,且对视电阻率曲线影响很明显,在实际工作中,需要考虑地层的电各向异性性质,而不能仅假设地层为电各向同性。
3.3 不同相对测量角下的地电模型正演对比(模型三)
相对观测角度是指野外数据采集时,布线方向和地层的电性主轴方向的夹角,为了探究相对观测角度对视电阻率相位曲线的影响,同样对一个三层电各向异性地电模型B进行正演计算,并与另外两个三层电各向同性地电模型C、D的正演结果进行对比。电各向异性三层模型第一层为电各向同性介质地层,第二层为电各向异性介质地层,第三层为均匀半空间基底。设相对观测角度σ的大小分别为0°、30°、45°、60°、90°,具体参数见表2,计算结果见图3(同样仅以ρxy为例)。
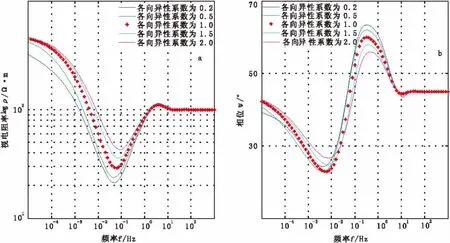
图2 不同电各向异性系数下模型A视电阻率、相位曲线图Fig.2 Apparent resistivity and phase curves in different anisotropic coefficients media model

表2 模型B参数Tab.2 Parameter of model B
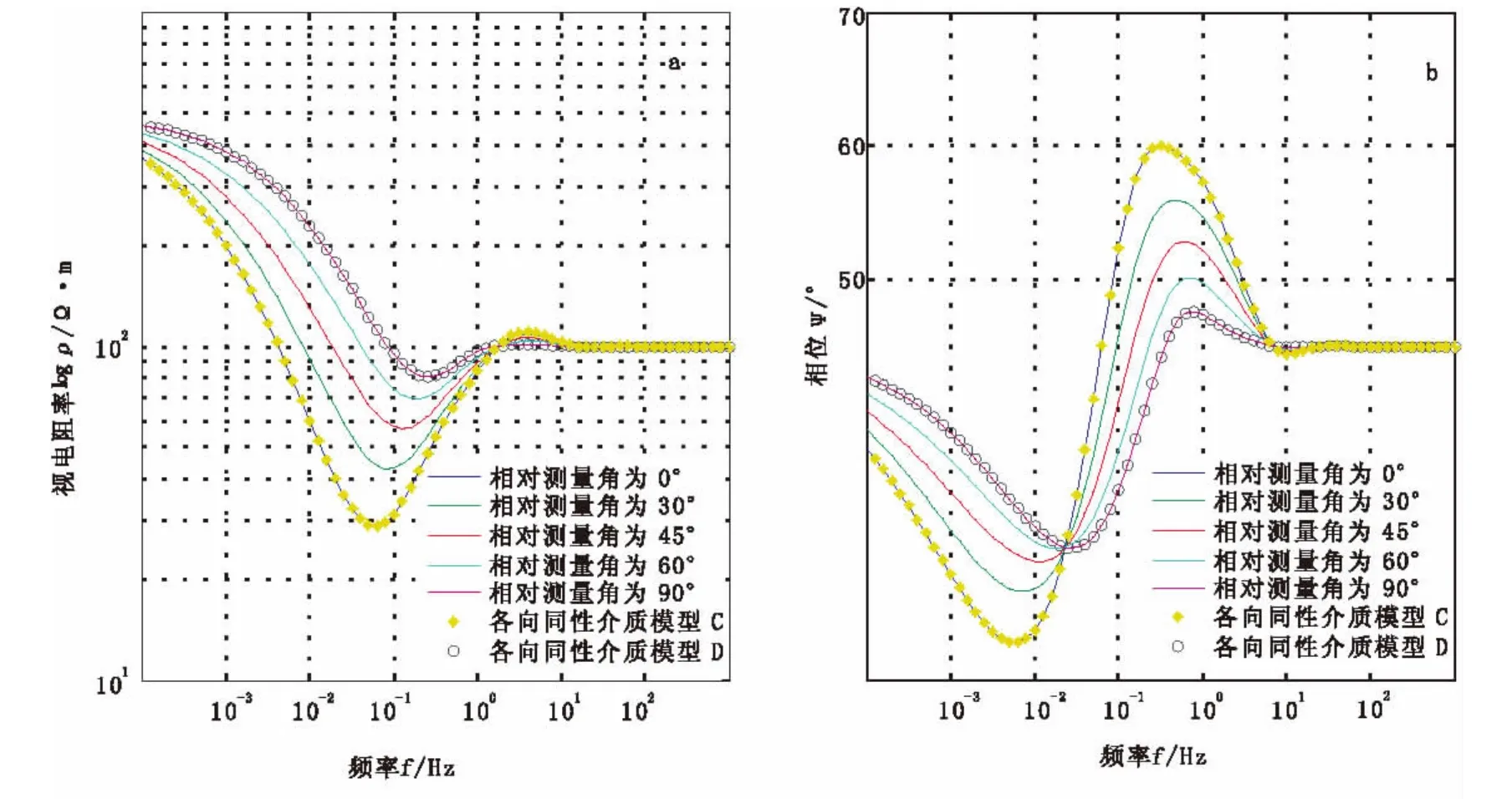
图3 不同相对测量角下视电阻率、相位曲线变化图Fig.3 Apparent resistivity and phase curves in different relative measuring angle media model
分析图3发现,视电阻率、相位曲线的形态基本一致,但视电阻率和相位曲线对相对测量角度的变化表现很敏感。由模型B与模型C、D对比发现,模型C、D的视电阻率相位曲线与模型B测量角分别为0°和90°的视电阻率相位曲线重合。模型C、D的参数基本相同,仅在中间层有差异,模型C中间层电导率为模型B的纵向电导率,模型D中间层电导率为模型B的横向电导率。结果说明,当野外观测方向和电各向异性介质的电性主轴重合时,电各向异性介质可以看成是两个电各向同性介质。

表3 模型C参数Tab.3 Parameter of model C

表4 模型D参数Tab.4 Parameter of model D
4 结束语
1)作者从理论上得到了电各向异性介质的张量电导率的表达式,其大小不仅与介质的固有电阻率性质有关,还与测量的方向有关。当电各向异性介质为水平层状且测量轴为笛卡尔坐标轴时,此时电导率张量的表达式有明显的变化。
2)电各向异性系数和相对测量角都对地层的视电阻率和相位曲线有较大地影响,但其基本形态基本保持不变。在野外观测中,这种介质的电各向异性对其视电阻率和相位的影响是不容忽视的。
3)当野外观测方向和电各向异性介质的电性主轴重合时,电各向异性介质模型可以看成两个独立的电各向同性介质模型。
[1]王家映.我国大地电磁测深研究新进展[J].地球物理学报,1997,40(1):206-216.
WANG J Y.New deverlopment of magnetotelluric sounding in China[J].Geophys,1997,40(1):206-216.(In Chinese)
[2]尹曜田.利用断裂带电阻率各向异性结构揭示区域构造演化过程的研究——以加拿大大奴湖韧性剪切带为例[D].北京:中国地质大学,2014.
YIN Y T.Regional tectonic evolution processes re-vealed from the electrical anisotropic structure of major shear zone:The case of the GSLsz,NW Canada[D].Beijing:China University of Geosciences,2014.(In Chinese)
[3]魏文博,谭捍东,金胜,等.华北中部岩石圈电性结构——应县—商河剖面大地电磁测深研究[J].地球科学:中国地质大学学报,2002,27(5):645-650.
WEI W B,TAN H D,JIN SH,et al.Conductivity structure of lithosphere in central north China:magnetotelluric study of Yingxian-Shanghe profile[J].Earth Science-Journal of China University of Geosciences,2002,27(5):645-650.(In Chinese)
[4]魏文博,金胜,叶高峰,等.藏北高原地壳及上地幔导电性结构[J].地球物理学报,2006,49(4):1215-1225.
WEI W B,JIN SH,YE G F,et al.Conductivity structure of crust and upper mantle beneath the northern Tibetan Plateau:Results of superwide band magnetotelluric sounding[J].Geophys,2006,49(4):1215 -1225.(In Chinese)
[5]魏文博,叶高峰,金胜,等.华北地区东部岩石圈导电性结构研究——减薄的华北岩石圈特点[J].地学前缘,2008,15(4):204-216.
WEI W B,YE G F,JIN SH,et al.Geoelectric structure of lithosphere beneath eastern North China:features of a thinned lithosphere from magnetotelluric soundings[J].Earth Science Frontiers(in Chinese),2008,15(4):204-216.(In Chinese)
[6]魏文博,金胜,叶高峰,等.藏南岩石圈导电性结构与流变性——超宽频带大地电磁测深研究结果[J].中国科学:D辑,2009(11):1591-1606.
WEI W B,JIN SH,YE G F,et al.Conductivity structure and rheological property of lithosphere in Southern Tibet inferred from super-broadband magnetotulleric sounding[J].Science in China(Series D:Earth Sciences),2009,39(11):1591-1606.(In Chinese)
[7]魏文博,金胜,叶高峰,等.中国大陆岩石圈导电性结构研究——大陆电磁参数“标准网”实验(SinoProbe-01)[J].地质学报,2010,84(006):788-800.
WEI W B,JIN SH,YE G F,et al.On the conductive structure of Chinese continental lithosphere-Experiment on"standard monitoring network"of continental EM parameters(SinoProbe-01)[J].Acta Geologica Sinica,2010,84(6):788-800.(In Chinese)
[8]WANNAMAKER P E.Anisotropy versus heterogeneity in continental solid earth electromagnetic studies:fundamental response characteristics and implications for physicochemical state[J].Surveys in Geophysics,2005,26(6):733-765.
[9]O'BRIEN D P,MORRISON H F.Electromagnetic fields in an n-layer anisotropic half-space[J].Geophysics,1967,32(4):668-677.
[10]REDDY I K,RANKIN D.Magnetotelluric Effect of Dipping ANISOTROPIES[J].Geophysical Prospec-ting,1971,19(1):84-97.
[11]PEK J,SANTOS F A M.Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media[J].Computers &geosciences,2002,28 (8):939-950.
[12]石应骏,刘国栋,吴广耀,等.大地电磁测深法教程[M].北京:地震出版社,1985.
SHI Y J,LIU G D,WU G Y,et al.A course in magnetotelluric method[M].Beijing:Seismology Publishing House,1985.(In Chinese)
[13]陈乐寿,王光锷.大地电磁测深法[M].北京:地质出版社,1990.
CHEN Y SH,WANG G Y.Magnetotelluric sounding method[M].Beijing:Geological Publishing House,1990.(In Chinese)
[14]林长佑,武玉霞,杨长福,等.水平层状对称各向异性介质的大地电磁资料反演[J].地球物理学报,1996,39:342-348.
LIN C Y,WU Y X,YANG C F,et al.Magnetotelluric inversion for symmetrically anisotropic layered medium[J].Geophys,1996,39:342-348.(In Chinese)
[15]阮爱国,李清河.EDA各向异性层状介质MT正演模拟[J].华南地震,1999,19(4):8-13.
RUAN A G,LI Q H.MT forward calculation in EDA anisotropy media[J].South China Journal of Seismology,1999,19(4):8-13.(In Chinese)
[16]霍光谱.二维大地电磁各向异性研究[D].北京:中国地质大学,2012.
HUO G P.Numerical modeling of magnetotelluric fields in two-dimensional anisotropic media[D].Beijing:China University of Geosciences,2012.(In Chinese)
[17]周建美.各向异性地层中可控源电磁法一维全参数反演及三维有限体积正演算法研究[D].长春:吉林大学,2014.
ZHOU J M.Studying on 1Dparameterized inversion and 3Dfinite volume simulation of controlled-source electromagnetic method in anisotropic formation[D].Changchun:JILIN University,2014.(In Chinese)
[18]霍光谱,胡祥云,刘敏.各向异性介质中大地电磁正演研究综述[J].地球物理学进展,2011,26(6):1976-1982.
HUO G P,HU X Y,LIU M.Review of the forward modeling of magnetotelluric in the anisotropy medium research[J].Progress in geophysics,2011,26 (6):1976-1982.(In Chinese)
[19]陈粲年,洪清泉,王建成.介质为各向异性的电磁场[M].北京:科学出版社,2012.
CHEN S N,HONG Q Q,WANG J C.Electromagnetic field for the anisotropic medium[M].Beijing:Science Press,2012.(In Chinese)
[20]李金铭.地电场与电法勘探[M].北京:地质出版社,2005.
LI J M.Geoelectric field and electrical prospecting [M].Beijing:Geological Publishing House,2005.(In Chinese)
[21]陈乐寿,刘任,王天生.大地电磁测深资料处理与解释[M].北京:石油工业出版社,1989.
CHEN Y S,LIU R,WANG T S.Magnetotelluric sounding data processing and interpretation[M].Beijing:Petroleum Industry Press,1989.(In Chinese)
[22]柳建新,童孝忠,郭荣文,等.大地电磁测深法勘探一资料处理、反演与解释科[M].北京:科学出版社,2012.
LIU J X,TONG X Z,GUO R W,et al.Magnetotelluric sounding exploration-data processing,inversion and interpretation[M].Beijing:Science Press,2012.(In Chinese)
Magnetotelluric forward research on horizontal layered electric anisotropic media
LIU Hong-zhoua,b,AN Ya-tinga,b
(China University of Geosciences a.Key Laboratory of Tectonics and Petroleum Resources of the Ministry of Education,b.Faculty of Earth Resources,Wuhan 430074,China)
The electrical anisotropic phenomena is universal in the earth interior.We theoretically derived tensor conductivity expressions for the electrical anisotropic media and formula of magnetotelluric forward modeling in layered electrical anisotropic media which was used for numerical calculating some geoelectric models and comparing with electric isotropic geoelectric model.It shows that the tensor electrical conductivity of anisotropic media is not only related with its inherent resistivity properties,but also measuring direction;The amplitude value of the apparent resistivity curve changes significantly when one of the electric anisotropy coefficient and the relative measurement angle changes,while the shape of the apparent resistivity curve basically remain unchanged;When the measuring direction is the same as electrical spindle orientation of electric anisotropic medium in the field of electromagnetic exploration,electric anisotropic medium model can be seen as two independent electric isotropic medium model.This study,hopefully,will contribute to the research and application of future electric anisotropic media magnetotelluric inversion.
tensor conductivity;magnetotelluric sounding;electrical anisotropy;forward research
P 631.3
A
10.3969/j.issn.1001-1749.2015.03.03
1001-1749(2015)03-0280-07
2014-07-13 改回日期:2014-10-08
国家自然科学基金项目(40702024);霍英东教育基金会项目(132020)
刘鸿洲(1990-),男,硕士,主要研究方向为电各向异性大地电磁测深法,E-mail:992414102@qq.com。
