基于地质统计先验信息的随机地震反演

叶端南，印兴耀，孙瑞莹，王保丽

（中国石油大学（华东）地球科学与技术学院，青岛 266580）

基于地质统计先验信息的随机地震反演

叶端南，印兴耀，孙瑞莹，王保丽

（中国石油大学（华东）地球科学与技术学院，青岛 266580）

基于地质统计先验信息的随机地震反演方法是一种基于蒙特卡洛的非线性反演方法。在贝叶斯理论框架下，通过序贯高斯模拟方法（sequential Gaussian simulation，SGS）和逐渐变形算法（Gradual Deformation Method，GDM）得到基于地质统计学的先验信息，然后构建似然函数，最终利用Metropolis算法实现后验概率密度的抽样，得到反演问题的解。与确定性反演结果相比，该方法能够有效地融合测井资料中的高频信息，提高反演结果的分辨率。数值模拟试验表明：本方法的反演结果与理论模型吻合较好，具有较高的分辨率；序贯高斯模拟采用一种新的逐点模拟方式，并结合GDM，有效提高了随机反演的计算效率。

地质统计先验信息；贝叶斯理论；高分辨率；计算效率

0 引言

石油勘探和开发已经从简单的构造识别转向复杂构造、薄储层以及老油区剩余油的研究。目前工业目标地质体的厚度一般在10m甚至10m以下，而实际的反演方法较难区分10m以下的薄层顶底［1］，所以提高分辨率以反演薄层信息在储层识别和油藏描述中起到了重要的作用。随着地球物理研究的深入，非线性反演方法更适用于复杂隐蔽性储层的研究。地球物理反演中普遍存在非线性和不适定性的问题，若采用线性方法来反演非线性反演问题通常较难得到其真值［2］，而随机反演能够在空间相关性和井的约束下，模拟出地震频带以外的信息，分辨率高于常规的确定性反演方法。因此，基于统计反演理论的非线性随机地震反演方法得到了进一步的发展［］。

Hass等［4］最早将地质统计学中的序贯高斯模拟技术与地震反演方法相结合，并以与实际地震数据的相似程度作为判别准则外推整个波阻抗数据体，这就是随机地震反演的雏形；Dubrule等人［5－6］进一步研究和发展了随机地震反演方法。序贯高斯模拟为经典的条件模拟方法，它是基于蒙特卡洛模拟思想发展起来的［7－8］，但是序贯高斯模拟方法的计算速度较慢。这里考虑采用Zou等人［9］提出的新的序贯高斯模拟实现方式，并结合Hu［10］提出的逐步变形更新算法（GDM）构建地质统计先验信息，以提高计算效率，从而实现随机地震反演。Kjønsberg等人［11］建议采用贝叶斯理论进行反演以获取后验概率密度的样本，这里假定基于地质统计学的先验信息和似然函数都服从高斯分布，那么得到的后验信息就服从非高斯分布，即不能得到后验概率密度的解析解。对于后验概率密度无法用公式表达的情况，需要对后验概率密度进行抽样来求解反问题。作者采用的抽样方法是Metropolis算法，基于蒙特卡洛的地震反演方法结合了Metropolis抽样算法、SGS算法和GDM扰动更新算法，可以为先验信息提供多参数扰动，从而加快收敛速度，提高反演精度。

1 方法原理

利用贝叶斯理论寻找反演问题的解，贝叶斯理论的一个优势就是在反演弹性参数的同时，可以得到不确定性的估计。基本思路就是在贝叶斯理论框架下，通过SGS算法得到高斯概率密度，再利用GDM扰动更新先验信息，然后根据地质统计先验信息和原始地震资料确定似然函数，最后利用Metropolis算法对后验概率密度进行抽样得到反演问题的解。图1为基于地质统计先验信息的随机地震反演流程图。

图1 基于地质统计先验信息的随机地震反演流程图Fig．1 Flowchart of stochastic seismic inversion based on the geostatistical priori information

1．1 贝叶斯理论

AVO反演的理论基础是Zoeppritz方程及其近似式。这里提出的随机地震反演方法在计算反射系数时，直接采用精确的Zoeppritz方程计算纵波反射系数，表示形式为：

其中：Rpp表示P波反射系数；Rps表示S波反射系数；Tpp表示P波透射系数；Tps表示S波透射系数；θ1和θ2分别为P波反射角和透射角；φ1和φ2分别为S波反射角和透射角；Δα、Δβ和Δρ分别表示界面两侧的纵、横波速度差及密度差，Δα＝（α2－α1），Δβ＝（β2－β1），Δρ＝（ρ2－ρ1）；α、β和ρ分别表示纵波速度、横波速度及密度；下标1和2分别表示界面上、下两侧的参数信息。

假设地震褶积模型为：

其中：d为观测地震数据；r为反射系数序列；G为子波褶积矩阵；e为噪音。根据贝叶斯理论可知［12］：

其中：ρM（R）表示储层弹性参数的先验信息；L（d／R）代表似然函数，表示模型与数据的匹配程度；σM（R）就是贝叶斯后验分布；k是概率归一化常数。这里直接采用精确的Knott-Zoeppritz方程计算正演合成地震记录，在一定程度上，可以减少Zoeppritz方程近似引起的误差。

1．2 地质统计先验信息

序贯高斯模拟（SGS）是常用的先验信息构建方法，但是SGS存在计算量较大的缺点，所以采用一种新的逐点模拟方式对测井数据进行序贯高斯模拟，为获得更多的模拟实现，结合GDM更新算法控制先验概率密度的微扰，而不是利用SGS重复模拟得到多个实现，这在一定程度上进一步提高了计算效率。因此可以结合SGS和GDM获得有效的先验信息，这就是所谓的基于地质统计学的先验信息。

1．2．1 SGS算法

序贯模拟的基本思想是沿随机模拟路径，将某一邻域内的所有已知数据（原始数据和先前已模拟的数据）作为条件数据进行模拟，获取每个网格节点的条件累积概率密度（CCDF），进而从CCDF得到模拟值。序贯高斯模拟适用于高斯模型，因此需确保原始数据服从高斯分布，若不服从，必须进行高斯变换，模拟结束后，进行高斯反变换。

以前的序贯高斯模拟是采用每次模拟整道数据或者逐点多次模拟的方式来匹配地震数据，这里使用Zou等人［9］提出的新的序贯高斯模拟实现方式，每次仅模拟一个点，并且每个网格只模拟一次，直至模拟完所有的网格节点，得到新的模型，该模拟方式在一定程度上可以提高反演结果的计算效率。

1．2．2 GDM更新算法

传统的随机反演方法在进行模拟时，即使达到了Metropolis抽样的接受条件，也不能保证模拟结果一定会使目标函数收敛，这里在利用新的SGS模拟方式提高计算效率的同时，引入了逐步变形更新算法，扰动更新SGS的实现，以保证模拟搜索时目标函数快速地收敛，从而达到提高反演精度的目的。

逐步变形算法最早由Hu等［13］提出，用来逐步修改高斯分布的储层模型，其后被扩展到非高斯分布储层的序贯指示模拟［14］。假设存在两个独立的高斯随机函数Z1和Z2，GDM算法可用于得到一个新的高斯场，即表示为两个独立的高斯随机函数的线性组合：

其中：p的取值范围为0～1／2；Z、Z1和Z2分别为更新的高斯白噪、当前待更新的高斯白噪和新加入的高斯白噪。由于高斯白噪Z的存在使得SGS算法具有随机性，不管模拟网格的大小，只需要对变形参数进行扰动就可以对整个模型进行修改，但由于没有改变协方差结构，所以这种扰动不会影响数据的空间变差结构。采用新的SGS模拟方式和GDM更新算法构建地质统计先验信息，可以有效地提高计算效率。

1．3 似然函数构建

对后验信息进行抽样时，接受概率的建立需要使用似然函数，似然函数采用如下形式：

其中：si代表模拟地震波形的振幅，是由弹性参数计算得到的合成记录；siobs是观测数据的采样点；σ是期望数据不确定性的标准差；Ri代表反演的弹性参数；Ri0是确定性反演中井位置处的低频约束（平滑约束和点约束）［15］；α是可调参数，当地震资料信噪比较高时，可选用较小的α值，当地震资料中含有多种噪音时，适当地增大α值。

1．4 Metropolis抽样

Metropolis抽样是一种基于蒙特卡洛的抽样方法［16］。需要对后验概率密度进行Metropolis抽样来得到反演问题的解。Metropolis准则表示为：

其中：mpropose是先验概率密度的信息；maccept是先前接受模型的扰动信息；Paccept是接受概率；其中的L就是似然函数。Gelman等人［17］发现，对高维分布来说接受概率应该约为23%，对于较大的接受概率，算法探索后验概率密度的速度过于缓慢。另一方面，对于较小的接受概率，计算试验量较大，所以应该调整各参数，例如变差函数的各种参数［18］、GDM扰动区域和GDM算法中p的取值等，使接受概率保持在23%左右。

在贝叶斯理论框架下，通过新的SGS方式得到高斯概率密度，然后利用GDM算法扰动更新模拟实现，就可以得到基于地质统计学的先验信息。根据确定性反演中井位置处的低频约束构建似然函数，最后利用Metropolis算法对后验概率密度进行抽样得到了反演问题的解。

2 模型试算

首先对如图2所示的一维数据进行试算分析，从反演结果可以看出，无论是反射系数、波阻抗还是合成地震记录，都和真实值比较匹配。

然后采用作者的反演方法对图3（a）所示的二维模型进行反演，该模型存在三个薄层，从中抽取10道数据作为伪井，如图3（b）所示，采用的子波是主频为30Hz、2ms采样的雷克子波，将模型的合成地震记录作为实际地震记录进行反演。图4为二维反演结果，其中（a）为随机道反演（反演的地震道数是随机的）的结果，（b）为逐道反演（按顺序，逐道进行反演）的结果，可以看出，利用这两种反演方式所得的结果和真实模型比较相似（似然函数中加入了较多的低频约束信息），并且能较好地识别薄层。利用基于地质统计先验信息的随机地震反演方法能够有效融合测井资料的高频信息，提高反演结果的分辨率，识别较薄的储层。

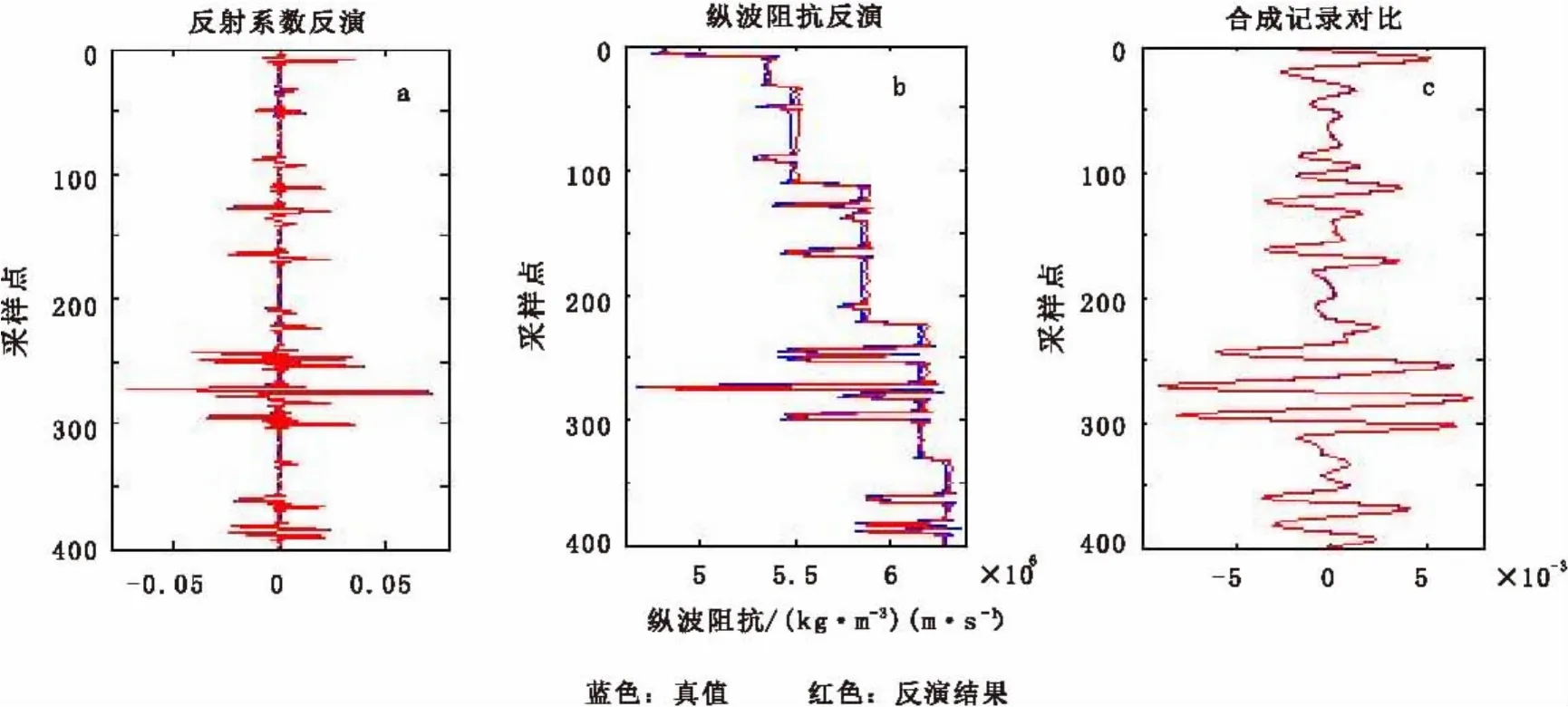
图2 单道反演结果对比Fig．2 Comparison of inversion results and real data

图3 原始数据Fig．3 The original data

3 实际资料测试

以国内某油田某区块的实际资料验证该方法的应用效果。图5是叠后地震数据，图6是稀疏脉冲反演与随机反演的对比，其中图6（a）是稀疏脉冲反演结果，图6（b）是随机地震反演结果，黄色为含油砂岩（对应较高阻抗），蓝色为泥岩和含水砂岩（对应较低阻抗）。从图6中可以明显地看出，随机反演结果的分辨率高于稀疏脉冲反演。稀疏脉冲反演最多可识别7m左右的储层，仅比地震数据的分辨率高一些，随机反演可以识别3m左右的储层，反演精度比较高。如图6中黑色椭圆中所示，井A上有一个6．6 m的油层，是一个薄互层（由两个薄油层构成），利用稀疏脉冲反演方法不能分辨，而随机反演可以将两者区分开来。井B黑色圆圈内上方有一个3m左右的薄油层，稀疏脉冲反演没有反演出来，而随机反演却分辨出了该薄层。因此通过实际资料分析可以得到，随机反演的分辨率高于稀疏脉冲反演，这里并不是说随机反演方法优于确定性反演，而是两者各有其适用性，需要根据具体问题具体分析，因为确定性

反演速度较快，当反演较厚的储层时，可以应用稀疏脉冲反演；而当实际工区需要进行薄层的识别时需要应用随机地震反演方法。

图4 随机地震反演结果Fig．4 Stochastic seismic inversion results

图5 叠后地震剖面Fig．5 The post－stack seismic profile

4 结论与认识

序贯高斯模拟是经典的地质统计学模拟方法，而GDM更新算法能够连续更新储层参数实现使目标函数快速收敛，并且随机地震反演能够有效融合测井的高频信息，提高反演结果的分辨率，但计算效率是其面临的一个问题。结合序贯高斯模拟和GDM更新算法进行随机反演，新的模拟方式结合GDM有效提高了计算效率，并且通过模型试算和实际资料分析结果表明，该反演方法能够稳定地收敛，反演结果比较可靠。

需要强调的是，基于地质统计先验信息的随机地震反演方法中，变差函数的影响非常重要，特别是二维和三维的反演过程中，各向异性变差函数对反演结果的影响会很明显，可考虑通过各向异性变差函数改善随机反演的横向连续性。

图6 稀疏脉冲反演与随机反演的对比Fig．6 Comparison of CSSI and SI

［1］CHOPRA S，CASTAGNA J，PORTNIAGUINE O．Seismic resolution and thin－bed reflectivityinversion［J］．CSEG recorder，2006，31（1）：19－25．

［2］ASTER R C，BORCHERS B，THURBER C H．Parameter estimation and inverse problems［M］．Academic Press，2013．

［3］FRANCIS A．Limitations of deterministic and advantages of stochastic seismic inversion［J］．CSEG Recorder，2005，30：5－11．

［4］HAAS A，DUBRULE O．Geostatical inversion－a sequential method of stochastic reservoir modelling constrined by seismic data［J］．First break，1994，13（12）：561－569．

［5］DUBRULE O，THIBAUT M，LAMY P，et al．Geostatistical reservoir characterization constrained by 3Dseismic data［J］．Petroleum Geoscience，1998，4（2）：121－128．

［6］ROTHMAN D H．Geostatistical inversion of 3D seismic data for thin－sand delineation［J］．Geophysics，1998，51（2）：332－346．

［7］印兴耀，贺维胜，黄旭日．贝叶斯－序贯高斯模拟方法［J］．石油大学学报：自然科学版，2006，29（5）：28 －32．

YIN X Y，HE W S，HUANG X R．Bayesian sequential Gaussian simulation method［J］．Journal of the University of Petroleum，2006，29（5）：28－32．（In Chinese）

［8］印兴耀，刘永社．储层建模申地质统计学整地震数据的方法及砰究进展［J］．石油地球物理勘探，2002，37（4）：423－430．

YIN X Y，LIU Y S．Methods and development of integrating seismic data in reservoir model－building［J］．OGP，2002，37（4）：423－430．（In Chinese）

［9］ZOU Y M，LIU W L，ZHOU H，et al．A new implementation procedure of sequential Gaussian simulation in stochastic seismic inversion［C］／／2013 SEG Annual Meeting，2013．

［10］HU L Y．Gradual deformation and iterative calibration of Gaussian－related stochastic models［J］．Mathematical Geology，2000，32（1）：87－108．

［11］KJØNSBERG H，HAUGE R，KOLBJØRNSEN O，et al．Bayesian Monte Carlo method for seismic predrill prospect assessment［J］．Geophysics，2010，75（2）：09－019．

［12］JOHN A，SCALES，MARTIN L．SMITH，SVEN TREITEL．Introductory Geophysical Inverse Theory ［M］．Golden：Samizdat Press，2001．

［13］HU L Y，BLANC G．Constraining a reservoir facies model to dynamic data using agradual deformation method［C］．6th European Conference on the Mathematics of Oil Recovery．1998．

［14］HU L Y，LE RAVALEC M，BLANC G，et al． Reducing uncertainties in production forecasts by constraining geological modeling to dynamic data［C］．SPE Annual Technical Conference and Exhibition．Society of Petroleum Engineers，1999．

［15］杨培杰．地震子波盲提取与非线性反演［D］．东营：中国石油大学（华东），2008．

YANG P J．SeismicWavelet Blind Extraction and Non －Linear Inversion［D］．Dongying：China University of Petroleum（Huadong），2008．（In Chinese）

［16］MOSEGAARD K，TARANTOLA A．Monte Carlo sampling of solutions to inverse problems［J］．Journal of Geophysical Research：Solid Earth（1978–2012），1995，100（B7）：12431－12447．

［17］GELMAN A，ROBERTS G，GILKS W．Efficient metropolis jumping hules［J］．Bayesian statistics，1996，5：599－608．

［18］ZHANG G Z，LIU Y S，YIN X Y．The Effects of Factors of Spatial Correlation Analysis On Kriging Estimate In Geostatistical Reservoir Characterization［C］．2005SEG Annual Meeting．Society of Exploration Geophysicists，2005，1457－1460．

Stochastic seismic inversion based on the geostatistical priori information

YE Duan-nan，YIN Xing－yao，SUN Rui-ying，WANG Bao-li
（School of Geosciences，China University of Petroleum，Qingdao 266580，China）

Stochastic seismic inversion based on the geostatistical priori information is a Monte Carlo based strategy for non －linear inversion．It is formulated in a Bayesian framework．Firstly，the priori information can be obtained through sequential Gaussian simulation（SGS）and gradual deformation method（GDM）．Then we can construct the likelihood function．Finally，we apply Metropolis sampling algorithm in order to obtain an exhaustive description of the posteriori probability density and get the inversion results．Compared with the deterministic inversion，the inversion method we proposed can effectively integrate the high－frequency information of well－logging data and have a higher resolution．According to the numerical calculations，the final results match the model well and have a high resolution．In addition，we use the sequential Gaussian simulation（SGS）in a new implementation way and combine with GDM，which can improve the calculation efficiency of inversion method effectively．

geostatistical priori information；Bayesian theory；high-resolution；calculation efficiency

P 631．4

A

10．3969／j．issn．1001-1749．2015．03．12

1001-1749（2015）03-0341-07

2014-02-25 改回日期：2014-07-01

国家973项目（2013CB228604）；国家科技重大专项（2011ZX05009）；山东省自然科学基金（ZR2011DQ013）；国家自然科学基金（41204085）；中国石化地球物理重点实验室（WTYJY－WX2013－04－07）

叶端南（1984－），男，博士，主要研究方向为地震储层预测，E-mail：yedn＠upc．edu．cn。