西藏甲玛铜多金属矿床储量的协同克立格估值

蒋 鑫，庹先国，，柳炳琦，李怀良

（1．成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059；2．西南科技大学核废物与环境安全国防重点学科实验室，绵阳621010）

西藏甲玛铜多金属矿床储量的协同克立格估值

蒋 鑫1，庹先国1，2，柳炳琦1，李怀良2

（1．成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059；2．西南科技大学核废物与环境安全国防重点学科实验室，绵阳621010）

西藏甲玛铜多金属矿矿区元素分布复杂，传统的地质统计学方法对其进行储量估算时忽略了多金属的相互影响，因此为了反映出不同金属元素的空间变异情况，采用协同克里格法对该矿区的金属元素储量进行估算。这里首先介绍了协同克里格算法的相关理论和相关技术，然后以此为基础，对不同方向上的空间变差函数进行结构套合的优化，并对协同克里格方程组进行降维处理。最后以2012年甲玛矿区勘探工程的数据为例，以Cu为主区域化变量，以Ag为协同区域化变量，计算了各自的实验变差函数和交差实验变差函数，分别进行协同克里格法插值和普通克里格法插值。交叉验证结果表明，协同克里格估值的标准差为0．6477，在储量计算上面精度更高，并能广泛应用于西藏甲玛铜多金属矿的地质属性、储量估算等空间数据建模。

储量估算；协同克里格；空间变异；结构套合

0 引言

西藏墨竹工卡县甲玛夕卡岩－角岩型铜多金属矿床是目前我国同类矿床矿石品质最好、成矿元素多，探明的资源量已经达到超大型规模的矿床［1］。目前对于该地区的储量估算已经采用的是传统断面法［4］、SD法［2］和地质统计学方法［3］，其中地质统计学方法不但能给出结果的估算精度而且是无偏且估计方差最优的，这些优势恰好是传统方法所缺少

的［5］。

西藏甲玛铜多金属矿的区域内地层比较复杂，地层曲面变化比较大，甚至可能存在地层曲面相交和错断的情况，并且多种金属之间会出现协同区域化［11－14］的现象，即多种金属的储量分布会相互影响。在这样一种情况下，就需要我们解决如何寻找一种合适的方法消除多金属相关关系的影响。这里采用协同克里格法对该矿区的空间变异进行分析，并且对矿区的铜元素储量估算进行实例验证。验证结果发现，协同克里格法的估算结果更符合实际情况，对深化矿业和石油行业开发地质随机建模理论和有效开采剩余矿产石油资源，具有重要的理论意义和现实意义。

1 协同克里格算法原理

在西藏甲玛铜多金属矿的观测数据中，常遇到多个变量协同区域化的现象，如银、铜、铅、锌等几个变量的协同区域化，当某一个变量的取样量不足以获得所需精度的估计量，而其他变量却有较充足的取样量时，研究这个变量与其他变量间的空间相关关系，借助其他变量的样品信息用协同克里格法就可以提高对这个变量的估计精度。设有K个二阶平稳的变量构成协同区域化变量｛Zk（x），k＝1，2，…，K｝，其数学期望为：

设k0为k＝1、2、…、K中某一特定值，即设Zk0（x）为我们要估计的主变量，设要估计的是中心点在x0处的承载Vk0（x0）上Zk0（x）的平均值：

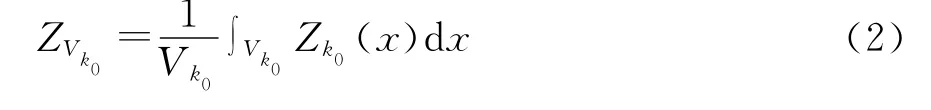
有效数据集是｛Zak，ak＝1，2，…，nk｝，k＝1、2、…、K，而Zak是确定在承载Vak上的平均值，即：

要得到待估样本点的无偏最优估计值，必须满足最小方差无偏估计的要求：

为使估计方差达到最小，则要求权重系数要满足协同克立格方程组，即：

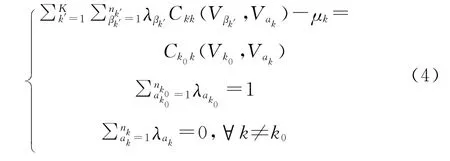
其中：∀ak＝1、2、…、nk；k＝1、2、…、K，这个方程组的未知数是个权系数λak及K个拉格朗日参数μk；共有＋K个未知数，同时也有＋K个线性方程构成这个方程组。

2 协同克里格算法的改进与实现

2．1 交叉变差函数的建立

如式（1）所示的二阶平稳的协同区域化变量，其互协方差函数即交叉变差函数的定义为：

对交叉变差函数和变差函数进行离散计算时，需要用球状模型拟合理论变差函数。球状函数模型的一般公式为：

其中：C0为块金效应，它表示h很小时两个样品点之间品位的变化；a为变程，当h＞a时，任意两样品点就不在具有相关性。以球状函数为基础，通过计算可以得出交叉变差函数的理论模型。

2．2 求解协同克里格方程组

将式（4）转化成矩阵形式为：

普通克里格方程组只要在二阶平稳条件下，总是可以用协方差函数表示，又可以用变差函数表示。而协同克里格方程组不同，二阶平稳条件下，只有当Ck′k（h）＝Ckk＇（h），从而λk′k（h）＝Ck′k（0）－Ck′k（h）成立时，才可用交叉协方差函数表示。

2．3 优化协同克里格方程组

这里主要从两个方面来优化［6－10］协同克立格算法，①变差函数；②从求解协同克立格方程组。因为在实际问题中，各个方向的变差函数是不一样的，就需要研究不同方向上的结构套合问题，主要是通过计算不同方向的变差函数值后，再用球状模型来拟合实验变差函数，最后进行结构套合。改进后变差函数流程图如图1所示。

在求解协同克立格方程组系数时，协同克立格方程组的维数与样品数据个数有直接关系，也就是说样品数据越多，方程组维数越大。这就需要对协同克立格方程组进行降维处理或者减少协同克立格方程组的数目，协同克立格方程组的矩阵形式为式（8）。

针对研究数据样本，样本数据构形相同，协同克立格矩阵［K］相同，所以只需计算一次［K］－1，假设每次估值计算时，待估块段大小相等，几何特性相等，那么［M］（M表示协方差函数向量）相同。这时，就只需要求解一次协同克立格方程组，所得到的权重系数［λ］＝［K］－1［M］，就适合所有的待估块，就能进行比较快速的计算。权值校正的协同克里格算法流程如图2所示。

图1 变差函数流程图Fig．1 Flow chart of variogram

图2 协同克立格插值算法流程图Fig．2 Flow chart of Cokriging

图3 地表及钻孔点三维模型图Fig．3 3Dmodel diagram of surface and drill

3 应用实例

作者以西藏自治区墨竹工卡县甲码铜多金属矿床储量估算为例。原始数据为截止2012年甲玛矿区勘探工程的数据。包括58个钻孔，共计15 187件化学样。每个钻孔均有完整的测斜数据共568个。矿床地表模型及钻孔点的三维模型如图3所示。

3．1 数据预处理

对矿床储量的协同克里格法估值，首先需要对钻孔数据进行特异值处理与样品组合处理，以Cu元素的计算进行实例说明。首先根据Cu的品位数据，在正态概率纸上作累积频率曲线图（图4）。

图4表明Cu品位的累积频率符合正态分布，并且存在少量异常偏大的离散点，我们才认为它们是真正的特异值。对这种异常的特高品位点用上截品位代替，取第一个发生偏离的品位值为上截品位，将所有高于上截品位的品位数据全部用上截品位值代替。代替前、后的统计分析见表1。原始数据样品长度各不相同，需要进行样品组合，组合后的Cu元素特征值的统计结果见表2。

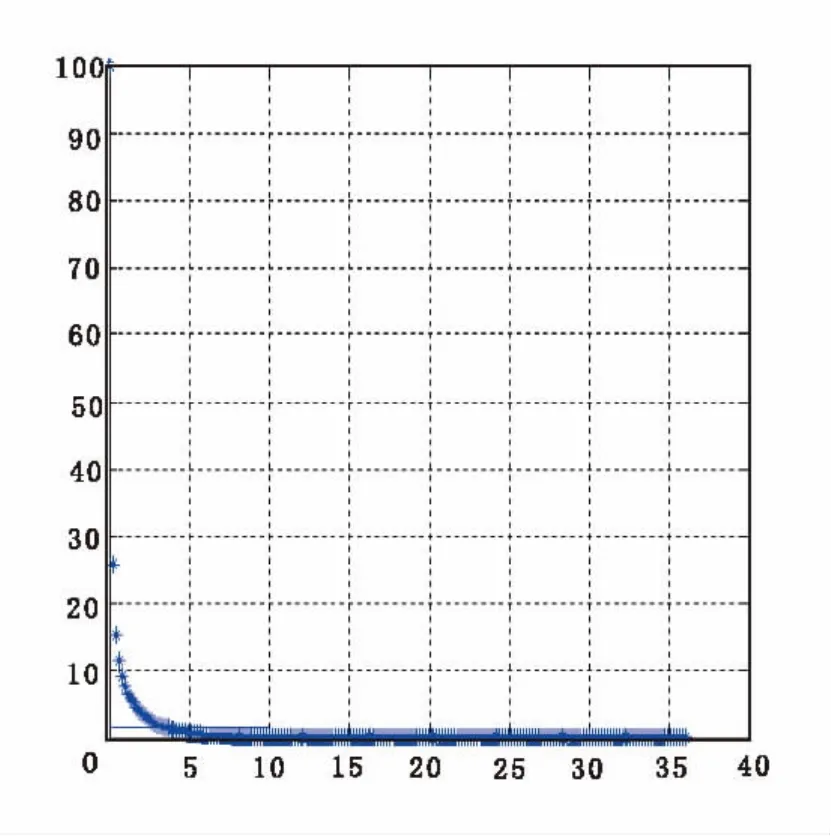
图4 Cu元素累积频率曲线图Fig．4 Cumulative frequency curves of Cu

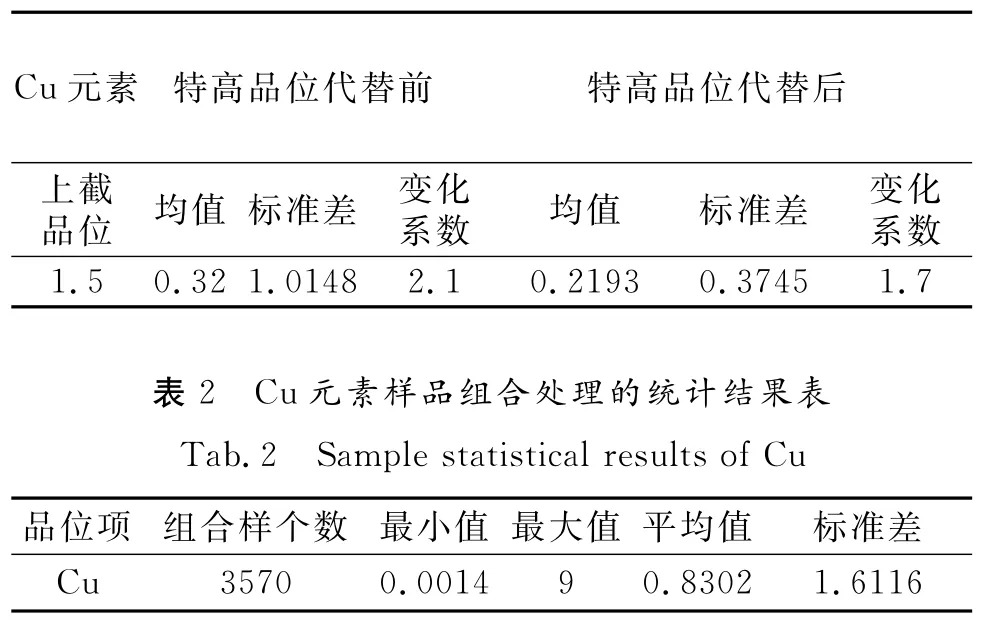
表1 Cu元素特异值处理结果Tab．1 The results of specific values of Cu

3．2 协同克里格法估算储量

3．2．1 变差函数及结构分析

对组合样本进行统计分析，分析结果如表3所示，组合样品中Cu的品位数据与Ag的品位数据相关程度最大，所以以Ag元素作为辅助变量对Cu元素的品位进行估值。

进行协同克里格法插值的第一步是得到Cu品位和Ag品位的变差函数，以及两者的交叉变差函数。把所有钻孔点两两组合成点对，计算出其距离值，再以球状模型拟合成理论实验变差函数。Cu品位项和Ag品位项的三个变差函数轴的方向定位及其计算结果见表4。

表3 组合样本统计分析表Tab．3 Combined sample analysis table

表4 Cu和Ag元素变差函数参数表Tab．4 Variogram Parameter of Cu and Ag

图5 变差函数图Fig．5 Diagram of variogram

两种元素品位的变差函数图见图5。

从图5可以看出，两种元素在各个方向上的变差函数比较相似，因此所有变差函数都是各向同性的。对Cu品位项和Ag品位项的三个轴方向上的变差函数进行结构套和，套和结果如下：

Cu品位的变差函数模型为：

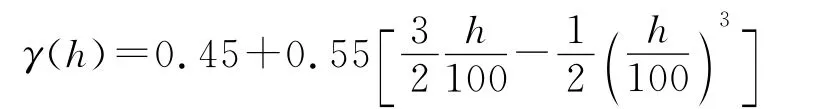
Ag品位的变差函数模型为：

以这两种品位为基础计算它们的交叉变差函数，同样交叉变差函数的变化趋势满足球状模型，所以用球状模型拟合计算出交叉变差函数的基台值为0．58，拱高为0．42，变程为55m，其变差函数图如图6所示。

图6 交叉变差函数图Fig．6 Diagram of interactive variogram

3．2．2 算法模型验证

为了检验协同克里格插值的合理性，采用交叉验证方法对钻孔点依次求解。其基本原理是从信息样集合中临时抽取一个点作为已知值，利用协同克里格插值模型去估算这个已知值，然后对计算结果和真实值的差值进行统计分析。以Cu元素的品位估值情况进行交叉验证为例，验证结果见图7。

同理用普通克里格插值模型和已知样品去估算已知值，与协同克里格模型相比结果见表5。

表5 协同克里格验证结果表Tab．5 Result of Cokriging

从图7可以看出，Cu元素品位的残差值大部分在3以内，与实际钻孔值相当接近，表明模型确定合理，能用于下一步的储量计算。与普通克里格模型相比发现，在3 570个组合样品点上，协同克里格插值模型减少了估值的平均误差，并且普通克里格插值模型的标准差总是高于协同克里格插值模型的标准差，这表明协同克里格模型在储量计算上面精度更高。

3．2．3 储量计算

针对三维块段模型的储量计算，运用变差函数的特征确定单元块段的尺寸参数（表6）。

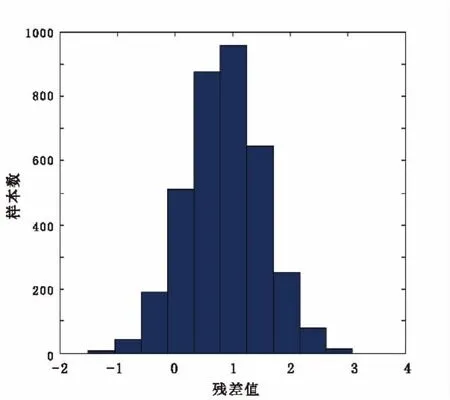
图7 交叉验证结果图Fig．7 Result of interactive verification

表6 块段估值参数表Tab．6 Valuation parameter block segment table

由表6可以看出，甲玛矿区总共划分出153 600个单元块段，对每个单元块段的Cu品位进行估值时，需要确定对于该估值点的搜索范围。由于Cu品位的变差函数模型以及与辅助变量之间的交叉变差函数模型都呈球状模型变化趋势，而球状模型的特点是变差函数值随着距离变化到变程时，变差函数值就稳定为基台值，所以变程大小直接影响待估单元块段的搜索区域。进行协同克里格估值时，搜索范围定义为具有一个长轴和两个短轴的三维椭球体，综合Cu品位球状模型参数和矿区钻孔分布间隔的因素，搜索的三维椭球体设长轴为200m，次轴为200m，短轴为30m，在整个椭球体内部的单元块段都要参与估值计算（图8）。

通过计算，2012年西藏甲玛矿区的勘探区域共探获铜金属量为229×104T（只考虑银元素为辅助变量）。

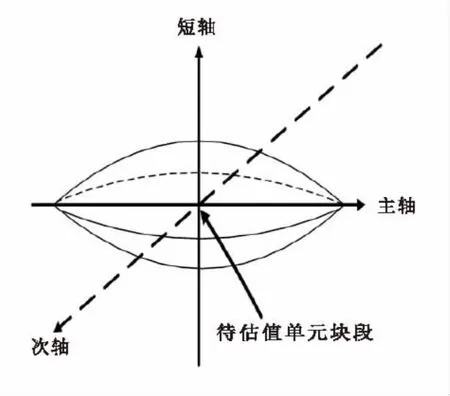
图8 搜索范围图Fig．8 Diagram of search field

4 结语

对于西藏自治区墨竹工卡县甲码铜多金属矿床储量估算，当用传统普通克里格方法进行插值计算时，没有考虑不同金属元素的相关关系，插值精度不高。基于此，作者采用协同克里格法，并对协同克里格法进行优化，能快速地计算西藏甲码铜多金属矿的资源储量。作者首先对钻孔数据资料进行了统计分析和预处理，然后计算Cu元素和Ag元素的变差函数及其交叉变差函数以构造协同克里格方程组，通过求解方程组得出权值系数。最后对甲玛矿区的Cu元素储量进行了估算，得到Cu金属量为229× 104T。同时通过方差验证，与普通克里格法的验证结果进行对比，结果发现，协同克里格法因为反映了不同金属元素品位间的空间变异情况，可靠性更高，能为矿山开采设计提供科学、可靠的依据。

［1］黎枫佶．西藏墨竹工卡县甲玛铜多金属矿三维模型构建和资源量估算［D］．成都：成都理工大学，2010．

LI F J．Constructing 3Dmodels and estimating reserves of Jiama polymetallic copper deposit，MoZhugongka county，Tibet［D］．Chengdu：Chengdu University of Technology，2010．（In Chinese）

［2］柳炳利．基于SD法的固体矿产资源研究［D］．成都：成都理工大学，2009．

LIU B L．Research of solid mineral resources based on the SD method［D］．Chengdu：Chengdu University of Technology，2009．（In Chinese）

［3］程勖．地质统计学软件开发与应用［D］．长春：吉林大学，2009．

CHENG X．Geostatisties sottware development and application［D］．Changchun：Jilin University，2009．（In Chinese）

［4］施俊法，唐金荣，周平，等．世界找矿模型与矿产勘查［M］．北京：地质出版社，2010．

SHI J F，TANG J R，ZHOU P，et al．The world model of prospecting and exploration of mineral resources［M］．Beijing：geological publishing house，2010．（In Chinese）

［5］杨学善，秦德先，邓明国．地学空间数据库建设快捷方法研究［J］．煤田地质与勘探，2005，33（5）：16－19．

YANG X SH，QIN D X，DENG M G．Shortcut methods of spatial database constru－ction for geosciences［J］．Coal Geology ＆Exploration，2005，33（5）：16－19．（In Chinese）

［6］李庆谋．多维分形克里格方法［J］．地球科学进展，2005，20（2）：248－256．

LI Q M．Multi－fractal Krige interpolation method［J］．Advances in Earth Science，2005，20（2）：248－256．（In Chinese）

［7］肖克炎，张晓华，王全明，等．应用改进的克里格法分离重力区域异常与局部异常［J］．物探化探计算技术，1995，17（2）：19－25．

XIAO K Y，ZHANG X H，WANG Q M，et al．Separation of regional field and local field by improved Kriging method［J］．Computing Techniques for Geophysical and Geochemical Exploration，1995，17（2）：19－25．（In Chinese）

［8］高美娟，朱庆忠，张淑华．利用贝叶斯－克里金估计技术进行储层参数预测［J］．石油地球物理勘探，1999，34（4）：390－397．

GAO M J，ZHU Q ZH，ZHANG SH H．Reservoir parameter prediction using Bayes－Kriging estimation technique［J］．OGP，1999，34（4）：390－397．（In Chinese）

［9］汪保，孙秦．改进的Kriging模型的可靠度计算［J］．计算机仿真，2011，28（2）：113－116．

WANG B，SUN Q．Structural reliability computation based on Kriging model［J］．Computer Simulation，2011，28（2）：113－116．（In Chinese）

［10］牛文杰，孟宪海，李吉刚．结合软数据的同位置协同克里金估值新方法［J］．煤田地质与勘探，2011，39（2）：13－17．

NIU W J，MENG X H，LI J G．A new estimation method of collocated CoKing combined with soft data［J］．Coal Geology ＆Exploration，2011，39（2）：13－17．（In Chinese）

［11］孙红泉．地质统计学及其应用［M］．北京：中国矿业大学出版社，1990．

SUN H Q．Geostatistics and its application［M］．Beijing：China University of Mining Press，1990．（In Chinese）

［12］侯景儒，黄竞先．地质统计学的理论与方法［M］．北京：地质出版社，1990．

HOU J R，HUANG J X．The theory and method of Geostatistics［M］．Beijing：geological publishing house，1990．（In Chinese）

［13］孙仁铎．空间变异理论及其应用［M］．北京：科学出版社，2005．

SUN R D．the Spatial Variability Theory and Application［M］．Beijing：Science Press，2005．（In Chinese）

［14］孙红泉，康永尚，杜惠芝．实用地质统计学程序集［M］．北京：地质出版社，1997．

SUN H Q，KANG Y SH，DU H ZH．The utility of geostatistical procedures set［M］．Beijin：geological publishing house，1997．（In Chinese）

Estimation of reserves based on Cokriging in Jiama polymetallic copper deposit，Tibet

JIANG Xin1，TUO Xian-guo1，2，LIU Bing－qi1，LI Huai-liang2
（1．State Key Laboratory of Geohazard Prevention and Geoenvironment Protection，Chengdu University of Technology，Chengdu 610059，China；2．Key Laboratory for Radioactive Waste and Environmental Security，Southwest University of Science and Technology，Mianyang 621010，China）

The distribution of mining area element is very complex in Jiama polymetallic copper deposit，Tibet．Traditional geostatistical method ignored the phenomenon of mutual influence more metal on the reserves estimation．In order to reflect different metal elements of space mutation，metal reserves of the mine area is estimated based on the cokriging method in this paper．The paper first introduces the relevant theory and technology of the Cokriging algorithm，then optimizes spatial variation function in different directions to structure of nested，and decreases the dimension of cokriging equations．Finally，by taking an example of the data of exploration engineering for Jiama mining area in 2012，with Cu as the main regionalized variables and with Ag as collaborative regionalized variables，this paper calculate the experimental variogram and the interactive experimental variogram，respectively，Cokriging interpolation and the ordinary kriging interpolation．Cross validation results point out that the standard deviation of Cokriging is 0．6477，and the Cokriging is higher in the calculation of reserves above precision．The Cokriging can be widely used in the geological properties，reserve estimation and spatial data modeling of Jiama polymetallic copper deposit，Tibet．

estimating reserves；Cokriging；spatial variation；structure of nested

P 632

A

10．3969／j．issn．1001-1749．2015．03．16

1001-1749（2015）03-0372-07

2014-07-01 改回日期：2014-08-13

国家自然科学基金重大科研仪器设备研制专项（41227802）；国家杰出青年基金（41025015）

蒋鑫（1991－），男，硕士，研究方向为计算机应用，现主要从事勘探设备软件开发，E-mail：jiangxin＿cdut＠163．com。