螺旋叉指电极式压电圆片换能器的有限元分析与实验比较
2015-05-25肖广军潘成亮刘永斌潘巧生
肖广军,潘成亮,刘永斌,3,潘巧生
(1.中国科学技术大学工程科学学院,合肥230026;2.合肥工业大学仪器科学与光电工程学院,合肥230009; 3.安徽大学电气工程与自动化学院,合肥230039)
螺旋叉指电极式压电圆片换能器的有限元分析与实验比较
肖广军1,潘成亮2,刘永斌1,3,潘巧生1
(1.中国科学技术大学工程科学学院,合肥230026;2.合肥工业大学仪器科学与光电工程学院,合肥230009; 3.安徽大学电气工程与自动化学院,合肥230039)
螺旋叉指电极式压电圆片换能器可以产生面内扭转运动,具有结构简单、加工方便、性能可靠等优点,可用于超声马达、光学扫描、黏度测量等领域;但表面螺旋叉指电极间陶瓷材料的极化方向变化复杂,给换能器的机电耦合分析和优化设计带来极大的难度。利用坐标变换思想与有限元方法,将压电圆片分割成若干子体,通过极化电场分析确定子体局部坐标系以定义材料参数,从而实现复杂极化情况下压电换能器的耦合仿真分析。利用ANSYS有限元软件,优化仿真分析过程,研究了该压电圆片换能器的静态扭转位移径向分布特性和动态导纳频率响应特性,并与实验结果相比较,证实了该方法的可行性和有效性。
压电陶瓷;圆片换能器;螺旋叉指电极;面内扭转;有限元仿真
作为一种机电耦合器件,压电换能器通过压电效应或逆压电效应,可以实现机械能和电能的互相转化,其在精密传感器和先进驱动器领域获得了广泛应用,如超声马达、压电泵、光学扫描器、黏度计和能量回收装置等[1-2]。近年来,随着压电换能器的发展,学者们相继提出一系列新型换能器结构,如超螺旋结构[3]和螺旋纤维管[4]等,这类换能器复杂的结构设计和非一致的极化电场分布,使精确的理论分析变得非常困难,很难为换能器的结构分析和优化设计提供有效参考。因此,人们常借助于有限元分析等方法解决复杂结构的压电耦合分析问题。
本课题组提出了一种基于螺旋叉指电极的面内扭转压电圆片换能器[5],具有结构简单、加工方便、性能可靠等优点。在该换能器的分析过程中,由于表面叉指电极形成的复杂电场分布,导致了极化后的材料参数分布复杂,使得简化的理论分析与实验结果之间存在较大的差异。另一方面,有限元法作为一种可行的机电耦合特性仿真分析途径,目前处理的压电换能器通常具有均匀一致的极化电场[6-7],但螺旋叉指电极式压电换能器的极化电场方向始终垂直于螺旋电极线,在总体笛卡尔坐标系下该方向随着电极线变化,导致材料参数的定义亦发生变化。因此,如何给压电单元准确定义极化方向和材料参数是有限元仿真分析过程中的主要难点,建立复杂极化条件下的有限元分析模型将会有力地促进人们对这类新型压电换能器的理解和发展。
法国学者提出一种基于坐标变换思想的有限元方法用于压电纤维扭转驱动器的仿真分析[8],但文章侧重于仿真结果的分析,对该方法本身的分析步骤优化和仿真内容扩展未有深入研究。本文开展上述螺旋叉指电极式压电圆片换能器的有限元分析研究,优化分析步骤,通过静态、模态、谐响应等仿真分析内容,研究该换能器扭转位移径向分布特性和导纳频率响应特性,并对加工样品进行实验测试,比较验证该有限元法的可行性和有效性。
1 压电圆片换能器有限元模型
螺旋叉指电极结构是表面叉指电极的一种特殊形式,n对特殊设计的螺旋电极线通过内外两个联结电极环分别形成换能器的正极和负极(见图1)。定义螺旋线的切线方向与过该点的圆周切线之间的夹角α为螺旋角,两条螺旋线之间的垂直距离为Δd。螺旋电极的曲线形状并不唯一,有两种基本的形式:等螺旋角和等间距螺旋电极。本文的主要研究等间距螺旋电极的压电换能器,在极坐标系下,等间距螺旋线可通过下式定义

图1 螺旋叉指电极式压电圆片换能器示意图Fig.1 Schematic of the discal piezoelectric transducer with spiral interdigitated electrodes
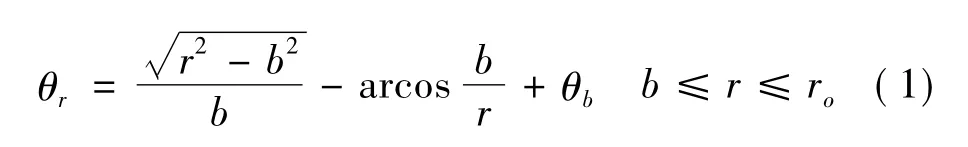
式中:b是螺旋角为90°时的半径。对于等间距螺旋线,不同半径处的螺旋角α是变化的,但始终满足r sinα= b。压电陶瓷圆片的外圈直径为d,厚度为t,螺旋线的端部对应的半径分别为ri和ro,ri和ro之间的区域为有效极化和驱动范围,中间的圆形为非极化区域。在应用中,换能器的外边缘面固定,产生面内扭转运动用于驱动或传感。
通常,压电换能器的机电耦合关系用123极化坐标系下的压电方程描述,其D型方程可表示为
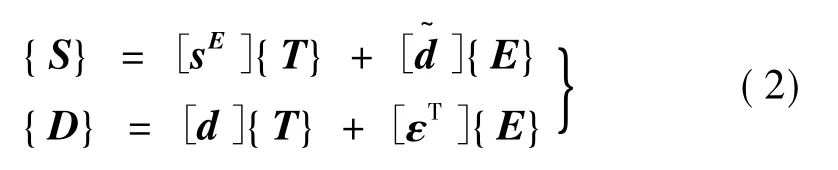
式中:S和T分别为应变和应力矩阵,E和D分别为电场和电位移矢量矩阵,d为压电系数矩阵,sE为恒电场条件下的弹性柔顺系数矩阵,εT为应力条件下的介电常数矩阵。
利用坐标变换思想,将换能器整体划分为若干子体,假定每个子体内的陶瓷材料极化特性一致,不同子体分别定义极化方向和材料参数,从而完成后续有限元分析过程。在有效极化区域,123局部极化坐标系可由xyz总体笛卡尔坐标系旋转得到,则应力、应变、电场和电位移在两个坐标系下的矩阵变换关系可表示为

式中:T'、S'、E'和D'分别为总体坐标系下的对应矩阵; A、B和C分别为相应坐标变换矩阵,与各个子体两个坐标系的相对位置有关,可由邦德矩阵变换法则求得[9]。将式(3)代入式(2),可得到总体笛卡尔坐标系下的压电方程,如下所示
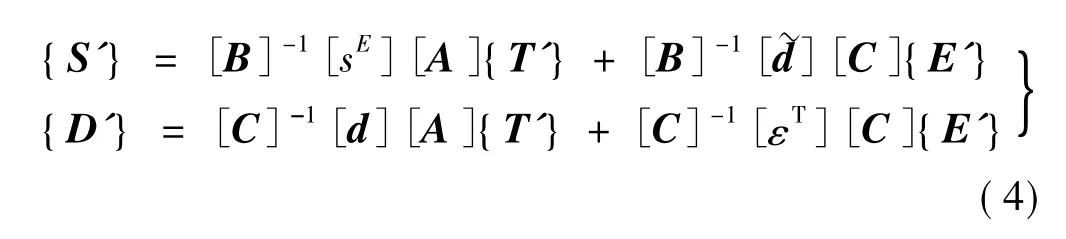
有限元法以变分原理和剖分插值为基础,将连续体离散成有限单元,建立有限元离散化方程并结合载荷、初始、边界等条件求解,限于篇幅,本文对有限元离散化方程的推导过程不再赘述,详细内容可参考文献[9]。
2 ANSYS有限元仿真分析步骤与方法优化
2.1 分析步骤
针对复杂极化条件下的压电耦合仿真分析,我们利用坐标变换的思想,通过将压电单元整体分割成若干子体的方法来解决这类问题。螺旋叉指电极式压电圆片换能器的极化方向受电极螺旋角影响而变化,因此ANSYS仿真的难点在于如何准确地定义各子体压电材料的极化方向。依据螺旋电极的结构形式,合理地把圆片换能器规划分割成合适数量的子体,当分割的子体足够多时,就可以认为每个子体内压电陶瓷的材料性质是一致的。此时,换能器整体的极化方向定义就变成了给每个子体定义极化方向,并以此赋予各个子体准确的材料参数。
换能器的压电耦合分析过程如下:①根据电极的结构特点,建立几何模型,划分初级网格,进行静电场分析,获得极化电场分布结果;②通过get函数获取初级网格单元节点的位置坐标和极化电场信息建立数据库,用于二次参数建模;③通过循环函数,利用初级网格单元节点位置坐标信息将初级网格单元转换为子体;④利用初级网格单元节点极化电场信息,取子体对应节点极化电场平均值,获得子体近似极化电场方向信息;⑤利用子体极化电场信息建立每个子体的独立局部坐标系,进而定义每个子体的材料参数;⑥划分子体次级网格,定义边界条件,进行相应压电耦合分析。有限元仿真分析过程见图2。

图2 螺旋叉指电极式压电换能器有限元仿真分析过程图Fig.2 Flowchart of the finite element analysis of piezoelectric transducer with spiral interdigitated electrodes
2.2 方法优化
分析过程的核心是将换能器整体分割成一系列子体,并假定分割后的每个子体内压电特性一致,所以该方法得到的是一种近似结果。理论上分割的子体越多越接近于实际情况,但太密的分割会极大地增加有限元模型的复杂程度,计算量庞大,且子体的数量达到一定程度时,其对计算精度的提升亦有限。因此,需要综合考虑计算精度和时间两方面的因素。换能器整体的分割方法有很多,一种可行且有效的方法是根据电极的形式和极化电场的特点分割,则可在保证子体极化方向一致性的前提下减少子体数量。由于电极宽度远小于电极间距,仿真时可忽略电极的宽度以降低了建模的复杂度,而电压可直接施加在电极线对应的单元节点上形成电学边界条件。分割后的螺旋线由光滑曲线变为多线段,当划分的单元数较少时,不但难以反映出螺旋线的基本形状,同时四边形单元的较大扭曲角会进一步降低计算精度[10],因此,适当增加有效极化区域的单元密度是必要的[11]。表1反映了分割数对换能器压电耦合仿真结果的影响,其中扭转位移是静态分析得到的r=6 mm处扭转位移值,一阶扭转谐振频率和耗时由模态分析得到。由表1可知,当螺旋线的分割数达到15,次级网格单元数约为30 000时,得到的仿真结果趋于稳定;而当螺旋线的分割数>18时,模型的计算耗时将会大大增加。

表1 螺旋线分割数对压电耦合仿真结果的影响Tab.1 Influence of grid number of SIDEs on the results of piezoelectric coupling simulations
3 仿真结果和实验比较
本文仿真和实验研究选用苏州攀特电陶科技有限公司生产的PT300型高敏捷低损耗压电陶瓷,厂家给定的材料参数如表2所示,结构尺寸参数如表3所示。有限元压电耦合仿真过程使用的单元为SOLID5,几何结构和有限元网格划分如图3所示,图3(a)为初级极化电场分析时的整体结构模型(忽略中心非极化部分),图3(b)为初级极化电场分析网格,亦是压电耦合分析时重建的次级子体结构模型。优化后的初级极化电场分析的网格单元数约为3 000,次级压电耦合分析的网格单元数约为30 000。
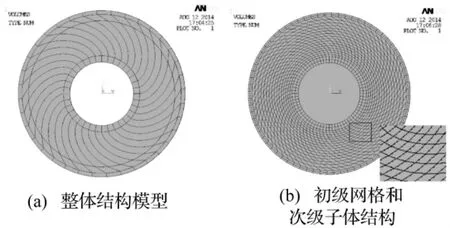
图3 螺旋叉指电极式压电换能器几何模型Fig.3 Geometricalmodels of piezoelectic transducer with spiral interdigitated electrodes

表2 压电陶瓷PT-300的材料参数Tab.2 Piezoelectric material properties of PT-300

表3 等间距螺旋电极压电圆片换能器的典型结构参数Tab.3 Typical structural parameters of the discal piezoelectric transducer w ith SIDEs of constant pitch
实验测试的换能器如图4所示,上表面的螺旋电极由激光刻蚀法加工得到,螺旋电极线的宽度为0.11 mm,螺旋线的间距为1.05 mm,下表面无电极,换能器表面涂有一层约20μm厚的绝缘胶(DP460)以隔绝外界环境保护电极,换能器牢固粘结在一个中空钢柱的上表面,固定边缘半径为12 mm。静态扭转位移由激光多普勒测振系统MLD-221测得,动态电学导纳由精密阻抗仪LCR-8101测得。

图4 等间距螺旋电极压电换能器原型Fig.4 Prototype of piezoelectric transducer with SIDEs of constant pitch between adjacent electrodes
图5为螺旋电极式换能器极化静电场分析结果,图5(a)显示等间距螺旋电极下压电换能器的电场强度云图,图5(b)显示螺旋电场方向的矢量图。在有效极化和驱动区域内,电场大小一致性较好,但受表面电极固有缺陷的影响,电极附近存在电场集中现象,使得电场大小和方向都发生了一定的变化,主要体现在两个方面:①电场集中极大地削弱了有效区域内的电场平均值;②电场在电极末端聚集,导致该区域电场的严重变形。由于驱动电场和极化电场类似,上述因素同样会作用于驱动状态,对换能器的驱动性能产生不利影响。

图5 螺旋电极式压电换能器电场分布Fig.5 Distribution of electric field for piezoelectric transducer with SIDEs
图6为静态分析得到的扭转位移结果,施加的激励电压为400 V。图6(a)显示,受电场非理想分布的影响,扭转位移并不满足严格的中心对称分布;由Saint-Venant原理,扭转位移在上下表面分布基本是一致的。图6(b)为多普勒测振平台在1 Hz频率下测得的准静态扭转位移,可以看到实测的位移曲线与静态仿真得到的结果基本吻合,换能器的最大扭转位移发生在半径r=b附近。
有限元分析得到的换能器一阶扭转振动模态的振型结果(见图7(a)),其中阻尼比设置为0.015,谐振频率为91.3 kHz。图7(b)为有限元谐响应分析和实验测试得到的导纳频率响应曲线,对应的扭转谐振点基本吻合。曲线表明,一阶扭转和三阶扭转振型对应的导纳峰值较高,二阶扭转振型由于压电应力分布相互抵消,导纳峰值表现不明显。

图6 压电换能器扭转位移径向分布特性Fig.6 Radial distribution of torsional displacements for the piezoelectric transducer with SIDEs
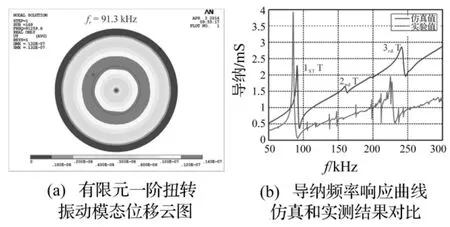
图7 换能器的动态响应特性Fig.7 Characteristics of dynamic response for the piezoelectric transducer with SIDEs
在有限元仿真结果中,位移、导纳数值与实验结果存在一定的差异,该差异来源主要有三个方面:①子体分割数量对计算精度的影响;②仿真所采用厂家给定的压电陶瓷材料参数与复杂极化条件下实际值之间的差异;③忽略电极宽度带来的影响,主要是加强了电极附近电场集中特性,从而削弱了电极中间有效区域的平均电场强度。
4 结论
螺旋叉指电极式压电圆片换能器可以产生面内扭转位移,通过坐标变换思想,给每一个子体定义局部坐标系,可以有效地建立复杂极化情况下压电换能器的有限元模型,仿真研究该类压电换能器的静动态机电耦合特性。
本文详细介绍了该有限元分析过程的操作步骤和方法优化,研究了子体划分密度对有限元仿真结果的影响,选择合适的网格划分方式,适当增加主要区域网格划分密度有助于提高有限元仿真的精度。仿真得到了静态扭转位移径向分布曲线和导纳频率响应曲线,并和实验测得的结果相比较,验证了该有限元方法的可行性和有效性。
[1]Kim J,Kang B.Performance test and improvement of piezoelectric torsional actuators[J].Smart Materials and Structures,2001,10(4):750-757.
[2]王剑,郭吉丰.径向-扭转振动复合型超声波电机的理论与实验研究[J].振动与冲击,2008,27(9):162-163.
WANG Jian,GUO Ji-feng.A radial-torsional vibration hybrid type ultrasonic motor[J].Journal of Vibration and Shock,2008,27(9):162-163.
[3]Pearce D H,Seffen K A,Button T W.Net shape formed spiral and helical piezoelectric actuators[J].Journal of Materials Science,2002,37(15):3117-3122.
[4]Pan C L,Feng Z H,Ma Y T,et al.Small torsional piezoelectric fiber actuators with helical electrodes[J].Applied Physics Letters,2008,92(1):635-640.
[5]芦志强,潘成亮,马玉婷.基于螺旋叉指电极的压电圆盘扭转致动器[J].压电与声光,2010,32(5):758-761.
LU Zhi-qiang,PAN Cheng-liang,MA Yu-ting.Piezoelectric disk torsional actuator with spiral interdigitated electrodes[J].Piezoelectrics and Acoustooptics,2010,32(5):758-761.
[6]刘祥建,陈仁文.Rainbow型压电换能结构的有限元分析与实验[J].光学精密工程,2011,19(4):789-796.
LIU Xiang-jian,CHEN Ren-wen.Finite elementanalysis and experiments on rainbow shape piezoelectric energy transferring elements[J].Optics and Precision Engineering,2011,19(4):789-796.
[7]卢义刚,颜振方.Cymbal压电发电换能器的有限元分析[J].振动与冲击,2013,32(6):157-162.
LU Yi-gang,YAN Zhen-fang.Finite element analysis on energy harvesting with cymbal transducer[J].Journal of Vibration and Shock,2013,32(6):157-162.
[8]Agbossou A,Pan C L,Zhang Q,et al.Piezoelectric tube with helical electrodes:Numerical analysis of actuator and energy harvesting devices[J].Journal of IntelligentMaterial Systems and Structures,2013,24(10):1245-1256.
[9]栾桂冬,张金铎,王仁乾.压电换能器和换能器阵[M].修订版.北京:北京大学出版社,2005.
[10]李海峰,吴冀川,刘建波,等.有限元网格剖分与网格质量判定指标[J].中国机械工程,2012,23(3):368-377.
LI Hai-feng,WU Ji-chuang,LIU Jian-bo,et al.Finite elementmesh generation and decision criteria ofmesh quality[J].China Mechanical Engineering,2012,23(3):368-377.
[11]宋少云,尹芳.有限元网格划分中的圣维南原理及其应用[J].机械设计与制造,2012,8:63-65.
SONG Shao-yun,YIN Fang.Sain vaint principle of meshing in finite elementmethod and its application[J].Machinery Design and Manufacture,2012,8:63-65.
Finite element analysis and comparison between simulation and test for a discal piezoelectric transducer w ith spiral interdigitated electrodes
XIAO Guang-jun1,PAN Cheng-liang2,LIU Yong-bin1,3,PAN Qiao-sheng1
(1.School of Engineering Science,University of Science and Technology of China,Hefei230026,China;
2.School of Instrument Science and Opto-electronic Engineering,Hefei University of Technology,Hefei230009,China;
3.College of Electrical Engineering and Automation,Anhui University,Hefei230039,China)
A piezoelectric disk with spiral interdigitated electrodes(SIEDs)can produce in-plane torsion with advantages of simple structure,convenientmanufacture,and reliable performance,it can be applied in ultrasonicmotors,optical scanners,viscometers,and many others.However,because of the complex variation of polarizing direction of piezoceramic material between surfaces SIEDs,great difficulties are brought for electromechanical coupling analysis and optimal design of the transducer.Here,utilizing the idea of coordinate transformation with the aid of the finite element method,the piezoelectric disk was divided into a number of sub-volumes.The material parameters were defined in the local coordinate systems determined with the analysis of polarized electric field.Thus,the coupling simulations of the piezoelectric transducer were achieved under the complex polarization conditions.The simulation processeswere optimized with the finite element software ANSYS,the radial distribution of static torsional displacement and the frequency response features of dynamic admittance of the transducer were investigated.Comparing the simulation results with the test ones,the feasibility and effectiveness of the proposed method were validated.
piezoceramic;discal transducer;spiral interdigitated electrodes;in-plane torsion;finite element simulation
TH212;TH213.3
A
10.13465/j.cnki.jvs.2015.23.023
国家自然科学基金资助课题(51205338);中国博士后科学基金面上与特别资助项目(2014M561818,2013T60620)
2014-10-23修改稿收到日期:2014-12-26
肖广军男,硕士,1989年生
潘成亮男,博士,副研究员,1983年生
