一种滚动轴承振动信号的数据压缩采集方法

郭俊锋，施建旭，雷春丽，魏兴春

(兰州理工大学机电工程学院，兰州730050)

一种滚动轴承振动信号的数据压缩采集方法

郭俊锋，施建旭，雷春丽，魏兴春

(兰州理工大学机电工程学院，兰州730050)

针对目前滚动轴承振动信号频带越来越宽，依据传统香农－内奎斯特采样定理进行数据采集时，将会得到巨量振动数据，对存储、传输和处理带来困难的问题，提出了一种滚动轴承振动信号的数据压缩采集方法。首先分析了振动信号在正交字典傅里叶基上的近似稀疏性，即可压缩性;然后融入振动信号在傅里叶基上稀疏性的结构信息，得到其优化的测量矩阵并进行压缩测量;最后基于压缩测量值采用正交匹配追踪算法对原始振动信号进行重构。通过仿真试验，结果表明，该方法既可以得到较高的信号压缩比又有着精确的信号重构性能，在不丢失振动信息的情况下，大大减少了原始振动数据量。

滚动轴承;振动信号;压缩测量;测量矩阵;正交字典

滚动轴承是机械、电力、石化、冶金、航空航天以及军事工业重要的且最常用的零件之一，其工作状态正常与否直接影响到设备的性能。滚动轴承振动信号蕴含着丰富的设备运行过程中的重要信息，检测振动信号能够了解和掌握机械设备在使用过程中的状态，是提高设备运行的可靠性、安全性、有效性和管理水平的前提，也可以为设备结构优化、合理制造以及生产过程提供数据信息，因此，检测振动信号具有重要的现实意义和经济价值。

传统滚动轴承转速较低，其振动信号频带也较窄，但是，随着工业技术的飞速发展，机械设备日趋高速高效，而作为设备支撑件之一的滚动轴承，其转速也越来越高，致使滚动轴承振动信号的频带也越来越宽，依据传统香农－内奎斯特采样定理对滚动轴承振动信号进行检测采样将会得到巨量数据，这些数据的实时传输与同步存储已成为亟待解决的成本与工程技术瓶颈问题，尤其在远程设备状态监测领域，这些巨量的采集数据对传输造成了巨大压力［1］。

针对上述问题，提出了一种压缩测量方法，该方法是建立在振动信号具有稀疏性的基础上，其压缩测量的每个振动数据均具有振动信号的全局性信息，其测量过程为，首先对振动信号进行稀疏分解;然后压缩测量;最后在数据处理端，进行振动信号测量信息的重构。这种方法经过仿真试验，在不损失振动信息的情况下，大大减少了数据量。

1 经典的基于Shannon－Nyquist的振动信号数据采集压缩分析

经典的Shannon－Nyquist振动信号采集理论［2］，要求采集频率高于振动信号最高频率的2倍，对采集后的振动信号采用线性加权能实现原始振动信号的精确重构。随着振动信号频带的加宽，基于经典的信号采集理论会得到巨量的振动数据，为了传输、存储和后期处理的方便，将采集的振动信号数据进行传统的数据变换压缩，这种采集后再压缩信号的方法效率较低，经典的振动信号采集理论是基于信号带宽的，Nyquist采集率是恢复原始振动信号的充分条件并不是必要条件，如果利用振动信号的其他特性，可以降低采集率，提高效率，经典采集理论具体过程见图1。

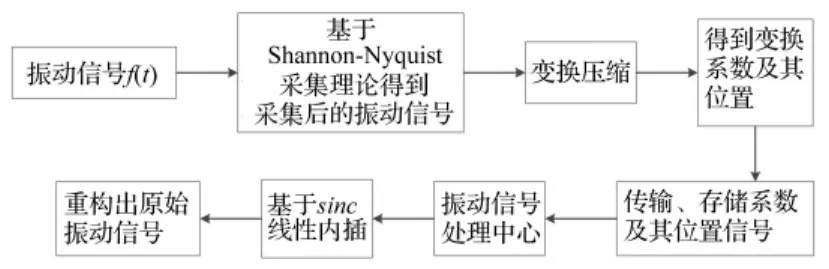
图1 经典的振动信号采集压缩原理Fig.1 The classic principle of vibration signal acquisition and compression

2 基于振动信号稀疏性的数据压缩采集方法

振动信号的带宽和稀疏性都是信号的先验条件，基于振动信号带宽的采样会产生大量的振动数据，而基于信号的稀疏性，能够实现信号有用信息的高效获取(见图2)。

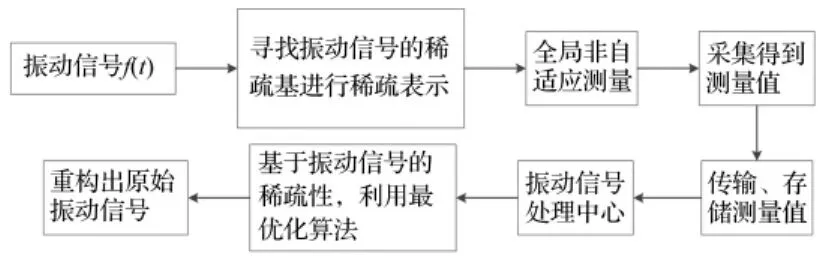
图2 基于稀疏性的振动信号压缩采集原理Fig.2 The acquisition and compression principle of basing on vibration signal's sparsity

2.1 振动信号的稀疏性分析

信号在稀疏变换域上只有k个非零元素属于绝对稀疏的情况，一般情况下信号不一定满足绝对稀疏的要求，但是信号的稀疏变换系数经过指数排列衰减趋于零时，信号可以认为是近似稀疏表示的信号［3－4］，即可压缩信号。滚动轴承振动信号中包含了多种余弦信号和冲击衰减信号，其频谱相对于时域原始振动信号是理想的近似稀疏信号。

滚动轴承振动信号的整体特征一般可用其工频及其主要倍频和分频来表征［5］，且当轴承发生故障时还会出现调幅振动和冲击振动，建立轴承外圈振动信号模型:

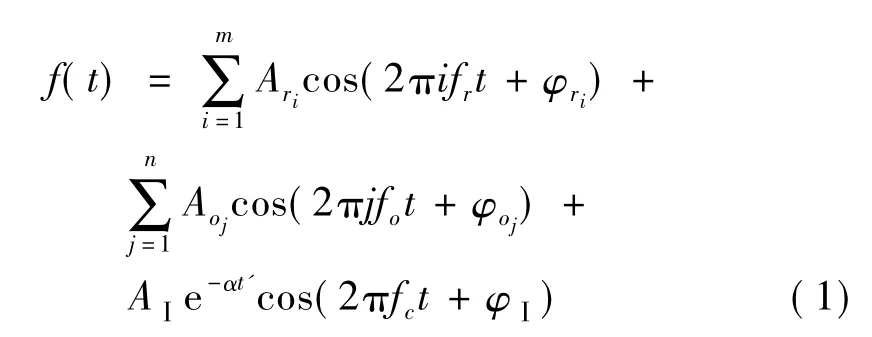
以轴承型号6205－2RS为例，取其内径d1、外径d2、滚动体直径d3、接触角β和个数z分别25 mm、52 mm、7.9 mm、0.67 rad和9，转频fr=30 Hz，采样频率fs=1 024 Hz，则根据外圈故障频率的计算公式:

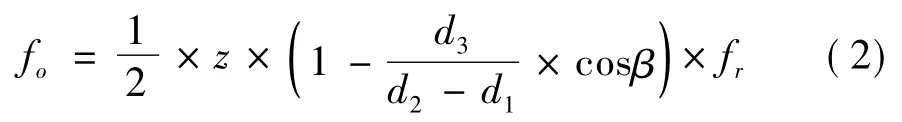
得到其外圈故障频率fo=104.03 Hz，设外圈发生故障时激发的载波频率fc=3 000 Hz。m=3，n=5，Ari(i=1，2，3)、Aoj(j=1，2，3，4，5)和AⅠ分别为0.1、0.2、0.3、0.3、0.4、0.33、0.2、0.1、0.38，φri(i=1，2，3)、φoj(j=1，2，3，4，5)和φⅠ分别为0、3、2.5、0、2、6、4、4.5、3.3，衰减系数α为800。则轴承6205－2RS的外圈振动信号模型具体化为:

前三项为轴承的3次谐波振动，四至八项为轴承外圈发生故障时的5次谐波振动，最后一项为轴承外圈发生故障时产生的冲击衰减振动。

振动信号的时域波形(见图3(a))，傅里叶变换后得到的系数(见图3(b))。从图3(b)和表1可知，大部分DFT系数是小系数，只有小部分系数数值较大，将DFT系数的绝对值从大到小排序后的结果(见图3(c))，排序后的系数以指数方式衰减且趋于零，这说明了滚动轴承振动信号在傅里叶基上是近似稀疏的。

2.2 振动信号的测量矩阵设计

测量矩阵是得到原始振动信号测量值及其重构的关键，其性能直接影响着振动信号的压缩测量能否成功实现。融入振动信号在正交字典傅里叶基上稀疏性的结构信息到测量矩阵的设计中，得到其最优的测量矩阵能够显著提升压缩测量性能。

2.2.1 振动信号的压缩测量性能分析

设f∈Rn是一个原始振动信号，在正交变换傅里叶基Ψ∈Rn×n上具有很好的稀疏性，这是由振动信号的结构信息决定的，即，用一个测量矩阵Φ∈Rm×n(m∩n)将原始振动信号f∈Rn投影到低维空间Rm中的一个测量向量y∈Rm，如果已知Ψ，Φ和y就可以利用重构算法高概率地重构出原始振动信号x，即求解如下的最优化问题:

D=ΦΨ记为感知矩阵，D必须满足零空间特性(NSP)，即D的零空间中不能包含稀疏度为2k的振动信号，才能重构稀疏度为k的两个不同的振动信号。但是，要验证一个矩阵是否满足NSP是一个NP难题，为了寻求更容易操作的条件，因此，产生了很多等价形式，其中最著名的理论之一是Spark理论［6］，当且仅当Spark(D)＞2k时，能从某一测量值中最多恢复一个与其对应的某一原始振动信号，然而，NSP和Spark都没有考虑测量值中含有噪声的情况，Tao等［7］提出了约束等距特性(RIP)。要验证和设计出的矩阵D满足NSP、Spark和RIP其中的一个，都是一个NP难题，为了避开NP难题，Tropp等［8］提出了矩阵D的相干性。近年来相关领域研究表明，互相干系数影响着重构效果和测量值的数目，互相干系数越小，重构信号时需要的测量值数目越少，信号适应的稀疏度范围越大，因此，通过减少测量矩阵与稀疏变换基之间的互相干系数能够提高重构性能，即使得感知矩阵D=ΦΨ有很小的列向量互相干系数μ，即

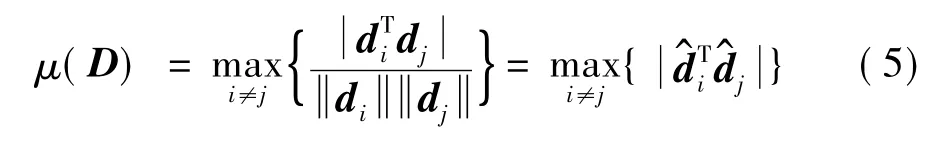
式中:di和(i=1，2，…，n)分别表示感知矩阵D和其经过列单位化得到的D的列向量。设

式中:G称为压缩感知矩阵D的Gram矩阵，互相干系数可以等价定义为矩阵中非对角线元素的最大值，即

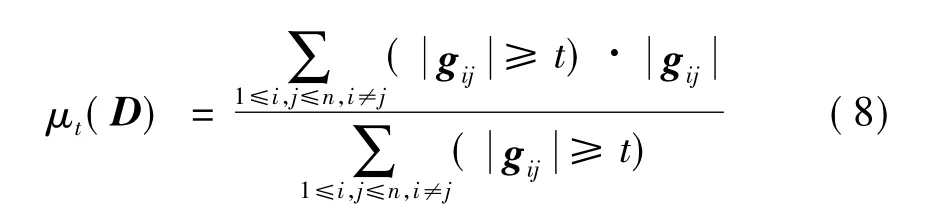
表1 傅里叶系数分布Tab.1 Fourier coefficients distribution

互相干系数度量了压缩感知矩阵D的列向量之间的最大相关性，并且在重构算法里起着重要的作用，理论证明μ需要尽可能小。

从上面的分析可知，处理振动信号时，寻找到与傅里叶稀疏变换基相干性最优测量矩阵，可以提高压缩测量性能。

2.2.2 振动信号在傅里叶基上的最优测量矩阵设计

根据最优测量理论，其设计过程是:已知傅里叶基Ψ、初始测量矩阵、阈值t和尺度下降因子γ，得到使得μt{D=ΦΨ}最小的矩阵Φ∈Rm×n作为测量矩阵，称此时的Φ为傅里叶稀疏变换基对应的最优测量矩阵。

基于最优测量矩阵构造算法［11］，得到振动信号的最优测量矩阵如下:

输入参数:傅里叶稀疏变换基ΨDFT∈Cn×n，测量矩阵Φ∈Rm×n的初始值Φ0为一个任意的高斯随机矩阵或托普利兹矩阵，令压缩感知矩阵D=ΦΨ，t表示阈值，γ表示尺度下降因子(0＜γ＜1)，m表示测量次数，Iter表示迭代次数，循环变量k，初始值k=0。

具体步骤:

步骤1根据振动信号在傅里叶基上的稀疏性，确定测量矩阵Φ的行数

步骤2计算感知矩阵D=ΦΨ

步骤5根据阈值t更新Gk，按如下关系得到矩阵

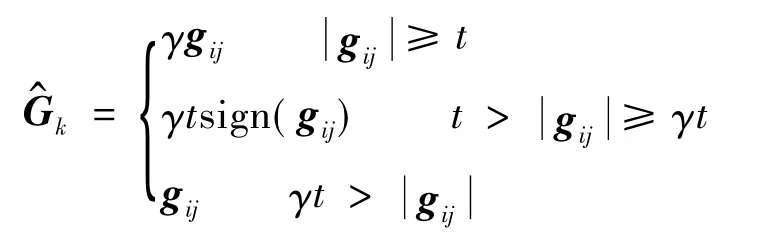
步骤7求解Dk，Dk是m×n矩阵，G^k=DD k，通过感知矩阵得到经过一次迭代的振动信号优化测量矩阵

步骤9 k=k+1，直到k=Iter，循环结束

输出:ΨDFT对应的最优测量矩阵ΦDFT

整个流程见图4。

在上面的具体步骤中，初始测量矩阵与傅里叶稀疏变换基作乘积得到感知矩阵，对感知矩阵进行处理，最后再通过感知矩阵求得优化的测量矩阵，这样就把振动信号在傅里叶基上的稀疏性结构信息融入到了测量矩阵的设计中，并最终得到振动信号在傅里叶基上对应的最优测量矩阵。

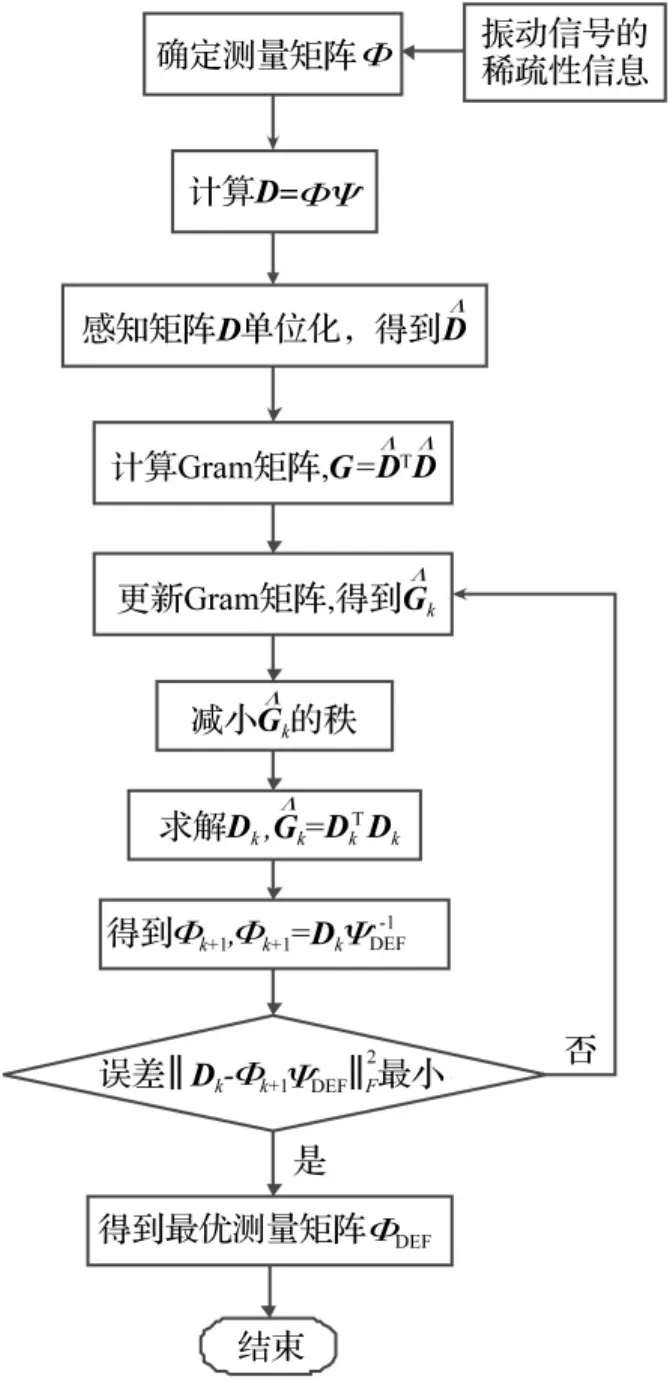
图4 振动信号的最优测量矩阵构造流程图Fig.4 A flow chart of constructing optimal measurementmatrix of vibration signal

3 仿真试验

试验对象为轴承型号6025－2RS，该轴承外圈振动信号模型为式(3)，信号长度为512×1的向量，稀疏变换基为512×512的傅里叶正交变换矩阵，测量矩阵为高斯随机矩阵、托普利兹矩阵以及融入振动信号得到的最优测量矩阵，根据压缩测量重构条件，测量值数目m至少是两倍的稀疏度k，即m≥2k，经过振动信号的稀疏性分析以后，稀疏度k=134，因此重构需要的测量值数最小为268，为进行验证，仿真试验测量值数目分两段选取，一段取为＜268的测量值数，即250和260，另一段取≥268的测量值数，即268，270，272，…，296序列，重构算法采用正交匹配追踪算法OMP。

仿真试验从两方面分析了振动信号的压缩测量性能，即重构效果和压缩比。

从重构效果来看，图5、图6和表2表明相对误差随测量值数的整体发展趋势，高斯随机测量矩阵在优化前后都能精确重构原始振动信号，而托普利兹矩阵在优化之前不能重构原始振动信号，在优化以后能精确重构振动信号，具体的测量值数目和对应的相对误差(见表2)，当m＜268时，相对误差很大，m=268时，相对误差就急剧减小，达到近似精确重构，而m＞268时，相对误差会逐渐减少但变化非常小且测量值数目增多带来计算量增大，仿真试验进一步验证了压缩测量重构条件，最终从相对误差和计算量两方面综合考虑得到最优的测量值数目是268，总之，优化测量矩阵的性能明显高于未优化测量矩阵，得到最优适合振动信号的测量矩阵。

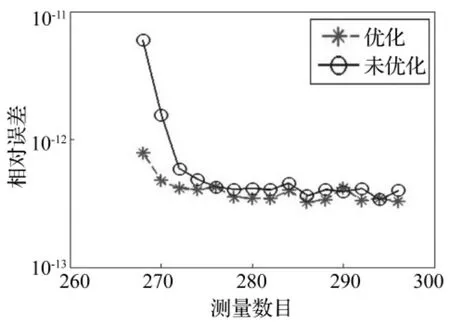
图5 高斯随机矩阵优化前后，相对误差是测量数目的函数Fig.5 Relative errors as a function of the numbers of measurements，with Gauss random matrix and optimized matrix

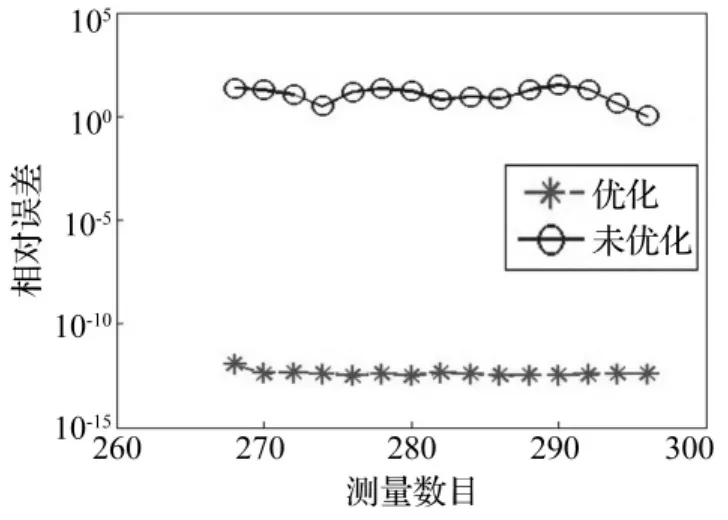
图6 托普利兹矩阵优化前后，相对误差是测量数目的函数Fig.6 Relative errors as a function of the numbers of measurements，with Toeplitzmatrix and optimized matrix

表2 相对误差Tab.2 Relative errors

从压缩比来看，测量值数目与原始振动信号数据量之比为0.523 4～0.578 1，有较高的振动信号压缩比，并且能通过压缩测量值近似精确重构出原始振动信号，仿真试验仅采用了较少的数据量，当随着数据量的剧增，形成巨量数据，提出的振动信号压缩采集方法能有效减少原始数据量且不会丢失振动信息。

进一步分析未优化测量矩阵和优化测量矩阵对振动信号的压缩测量性能可知，高斯随机矩阵在优化前后都能够精确重构出原始振动信号，但是，经过优化的高斯随机测量矩阵性能明显高于未优化的，尤其是在测量值数目较少的情况下，其重构误差更小，这是因为高斯随机测量矩阵与正交稀疏变换基不相干，经过最优测量算法优化以后，性能会进一步提升;托普利兹矩阵是确定性测量矩阵，未优化之前，其对傅里叶稀疏变换基的相关程度较大，因此，用于压缩测量处理振动信号时，不能重构出原始振动信号，而融入振动信号的结构信息经过优化以后，使其对傅里叶稀疏变换基的相关程度大大减少，能够近似精确重构出原始振动信号。因此，最优测量矩阵算法能够得到滚动轴承振动信号在傅里叶基上的最优测量矩阵，达到了明显改善振动信号压缩测量性能的目的，是一种全新的振动信号压缩采集方法。

在相同的试验条件下，采用经典的振动信号采集压缩方法进行仿真试验，并对信号的重构质量进行了比较，图7和图8分别给出了经典的振动信号采集压缩重构结果和基于振动信号稀疏性的压缩采集重构结果。

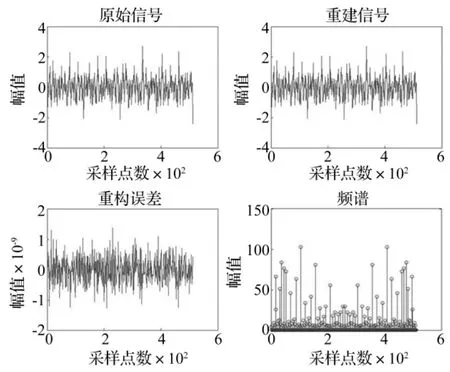
图7 经典的振动信号采集压缩重构结果Fig.7 Vibration signal reconstruction results of classic acquisition and compression

从图7、图8和表3对比分析可知，基于振动信号稀疏性的压缩采集，对信号整体的测量保留了信号的有用信息，是对振动信号的全局测量，在测量值数量大于振动信号精确重构需要的最小值时，如果在传输或存储发生意外而丢失了个别测量也不会影响振动信号的精确重构，因此在重构过程中有更高的重构精度。

经过以上的仿真试验分析，滚动轴承振动信号的压缩采集方法能够有效解决巨量振动数据，对存储、传输和处理带来困难的问题。

表3 重构误差Tab.3 Reconstruction errors

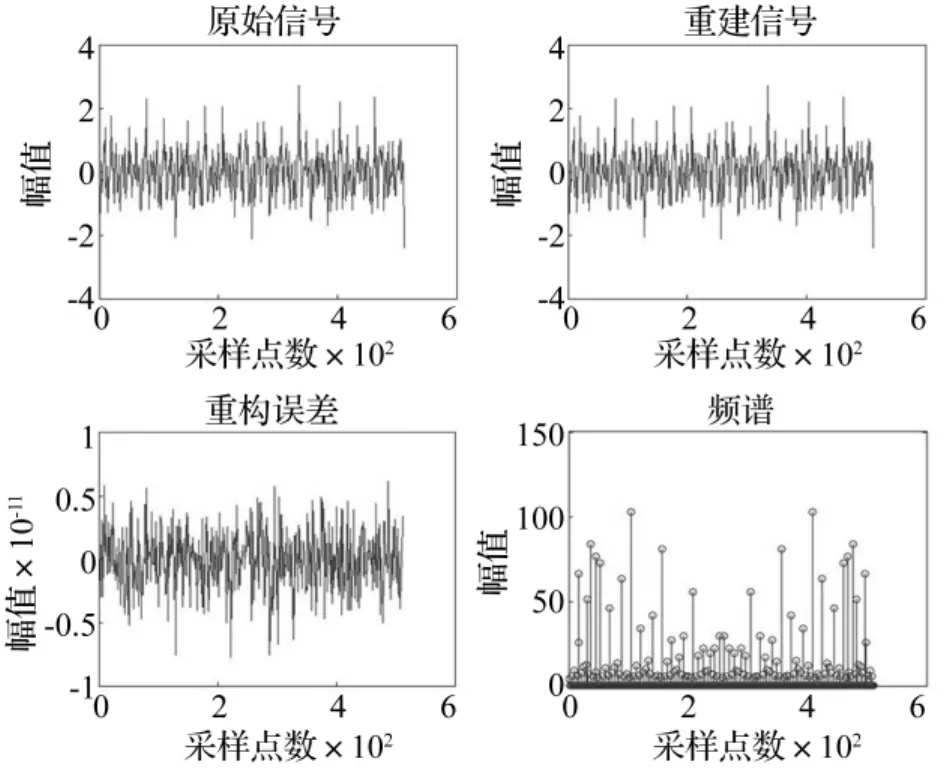
图8 基于振动信号稀疏性的压缩采集重构结果Fig.8 Vibration signal reconstruction results of basing on sparsity compression and acquisition

4 结论

针对巨量的振动数据，对存储、传输和处理带来困难的问题，提出了一种振动信号的数据压缩采集方法，通过试验分析了振动信号在傅里叶基上的稀疏性，融入振动信号在傅里叶基上稀疏性的结构信息到其测量矩阵的设计中，得到适合振动信号的测量矩阵并进行压缩采集，在不丢失振动信号信息的情况下，大大减少了原始振动数据量。压缩测量值可以重构原始振动信号，进行传统的处理分析，也可以直接从压缩测量值中提取信息。

［1］蔡巍巍，汤宝平，黄庆卿.面向机械振动信号采集的无线传感器网络节点设计［J］.振动与冲击，2013，32(1):73－78.

CAIWei－wei，TANG Bao－ping，HUANG Qing－qing.Design of wireless sensor network node for collecting mechanical vibration signals［J］.Journal of Vibration and Shock，2013，32，(1):73－78.

［2］余恺，李元实，王智，等.基于压缩感知的新型声信号采集方法［J］.仪器仪表学报，2012，33(1):105－112.

YU Kai，LI Yuan－shi，WANG Zhi，et al.New methodfor acoustic signal collection based on compressed sa－mpling［J］.Chinese Journal of Scientific Instrument，2012，33(1):105－112.

［3］Donoho D.Compressed sensing［J］.IEEE Transaction on Information Theory，2006，52(4):1289－1306.

［4］Candes E，Romberg J，Tao T.Robustuncertainty principles: exact signal reconstruction from highly inco－mplete frequency information［J］.IEEE Transactions on Information Theory，2006，52(2):489－509.

［5］吴斌，王敏杰，康晶，等.滚动轴承故障振动信号特征与诊断方法［J］.大连理工大学学报，2013，53(1):76－81.

WU Bin，WANG Min－jie，KANG Jing，et al.Fault vibration signal feature of rolling bearing and its diagnosismethod［J］.Journal of Dalian University of Technology，2013，53(1):76－81.

［6］Donoho D，Elad M.Optimally sparse representation in general (non－orthogonal)dictionaries via▮1minimization［J］.Proceedings of National Academy of Sciences of the United States of America，2003，100(5):2197－2202.

［7］Candes E，Tao T.Decoding by linear programming［J］.IEEE Transactions on Information Theory，2005，51(12):4203－4215.

［8］Tropp J，Gilbert A.Signal recovery from partial inf－ormation via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53(12):4655－4666.

［9］赵瑞珍，秦周，胡绍海.一种基于特征值分解的测量矩阵优化方法［J］.信号处理，2012，28(5):653－658.

ZHAO Rui－zhen，QIN Zhou，HU Shao－hai.An optimization method for measurement matrix based on eigenvalue decomposition［J］.Signal Processing，2012，28(5):653－658.

［10］Elad M.Optimized projections for compressed sensing［J］.IEEE Transactions on Signal Processing，2007，55(12):5695－5702.

［11］Candes E，Wakin M.An introduction to compressi－ve sampling［J］.IEEE Signal Processing Magazine，2008，25 (2):21－30.

Data com pression method for collecting rolling bearing vibration signals

GUO Jun－feng，SHIJian－xu，LEIChun－li，WEIXing－chun
(School of Mechanical and Electronic Engineering，Lanzhou University of Technology，Lanzhou 730050，China)

Aiming at that frequency band of rolling bearing vibration signals is getting wider，with the traditional Shannon－Nyquist sampling theorem for data collection，a huge amount of data will be obtained to cause difficulties of storage，transmission and processing，a data compression and acquisition method was proposed here.Firstly，the sparsity or compressibility of vibration signals based on Fourier bases in the orthogonal dictionary was analysed，then the sparse structure information of vibration signalswasmixed into the design of themeasurementmatrix，the optimizedmeasurement matrix was gained and the compression measurement was done.Finally，based on the compression measurements，the orthogonalmatching pursuit algorithm was used to reconstruct the original vibration signals.Through simulation tests，the results showed that the proposed method can get a higher signal compression ratio and have a precise signal reconstruction performance;in the condition without losing vibration information，the data amount of the original vibration can be reduced greatly.

rolling bearing;vibration signal;compressed sensing;measurementmatrix;orth－ogonal dictionary

TH17

A

10.13465/j.cnki.jvs.2015.23.002

国家自然科学基金资助项目(51465034，51465035)

2014－09－22修改稿收到日期:2014－11－28

郭俊锋男，博士，副教授，1978年生

施建旭男，硕士生，1989年生