高雷诺数范围内不同形状柱体流致振动特性研究

丁 林，张 力，姜德义

（1．重庆大学低品位能源利用技术及系统教育部重点实验室，重庆 400044；2．重庆大学资源及环境科学学院，重庆 400044）

高雷诺数范围内不同形状柱体流致振动特性研究

丁 林1，2，张 力1，姜德义2

（1．重庆大学低品位能源利用技术及系统教育部重点实验室，重庆 400044；2．重庆大学资源及环境科学学院，重庆 400044）

流致振动是自然界和工程领域中普遍存在的一种流固耦合现象，其流固耦合过程非常复杂，涉及许多科学上的难题，一直是国际前沿研究热点之一。针对不同截面形状柱体的流致振动进行数值计算，研究高雷诺数范围内（30 000≤Re≤110 000）柱体流致振动特性，分析柱体振幅、频率和尾迹旋涡形态。结果表明，粗糙表面圆柱和类梯形柱Ⅰ的的流致振动响应强于其他形状柱体，最大振幅达到3．5D。圆柱、方柱、三角柱和类梯形柱Ⅰ的流致振动随来流速度变化均观察到明显的涡致振动初始分支、上部分支和驰振。类梯形柱Ⅱ出现高频低幅振动，未观察到明显的振动分支。另外，柱体流致振动振幅和频率与尾迹旋涡形态紧密相关，在不同的振动分支，尾迹呈现出不同的旋涡形态。

流致振动；旋涡脱落；涡致振动；驰振

钝体是工程中一种常见的非流线型结构，在一定的流速下，流体绕流钝体后会在钝体两侧交替地产生脱离钝体表面的旋涡，旋涡脱落会在结构表面形成复杂且不稳定的作用力，当钝体固定方式为弹性支撑或允许发生弹性形变时，流体绕流产生的作用力将引起钝体结构的振动，同样钝体的振动会反过来影响周围的流场，改变流体作用力，引起流体和钝体结构的相互耦合，由于流体与钝体之间相互作用而产生的结构振动即流致振动［1］。

在许多与流体有关的机械与工程中，流致振动是一个涉及安全性的重大问题，随着近年来海洋工程、风工程、航空航天和核工程等的发展，关于钝体流致振动的问题受到广泛地关注，例如反应堆、高大建筑物、海洋平台、海洋立管等都涉及到此类问题［2－3］。其中，涡致振动（VIV）和驰振（Galloping）是最为常见的两种流致振动现象。另外，目前已有学者将流致振动与发电技术相结合，将流动能转换为有用的电能，使这种潜在的破坏性现象得到有效利用，提高了自然界中可再生能源利用范围［4］。因此，对于钝体流致振动问题的研究具有非常重要的学术意义与应用价值。

由于流致振动是一个异常复杂的流固耦合过程，目前相关研究大都以实验为主，而且主要集中于圆柱和方柱振子模型，对于其他截面形状钝体流致振动的研究报道有限，高雷诺数（Re）流致振动的数值模拟研究报道更少。近年来，关于圆柱涡致振动的代表性综述主要有Williamson和Govardhan［1］，Bearman［5］等。任安禄等［6］对Re＝250时的方柱流致振动特性进行研究，发现在振子系统阻尼比和质量比相同时，驰振的振幅远大于涡致振动振幅。Nemes等［7－8］研究了低Re数下不同攻角绕流方柱的流致振动特性，研究发现具有攻角的方柱会在流场中失去对称性，产生更为复杂的尾流模式。Kumar等［9］则研究了方柱的四个棱角倒成圆角后的流致振动特性，发现倒角半径对尾流结构和振动稳定性产生较大影响。徐枫等［10］对不同截面柱体在低Re数下的流致振动进行了数值分析，发现在Re＝200时，不同截面柱体表现出不同的流致振动形式。可见，钝体几何特征是影响流致振动的一个关键影响因素，钝体的截面形状不同，其流致振动特性也会有很大差别。

本文针对不同截面形状柱体的流致振动问题进行研究，包括圆形、方形、三角形和类梯形等截面形状。采用数值方法研究了高雷诺数（30 000≤Re≤110 000）下柱体流致振动特性，详细分析了不同形状柱体振幅、频率和尾迹旋涡形态，探讨了各种因素对柱体后旋涡脱落的影响，并将各种形状柱体流致振动的振幅和频率的变化规律进行对比。

1 物理模型

由于发生流致振动的柱体在流向的振幅远小于横向振幅，因此本文仅对横向振动进行研究，即将柱体流致振动模型假设为单自由度质量－弹簧－阻尼系统。本文采用数值方法对柱体的流致振动特性进行研究，物理模型见图1，支撑弹簧的弹性系数为k，系统阻尼为c。柱体截面形状包括圆形、方形、三角形和类梯形，各柱体沿流向的投影长度均为D（D＝0．088 9 m），详细特征如下所述：

（a）圆柱：由于当Re＞12 000时，采用RANS方法求解光滑圆柱流致振动时，流动分离点将固定在圆柱上下点（±90°），结果误差较大，因此，本文将圆柱表面安装两条粗糙面PTC，粗糙面位置如图1中圆柱模型所示，αPTC＝20°，PTC宽度为16°，厚度0．847 mm；

（b）方柱：采用正方形截面柱体，边长为D；

（c）三角柱：采用正三角形截面柱体，边长为D，三角柱一底面设为迎风面；

（d）类梯形柱：柱体长边为D，短边为0．5D，上下棱边长0．25D，当类梯形柱长边为迎风面时记为类梯形柱Ⅰ，类梯形柱短边为迎风面时记为类梯形柱Ⅱ。

图1 物理模型Fig．1 Physicalmodel

本文数值计算中各个钝体采用相同的系统阻尼和弹性系数，流动工质为15℃的液态水，详细的系统参数见表1。

表1 系统参数Tab.1 System parameters

2 数值方法

通过求解非稳态雷诺平均纳维－斯托克斯方程组（Unsteady Reynolds-averaged Navier-Stokes，URANS），获得绕流弹性支撑柱体流场的数值解。不可压缩流体连续性方程和动量方程为：

式中：Ui为平均流速，τij＝－ρui′uj′是 雷诺应力张量，ν为分子运动粘度，Sij为应变率张量

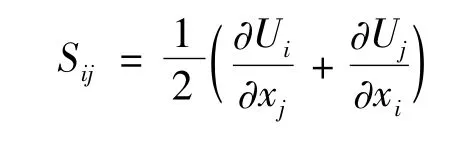
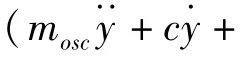
本文计算区域尺寸为50D×50D，柱体位于流场中心，见图2。入口边界Inflow假定为均匀流速，出口Outflow设定为压力出口。由于上下侧面（Top和Bottom）与柱体距离较大，假设不受柱体影响，采用与入口边界相同的条件。柱体壁面采用运动壁面边界条件。本文计算区域整体采用结构化网格，近壁面区域进行网格加密。为了解本文得出的数值解受网格疏密程度的影响，针对各种不同截面的柱体，分别选取疏密不同的三种网格进行绕流计算。表2所示为Re＝1．4×105时的圆柱绕流网格无关性验证结果，将计算得到的阻力系数CD、升力系数CL与他人早期的研究结果进行对比，本文计算结果与他人研究结果吻合较好，三种网格得出的结果相近，因此，本文最终计算采用中等网格。值得注意的是，本文采用壁面函数处理近壁计算，对于不同Re数，中等网格能使y+处于30～70范围内，满足壁面函数求解要求。其他截面形状柱体均采用类似方法进行了网格无关性验证。类梯形柱壁面区域网格见图3。

图2 计算区域及边界条件Fig．2 Computational domain and boundary conditions

表2 Re＝1.4×105时圆柱网格无关性验证Tab.2 Grid Resolution study for circular cylinder（Re＝1.4×105）

图3 类梯形柱近壁面中等网格示意图Fig．3 Close-up of themedium grid for a quasi-trapezoid cylinder

3 结果与讨论

本文针对不同形状柱体流致振动问题进行数值分析，物理模型包括圆形、方形、三角形和类梯形等截面形状。运用有限体积法，采用基于URANS的Spalart-Allmaras湍流模型，研究高雷诺数（30 000≤Re≤110 000）下柱体流致振动特性。详细分析了不同形状柱体振幅、频率和尾迹旋涡形态，探讨了各种因素对柱体后旋涡脱落的影响，将各种形状柱体流致振动的振幅和频率的变化规律进行比较分析。

3.1 振幅响应

图4为不同截面柱体的振幅率随Re变化的曲线，并与Chang［13］的光滑圆柱实验结果进行比较。从图中可以看出，类梯形柱Ⅱ的振幅率曲线与其他柱体的数值结果有所不同，在所研究的整个Re范围内并未观察到明显的振动分支，振幅均低于其他柱体，最大振幅仅为0．2D。然而，圆柱、方柱、三角柱和类梯形柱Ⅰ的流致振动振幅率曲线均出现了几个不同的振动分支，分别是VIV初始分支（Re＜50 000）、VIV上部分支（50 000≤Re＜80 000）、VIV－驰振过渡分支（80 000≤Re＜100 000）和驰振（Re≥100 000）。

在VIV上部分支，柱体振幅随Re变化较小，圆柱、三角柱和类梯形柱Ⅰ的振幅达到了1．5D。在相同Re数下，类梯形柱Ⅰ的振幅率均高于其他柱体。方柱振幅相对较小，维持在1D附近。

图4 不同截面柱体振幅率随Re数变化Fig．4 Amplitude ratio comparison of the cylinderswith different cross sections

另外，在Chang［13］的光滑圆柱实验结果中，当柱体达到VIV上部分支后，随着Re进一步增加，VIV由上部分支过渡到下部分支。然而，本文粗糙表面圆柱、方柱、三角柱和类梯形柱Ⅰ的驰振在Re＞80 000时受到激发，并没有出现VIV下部分支，柱体振幅随着Re增加而急剧增大。当驰振发生时，圆柱和类梯形柱Ⅰ的最大振幅均达到了3．5D。

3.2 频率响应

图5为圆柱、方柱、三角柱和类梯形柱Ⅰ的流致振动频率比fosc／fn，water随Re的变化趋势，同样可分为VIV初始分支、VIV上部分支、VIV－驰振过渡区域和驰振。在VIV初始分支，频率比随Re数增加而上升；频率比在VIV上部分支达到最大值，当柱体发生驰振时，频率随流速增加而降低。这点与Chang［13］的实验结果不同，当光滑圆柱VIV过渡到下部分支时，振动频率随Re增加而增加。方柱和三角柱的振动频率相对较低，圆柱和类梯形柱Ⅰ的振动频率比在Re＞50 000后维持在1附近，柱体产生共振。结合图4可知，在相同Re数下，类梯形柱Ⅰ的振幅率均高于其他柱体，因此，类梯形柱Ⅰ的流致振动响应优于其他柱体。与其他柱体有所不同，其频率比出现单调上升的变化趋势，而且高于所研究的其他各类柱体，频率比从1．12（Re＝30 000）逐渐增加到3．98（Re＝110 000），流致振动出现了高频率、低振幅的特征。

图5 不同截面柱体频率比随Re数变化Fig．5 Frequency ratio comparison of the cylinders with different cross sections

3.3 尾迹旋涡形态

为了对不同截面形状柱体的流致振动响应特性进行深入了解，本文对柱体尾迹旋涡形态进行了详细分析，探讨各类柱体流致振动振幅和频率响应产生差异的原因。

图6所示为粗糙表面圆柱不同振动分支时的尾迹旋涡图，选取了三个具有代表性的Re数进行分析，分别对应VIV初始分支（Re＝30 000）、VIV上部分支（Re＝60 000）和VIV－驰振过渡分支（Re＝90 000）。Re＝30 000（U*water＝5．54）时，圆柱尾迹旋涡形态为典型的2S模式，其中S（Single）表示单个旋涡。2S模式类似于经典的卡门涡街，在一个振动周期内，随着圆柱上下振动，两个旋转方向相反的旋涡分别从圆柱的上下两侧脱落。Re＝60 000（U*water＝11．07）时，涡量场已经变得较为复杂，尾迹旋涡形态为2P+4S模式，其中P（Pair）表示一个旋涡对。Re＝90 000（U*water＝16．61）时，涡量场变得更加复杂，每个振动周期内有16个旋涡形成，尾涡形态变得极不稳定。

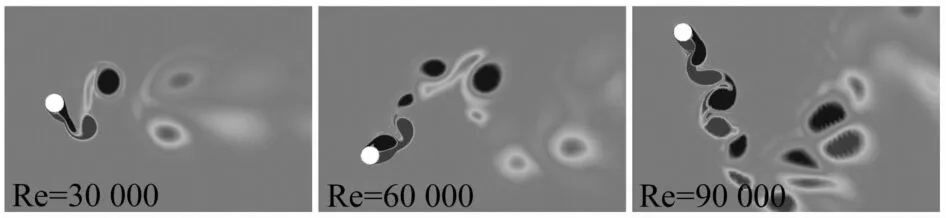
图6 粗糙表面圆柱尾迹旋涡形态Fig．6 Vortex structures of circular cylinder with rough surface

图7所示为不同Re时方柱尾迹旋涡形态。Re＝30 000（U*water＝5．79）时，方柱流致振动位于VIV初始分支，尾迹旋涡形态为典型的2S模式。Re＝60 000（U*water＝11．58）时，振动位于VIV上部分支，与VIV初始分支不同，尾涡形态已经转变为2P+2S模式。Re＝90 000（U*water＝17．36）时，振动位于VIV－驰振过渡阶段，涡量场已经变得比较复杂，尾涡形态为2P+4S模式。

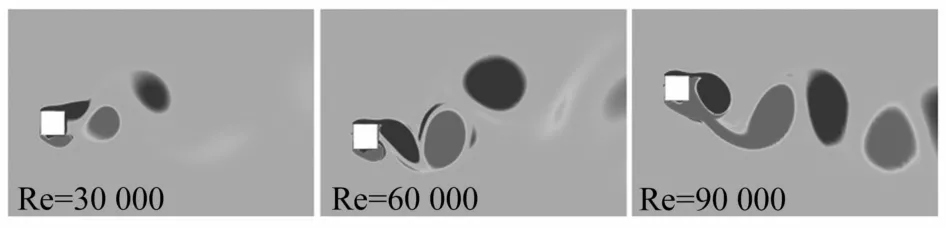
图7 方柱尾迹旋涡形态Fig．7 Vortex structures of square cylinder

图8所示为Re＝30 000／60 000／90 000时三角柱的尾迹旋涡形态。从图中可以看出，Re＝30 000（U*water＝5．09）时，三角柱流致振动位于VIV初始分支，尾迹旋涡形态与圆柱和方柱相比，已经发生明显变化，为2P模式。Re＝60 000（U*water＝10．19）时，振动位于VIV上部分支，与VIV初始分支不同，尾涡形态已经转变为2P +2S模式。Re＝90 000（U*water＝15．28）时，振动位于VIV－驰振过渡阶段，一个振动周期内有12个旋涡形成。

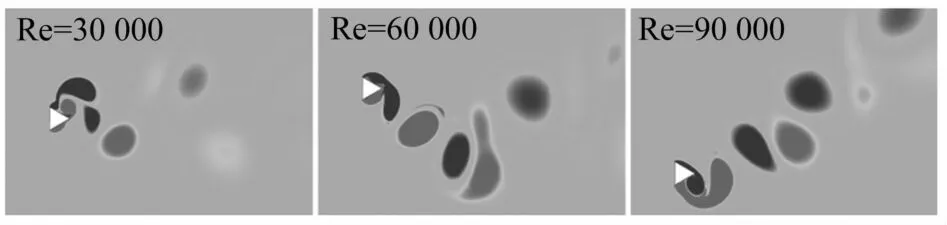
图8 三角柱尾迹旋涡形态Fig．8 Vortex structures of triangular prism

图9所示为类梯形柱Ⅰ的尾迹旋涡形态。在Re＝30 000（U*water＝5．57）时，类梯形柱Ⅰ在一个振动周期内出现4个脱体旋涡，与三角柱相同，为2P模式。随着Re增加，当Re＝60 000（U*water＝11．14）时，柱体处于VIV上部分支，振动稳定，尾迹旋涡形态为2P+4S，与圆柱的尾迹旋涡形态相同。当类梯形柱Ⅰ振动进入VIV－振动过渡区时，其旋涡脱落形态并不稳定，在一个周期内观察到4个旋涡对和多个单旋涡脱落。

图9 类梯形柱Ⅰ尾迹旋涡形态Fig．9 Vortex structures of quasi-trapezoid cylinderⅠ

由于类梯形柱Ⅱ的流致振动响应与圆柱、方柱、三角柱和类梯形柱Ⅰ完全不相同，其尾迹旋涡特征也不一样。在Re＝30 000／60 000／90 000（U*water＝5．57／11．14／16．7）这三个条件下时，尾迹旋涡形态全为2S模式，见图10。

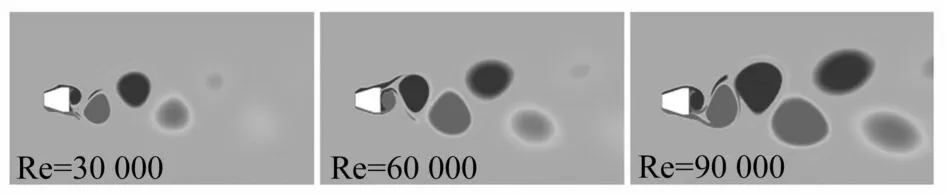
图10 类梯形柱Ⅱ尾迹旋涡形态Fig．10 Vortex structures of quasi-trapezoid cylinderⅡ

由以上分析可以看出，柱体流致振动振幅和频率与尾迹旋涡形态紧密相关，在不同的振动分支，尾迹呈现出不同的旋涡形态。当柱体流致振动处于某一分支时，其尾迹旋涡形态相对稳定；振动分支随雷诺数变化而发生切换时，尾涡形态也将由一种模态向另一种模态转变。由于柱体流致振动主要由升力驱动，升力的变化与柱体表面的边界层分离点密切相关，而脱体旋涡也是在边界层分离后形成和演变，因此边界层分离点位置就显得极为重要。方柱、三角柱和类梯形柱由于上下两侧棱边的存在，边界层分离点较为固定，在圆柱表面增加粗糙面后，其边界层分离也能得到预测。结合图4和图5中各种形状柱体的振幅和频率响应曲线可以看出，在相同来流速度时，粗糙表面圆柱和类梯形柱Ⅰ的流致振动响应均强于其他柱体，由于这两种柱体的边界层分离点位于柱体前端，柱体两侧边界层周期性分离后对柱体表面压力变化影响较大，从而导致柱体振幅高于其他柱体。虽然三角柱和方柱的边界层分离点也在柱体前部，但由于三角柱后部侧边陡度较大，使其升力变化受旋涡脱落影响较小，而方柱因为旋涡形成与演变均受后部棱角的影响，而且在后部棱角处会出现二次脱体旋涡的形成，影响方柱升力的周期性变化，因此，三角柱和方柱的振幅均低于圆柱和类梯形柱Ⅰ。另外，类梯形柱Ⅱ的边界层分离点靠近柱体尾部，由于在边界层分离点出现之前，柱体上下两侧流场和压力场相似，因此旋涡的交替脱落对柱体升力的影响较小，导致类梯形柱Ⅱ出现高频低幅的振动。

4 结 论

针对不同形状柱体流致振动问题进行数值分析，物理模型包括圆形、方形、三角形和类梯形截面形状。运用有限体积法，采用基于URANS的Spalart-Allmaras湍流模型，研究高雷诺数条件下（30 000≤Re≤110 000）柱体流致振动特性。详细分析了不同形状柱体振幅、频率和尾迹旋涡形态，探讨了各种因素对柱体后旋涡脱落的影响，将各个形状柱体流致振动的振幅和频率的变化规律进行对比。得出了以下结论：

（1）柱体截面形状对流致振动产生明显影响。由于粗糙表面圆柱和类梯形柱Ⅰ的边界层分离点位于柱体前端，并且边界层的交替分离对柱体受力影响较大，因此在相同Re数下，粗糙表面圆柱和类梯形柱Ⅰ的流致振动响应均强于其他形状柱体，最大振幅达到3．5D。

（2）圆柱、方柱、三角柱和类梯形柱Ⅰ的流致振动随来流速度变化均出现了几个不同的振动分支，分别是VIV初始分支、VIV上部分支、VIV－驰振过渡分支和驰振，而类梯形柱Ⅱ出现高频低幅振动，在所研究的整个Re范围内并未观察到明显的振动分支。

（3）柱体流致振动振幅和频率与尾迹旋涡形态紧密相关，在不同的振动分支，尾迹呈现出不同的旋涡形态。当柱体流致振动处于某一分支时，其尾迹旋涡形态相对稳定；振动分支随雷诺数变化而发生切换时，尾迹形态也将由一种模态向另一种模态转变。

［1］Williamson C H K，Govardhan R．Vortex-induced vibrations［J］．Annual Review of Fluid Mechanics，2004，36：413－455．

［2］唐世振，黄维平，刘建军，等．不同频率比时立管两向涡激振动及疲劳分析［J］．振动与冲击，2011，30（9）：124－128．

TANG Shi-zhen，HUANG Wei-ping，LIU Jian-jun，et al．Vortex induced vibration and fatigue damage of risers under two-dimensional vortex excitation considering different frequency ratios［J］．Journal of Vibration and Shock，2011，30（9）：124－128．

［3］孙雷，董晓磊，宗智，等．海洋立管两自由度振动的涡激损伤分析［J］．振动与冲击，2012，31（19）：99－103．

SUN Lei，DONG Xiao-lei，ZONG Zhi，et al．Analysis for VIV induced fatigue damage of a marine riser with 2－DOF［J］．Journal of Vibration and Shock，2012，31（19）：99－103．

［4］Bernitsas MM，Raghavan K，Ben-Simon Y，et al．VIVACE（vortex induced vibration aquatic clean energy）：A new concept in generation of clean and renewable energy from fluid flow［J］．Journal of Offshore Mechanics and Arctic Engineering-Transactions of the ASME，2008，130（4）：041101．

［5］Bearman PW．Circular cylinderwakes and vortex-induced vibrations［J］．Journal of Fluids and Structures，2011，27（5／6）：648－658．

［6］邓见，任安禄，邹建锋．方柱绕流横向驰振及涡致振动数值模拟［J］．浙江大学学报：工学版，2005，39（4）：595－599．

DENG Jian，REN An-lu，ZOU Jian-feng．Numerical study of transverse galloping and vortex-induced vibrations of square cylinder［J］．Journal of Zhejiang University：Engineering Science，2005，39（4）：595－599．

［7］Nemes A，Zhao J，Lo Jacono D，et al．The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack［J］．Journal of Fluid Mechanics，2012，710：102－130．

［8］Sheard G J，Fitzgerald MJ，Ryan K．Cylinders with square cross-section：wake instabilitieswith incidence angle variation［J］．Journal of Fluid Mechanics，2009，630：43－69．

［9］Kumar R A，Sohn CH，Gowda B L．Influence of corner radius on the near wake structure of a transversely oscillating square cylinder［J］．Journal ofMechanical Science and Technology，2009，23（9）：2390－2416．

［10］徐枫，欧进萍，肖仪清．不同截面形状柱体流致振动的CFD数值模拟［J］．工程力学，2009，26（4）：7－15．

XU Feng，OU Jin-ping，XIAO Yi-qing．CFD numerical simulation of flow-induced vibration with different cross-section cylinder［J］．Engineering Mechanics，2009，26（4）：7－15．

［11］Ding L，Bernitsas MM，Kim E S．2-D URANS vs．experiments of flow inducedmotions of two circular cylinders in tandem with passive turbulence control for30 000＜Re＜105 000［J］．Ocean Engineering，2013，72：429－440．

［12］Travin A，Shur M，Strelets M，et al．Detached-eddy simulations past a circular cylinder［J］．Flow Turbulence and Combustion，2000，63（1／4）：293－313．

［13］Chang C C．Hydrokinetic energy harnessing by enhancement of flow induced motion using passive turbulence control［D］．Ann Arbor，MI，USA：University of Michigan，2010．

Flow-induced motion of bluff bodies with different cross sections in flow field with high Reynolds number

DING Lin1，2，ZHANG Li2，JIANGDe-yi2
（1．Key Laboratory of Low-grade Energy Utilization Technologies and Systems（Chongqing University），Ministry of Education of China，Chongqing 400044，China；2．College of Resources and Environmental Science，Chongqing University，Chongqing 400044，China）

Flow-induced motion（FIM）is widely existing in the nature and engineering applications．The interactions between structure and flow are often very complex and the FIMis one of the research focuses in the fluidstructure interaction dynamics．In the present study，FIMof cylinderswith different cross sectionswas numerically studied in the flow field with high Reynolds number range of 30000≤Re≤110000．The amplitude，frequency，and vortex patterns of each cylinder were examined．The results indicate that the amplitudes of the circular cylinder with rough surface and the quasi-trapezoid cylinderⅠare higher than others，and themaximum amplitude of3．5 times of diameters is reached．The initial branch of VIV（vortex-induced vibration），the upper branch of VIV and galloping are correctly predicted in the oscillations of the circular cylinder，square cylinder，triangular prism，and quasi-trapezoid cylinderⅠ．FIMwith high frequency and small amplitude is achieved for the quasi-trapezoid cylinderⅡ，but no FIMbranch can be observed．In addition，the vortex pattern of cylinder is closely related with the amplitude and frequecy responses，and the vortex pattern is stable when the cylinder is in one branch．

flow-induced motion；vortex shedding；vortex-induced vibration；galloping

TK72

A

10．13465／j．cnki．jvs．2015．12．030

高等学校博士学科点优先发展领域专项科研基金（20120191130003）；国家自然科学基金（51406018）；重庆市博士后基金（XM2014091）

2014－03－14 修改稿收到日期：2014－06－03

丁林男，博士，讲师，1985年生

张力男，博士，教授，1956年生

邮箱：lizhang＠cqu．edu．cn