少齿差星轮型减速器的弹性动力学建模与模态分析

张 俊，郭 凡，谢胜龙

（安徽工业大学机械工程学院，安徽 马鞍山 243002）

少齿差星轮型减速器的弹性动力学建模与模态分析

张 俊，郭 凡，谢胜龙

（安徽工业大学机械工程学院，安徽 马鞍山 243002）

针对目前少齿差星轮型减速器在机械应用中行星轴承易烧毁的现象，对其进行力学分析以寻求解决的途径。基于子结构综合思想，将少齿差星轮型减速器划分为输出轴子系统、输入轴子系统、星轮轴子系统和平动星轮子系统，运用牛顿力学方法建立各子系统的运动微分方程。通过计入各轴承径向支承变形、齿轮副啮合变形以及输入轴和星轮轴上偏心套的分度误差和偏心误差等因素，构造系统各环节的变形协调条件，并将其与各子系统的运动微分方程结合，构建出少齿差星轮型减速器的弹性动力学方程。通过求解系统动力学方程的特征值问题，可获得其固有特性。以HJW－18B型星轮减速器为例，基于所建动力学模型对其进行了模态分析。结果表明，少齿差星轮型减速器的低阶固有频率远高于系统额定输入转频，一般不会引起结构谐振；系统低阶模态对应的振型表现为四类子系统的复合振动模式。在此基础上进一步进行了实验模态分析。对比发现，实验模态结果与理论仿真结果吻合较好，表明所建弹性动力学模型具有较高的计算精度，可准确揭示少齿差星轮型减速器的动态特性，从而为后续的受力分析、强度计算和结构优化提供准确的力学依据。

少齿差；星轮减速器；弹性动力学；变形协调条件；模态分析

少齿差行星齿轮传动的振动与噪声是影响其可靠性、使用寿命及操作环境的关键因素［1－2］。围绕该类传动的动力学问题，学术界开展了广泛研究，内容涉及动力学建模、固有特性分析、动态响应求解、振动和噪声抑制等多个方面。这其中，动力学建模与固有特性分析是进行后续动力学性能研究及减振降噪的理论基础。

按照建模时考虑因素和力学层次的不同，可将少齿差行星齿轮传动的动力学建模方法分为一般刚体力学方法、弹性静力学方法和弹性动力学方法。其中，一般刚体力学方法将机构中各构件视为刚体，利用静力平衡条件和力矩平衡条件建立系统的静力学方程。应海燕等［3-5］相继采用这种方法研究了三环减速器、双曲柄式精密行星传动和星轮减速器的受力问题，给出了系统关键零部件的载荷变化曲线。需要指出的是，因少齿差行星齿轮传动中存在虚约束，各构件不满足静定条件，故采用一般刚体力学方法无法准确求得各构件的受力。为此，在开展该类传动的力学分析时，必须计入尽可能多的影响因素，同时构造恰当的变形协调条件，方可建立能反映系统各环节真实受载状况的力学模型。宋轶民等［6］通过计入行星轴承和齿轮副的弹性变形，采用弹性静力学方法研究了三环减速器的受力和变形。类似地，张俊等［7］通过计入高速轴弯曲、环板拉压与弯曲、齿轮副、轴承、支承轴扭转等变形，采用力—位移混合法建立了环板式减速器的弹性准静态模型，并进一步分析了系统中各零部件的受力状况。赵自强等［8－9］在计入各运动副处接触变形的基础上，通过建立弹性静力学模型相继研究了一类内平动齿轮机构和星轮减速器的受力问题。弹性静力学模型虽能在一定程度上反映少齿差传动的受载状况，但却无法揭示系统的动态特性，如固有频率、振动模式等。为明晰传动系统的振动机理，必须建立相应的动力学模型。杨建明等［10－11］建立了三环减速器的弹性动力学模型，并依托该模型分析了系统的固有特性和稳态动响应。在此基础上，宋轶民等［12－13］进一步计入了环板和高速轴支承轴承的变形，建立了考虑更多影响因素的少齿差环板式减速器的动力学模型，相继分析了相位差120°的三环减速器和非对称180°相位差的新型双环减速器的动态特性。

相比其他型式的少齿差行星传动，星轮型减速器为实现功率分流而采用多根星轮轴均布的结构，导致系统中存在多重虚约束，也使得该类传动装置的动力学分析极具挑战性。迄今为止，尚未见到少齿差星轮型减速器动力学研究的文献。有鉴于此，本文将根据星轮型减速器的传动原理与结构特点，通过计入轴承和齿轮副的变形以及偏心套误差等因素，构造系统的变形协调条件，并结合动态子结构法，建立该类减速器的弹性动力学模型。在此基础上，进一步开展系统的模态分析，并将理论分析结果与实验模态结果进行对比，以验证所建弹性动力学模型的精确性。论文工作将为后续的动响应分析、参数灵敏度分析、误差影响分析、动态设计与性能优化提供理论依据。

1 弹性动力学建模

不失一般性，以内齿轮输出型星轮减速器为例（见图1），建立其弹性动力学模型，所用方法同样适用于其它型式的少齿差星轮型减速器。

为尽可能多地反映系统的动力学本质，同时避免数学处理上过于复杂，对实际系统作如下假设：

（1）因减速器中各轴的转速均低于1 500 r／min，远低于各轴自身的一阶临界转速，且由于星轮减速器结构紧凑，各轴均短而粗，因此将各轴视为刚体，只计入各轴上支承轴承的弹性变形；

（2）与其他变形环节相比，箱体的刚度较大，故忽略箱体轴承座处的变形；

（3）因支撑盘和各支承轴仅起支承作用，故忽略支撑盘和各支承轴的变形；

（4）计入齿轮副的啮合变形，且啮合刚度取内啮合齿轮副的时变啮合刚度；

（5）各星轮及其组件均相同，各星轮轴按理论角度呈周向均布，但计入各轴上偏心的制造、安装误差；

（6）因少齿差星轮型减速器一般采用渐开线直齿轮，其轴向载荷可忽略不计，故设定系统中两相平动星轮仅作平面运动，各轴不发生轴向窜动。

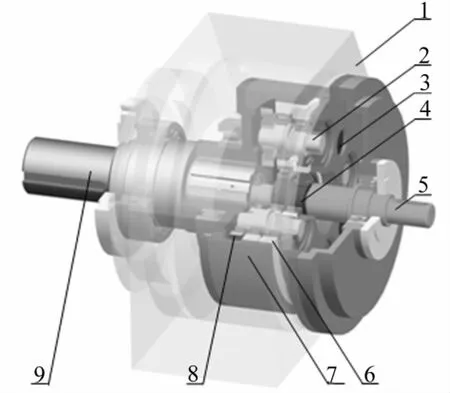
图1 内齿轮输出型星轮减速器结构图Fig．1 The structure of spider reducer with ring-gear-output type

为方便建模，采用动态子结构法，将整个齿轮传动系统划分为输出轴子系统、输入轴子系统、星轮轴子系统以及平动星轮子系统，分别建立各子系统的运动微分方程。不妨定义如下全局参考坐标系O-xyz：以内齿轮几何中心O为坐标原点，以重力加速度的反方向为y轴方向，z轴方向与输入轴轴线重合并指向输入端，x轴方向由右手定则确定。

1.1 输出轴子系统运动微分方程

输出轴子系统由内齿轮、法兰和输出轴组成。其中，内齿轮和法兰之间通过螺栓连接，法兰和输出轴之间通过花键连接，故可将三者视为一体，其受力情况见图2。

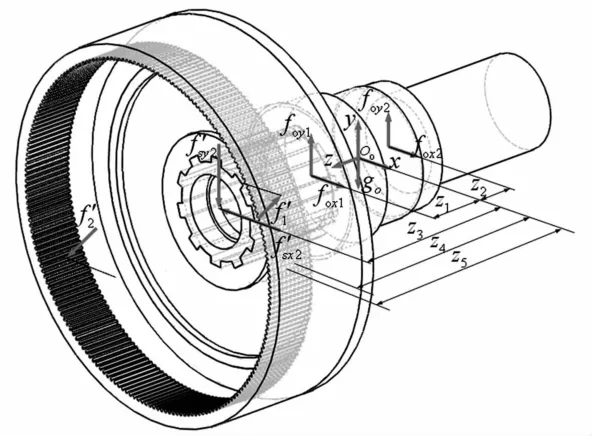
图2 输出轴子系统受力示意图Fig．2 Force diagram of the output shaft

图2中，Oo-xyz为输出轴质心处连体坐标系；z1、z2为输出轴质心至输出轴前、后端支承轴承支承点的距离；z3为输出轴质心至输入轴后端支承轴承支承点的距离；z4、z5为输出轴质心至第1、第2相机构齿轮副中点的距离；go为输出轴的重量；fox1、foy1，fox2、foy2分别为输出轴前、后端轴承在x，y方向的支反力；fsx2、fsy2为输入轴后端轴承x，y方向的支反力；f1′、f2′为内齿轮与第1、第2相平动星轮的啮合力。

通过分析，可建立输出轴子系统的运动微分方程

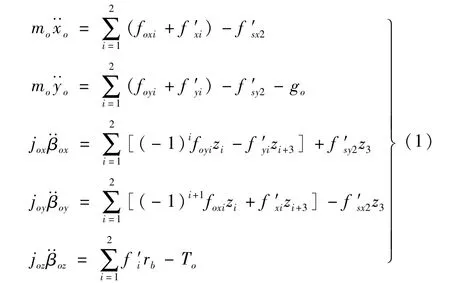
式中：mo，jox，joy，joz分别为输出轴的质量和绕x，y，z轴的转动惯量；f′xi，f′yi为啮合力fi′沿x方向和y方向的分量（i＝1，2，后同）；rb为内齿轮的基圆半径；xo，yo为输出轴子系统质心沿x，y方向的位移；βox，βoy，βoz为输出轴子系统绕x，y，z轴的角位移。

1.2 输入轴子系统运动微分方程

输入轴子系统由输入轴和其上的偏心套组成。由于输入轴和偏心套之间通过2个呈180°对称布置的键连接，故可将二者视为一体，其受力情况见图3。

图3中，OI-xyz为输入轴质心处连体坐标系；a1，a2为输入轴质心至前、后端支承轴承支承点的距离；a3，a4为输入轴质心至第1、第2相机构偏心套中点的距离；gI为输入轴的重量；fsx1，fsy1，fsx2，fsy2分别为输入轴前、后端轴承在x，y方向的支反力；fIxi，fIyi为第i相平动星轮上行星轴承在x，y方向的支反力；fexi，feyi为输入轴在第i相平动星轮处的离心力在x，y方向的分量。

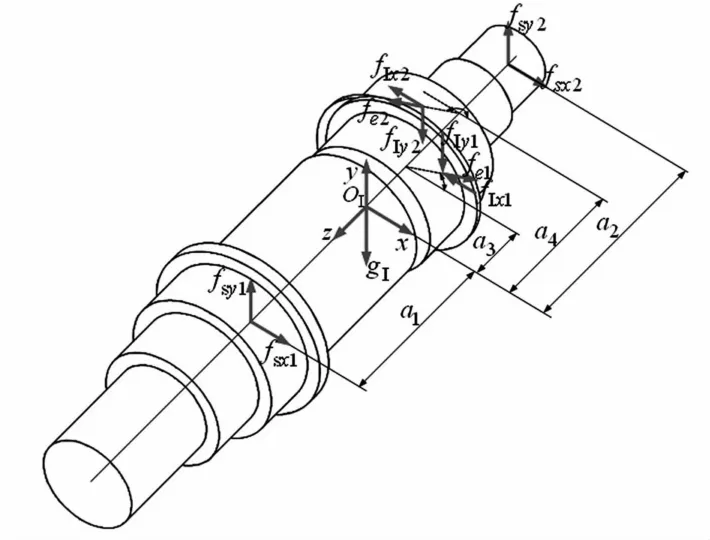
图3 输入轴子系统受力示意图Fig．3 Force diagram of the input shaft

类似地，可建立输入轴子系统的运动微分方程

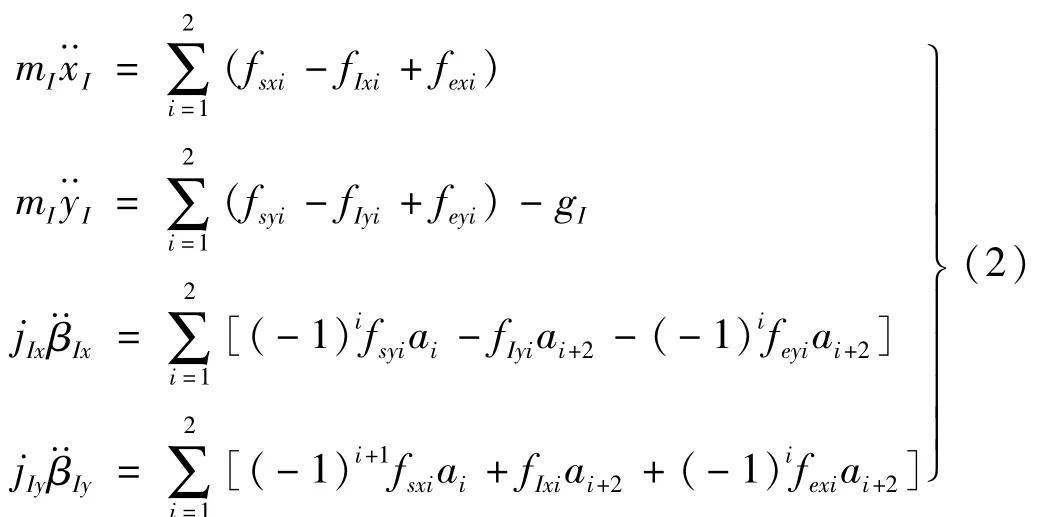
式中：mI，jIx，jIy为输入轴的质量和绕x，y轴的转动惯量及重量；xI、yI，βIx，βIy分别为输入轴子系统质心沿x，y方向的线位移及绕x，y轴的角位移。

1.3 星轮轴子系统运动微分方程

不失一般性，仅以第j根星轮轴为例，分析该子系统的受力，其受力情况如图4所示。

图4中，Os-xyz为星轮轴质心处连体坐标系；b1、b2为星轮轴质心至输入轴前、后端支承轴承支承点的距离；b3，b4为星轮轴质心至第1、第2相机构偏心套中点的距离；φ1，φ2分别为第1、第2相机构的曲柄转角；gsj为第j根星轮轴的重量；fhx1j，fhy1j，fhx2j，fhy2j分别为第j根星轮轴前、后端轴承在x，y方向的支反力；fsxij，fsyij为第i相平动星轮上行星轴承作用于第j根星轮轴上的支反力在x，y方向上的分量；fgxij，fgyij为第j根星轮轴在第i相平动星轮处的离心力在x，y方向上的分量。

由受力平衡可导出星轮轴子系统的运动微分方程

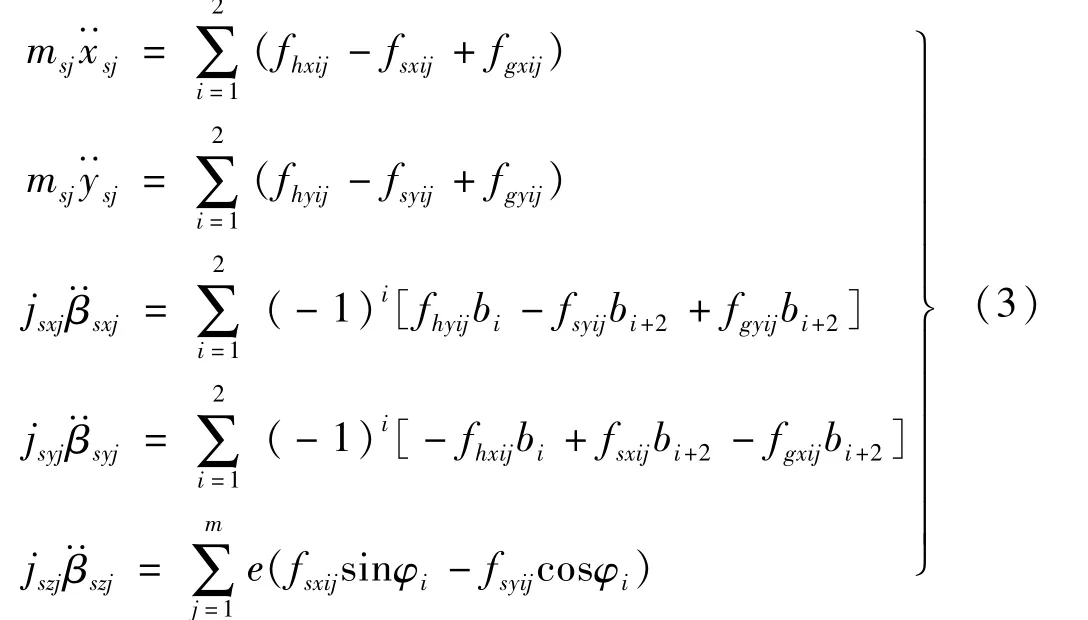
式中，下标i，j分别为机构相数和星轮轴的根数，且有i＝1，2，j＝1～m（m为星轮轴总根数）；msj，jsxj，jsyj，jszj为第j根星轮轴的质量和绕x，y，z轴的转动惯量；xsj，ysj为星轮轴子系统质心沿x，y轴方向的位移；βsxj，βsyj，βszj为星轮轴子系统绕x，y，z轴的角位移。

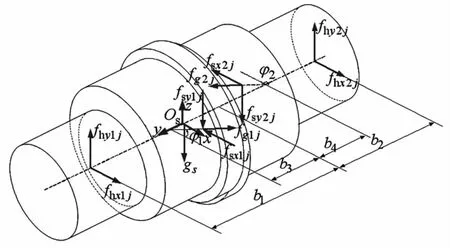
图4 第j根星轮轴受力示意图Fig．4 Force diagram of the jthspider shaft

1.4 平动星轮子系统运动微分方程

不失一般性，仅以第i相机构的平动星轮为例，分析该类子系统的受力，其受力情况见图5。

图5中，Oi为第i相平动星轮的理论几何中心；P为理论啮合节点；L为星轮上各星轮轴轴孔的分布半径；φj为第j根星轮轴的相位角；φi为第i相机构曲柄的转角；Ψi＝π／2－α′+φi，α′为啮合角；gpi为第i相平动星轮的重量；fpi为平动星轮的离心力；其他符号的含义同前。

不难导出星轮子系统的运动微分方程如下

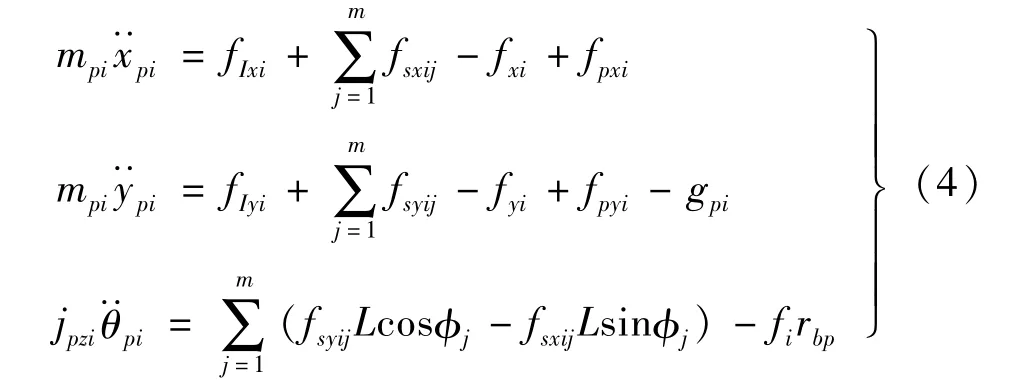
式中：xpi、ypi为第i相平动星轮的质心相对于其理论位置在x，y方向的位移；θpi为第i相平动星轮相对于其理论位置的转角；mpi、jpzi为第i相平动星轮的质量、及绕z轴的转动惯量；rbp为平动星轮的基圆半径。

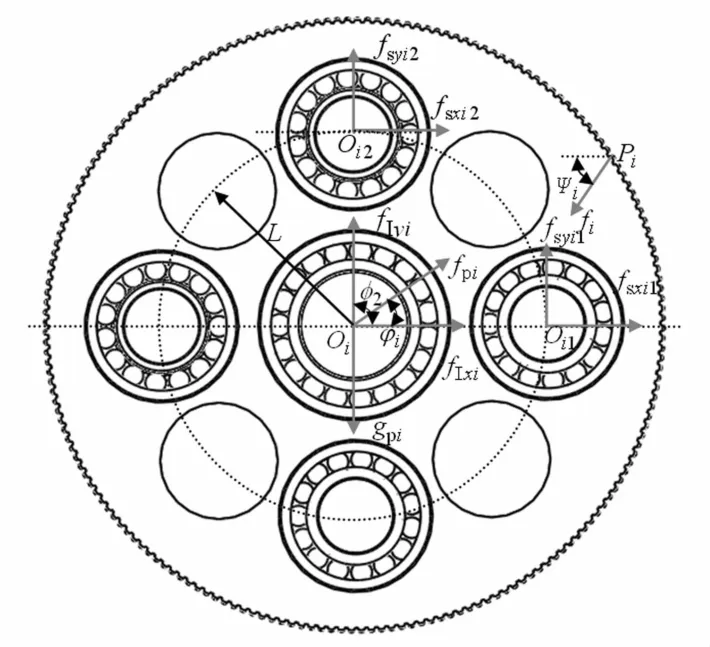
图5 第i个平动星轮受力示意图Fig．5 Force diagram of the ithspider gear

1.5 系统变形协调条件

（1）输入轴和星轮轴与平动星轮间位移关系

不失一般性，取第i相机构为研究对象，其弹性变形见图6。

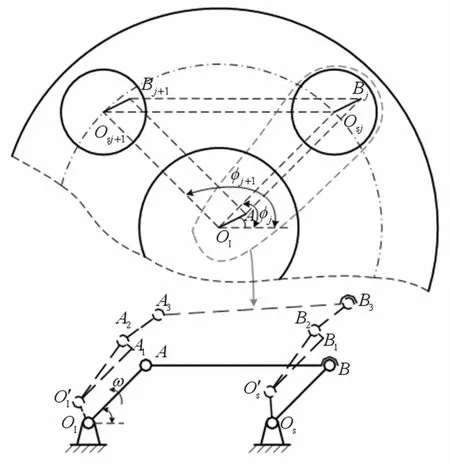
图6 输入轴和星轮轴处变形协调条件Fig．6 Deformations among input，spider shafts and spider gear

图6中，上半部分表示输入轴和m根星轮轴构成的平行四边形机构；下半部分中虚线表示机构变形后的实际位置，实线为没有弹性变形和误差的理论位置。其中，OIA为机构输入轴偏心套理论位置，OIO′I为输入轴在第i相机构处的位移，O′IA2为机构输入轴偏心套实际位置，O′IA1为偏心套的径向误差，A1A2为偏心套分度误差，A2A3为平动星轮的位移；OsB为机构星轮轴偏心套理论位置，OsO′s为星轮轴在第i相机构处的位移，O′s B2为机构星轮轴偏心套实际位置，O′sB1为偏心套的径向误差，B1B2为偏心套分度误差，B2B3为平动星轮的位移。

由图6可导出以下变形协调关系式。

（1）输入轴和平动星轮间变形协调关系式

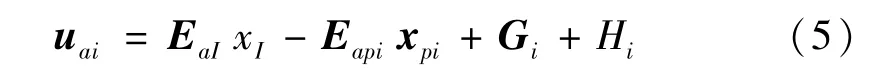
式中：uai为平动星轮上输入轴行星轴承孔的位移，xI为输入轴质心的位移向量，xpi为第i相平动星轮质心的位移向量，Gi、Hi分别为输入轴第i相偏心套的偏心误差和分度误差，EaI、Eapi为系数，且有

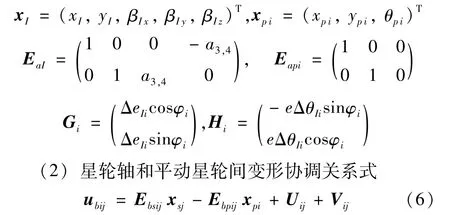
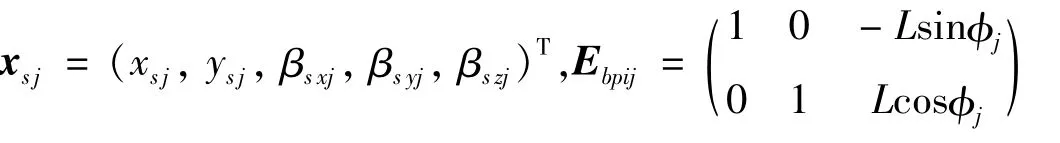
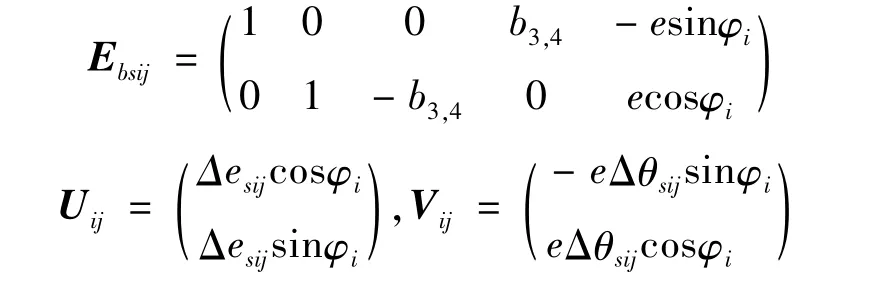
（2）齿轮副处变形协调关系

以第i相平动星轮与内齿轮的啮合为例，说明其变形协调条件，其位移关系见图7。

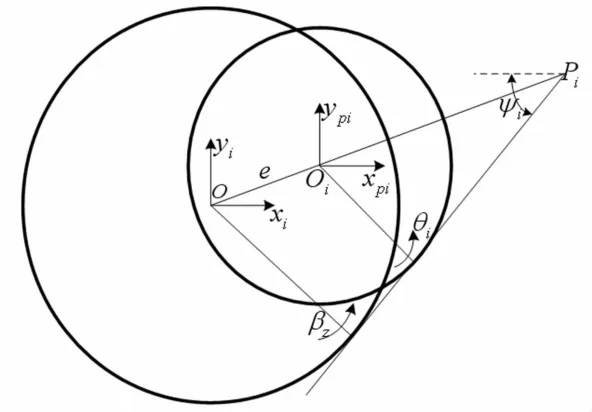
图7 平动星轮与内齿轮啮合位移示意图Fig．7 Deformations between spider gear and internal gear

根据图7所示位移关系，可得如下变形协调条件

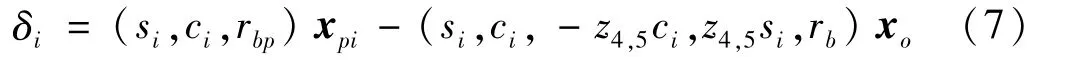
式中：δi为第i相机构内啮合副沿理论啮合线的相对位移；xo＝（xo，yo，βox，βoy，βoz）T为输出轴质心的位移向量。

将式（5）～式（7）表征的位移协调方程带入各子系统的运动微分方程，可得无阻尼情况下系统的弹性动力学方程如下

式中：m，k分别为组装后系统的质量矩阵和刚度矩阵，x，f分别为系统的广义位移列阵和外载荷列阵。各矩阵的表述形式如下：

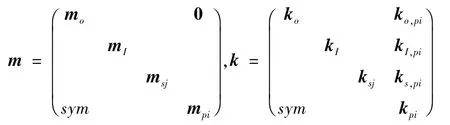
x＝（xo，xI，xsj，xpi）T，f＝（fo，fI，fsj，fpi）T。篇幅所限，相关子矩阵的具体元素不再详列。

2 固有特性分析与实验验证

式（8）中的广义特征值问题为

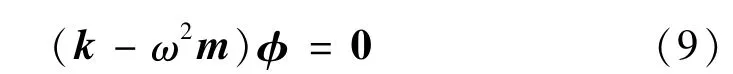
求解上述特征值问题，即可获得系统的模态特性。不失一般性，以江苏泰隆减速机股份有限公司的HJW－18B型星轮减速器为例，利用上述模型对其进行固有特性仿真分析。样机的基本参数为：外齿轮齿数z1＝192，内齿轮齿数z2＝196，齿轮副模数m＝1．5 mm，齿轮副啮合角α′＝25°；输入轴前、后端支承轴承刚度kI1、kI2分别为10 MN／m和20 MN／m；输入轴行星轴承刚度ka＝30 MN／m，输出轴前、后端支承轴承刚度ko1、ko2分别为30 MN／m和40 MN／m；星轮轴前、后端支承刚度ks1、ks2均为30 MN／m；星轮轴行星轴承刚度kp1、kp2均为30 MN／m；齿轮副平均综合啮合刚度km为300 MN／m。

由式（9）不难计算出一个运动周期内各离散位置处减速器的固有频率。限于篇幅，仅给出φ1＝0°时，系统前9阶固有频率及对应的振型描述，其结果见表1。

表1 基于理论模型的系统低阶模态特性Tab.1 The theoreticalmodal properties of lower orders of spider reducer

由表1可知，系统低阶固有频率的变化范围不大，前9阶固有频率的波动区间为［66．2，272．6］Hz。从数值上判断，结构尺寸近似的情况下，星轮型减速器的首阶固有频率值和波动幅值均小于三环减速器的频率值。究其原因，可能是星轮减速器属于内平动齿轮机构，其行星轴承的安装尺寸受星轮尺寸的制约，导致其支承刚度低于外平动齿轮构型的三环减速器，从而造成系统低阶固有频率值偏低。尽管如此，系统首阶固有频率值为66．2 Hz，依然远高于减速器的输入转频（25 Hz，额定转速1 500 r／min），故其输入转频一般不会引起减速器的结构共振。另一方面，从表中可以看出，与星轮减速器低阶固有频率对应的模态振型一般表现为各子系统的复合振动模式，区别仅在于各阶振型中某一类子系统的振动模式占主导地位。

同时，为直观起见，图8示出了系统低阶固有频率对应的模态能量分布。图中，各下标的含义为：O表示输出轴子系统；I表示输入轴子系统；S1，S2，S3和S4分别表示4根星轮轴子系统；P1和P2分别表示2个平动星轮子系统。为清晰计，各子系统的模态能量均作归一化处理。

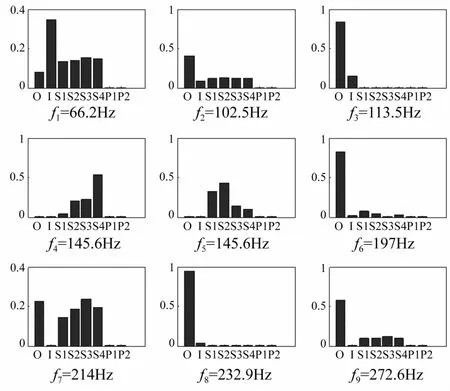
图8 系统各子系统前9阶模态能量图Fig．8 Themodal energy of the first9 orders of each subsystem

为验证上述少齿差星轮型减速器弹性动力学模型的计算精度，利用锤击法进行了该样机的试验模态分析，其实验原理和现场照片分别见图9、图10。

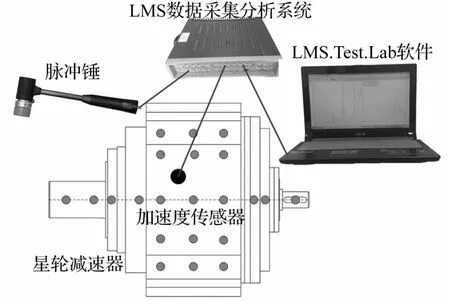
图9 实验原理图Fig．9 The schematic diagram experimental test

图11为经由LMS Test．Lab数据处理后的频响函数。虚线为输入信号x方向的频响函数曲线，实线为输出信号x方向的频响函数曲线。

将上述实验模态结果与前文的理论计算结果列表对比，以验证本文所建理论模型的正确性。相关对比数据见表2。

图10 实验现场照片Fig．10 The photo of experimental scene

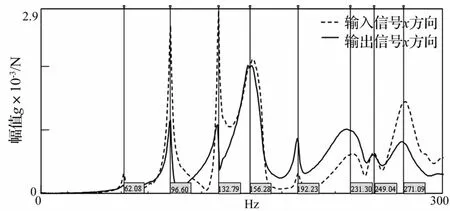
图11 星轮减速器频响函数曲线Fig．11 The frequency response function curve of Spider Reducer

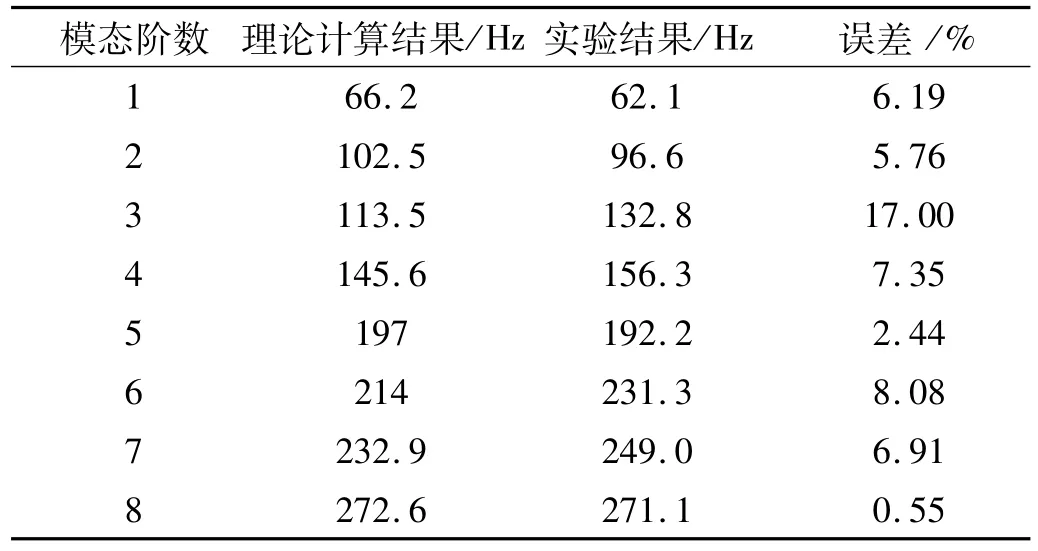
表2 理论与实验模态分析结果对比Tab.2 Com parison of theoretical and experimental results

从表2可知，就系统低阶固有频率而言，基于弹性动力学模型的理论分析结果与实验模态测试的固有频率结果在数值上均较为接近，部分阶次的固有频率甚至几乎相同。虽然系统第3阶固有频率的误差较大，但结合表1的振型描述可知，系统第3阶模态振型主要表现为输出轴的摆动，因输出轴为悬臂式结构，且输入轴后端通过支承轴承安装于空心结构的输出轴前端，当输出轴摆动时必然引起输入轴的附加振动。进一步分析可知，系统低阶固有频率对输入轴支承轴承的刚度变化较为敏感，故如果输入轴与输出轴耦合处的支承轴承安装导致其与理论估算刚度值有出入，则在系统层面将引起较大的计算误差。表2中所示的17%计算误差很可能由此产生。故总体而言，可以认为理论分析结果与模态实验的实测结果吻合较好，从而也表明了本文所建的弹性动力学模型具有较高的计算精度，可用于后续的动力学分析及参数优化设计。

3 结 论

（1）少齿差星轮型减速器的低阶固有频率远高于系统的输入转频，一般不会产生因输入激起的结构共振；

（2）少齿差星轮型减速器的低阶固有频率值比较密集，且系统出现重根，这与其多星轮轴的复杂结构及多重约束的结构对称性有关。

（3）少齿差星轮型减速器的低阶模态振型较为复杂，一般表现为各个子系统的复合振动模式，区别仅在于各阶振型中某一类子系统的振动模式占主导地位。

（4）基于弹性动力学模型的理论分析结果与实验模态的测试结果吻合较好，表明本文建立的少齿差星轮型减速器弹性动力学方程具有较高的精度，可作为后续动态特性分析和优化设计的基础模型。

［1］刘文，林腾蛟，李润方，等．新型少齿差减速器动态特性分析及实验研究［J］．振动与冲击，2009，28（7）：22－27．

LIU Wen，LIN Teng-jiao，LI Run-fang，et al．Dynamic characteristic analysis and experimental research of a new type reducer with small tooth number difference［J］．Journal of Vibration and Shock，2009，28（7）：22－27．

［2］石万凯，刘敬，龚建春．同轴对转行星齿轮传动系统动态特性分析［J］．振动与冲击，2014，33（7）：99－104．

SHIWan-kai，LIU Jing，GONG Jian-chun．Dynamic characteristics analysis for a co-axial counter-rotating planetary gear transmission system［J］．Journal of Vibration and Shock，2014，33（7）：99－104．

［3］应海燕，杨锡和．K－H型三环减速器的研究［J］．机械传动，1992，16（4）：37－43．

YING Hai-yan，YANG Xi-he．Research of three-ring reducer of K-H type［J］．Journal of Mechanical Transmission，1992，16（4）：37－43．

［4］王光建，蒋汉军，褚志刚．新型双曲柄式可调侧隙精密行星传动装置参数设计与仿真［J］．机械工程学报，2011，47（5）：11－18．

WANG Guang-jian，JIANG Han-jun，CHU Zhi-gang．Parameters design and simulation of new double crank adjustable backlash precision planetary gears［J］．Journal ofMechanical Engineering，2011，47（5）：11－18．

［5］李传兵．混合少齿差星轮减速器星轮轴承寿命计算［J］．安徽工业大学学报，2005，22（2）：156－158．

LIChuan-bing．Life calculation of planetary wheel bearing of speed reducer with complexminor tooth difference［J］．Journal ofAnhui University of Technology，2005，22（2）：156－158．

［6］宋轶民，张俊，郑奇斌，等．双环减速器的弹性动态静力分析［J］．农业机械学报，2007，38（10）：122－126．

SONG Yi-min，ZHANG jun，ZHENG Qi-bing，et al．Elastoquasi-static analysis of double-ring gear reducer［J］．Transactions of the Chinese Society for Agricultural Machinery，2007，38（10）：122－126．

［7］张俊，宋轶民，郑奇斌．环板式减速器的弹性准静态受力分析［J］．中国机械工程，2009，20（13）：1594－1599．

ZHANG Jun，SONG Yi-min，ZHENG Qi-bin．Elasto-quasistatic analysis ofmulti-ring gear reducers［J］．China Mechanical Engineering，2009，20（13）：1594－1599．

［8］赵自强，张春林，程爱明，等．有多重虚约束的内平动齿轮传动机构力学分析［J］．北京理工大学学报，2008，28（9）：768－772．

ZHAO Zi-qiang，ZHANG Chun-lin，CHENG Ai-ming，et al．Force analysis on internal parallelmove geartransmission with multiple redundant constrains［J］．Journal of Beijing Institute of Technology，2008，28（9）：768－772．

［9］张俊，谢胜龙，徐培民，等．少齿差星轮型减速器的弹性静力学分析［J］．农业工程学报，2013，29（24）：49－55．

ZHANG Jun，XIE Sheng-long，XU Pei-min，et al．Elastostatics analysis of spider reducer with small tooth number difference［J］．Transactions of the Chinese Society of Agricultural Engineering，2013，29（24）：49－55．

［10］杨建明．三环传动弹性动力学的理论与实验研究［D］．天津：天津大学，2001．

［11］Yang Jian-ming，Zhang Ce．Elasto-dynamics of internal gear planetary transmissions［J］．Mechanism and Machine Theory，2005，40：1107－1125．

［12］宋轶民，张俊，张永新，等．计入内齿板变形的环式减速器弹性动力分析［J］．机械工程学报，2006，42（9）：29－32．

SONG Yi-min，ZHANG Jun，ZHANG Yong-xin，et al．Elasto-dynamic Analysis ofmulti-ring gear reducers in consideration of deformations of gear-couplers［J］．Chinese Journal of Mechanical Engineering，2006，42（9）：29－32．

［13］张俊，宋轶民，张策．少齿差环板式减速器的弹性动力学分析［J］．机械工程学报，2008，44（2）：118－128．

ZHANG Jun，SONG Yi-min，ZHANG Ce．Elasto-dynamic analysis of ring-plate gear reducer with small tooth number difference［J］．Chinese Journal of Mechanical Engineering，2008，44（2）：118－128．

Elasto-dynam icmodeling and modal analysis of spider reducer with small tooth number difference

ZHANG Jun，GUO Fan，XIE Sheng-long
（School of Mechanical Engineering，Anhui University of Technology，Ma'an'shan 243032，China）

In order to solve the problems of teeth breakage and premature fatigue of planetary bearings in spider reducers，a methodology of dynamic modeling for spider reducers was proposed and its dynamic characteristics were analyzed．With the substructure synthesis technique，a lumped parameter elasto-dynamicmodel of the spider reducer was established．The transmission system was divided into four subsystems as the input shaft subsystem，output shaft subsystem，spider shaft subsystem and translational spider gear subsystem．The differentialmotion equations of the four subsystemswere derived by using the Newtonian method．The compatibility conditions of the reducer were derived with considering the deflections of bearings and gear pairs and the index and eccentric errors of eccentric sleeves．By combining the compatibility conditions with subsystem motion equations，the governing motion equations of the reducer were formulated．Through the eigenvalue decomposition，themodal properties of the transmission system were analyzed and the lower orders of natural frequencies and corresponding vibration modes were classified．The results show that the lower orders of natural frequencies are far above the rated input rotation frequency of the reducer，so it is not possible to cause structural resonances．Meanwhile，the corresponding vibrationmodes behave as complicated compound vibrationmodes of the four subsystems．To verify the correctness of theoretical analysis，an impact modal test was carried out．The comparison of lower orders of natural frequencies reveals a good match between theoretical and experimental results．From this point of view，it can be concluded that the proposed elasto-dynamicmodel si of satisfactory accuracy，and hence can be used to predict the steady-state dynamic responses of the system．The present research provides a solid fundament for further dynamic design and structural optimization of spider reducers．

small tooth number difference；spider reducer；elasto-dynamics；deformation compatibility condition；modal analysis

TH132．4

A

10．13465／j．cnki．jvs．2015．12．029

国家自然科学基金（51375013，50905122）；安徽省自然科学基金（1208085ME64）

2014－05－10 修改稿收到日期：2014－06－17

张俊 男，博士，教授，硕士生导师，1981年生