温度效应对铁路钢桥行车性能影响研究

田 园，张 楠，孙 奇，杜宪亭，夏 禾

（北京交通大学土木建筑工程学院，北京 100044）

温度效应对铁路钢桥行车性能影响研究

田 园，张 楠，孙 奇，杜宪亭，夏 禾

（北京交通大学土木建筑工程学院，北京 100044）

日照作用所引起的温度效应使得铁路桥梁产生明显变形，进而影响行车安全性。为研究此问题，首先借助于ANSYS有限元软件的热－应力耦合技术进行桥梁温度场和位移场分析，以获得日照作用下的轨道变形。其中，桥梁热分析边界条件由热辐射、热对流、热传导等太阳物理学综合因素及相关经验公式确定；采用构件截面切分简化分析模型。然后，建立车桥耦合振动分析模型，将温度效应引起的梁体变形和轨道不平顺叠加效应作为系统激励，采用全过程迭代法求解系统响应。最后，以某铁路简支钢板梁桥为例进行车－桥动力计算，结果表明：日照作用下列车通过桥梁时，桥梁的加速度没有明显差异，但横向和竖向位移均有所增加，同时桥上行车安全性和舒适性均有所降低。

车桥耦合振动；温度效应；热分析；行车安全性；铁路钢桥

近年来铁路建设发展迅猛，以桥代路的修建方式使桥梁比重大大增加。长大桥梁结构长期处于露天环境中，受到日照和环境温度作用。一方面，温度效应引起结构应力场发生变化，可能造成应力集中、局部破坏，甚至是整体失效；另外一方面，温度效应引起结构位移场改变，可能与既有轨道不平顺相叠加，增大系统激励从而降低结构行车性能。

针对桥梁结构的温度场，国内外学者已取得大量显著成果［1］。在理论研究方面，Zuk［2］发现高速公路箱梁桥结构的温度效应与材料性能、空气温度和太阳辐射等因素有关。Kehlbeck［3］提出了桥梁结构温度场分析的基本方法，建立了求解材料内部热传导问题的边界条件模型并进行了数值分析。美国AASHTO等［4］规范鉴于相关研究，均增加温度效应内容以进行修正。Tong等［5］考虑了钢桥截面的温度分布情况。刘兴法等［6－9］分别针对混凝土结构、钢－混凝土叠合梁结构和钢管混凝土结构优化了常规温度梯度和应力的认识。在实测试验研究方面，Wang等［10－11］考虑了结构响应及动力特性与温度的关系。Xia等［12－13］通过试验探究了日照太阳辐射特点及温度分布问题。

不难看出，上述研究均止步于温度效应引起的应力分析，属于静力分析的范畴。而温度效应可能引起的行车性能降低问题属于动力分析的范畴，鲜见其相关研究。

为此，本文提出了温度效应对铁路桥梁行车性能影响的分析框架。首先，借助于ANSYS有限元软件的热－应力耦合技术进行桥梁温度场和位移场分析，以获得日照作用下的轨道变形。其中，桥梁热分析边界条件由热辐射、热对流、热传导等太阳物理学综合因素及相关经验公式确定；采用构件截面切分并结合遮挡系数简化分析模型。然后，建立车桥耦合振动分析模型，将温度效应引起的梁体变形和轨道不平顺叠加作为系统激励，采用全过程迭代法求解系统响应。最后，以某典型铁路简支钢板梁桥为例进行计算。

1 温度效应引起的桥梁位移场分析

桥梁在日照作用下的温度效应，包括温度场和位移场分析，其实质是求解针对特定的初始条件和边界条件的热传导微分方程。本文实例部分采用日出时刻桥梁温度作为初始条件，由于钢材比热容较小，此时桥梁已与空气温度趋于相同。为突出温度效应影响，假设桥梁纵向恰沿南北方向，腹板分别正对东西方向。

边界条件的建立依据桥梁与环境的热交换方式以及环境影响因素。既往研究表明，从日照全过程及确定控制温度荷载角度，只需分析使结构发生最不利温度荷载的极值情况，即多为晴朗、风速较小且温度变化较大的气象条件。本文采用常见瞬态热分析第二类边界条件，考虑太阳辐射、辐射热交换和对流热交换等方式（见图1）以及空气温度和风速等影响因素，以综合热流密度作用于桥梁结构表面。具体相关内容及计算详见参考文献［14－15］。

图1 日照下桥梁热交换示意图Fig．1 Diagram of heat exchange of bridge under sunshine

1.1 边界条件简化分析

结构任一表面与外界均存在对流热交换，两者的温度差异以及日照和风速的不同，使得各表面对流热交换系数hc不同，以致难以精确计算其综合热流密度。为简化计算且满足精度需要，根据钢板梁桥表面温度分布特点及其所需施加的边界条件类型，将表面分为若干部分，取各部分温度的平均值来计算该表面综合热流密度。

桥梁各构件之间存在着复杂的时变遮挡关系，数值模拟该过程非常复杂。鉴于所研究的明桥面钢板简支梁桥，其轨道铺设于轨枕上，轨枕架设在上翼缘板上，因此上翼缘板对轨道变形所占权重最大。对于两主梁间相互遮挡作用，根据所选定的时间步及相应时刻的太阳高度角，对主梁内侧表面作切分处理并编号，分别计算各切分表面日照全过程的综合热流密度。图2给出不同时刻的太阳射线方向以及相应截面编号。

图2 不同时刻太阳射线方向Fig．2 Directions of solar radiation at different times

上横梁和上纵联遮挡主梁内侧的太阳直射和散射，下横梁和下纵联遮挡其地面反射和地面辐射。基于钢板很薄且传热速度较快的假设，本文将遮挡的局部效应综合考虑为总能量的减少。令遮挡后表面接收的总能量与无遮挡表面接收的总能量之比作为遮挡系数。因此，对于同类表面，受遮挡部分与无遮挡部分可以施加经遮挡系数修正后的相同边界条件，详细取值见表1。

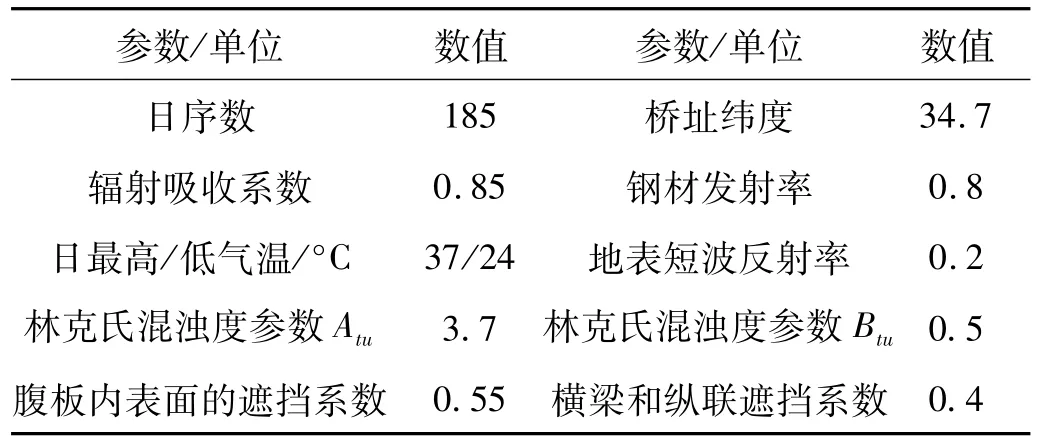
表1 钢桥热传导计算主要参数Tab.1 Main parameters of heat transfer calculation forthe steel bridge

此外，上横梁和上纵联在梁体上部，只有其外表面会受到太阳照射，而内表面不会；纵联、下纵联和下横梁在梁体下部，只有外表面会受到地面反射和辐射，而内表面不会。同样基于上文假设，将同一构件不同表面所受能量平均分配到该构件各个表面，以简化边界条件加载。

1.2 边界条件计算

计算得日出真太阳时（tr＝4：56）和日没真太阳时（ts＝19：12），取5∶00～19∶00为日照的全过程，以3°C为温度间隔，6 min为时间间隔，计算各个表面的综合热流密度。热传导计算相应参数见表1。

（2）为了促进信息传播，加强学术交流，在论文发表后，本刊享有文章的转摘权（包括英文版、电子版、网络版）。作者获得的稿费包括转摘酬金。如作者不同意转摘，请在投稿时说明。

部分时刻关键表面的综合热流密度计算结果列于表2，从表2可知：

（1）结构表面温度越高，综合热流密度越低。这是由于表面温度提高时，结构对外辐射量会变大，散失更多热量，导致综合热流密度降低；由于地面会吸收部分能量，所以顶表面的综合热流密度普遍高于底表面。

（2）东侧腹板外侧表面综合热流密度在9∶00达到最大值，而西侧腹板外侧表面综合热流密度在15∶00达到最大值。且西侧腹板外表面综合热流密度最大值比东侧腹板外表面大，因为下午的空气温度比上午的高，使得下午结构表面的综合热流密度较大。

（3）东侧腹板内表面在上午时属于背阳侧，下午部分时间可受到太阳直射，部分时间被西侧腹板遮挡，西侧反之。在受太阳直射与被遮挡的交替过程中，可以看到结构相应位置表面的综合热流密度变化较快，且部分表面会出现受太阳直射与被遮挡的交替过程中该值不是递变的情况。

1.3 基于ANSYS的热分析计算

在ANSYS中进行桥梁的热分析计算时，结构被离散成若干单元，根据能量守恒原理，利用初始条件和边界条件，对目标区域节点的热平衡方程进行求解，由此计算出全部节点的温度值。本文根据上述所计算综合热流密度的条件设定时间步和荷载值，并将数据写入文件以数组形式读入ANSYS完成日照过程中温度场计算。然后将温度场计算结果作为外荷载重新作用在桥梁模型上进行结构的温度效应分析，从而得到结构应力场和位移场响应。

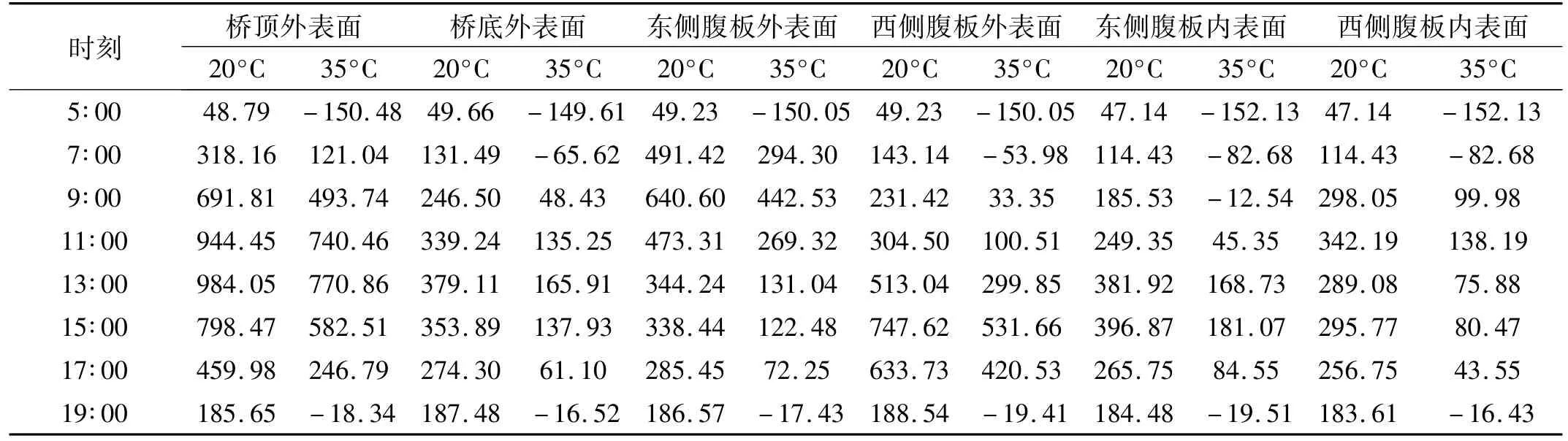
表2 不同时刻各表面综合热流密度Tab.2 Heat flux density of various surfaces at different times

2 车桥耦合振动分析模型

车桥动力相互作用分析采用的系统模型由列车子系统和桥梁子系统组成［16－17］，列车子系统依据多刚体动力学建立，桥梁子系统通过有限元建模。两系统之间通过轮对自由度相联系。轮轨作用力采用竖向轮轨密贴假定、横向线性简化的Kalker蠕滑理论，本文中轮对位移为温度效应下梁体位移和轨道不平顺的叠加。车桥系统耦合振动方程如下：

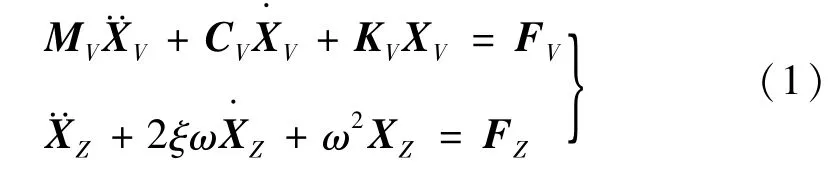
式中：MV、CV、KV、XV、FV为列车子系统的总体质量、阻尼、刚度、位移和作用力矩阵。XZ、ω、ξ、FZ为桥梁子系统的广义位移、圆频率、阻尼和广义力矩阵［18］。

式（1）为时变系数的二阶线性微分方程组，本文采用全过程迭代法求解系统响应。该方法假定桥梁子系统初始位移为零，利用轨道不平顺计算轮对运动状态，从而得到车辆运动状态及轮轨力时程，然后将所得轮轨力时程施加在桥梁模型上，独立求解桥梁方程，得到桥梁的运动状态时程，即完成一次迭代。在下一次迭代中，以桥面响应时程与轨道不平顺叠加作为新的车辆系统激励，以轮轨力是否收敛作为结束迭代的条件。其分析的流程见图3。

3 实例分析

本文以某铁路简支钢板梁桥为例，首先应用ANSYS软件建立该桥三维有限元模型，通过热－应力耦合技术对其进行温度场和位移场计算。然后，建立车桥耦合振动分析模型，将温度效应引起的梁体变形和轨道不平顺叠加效应作为系统激励，采用全过程迭代法求解系统响应。

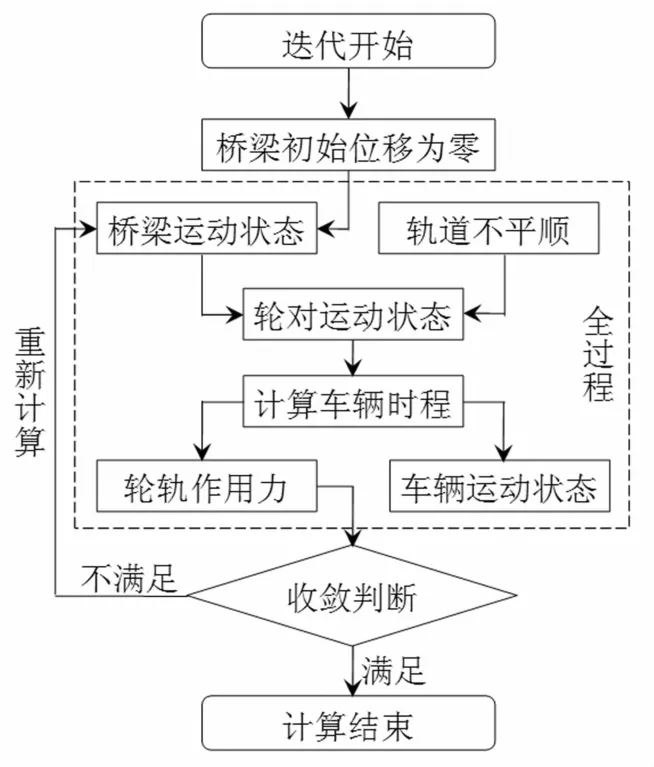
图3 全过程计算流程图Fig．3 Flow chart of the whole process of calculation

3.1 有限元模型的建立

选取10m×40m单线明桥面简支钢板梁桥为研究对象。该桥桁高3．232m，两主桁中心距为2．072m，节间长度为2 m。单线铁路布置于钢梁的上弦，密布纵横梁体系，桥梁标准横断面见图4。采用SOLID70单元建模，一跨模型由1 979 575个单元、661 606个节点组成，有限元模型见图5。全桥热分析计算材料参数见表3。

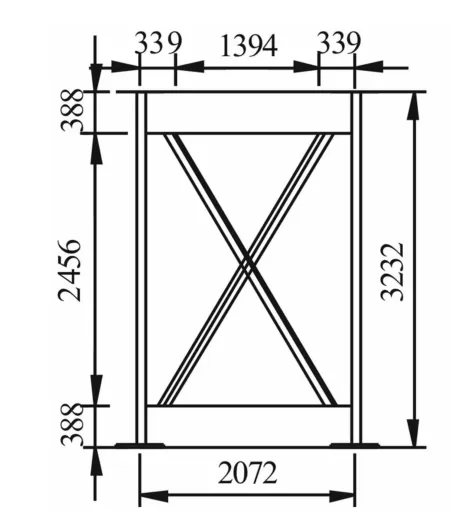
图4 桥梁标准横断面（单位：mm）Fig．4 Standard cross-section of bridge（unit：mm）

图5 简支梁钢板梁桥有限元模型Fig．5 Finite elementmethod model of the simply-supported steel plate girder bridge

表3 有限元模型基本参数Tab.3 Main parameters of finite elementmethod model

3.2 温度场和位移场计算

桥梁结构的温度场随时间不断变化，分析结果包括不同时刻结构整体的温度分布以及不同节点的温度日变化过程。图6给出了代表性时刻的桥梁温度分布图。

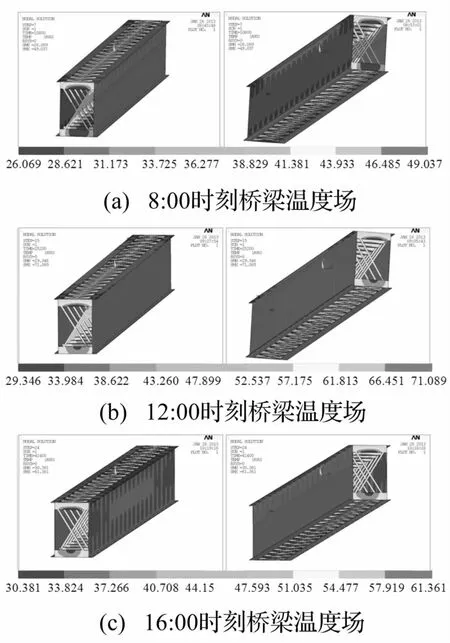
图6 不同时刻桥梁温度场Fig．6 Temperature fields of bridge at different times

图6表明，计算结果符合日照全过程中结构的温度变化规律，即桥梁结构首先在东侧升温（如图6（a）右图所示），然后转移至顶部，最后在西侧出现最高温度。由图6（b）可见，该时刻顶部与底部的温差已超过40°C；由图6（c）可见，该时刻东西两侧腹板的温差也已超过30°C。所以，有必要研究温度变化产生的温度效应使轨道发生变形，以及该变形对轨上列车走行安全性的影响。

温度效应分析结果包括不同时刻结构整体的变形场及应力场，以及局部的位移和应力变化过程。根据本文主要研究问题－车桥系统耦合振动问题，故重点关注结构变形。利用轨道处桥梁节点的位移代替轨道的位移，通过跨中轨道位置点与梁端轨道位置点的位移差确定行车最不利时刻。图7为东侧轨道跨中位置节点在温度效应下的时变位移图。图7表明温度效应使轨道产生明显变形，在8∶30和16∶30时刻，轨道横向和竖向相对位移的绝对值均较大（其中16∶30时刻最大），因此本文选择16∶30时刻位移场作为车桥外荷载激励出现的最不利时刻，同时列表给出8∶30时刻的车桥系统响应值作为比照。图8为16∶30时刻由温度引起的轨道竖向及横向变形曲线图。

3.3 车桥系统响应及分析

采用德国ICE－3列车，每节车长为24．775 m，动车轴重为160 kN，拖车轴重为146 kN，编组方式为6节动车+2节拖车。

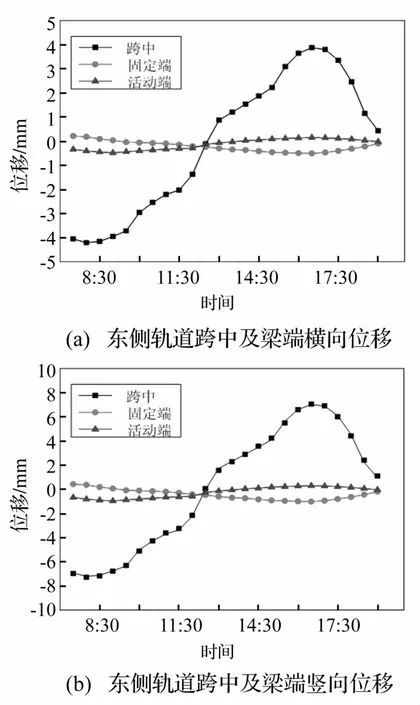
图7 东侧轨道跨中及梁端时变位移Fig．7 Time-varying displacements of the rail atmid-span on east side and beam end

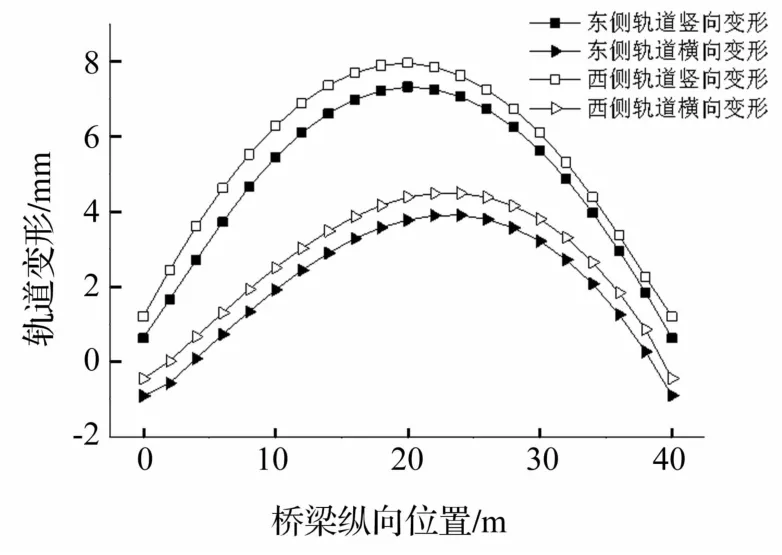
图8 16∶30时刻由温度引起的轨道竖向及横向变形曲线Fig．8 Lateral and vertical deformation of railinduced by temperature effect at16∶30

轨道不平顺参数采用德国低干扰谱转换的时域样本，所含波长范围为1～80m。其最大幅值为水平11．6 mm、高低7．3 mm、扭转6．68 mm／2．5 m。将温度效应引起的梁体变形和数值模拟的轨道不平顺叠加作为系统激励。

桥梁结构阻尼比取为0．01，积分时间步长取为0．001 s。取上文所确定的16∶30时刻作为桥梁结构变形的最不利时刻，列车以160 km／h的速度从北侧上桥，模拟列车过桥全过程，计算得到桥梁结构和列车的动力响应。

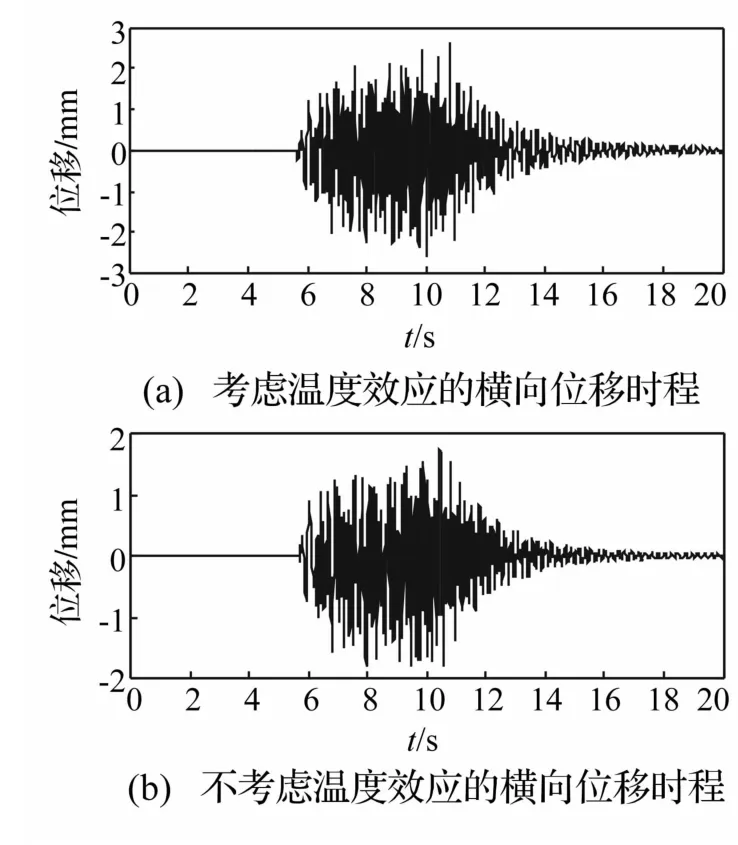
图9 跨中横向位移时程Fig．9 Lateral displacement history ofmidspan

图10 跨中横向加速度时程Fig．10 Lateral acceleration history ofmidspan

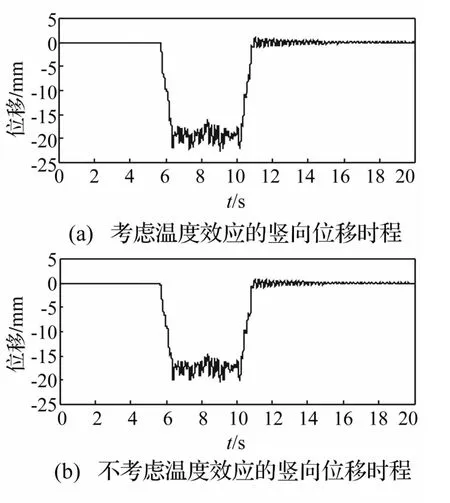
图11 跨中竖向位移时程Fig．11 Vertical displacement history ofmidspan

3．3．1 钢桥结构动力响应

以第六跨为例，图9～图10显示了考虑温度效应16∶30时刻（温度影响最不利时刻）和不考虑温度效应两种工况下的桥梁跨中横向位移和加速度响应时程，图11～图12给出了两种工况下桥梁跨中竖向位移和加速度响应时程。表4列表分别显示出8∶30时刻、16∶30时刻和不考虑温度效应时桥梁的动力响应值。

表4 典型时刻桥梁动力响应峰值Tab.4 Peak dynam ic response of bridge at typicalmoment

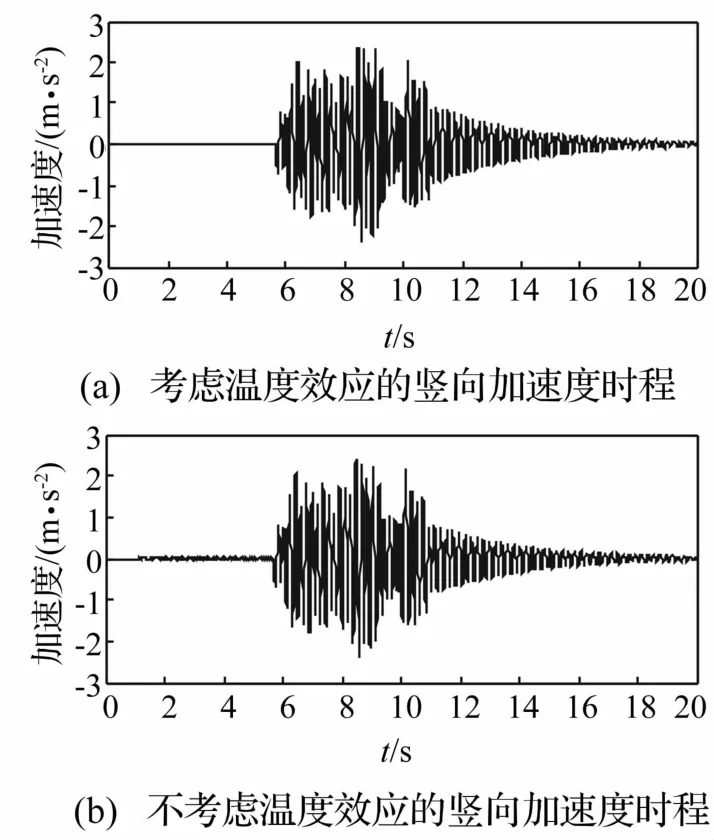
图12 跨中竖向加速度时程Fig．12 Vertical acceleration history ofmidspan

由以上计算结果可以发现，桥梁温度变形使得桥梁的竖向位移和横向位移均有所增加，其中横向最大位移增大显著。对比加速度峰值，横向加速度和竖向加速度均未出现明显差异。这是因为车桥系统采用温度效应引起的梁体变形和轨道不平顺叠加作为外部激励。梁体变形的波长特性属于长波范畴，而桥跨结构振动多由短波因素控制，因此温度效应对桥梁加速度没有明显影响。而从表4可知，在轨道横向和竖向相对位移的绝对值均较大的8∶30和16∶30时刻，由温度效应引起的桥梁动力响应的位移和加速度峰值非常接近，说明此两时刻下轨道变形虽方向不同，但变形幅值相近，因而对桥梁动力响应的影响基本相同；同时也表明温度效应确实对桥梁动力响应带来较为显著的影响。

3．3．2 列车动力响应

根据车辆运行安全性和平稳性指标，图13～图14显示了温度效应下16∶30时刻车体加速度和轮轨力时程。表5对两种时刻和无温度效应下下车辆运行安全性和平稳性指标及差值百分比等进行了对比。

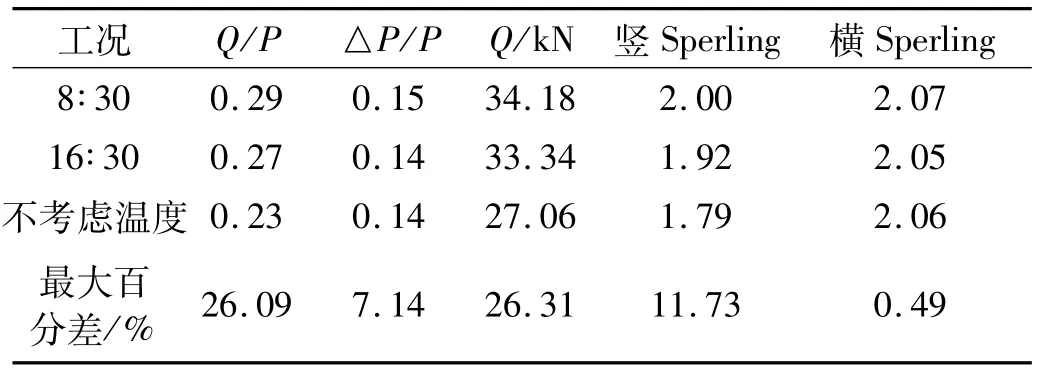
表5 行车指标最大值对比Tab.5 Contrast of themaximum indices of running train

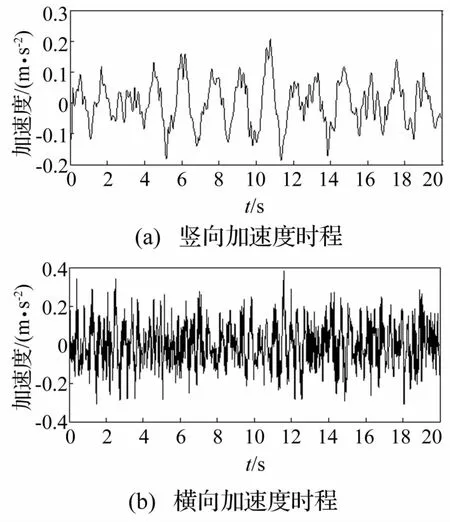
图13 车体加速度时程Fig．13 Vertical and lateral acceleration history of train

图14 轮对轮轨力时程Fig．14 Vertical and lateral wheel-rail forces history

由计算结果可以看出，考虑日照温度效应下的列车安全性及舒适性各项指标基本均变大。其中，脱轨系数较无温度荷载时最大增加26．09%，轮对横向力最大增加7．12 kN，竖向Sperling指标最大增加0．21。根据我国铁道部标准《铁道机车动力学性能实验鉴定方法及评定标准》（TB／T2360－93）和《铁道车辆动力学性能评定和试验鉴定规范》（GB5599－85），计算结果表明，行车各指标虽未超过规范限制，但在日照温度效应下有较大增长。

4 结 论

本文通过铁路简支钢板梁桥在日照作用下温度场和位移场的建立和分析，计算得到日照温度效应下，列车以160 km／h的速度通过该桥时，桥梁结构的位移、加速度响应以及列车走行安全及舒适性指标的最大值。计算发现，桥梁横向位移增大显著，列车脱轨系数、轮轴横向力、竖向Sperling指标等有大幅增加，虽未超过规范规定安全限制，但导致行车安全性和平稳性级别降低，故在车桥系统设计研究中，应考虑日照温度效应的影响。

［1］陈波，郑瑾，王建平．桥梁结构温度效应研究进展［J］．武汉理工大学学报，2010，32（24）：79－83．

CHEN Bo，ZHENG Jin，WANG Jian-ping．State-of-the-art of the temperature effects of bridge［J］．Journal of Wuhan University of Technology，2010，32（24）：79－83．

［2］Zuk W．Thermal behavior of composite bridges-insulated and uninsulated［J］．Highway Research Record，1965（76）：231－253．

［3］Kehlbeck F．Einfluss der Sonnenstrahlung bei Bruckenbauw erken［M］．Dusseldorf：Werner-Verlag，1975．

［4］American Association of State Highway and Transportation Officials（AASHTO）．LRFD Bridge design specifications［S］．Washington，D．C．，2012．

［5］Tong M，Tham LG，Au F T K，et al．Numericalmodeling for temperature distribution in steel bridges［J］．Computers and Structures，2001，79（6）：385－397．

［6］刘兴法．混凝土结构的温度应力分析［M］．北京：人民交通出版社，1991．

［7］孙国晨，关荣财，姜英民，等．钢－混凝土叠合梁横截面日照温度分布研究［J］．工程力学，2006，23（11）：122－127．

SUN Guo-chen，GUAN Rong-cai，JIANG Ying-min，et al．Sunshine-induced temperature distribution on cross section of steel-concrete composite beams［J］．Engineering Mechanics，2006，23（11）：122－127．

［8］任志刚，胡曙光，丁庆军．太阳辐射模型对钢管混凝土墩柱温度场的影响研究［J］．工程力学，2010，27（4）：246－250．

REN Zhi-gang，HU Shu-guang，DING Qing-jun．Research on the effect of solar radiation model on temperature field of concrete-filled steel tube pier［J］．Engineering Mechanics，2010，27（4）：246－250．

［9］谢肖礼，赵国藩，胡安妮等．钢管混凝土拱桥施工过程中考虑温度效应的预抬高量二阶分析［J］．工程力学，2005，22（4）：62－66．

XIE Xiao-li，ZHAO Guo-fan，HU An-ni，et al．The secondorder analysis of preraised height of concrete-filled steel tube arch bridge during construction considering temperature effect［J］．Engineering Mechanics，2005，22（4）：62－66．

［10］Wang ML．Load and environmental effects of a damaged PCbox girder bridge［C］．The 4th InternationalWorkshop on Advanced SmartMaterials and Smart Structures Technologies．Tokyo：［s．n．］，2008．

［11］Liu C Y，DeWolf J T．Effect of temperature on modal variability of a curved concrete bridge under ambient loads［J］．Journal Structural Engineering ASCE，2007，133（12）：1742－1751．

［12］Xia Y，Hao H，Zanardo G，et al．Long term vibration monitoring of a RC slab：temperature and humidity effect［J］．Engineering Structures，2006，28（3）：441－452．

［13］Chen B，Xia Y．Thermal effects of Tsing Ma suspension bridge［R］．Hong Kong：The Hong Kong Polytechnic University，2009．

［14］彭友松．混凝土桥梁结构日照温度效应理论及应用研究［D］．成都：西南交通大学桥梁与隧道工程，2007．

［15］杨世铭，陶文铨．传热学［M］．4版．北京：高等教育出版社，2006．

［16］翟婉明，夏禾．列车－轨道－桥梁动力相互作用理论与工程应用［M］．北京：科学出版社，2011．

［17］夏超逸．撞击荷载作用下车桥系统的动力响应及高速列车运行安全研究［D］．北京：北京交通大学桥梁工程，2012．

［18］夏禾，张楠．车辆与结构动力相互作用［M］．2版．北京：科学出版社，2005．

Tem perature effect on running performance of steel railway bridge

TIAN Yuan，ZHANGNan，SUN Qi，DU Xian-ting，XIAHe
（School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China）

The temperature effect induced by sunshine causes obvious deformation of railway bridges and affects the running safety of trains．In order to calculate the rail deformation，the temperature field and displacement field were analyzed making use of the heat-stress coupled technology of finite element software ANSYS，in which the boundary conditions of bridge in thermal analysis were determined based on some solar physics comprehensive factors of thermal radiation，heat convection and heat conduction and related empirical formulas．The component section segmentation was proposed in themodel simplification．A train-bridge interaction system modelwas established．Taking the bridge thermal deformation and track irregularity as external excitations，the inter-system iterationmethod was used to solve the interacted system．As a case study，a typical simply-supported steel plate girder bridge was concerned to analyse the vehicle-bridge interaction．The results show that temperature effect has little influence on bridge accelerations when a train is passing through．However，the safety and comfort status become worse due to the increase of bridge horizontal and vertical deformation．

train-bridge coupled vibration；temperature effect；thermal analysis；running safety；steel railway bridge

U448．13

A

10．13465／j．cnki．jvs．2015．12．017

国家重点基础研究发展计划973项目（2013CB036203）；高等学校博士学科点专项科研基金资助项目（20130009110036）；中央高校基本科研业务费专项资金（2014YJS096）

2014－02－19 修改稿收到日期：2014－06－24

田园男，博士生，1988年生

张楠 男，教授，博士生导师，1971年生