含不确定性参数的复合材料薄壁结构吸能特性评估方法研究

冯振宇，赵彦强，陈艳芬，解 江

（中国民航大学天津市民用航空器适航与维修重点实验室，天津 300300）

含不确定性参数的复合材料薄壁结构吸能特性评估方法研究

冯振宇，赵彦强，陈艳芬，解 江

（中国民航大学天津市民用航空器适航与维修重点实验室，天津 300300）

由于复合材料性能分散度大、加工精度较低，为复合材料薄壁吸能结构引入了不可忽略的不确定性因素，为此，提出了一种含不确定参数的复合材料薄壁结构吸能特性的评估方法并进行了算例研究。复合材料薄壁圆管是一种典型的吸能元件，圆管的壁厚和内径是对其吸能特性有显著影响的特征几何尺寸，考虑了这两个参数的不确定性，在准静态压溃的条件下评估了薄壁圆管的引发比应力和比吸能这两个关键吸能指标。首先，利用区间分布来描述壁厚和内径的不确定性，其次应用有限元方法建立区间内不确定参数和结构吸能特性指标间的二阶响应面函数，最后对响应面函数进行区间摄动从而确定吸能特性指标的分布区间。算例研究结果显示，与比吸能相比，引发比应力受壁厚和内径不确定性的影响更大。此外，相比于内径，壁厚的不确定性对吸能特性影响更显著，因此为获得稳定的结构吸能特性应尽量提高复合材料圆管壁厚的加工精度。

复合材料薄壁结构；吸能特性；不确定性；区间模型；有限元分析

复合材料因其高比强度、高比模量等优异性能，在飞机结构中的应用比例越来越大，由于其损伤、破坏和失效模式与金属结构显著不同，导致飞机结构的抗坠撞性能随着复合材料结构成为主承力结构或出现在主传力路径上而发生明显改变［1－2］。因此，复合材料结构在飞机坠撞过程中的吸能特性及其吸能设计近年来受到了国内外工程、学术界的广泛关注［3－4］。

无论金属还是复合材料，薄壁结构都是一种典型的吸能结构形式，如薄壁圆管、方管和波纹板等。薄壁结构具有刚度大、稳定性好和吸能效率高的特点。不同的是，复合材料的力学性能比金属材料的分散性大，复合材料薄壁结构的成型工艺也更复杂，实际工程中由于加工精度的限制和材料性能的分散性导致复合材料薄壁结构的几何尺寸和物理性能具有不可忽视的不确定性［5］。这些参数的微小变化都会改变结构的力学响应特性和失效破坏模式，从而影响其吸能特性，导致在工程中不得不通过大量实验来确定复合材料薄壁结构破坏吸能的力学行为。除了试验方法，针对应用于飞行器和汽车上的复合材料吸能薄壁结构，研究人员近年来也做了大量的仿真分析工作［6－8］。数值仿真主要采用显式求解结构有限元的数值方法模拟复合材料结构破坏吸能这一瞬态强非线性过程，常用LS-DYNA、MSC-DYTRAN和PAM-CRASH大型商用有限元软件。但这类研究通常以几何／材料参数的名义值或平均值建立确定性模型作为研究对象进行分析，忽略材料性能和结构尺寸等参数分散性，计算分析结果与实验值往往存在较大差异。可见，用常规的确定性的方法已经很难评估和分析这种不确定来源多、分散度大的复合材料结构和非线性力学问题。综上，在进行复合材料薄壁结构吸能特性分析时引入不确定性理论、建立含不确定参数的复合材料薄壁结构吸能特性的评估方法工程意义显著。

当前已有学者应用不确定性理论在线性范围内来研究复合材料结构的力学问题。张丽娟［9］利用区间方法对考虑材料参数不确定性的复合材料层合板屈曲问题进行了研究，苑凯华［10］利用区间方法对考虑几何参数和材料参数不确定性的复合材料壁板的颤振问题进行了研究。上述研究表明运用区间方法可以有效的建立含不确定参数的复合材料结构模型并预测其可能的力学行为。由于结构碰撞吸能是强非线性瞬态动力学问题，比隐式求解的线性力学问题复杂得多，将不确定理论用来研究结构吸能特性的案例还不多，仅有Salehghaffari对含不确定参数的金属圆管的吸能特性进行了研究。但对于复合材料薄壁结构其参数分散性更大，工程中受试验条件和成本的限制样本空间往往有限，有些参数如结构的特征尺寸等，无法得到精确的分布特征，难以通过文献［11］中所述方法确定结构的吸能特性。

在工程中通常难以得到复合材料薄壁结构中某些分散度大的重要参数的概率分布，而通常可以确定其取值范围的上下界。为此提出了基于区间的含不确定参数复合材料薄壁结构的建模方法和其吸能特性的分析方法。首先用区间对不确定参数进行描述，根据区间设计实验点，然后利用显式瞬态有限元对确定性参数的复合材料薄壁结构进行吸能特性分析，并采用响应面方法拟合出确定性薄壁结构吸能特性指标与结构参数间的响应面方程，最终通过对响应面方程进行区间分析确定含不确定参数的复合材料结构吸能特性指标的分布区间。并应用该方法对考虑加工公差的复合材料薄壁圆管在压溃载荷下的吸能特性进行分析，揭示几何特征尺寸的不确定性对复合材料薄壁圆管吸能特性的影响。

1 不确定参数的区间表示

复合材料薄壁结构的吸能特性与复合材料的弹性模量、剪切模量、密度以及结构的几何尺寸等参数有关，这些参数可用x1，x2…，xn表示，在确定性结构吸能特性分析中，常使用这些结构参数的确定值或中值xci，而在不确定性结构吸能特性分析中，还需要考虑结构参数不确定性的影响。通常对结构参数的不确定性信息掌握较少而难以确定其概率特性，而确定不确定参数的界限则相对容易，用区间符号可以表示为

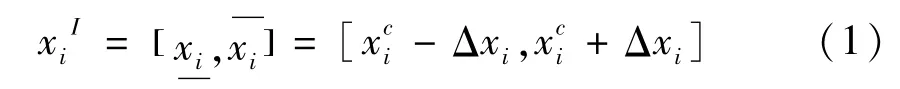
2 构建响应面

2.1 中心组合试验设计

为建立含不确定参数薄壁结构吸能特性评估模型，需要具备关于结构吸能特性指标与参数之间的函数关系。由于复合材料薄壁结构的破坏吸能机理复杂，无法建立解析的函数关系表达式，但可以根据数值计算结果，采用统计推断的方法拟合函数方程。本文采用响应面法，拟合参数区间内结构参数与吸能特性指标间的函数关系。

为以较小的计算或试验成本得到满足精度的响应面方程，需根据参数区间，通过实验设计来选择样本点。中心组合试验设计是响应面法研究中常用的实验设计方法，其试验点分布见图1。

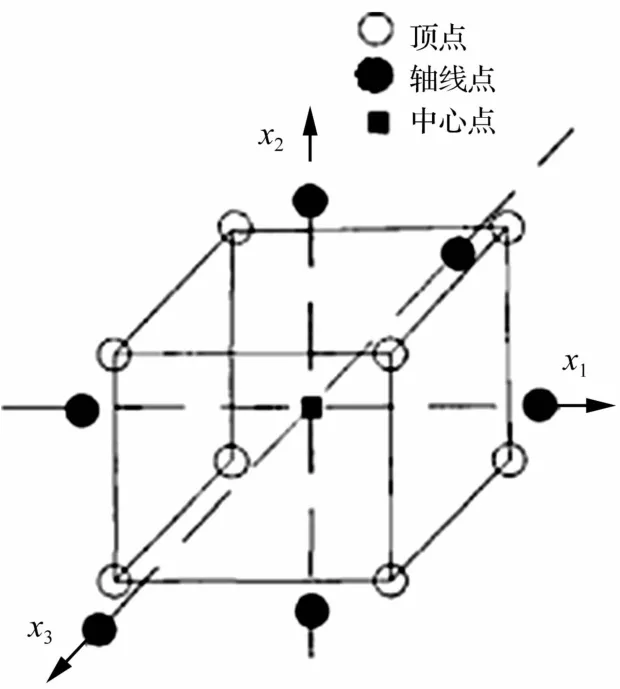
图1 中心组合设计实验点分布图Fig．1 Experimental point distribution of central composite design

对n（n≥2）个因素的中心组合设计需要进行的试验总数为N＝2n+2n+nc。试验由三个部分组成：2n个立方体顶点处的试验、2n个轴点处的试验及nc次中心点重复试验。通过中心点处的重复试验可以提高拟合方程的精度。中心点处重复试验次数与考察因素的关系见表1。

表1 中心组合设计的因素数与试验次数Tab.1 The number of factors and tests of central composite design

2.2 确定响应面方程

在确定响应面方程时折中精度要求和计算成本，采用二次多项式，并利用最小二乘原理确定多项式系数，得到响应和参数变量之间的函数关系。建立完全二阶响应面方程：式中为响应面近似函数；n为模型设计变量的数目；xi为模型设计变量；c0、ci、cii和cij为响应面方程待定系数。

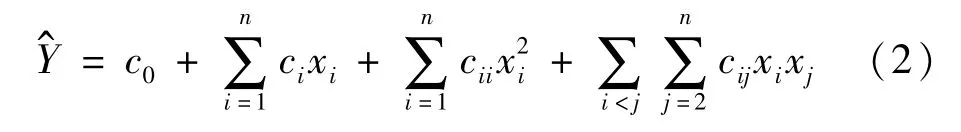
由试验设计确定的m个样本点组成设计变量矩阵X，通过确定性分析方法计算样本点的吸能特性向量Y；计算值与响应面拟合值的误差组成的向量为ε，各矩阵向量之间的关系

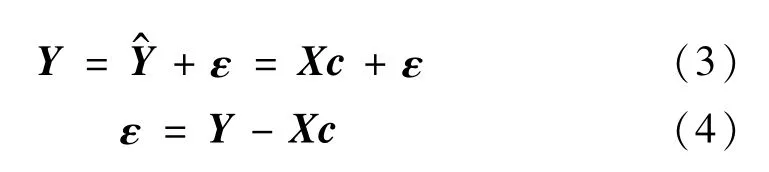
待定多项式系数向量c用最小二乘法拟合求解：

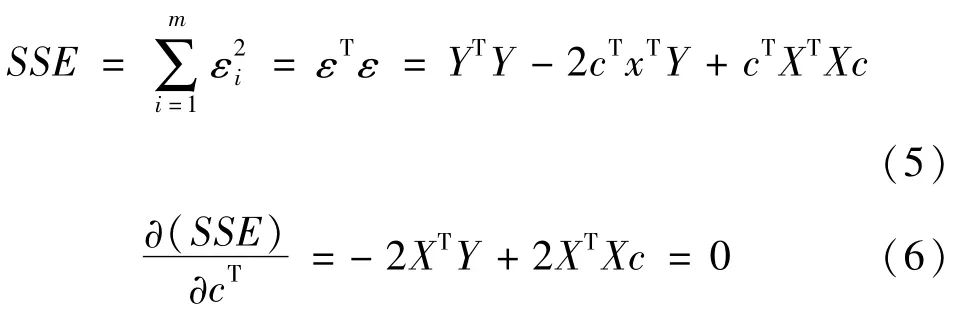
式中；SSE为误差平方和。系数向量c的估计为：

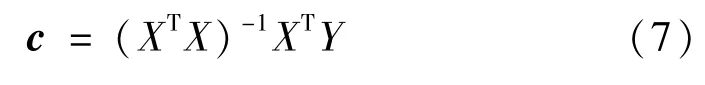
由此得到响应面方程后，为检验响应面拟合程度需进行R2检验

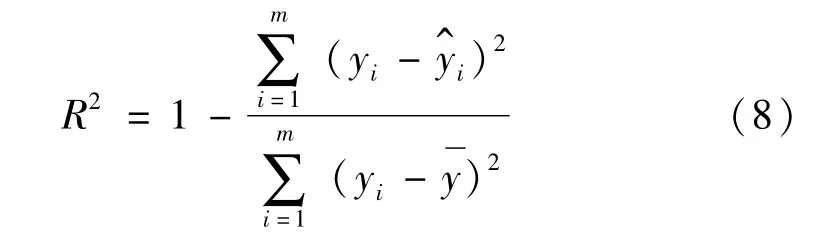
3 吸能特性指标区间的确定

确定在参数区间对应的响应面方程的解区间，就可得到含不确定参数的复合材料结构吸能特性指标的分布区间，采用区间摄动法来确定响应面方程的解区间。

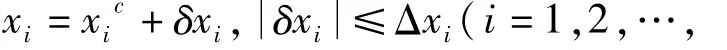
来衡量区间的分散度，K值越大区间越分散。

4 含不确定参数复合材料吸能特性评估流程

评估含不确定参数复合材料吸能特性，首先应对参数进行初步筛选，并确定待考虑参数的分布区间；根据参数的分布区间，利用中心组合设计实验设计方法安排实验点；使用LS-DYNA计算实验点的响应值；根据计算结果确定响应面方程；利用区间分析方法，确定吸能特性的分布区间。图2给出含不确定参数复合材料薄壁结构建模和其吸能特性评估的流程。

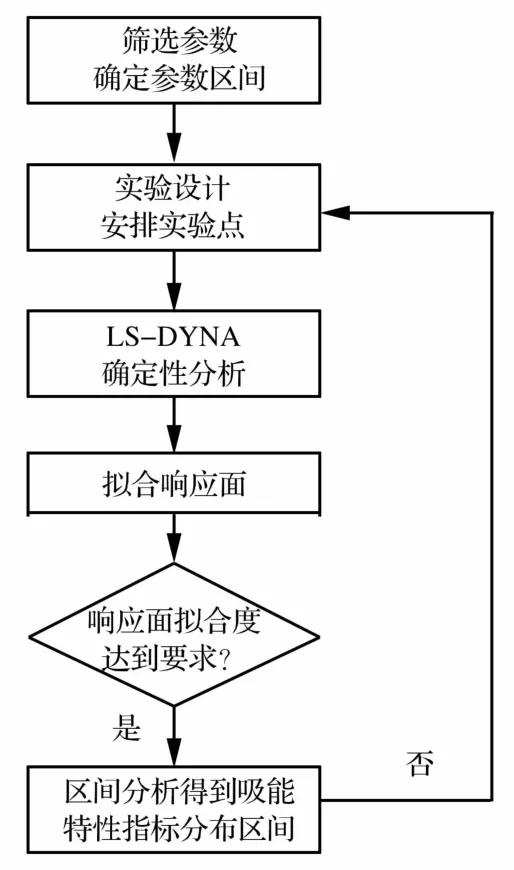
图2 含不确定参数复合材料吸能特性评估流程图Fig．2 The flow chart of analyzing energy absorbing characteristics of composite structure with uncertain parameters

5 算 例

5.1 吸能特性指标

采用比吸能、压溃比应力和引发比应力3个指标来描述结构在准静态轴向载荷作用下发生压溃破坏的过程中吸收能量的力学特性。

其中，比吸能（SEA）是结构有效压溃破坏长度内单位质量（m）所吸收的能量（EA）：

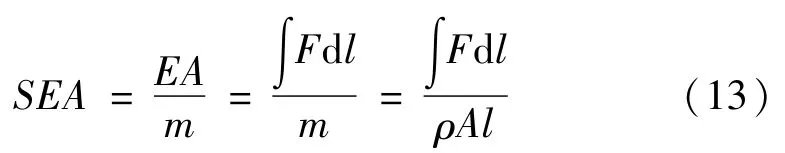
式中：ρ为材料密度，A为薄壁管横截面积，l为压溃长度。

压溃比应力（SCS）作为压溃载荷的评价指标是由压溃过程中的瞬时压溃力（F）除以薄壁管的密度（ρ）及横截面积（A）得到的：

引发比应力（TSS）是结构被压溃破坏的门槛值，用于评价结构在外力作用下发生破坏吸能难易程度的指

5.2 参数确定的复合材料圆管吸能特性分析

本文的基准模型为高100 mm，内径50 mm，壁厚1．84 mm，顶端外侧设有45°导角的复合材料薄壁圆管。圆管由14层碳纤维增强环氧树脂层合而成，其中牌号为T700的碳纤维体积分数为64．3%，薄壁圆管的铺层方式为［+45／－45／90／0／0／90／0］S，环氧树脂的牌号为QY8911。标，是比载荷－位移曲线的初始峰值。

在LS-dyna环境中使用Belytschko-Tsay壳单元建立了上述复合材料薄壁圆管的单层等效有限元模型。模型中单元特征长度为2mm，复合材料圆管选取MAT 54材料模型，具体材料参数见表2。圆管上方压板采用20号刚体材料，圆管底端节点固定约束，顶端为自由端。有限元模型共有4 378个壳单元，4 497个节点。文献［12］的研究表明使用Ls-dyna进行压溃仿真时，在加载速度小于40 km／h的条件下，薄壁圆管在不同加载速度下的“载荷－位移”曲线基本相同，并与准静态试验结果吻合。模拟仿真中，轴向压缩的加载速率设置为5 000 mm／s匀速加载，使用8个CPU核心并行计算，耗时369 s。图4给出了本次仿真与文献［6］中实验所得“载荷－位移”曲线的对比图。表3给出了仿真与实验所得吸能数据的对比。从图4和表3中可知仿真所得曲线和实验曲线较为吻合，引发比应力峰值误差3．59%，比吸能误差4．06%，仿真模型可用于接下来的研究工作。

图3 复合材料薄壁圆管有限元模型Fig．3 The finite elementmodel of the thin-walled composite tube

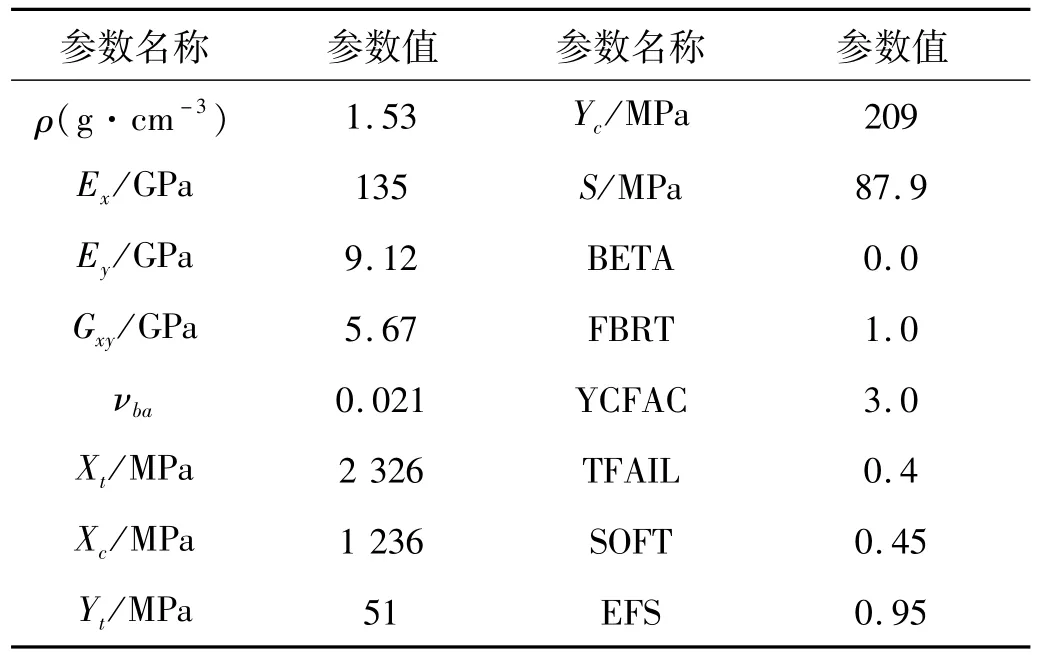
表2 复合材料薄壁圆管材料参数Tab.2 Material properties of thethin-walled composite tube

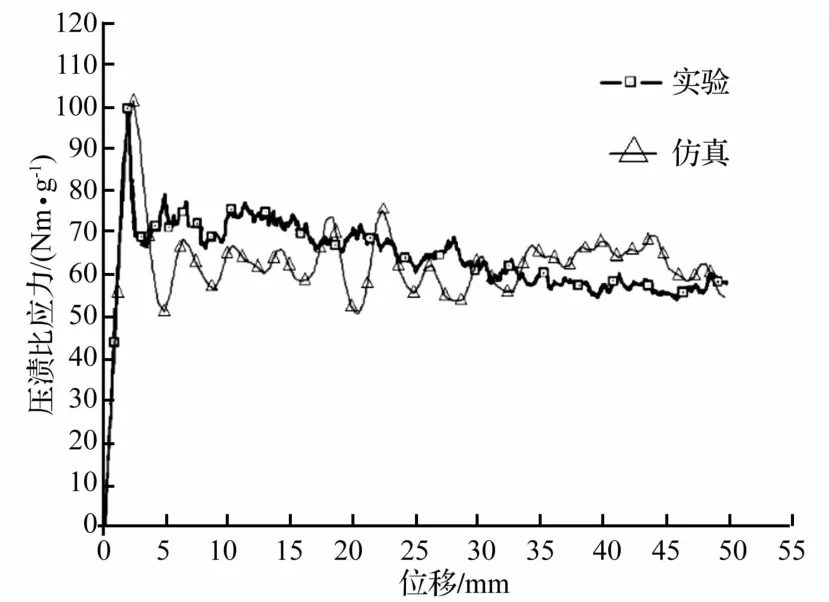
图4 本文仿真与文献［6］中实验所得压溃比应力－位移曲线Fig．4 Specific crushing stress-displacement curve

表3 实验与仿真所得吸能数据Tab.3 Energy absorption data of test and simulation

5.3 考虑尺寸不确定性圆管吸能特性分析

受加工工艺影响复合材料薄壁结构的特征尺寸存在较大分散性，这会对结构的吸能特性造成影响，将对考虑尺寸不确定性的复合材料薄壁圆管进行吸能特性分析。

根据HB5800－99未注尺寸公差极限偏差中对公差要求可知圆管加工尺寸为高100±0．43，内径为500－0．3，壁厚为1．840．12－0．12。

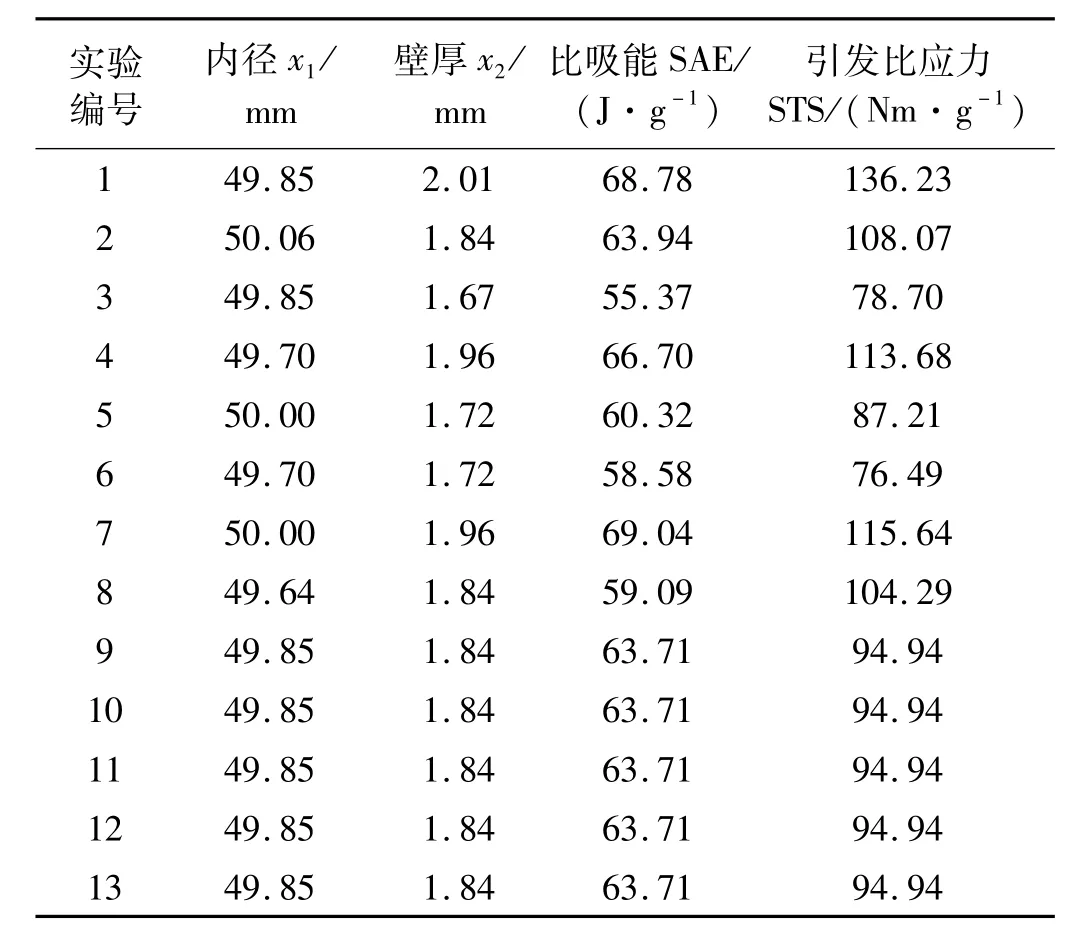
表4 实验点安排及计算响应值Tab.4 Test points arrangement and respond value calculation

比吸能和引发比应力的计算并不涉及结构整体高度，且在当前高度的变化范围内结构失效模式不会发生变化，为此高度方向的公差对吸能数据没有影响，因而在进行吸能特性计算时不考虑高度的不确定性。考虑内径和壁厚的分布区间x1I＝［49．7，50］，x2I＝［1．72，1．96］进行中心组合试验设计方法安排实验点，并利用前述仿真模型计算实验点的响应值见表4。

利用表4中数据，根据式（2）～式（7）确定响应面形式和待定系数值，得到响应面方程和响应面图。

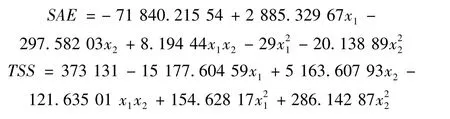
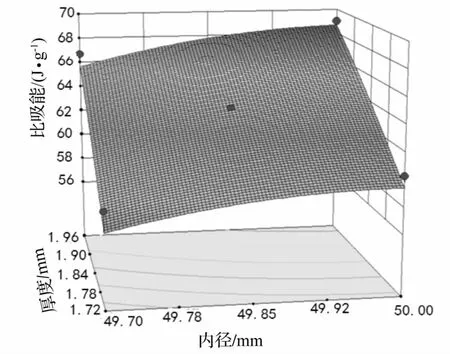
图5 比吸能响应面图Fig．5 The response surface figure of SAE

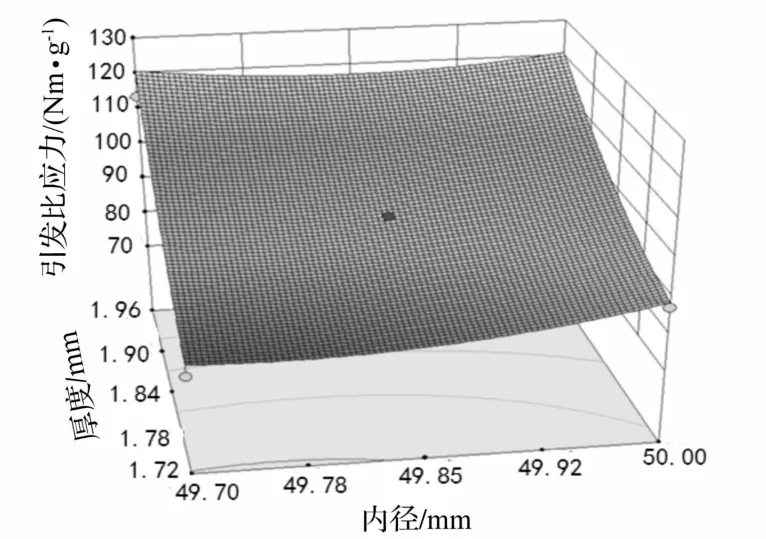
图6 引发比应力响应面图Fig．6 The response surface figure of TSS

根据式（8）对所得两个响应面方程进行R2检验R21＝0．957 9、R22＝0．941 0表明该响应面方程拟合度较好。

根据响应面方程和参数分布区间按照式（9）～式（11）确定该复合材料圆管比吸能和引发比应力的分布区间为SAE∈［56．84，70．58］，TSS∈［64．524，125．36］。根据式（12）计算SAE和TSS的区间分散度分别为0．11和0．32。由此可知：结构尺寸公差对引发比应力的影响更加显著。

文献［6］中加工了2个名义尺寸为D＝50，h＝1．84的复合材料圆管，其实际尺寸分别为D＝50，h＝1．84和D＝50，h＝1．82，材料体系与铺层方式均与本算例相同。并进行了压溃实验，所得比吸能分别为64．05 J／g和61．40 J／g，引发比应力分别为101．44 Nm／g和106．85 Nm／g。两次实验结果，均在估计的区间内，验证了所提方法的有效性。

仅考虑内径存在公差时xI1＝［49．7，50］，x2＝1．84，根据响应面方程和参数分布区间按照公式（9）～（11）进行计算得到比吸能区间为R11＝［61．69，65．73］，分散度K11＝0．03，引发比应力区间为R21＝［89．21，100．67］，分散度K21＝0．06。仅考虑壁厚存在公差时x1＝50，xI2＝［1．72，1．96］根据响应面方程和参数分布区间按照式（9）～式（11）进行计算得到比吸能区间为R12＝［59．00，68．42］，分散度K12＝0．07，引发比应力区间为R22＝［72．45，117．43］，分散度K22＝0．23。由此可知壁厚变化对结构吸能特性的影响要大于内径，因而为减小结构吸能特性指标的波动，应在条件允许的范围内尽可能提高壁厚的加工精度。

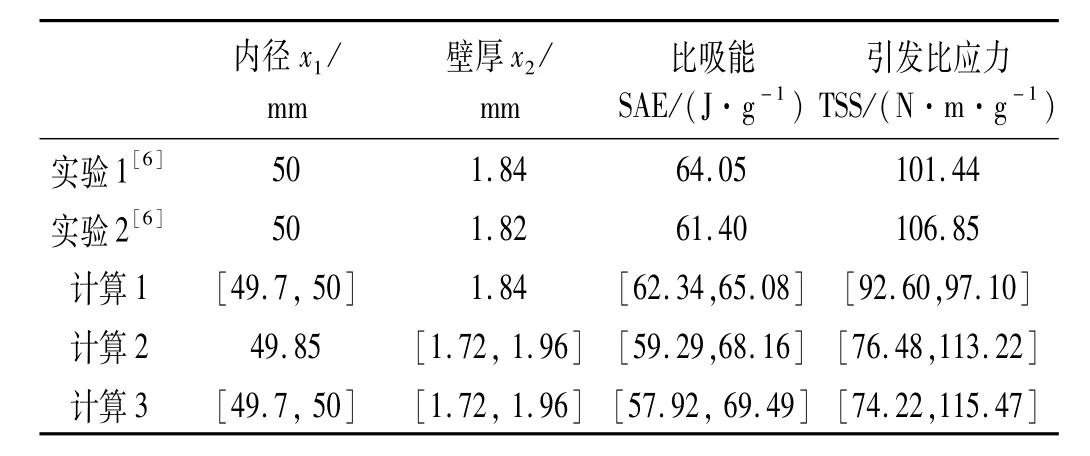
表5 实验与本分析方法所得结果Tab.5 Results of test and analysismethod

6 结 论

针对复合材料吸能薄壁结构存在较大不确定性，难以通过简单的实验或仿真确定其吸能特性的问题，提出了一种基于区间的复合材料薄壁结构吸能特性评估方法。本方法只需要不确定参数的上下界，不需要参数的分布特征，通过有限个实验点拟合响应面方程，不需要参数与响应间的函数关系，实用性较强。

采用响应面方法和中心组合实验设计方法，通过较小的计算量的解决了复合材料薄壁结构吸能特性指标与结构参数间没有通用的函数关系的问题，得到了拟合度较好的响应面方程。

在复合材料薄壁圆管结构的特征尺寸中，壁厚的不确定性对吸能特性的影响比内径的影响更为明显。壁厚的不确定性会对复合材料薄壁圆管引发比应力的影响要比对比吸能的影响更加显著。因此，在设计触发吸能圆管压溃的初始峰值时，要注意对圆管壁厚公差的控制。

［1］张弘，魏榕祥．通用飞机抗坠撞设计指南［M］．北京：航空工业出版社，2009．

［2］Fasanella E L．Multi-terrain impact testing and simulation of a composite energy absorbing fuselage section［R］．American Helicopter Society 60th Annual Forum．Baltimore：MD，2004．

［3］Mamalis A G．Crashworthy characteristics of axially statically compressed thin-walled square CFRP composite tubes：experimental［J］．Composite Structures，2004，63：347－360．

［4］Xiao Xin-ran．Modeling energy absorption with a damage mechanics based composite material model［J］．Journal of Composite Materials，2009，43：427－244．

［5］卢子兴，王晓英，俸翔．复合材料层合板临界屈曲载荷分散性［J］．复合材料学报，2013，30（1）：194－200．

LU Zi-xing，WANG Xiao-ying，FENG Xiang．Critiacl bucking load discrepancy of composite laminates［J］．Acta Materiae Compositae Sinica，2013，30（1）：194－200．

［6］Huang J C，Wang X W．Numerical and experimental investigations on the axial crushing response of composite tubes［J］．Composite Structures，2009，91：222－228．

［7］龚俊杰，王鑫伟．复合材料波纹梁吸能能力的数值模拟［J］．航空学报，2005，26（3）：298－302．

GONG Jun-jie，WANG Xin-wei．Numerical simulation of energy absorption capability of composite waved beams［J］．Acta Aeronautica et Astronautica Sinica，2005，26（3）：298－302．

［8］Joosten MW，Dutton S，Kelly D，et al．Experimental and numerical investigation of the crushing responseof an open section composite energy absorbing element［J］．Composite Structures，2011，93：682－689．

［9］张丽娟，邱志平．含不确定参数的复合材料层合板屈曲的两种非概率方法［J］．工程与建设，2008，22（3）：293－295．

ZHANG li-juan，QIU Zhi-ping．Two Non-probabilitymethods buckling analysis of composite laminated with uncertain parameters［J］．Engineering and Construction，2008，22（3）：293－295．

［10］苑凯华，邱志平．含不确定参数的复合材料壁板热颤振分析［J］．航空学报，2010，31（3）：119－124．

YUAN Kai-hua，QIU Zhi-ping．Thermal flutter analysis of composite panel with uncertain parameters［J］．Acta Aeronautica et Astronautica Sinica，2010，31（3）：119－124．

［11］Salehghaffari S，Rais-Rohani M．Evidence-based design optimization of energy absorbing components under material field uncertainty［A］．53rd AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics and Materials Conference［C］／／2012，Honolulu，Hawaii．

［12］王青春，范子杰．利用Ls-Dyna计算结构准静态压溃的改进方法［J］．力学与实践，2003，25（3）：20－23．

WANG Qing-chun，FAN Zhi-jie．Improvement in anslysis of quasi-static collapase with Ls-Dyna［J］．Mechanics in Engineering，2003，25（3）：20－23．

Evaluation method for energy-absorbing composite structureswith uncertain parameters

FENG Zhen-yu，ZHAO Yan-qiang，CHEN Yan-fen，XIE Jiang
（Tianjin Key Laboratory of Civil Aircraft Airworthiness and Maintenance，Civil Aviation University of China，Tianjin 300300，China）

Due to the large dispersion ofmaterial properties and inherentmachining tolerance，uncertain factors should be considered in designing and analyzing composite structures．An evaluation method for energy-absorbing characteristics of thin-walled composite structures with uncertain parameters was proposed and developed herein．Thinwalled composite tubes extensively applied in automobile and aircraft engineering are typical crushable elements for absorbing collision energy．The uncertainties due to machining tolerance of thickness and inner diameter of a tube were considered in the present paper and represented by an interval model．Triggering Specific Stress（TSS）and Specific Energy Absorption（SEA）were concerned and calculated by finite element method for indicating energy-absorbing characteristics of the specimen under quasi-static axial crushing．Response surface method was then used to build a second-order function between uncertain parameters and the two indicators of energy-absorbing characteristics．Interval perturbation of the response surface function was at last performed to establish the intervals of TSS and SEA respectively．The results show that，compared to SEA，TSS ismore affected by the uncertainty ofwall thickness and inner diameter．In addition，the effectof uncertainty ofwall thickness on energy-absorbing characteristics ismore significant than thatof inner diameter．The investigation reveals that themachining tolerance of composite tube should be limited as low as possible to keep designed energy-absorbing characteristics．

thin-walled composite structures；energy-absorbing characteristics；uncertainty；intervalmodel；finite element analysis

TB332

A

10．13465／j．cnki．jvs．2015．12．002

中央高校项目（ZXH2012B004）；中国民航局科技项目（MHRD20140207）

2014－04－21 修改稿收到日期：2014－06－13

冯振宇 男，博士，教授，1966年生