连接界面不定性对于加筋板结构振动能量传递特性的影响分析

纪 琳，黄震宇

（1.山东大学机械工程学院，济南 250061；2.上海交通大学电子信息与电气工程学院，上海 200240）

连接界面不定性对于加筋板结构振动能量传递特性的影响分析

纪 琳1，黄震宇2

（1.山东大学机械工程学院，济南 250061；2.上海交通大学电子信息与电气工程学院，上海 200240）

加筋板结构有着极为广泛的工程应用，准确预测振动能量（结构声）在加筋板中的传递特性是对于工程结构进行有效、合理声学设计的一个极为重要的环节。本文以板－筋－板组合系统为研究对象，将加强筋视为板件结构的中间连接件，通过仿真分析计算，研究了加筋板的参数不确定性对筋板组合系统的功率流传递特性影响。考虑到加强筋与所连接板件通常具有较大的动态特性差异，仿真模拟以中频混合分析法（Hybrid FE-SEAmethod）为主。研究表明：在长短波并存的中频域，加筋板中的结构声传递特性受加强筋刚度和边界条件变化的影响较大，而受其材料属性和连接自由度数量变化的影响较小。

振动传递；中频混合模型法；统计能量法；参数不确定性；加筋板结构

加筋板结构是构成飞机、航天器、汽车、火车、船舶等大型交通运载工具的重要结构类型，准确预测加筋板结构的振动噪声能量传递特性对于这些运载工具的舱室声学设计有着非常重要的工程意义［1］。

加筋板结构的动态特性表现在结构本身的振动响应及振动能量在加筋板各子结构间的传递［2－3］。加筋板结构的理论建模方法，一般可以按照结构尺寸与结构波波长的相对长短关系分为低频、中频和高频三个频域的分析方法［4］（注：与可测频率的高低可能不一致）。其中，低频域是指结构波波长远大于结构尺寸的情况，高频域指结构波波长远小于结构尺寸的情况，而中频域是指结构中既包含有长波子结构，又包含有短波子结构的情况。对于低频域，分析方法以传统的有限元、边界元法为主，对于高频域，以统计能量法分析为主，而对于中频域则以混合模型法为主［5］，即：将长波子系统用有限元模型构建，而对于短波子系统用统计能量法模拟［6］。在过去几十年中，针对加筋板结构振声响应的研究取得了长足的发展，尤其是对于加强筋与板之间存在较大动态特性反差的中频域，取得了一系列里程碑式的研究成果［7］。

然而，在现有中频研究方法和理论模型中，对于加强筋的动态模拟多以确定性分析方法为主［5－7］，即：假定加强筋的材料和尺寸、连接边界条件均为确定已知。显然，这一假定条件与实际工程中加强筋自身必然具有一定程度的参数不确定性这一事实不相符合。

为了揭示连接边界的参数不确定性对于加筋板整体结构振动能量传递特性的影响规律，本文选取具有典型中频振动特征的加筋板结构，针对加强筋的结构属性、材料属性、连接边界自由度数量及边界条件的不确定性对于振动能量的传递特性的影响进行了仿真分析研究，分别将加强筋的结构尺寸（如长度、高度等）和材料属性（如密度、阻尼损耗因子）视为围绕其名义参数值上下波动的随机参数，同时也探讨了当筋板之间的连接自由度数目存在某些不确定性以及加强筋自身的边界条件存在一定的不确定性条件下的影响特性。

由于实际工程中，加强筋一般可视为薄板件间的中间连接件；同时，考虑到加筋板结构通常存在着加强筋的波长远大于板件中的波长的关系，加筋板结构中的振动响应将在相当大的频域内呈现显著的中频振动特征，因此，本项研究中，对于加筋板振动能量传递分析主要是针对中频域，所用建模方法为当前中频振动领域影响力最为广泛的Hybrid FE-SEA方法［6－8］。

1 Hybrid FE-SEA混合模型理论

关于Hybrid FE-SEA的建模原理和方法的详细介绍请参见文献［7］。本文中，为了便于读者理解，作者先就一个简单的梁－板组合结构（如图1所示，其中f表示系统所受到的外部激振力向量，点力和／或分布力均可），对于Hybrid FE-SEA理论的振动能量传递计算过程简述如下。

图1 简单加筋板模型Fig.1 A simple rib-stiffened platemodel

首先，假定板具有足够的随机不定性［6］，那么，对于板可建立基于统计能量法（SEA）理论的能量平衡方程：

式中，左侧Ep表示板的统计能量响应，ηp和ηb，p则分别表示板的阻尼损耗因子和梁板间的能量传递系数（power transmission coefficient）；而式（1）右侧的则表示在外部激振力矢量f的作用下，由梁输入到板的功率流，分别可表达为［6］：

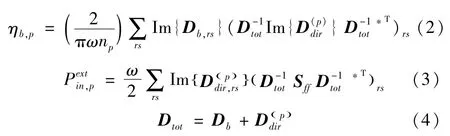
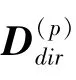
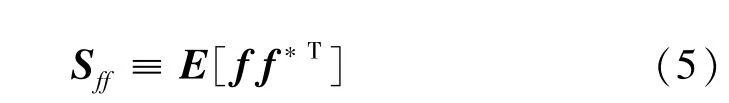
式（5）中，E[·]表示群体平均。

将式（4）～（5）代入到式（2）～（3），进而代入到式（1），就能够得出板的统计能量响应Ep，再根据统计能量法理论可得出由外部激振力传递到板中的平均功率流为：

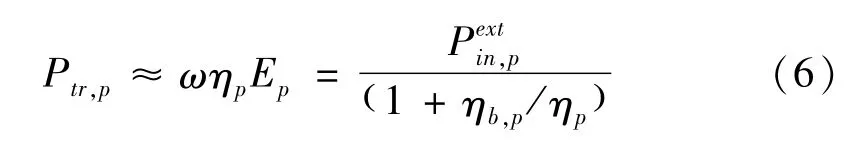
当加筋板结构中包含多个板子结构时（如图2所示的板－梁－板组合结构），可以将式（1）～（4）拓展为矩阵形式并进行相应的求解，从而得出由外部激振力f分别传递到各个板子结构中的平均功率流及统计能量响应情况［7－8］。

2 加筋板模型描述

图2所示的加筋板结构为由板1和板2通过梁（加强筋）联接而构成，其中，假定梁的边界条件为两端自由，而两个板的边界条件为：与加强筋平行的边界为简支，而另外两对边为自由边界条件，各子结构的材料和尺寸参数分别示于表1和表2。

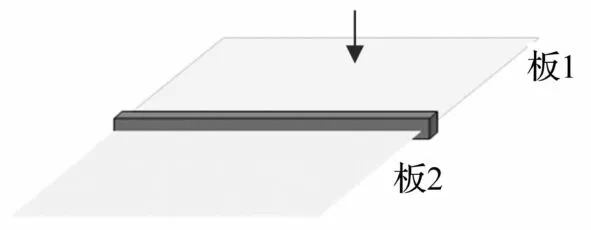
图2 板－筋－板组合模型Fig.2 A plate-beam-plate couplingmodel

当板1在任意位置处受到一个点简谐激振力的作用时，振动能量输入到板1中，进而通过中间连接件（梁）传递到板2中。

图3所示为板1和板2通过中间加强筋相联和无加强筋直接相联的平均功率流传递的对比情况。这里所采用的平均功率流的计算方法如下：首先，激励点位于板1上的位置用随机选取的方式选用了7个不同的位置；其次，对于每一个激励位置，采用子系统模态法［7］得出时间平均传递功率流的精确计算值；最后，对于所有激励位置处所对应的时间平均传递功率流计算结果进行空间平均，得出结构在统计能量法（SEA）意义上的平均传递功率流。

这里应该指出：在子系统模态法的计算过程中，梁和板之间的线连接形式采用间隔为1／4波长（板的弯曲波）的均布离散点连接形式来模拟，显然，由于板的弯曲波长随着频率的升高而减小，对于相同尺寸的线连接来说，所需连接点的数量将随着频率的提高而增大，计算耗时也逐渐增加。

表1 材料特性参数（钢）Tab.1 Parameters ofmaterial properties

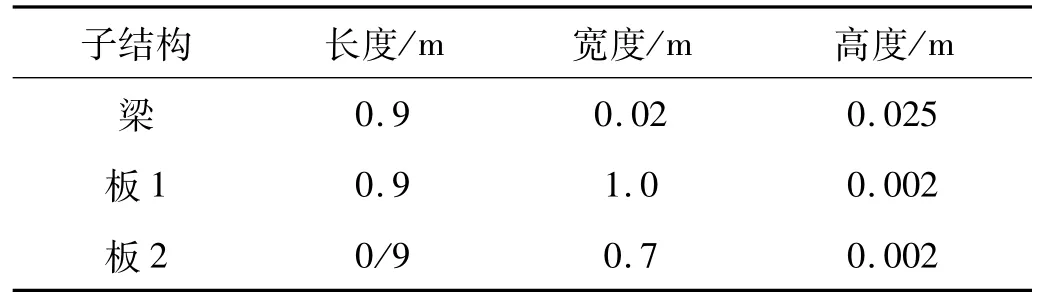
表2 尺寸特性参数（板1－梁－板2）Tab.2 Parameters of geometry properties

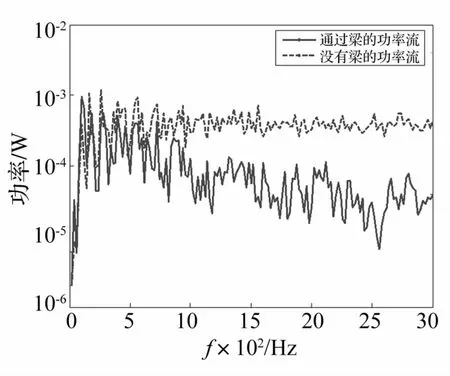
图3 板1与板2间的平均传递功率流Fig.3 Power transmission between plate 1 and plate 2

由图3可见：中间加强筋的存在能够显著降低板结构间的能量传递，显然，梁的动态特性对于系统的功率流传递特性能够产生很大的影响，这就使得研究加强筋的参数不确定性对于加筋板结构功率流传递的影响具有十分重要的意义。

3 计算结果及分析

对于图2所示的加筋板结构，由其参数特性（表1、表2）可知：筋的模态密度远低于板的模态密度，这就意味着加筋板结构的振动特性将以中频振动为主，因此，本节对于结构中功率流传递特性的计算中采用了本文第一节所述的Hybrid FE-SEA理论。

图4中对比了梁的长度和高度与其名义尺寸相比分别变化5%时对于结构中传递功率流的影响情况。可见：随着频率的增大，即使是梁的结构尺寸的微小变化亦能够对于传递功率流的峰值位置产生较大的影响，这就意味着：连接界面刚度的微小变化对于加筋板振动能量的传递的影响程度随着频率的升高而增大；同时，图4亦表明：增大梁的刚度，能够在一定程度上减少加筋板结构振动能量的传递。

图5对比了梁的边界条件分别为两端自由和两端简支条件下，结构中振动能量传递的计算结果。由图5可见：加强筋自身的边界条件的改变能够对于结构的振动能量传递的峰值和谷值的位置产生显著影响，这就使得对于一个特定的频域而言，减小加筋板结构的结构声传递性能有可能通过改变加强筋的边界条件来实现，如：图5中，对于频率范围（1 200，1 600）Hz和（1 900，2 400）Hz而言，梁的边界条件为两端简支时的传递功率流显著低于两端自由时的传递功率流。

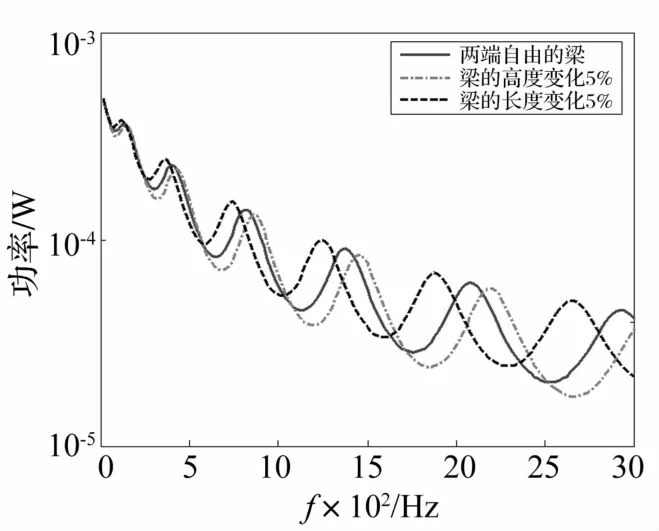
图4 梁的结构尺寸参数对于结构传递功率流的影响对比Fig.4 Comparison of transmitted power when the dimensional parameters of the beam are varied

图5 梁的边界条件对于结构传递功率流的影响对比Fig.5 Comparison of transmitted power when the boundary conditions of the beam are varied

然而值得注意的是，图5亦同时表明：对于宽频激励，加强筋边界条件的变化对于结构的功率流传递的平均水平的影响随着频率的增大而减小，也就意味着：连接边界处两端的具体边界条件对于板1与板2之间的有效耦合因子的影响随着频率的增加而减小。

图6对比了当作为连接件的梁的质量密度在－5%～+5%变化时，对于板1与板2间的传递功率流的影响。由图可见：连接边界处质量密度的变化对于加筋板振动能量传递的影响程度弱于连接边界刚度变化的影响。

图7对比了加强筋的阻尼特性的变化对于传递功率流的影响，表明：即使是在梁的材料阻尼值呈现20%的大幅度变化时，其对于加筋板结构的振动能量传递的影响也几乎可以忽略不计。这就意味着：增大连接界面处的阻尼值，并不能够有效降低板之间的结构声传递水平。

图8对比了连接界面自由度数量（即模拟梁板间连续线连接所采用的连接点数量）对于加筋板结构声传递预测结果的影响情况，这里，梁与板之间的实际连续线连接用一组均匀分布的离散连接点模拟，而连接点数量的变化通过改变相邻连接点之间的间距来实现。图8中连接点的间距分别采用了板的弯曲波长的一半、三分之一和四分之一的情况，由图可见：连接边界自由度数量的变化对于加筋板中的结构声传递特性影响主要体现于谷值域，而对于峰值处的影响相对较小。

图6 梁的质量密度对于结构传递功率流的影响对比Fig.6 Comparison of transmitted power when the mass density of the beam material is varied

图7 梁的阻尼损耗因子对于结构传递功率流的影响对比Fig.7 Comparison of transmitted power when the damping loss factor of the beam is varied

图8 连接界面自由度数量对于结构传递功率流的影响对比Fig.8 Comparison of transmitted power when the numbers of interface degrees of freedom（DOFs）are varied

4 结 论

加筋板作为若干工程结构中的重要组成部分，其结构声传递特性对于实现工程结构的减振降噪设计有着非常重要的影响作用。由于加强筋通常可视为不同板件间的连接边界，且加强筋与所连接板件通常存在着显著的动态特性差异（如加强筋的振动主要表现为长波变形，而板件振动以短波局部变形为主），因此，本文用加筋板的参数变化来模拟连接边界处的参数不确定，并采用中频混合模型法（Hybrid FE-SEA Method）作为主要分析方法，通过一个板－筋－板的简单加筋板模型，对于连接边界的参数不确定性的结构声传递影响规律进行了仿真计算分析。

研究结果表明：在长、短波并存的中高频域，连接边界对于加筋板的振动能量传递特性（即：结构声传递）能够产生较大的影响，尤为表现为连接界面处刚度和边界条件的不确定性，而连接界面处的材料特性（如质量密度和阻尼特性）等参数不确定性对于加筋板中结构声传递的影响较小。

以上研究结论将对采用商用软件（如VA-One［6］等）建立诸如飞机、高铁、潜艇等的舱室筋板结构的中频声振响应预测分析模型时，如何引入连接边界的参数不确定性的影响提供有效借鉴。

［1］Galbrun L.Vibration transmission through plate／beam structures typical of lightweight buildings：Applicability and limitations of fundamental theories［J］.Applied Acoustics，2010，71：587－596.

［2］乔百杰，赵彤，陈雪峰.功率流测量以及振动能量参数估计试验研究［J］.振动与冲击，2014，33（7）：194－198.

QIAO Bai-jie，ZHAO Tong，CHEN Xue-feng.Tests for power flow measurement and vibrational energy estimation［J］.Journal of Vibration and Shock，2014，33（7）：194－198.

［3］薛开，王久法，李秋红，等.中厚矩形板的振动功率流特性分析［J］.振动与冲击，2013，32（21）：178－181.

XUE Kai，WANG Jiu-fa，LIQiu-hong，etal.Vibration power flow analysis of moderately thick rectangular plates［J］.Journal of Vibration and Shock，2013，32（21）：178－181.

［4］Soize C.A model and numerical method in the medium frequency range for vibroacoustic predictions using the theory of structural fuzzy［J］.Journal of the Acoustical Society of America，1993，94：849－865.

［5］DesmetW.Mid-frequency vibro-acoustic modelling：challenges and potential solutions［C］／／Proceedings of International Conference on Noise and Vibration Engineering.Leuven：Leuven University，2002：835－862.

［6］Shorter P J，Langley R S.Vibro-acoustic analysis of complex systems［J］.Journal of Sound and Vibration，2005，288：669 －700.

［7］纪琳.中频分析方法［M］.北京：机械工业出版社，2013.

［8］PAM VA-One用户手册.ESI集团，2013.

Effects of ribs'parameter uncertainty on vibration energy transm ission of Rib-stiffened p late structures

JILin1，HUANG Zhen-yu2

（1.School of Mechanical Engineering，Shandong University，Jinan 250061，China；2.School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University，Shanghai200240，China）

It is of great importance to predict the vibration energy transmission（structure-borne sound transmission）within rib-stiffened plate structures due to their large applications in practical engineering.Since ribs usually were taken as junctions between plates，here parameter uncertainty effects of stiffening beams（ribs）on the power transmission between coupled thin plates were studied based on a plate-beam-plate model.Considering the significant dynamic features'mismatches between the ribs and plates，the hybrid FE-SEA method was adopted for simulations.Numerical investigations showed that the variations of stiffness and boundaries of ribs have relatively bigger effects on the vibration energy transmission of ribs-stiffened plate structures than the variations of material properties and interface coupling DOFs do.

vibration transmission；mid-frequency hybrid FE-SEA theory；statistical energy analysis（SEA）；parameter uncertainty；rib-stiffened plate structures

TB53；TH212

A

10.13465／j.cnki.jvs.2015.21.032

国家国际科技合作专项资助项目（2012DFG01790）；国家自然科学基金（51175300）

2014－05－08 修改稿收到日期：2014－06－17

纪琳女，博士，教授，1967年9月生

黄震宇男，博士，副教授，1975年1月生