齿轮箱振动信号的分数阶时频谱多重分形特征提取研究

张云强，张培林，吴定海，李 兵

（军械工程学院车辆与电气工程系，石家庄 050003）

齿轮箱振动信号的分数阶时频谱多重分形特征提取研究

张云强，张培林，吴定海，李 兵

（军械工程学院车辆与电气工程系，石家庄 050003）

针对齿轮箱振动信号的非线性和非平稳性，提出一种基于Q阶加权矩结构分割函数法的分数阶时频谱多重分形特征提取方法。首先构造时频分辨率较好的分数阶S变换技术获取齿轮箱振动信号的分数阶时频谱；然后针对分数阶时频谱的特点，设计出一种Q阶加权矩结构分割函数法，用于提取分数阶时频谱的多重分形特征参数。对5种状态的齿轮箱振动信号进行了分析和研究，结果表明齿轮箱振动信号的分数阶时频谱具有多重分形特性，Q阶加权矩结构分割函数法提取的多重分形特征参数能有效描述分数阶时频谱的多重分形特征。

齿轮箱；时频分析；多重分形；Q阶矩结构分割函数法；分数阶S变换

齿轮箱是机械设备中常用的传动部件，其振动信号是一种典型的非线性、非平稳信号［1－2］。如何提取有效的特征参数描述不同状态的齿轮箱振动信号，从而准确诊断和识别齿轮箱故障，一直是众多研究人员致力追求的目标。

时频分析技术能将信号映射到二维时－频面内，从而有效描述信号的时频局部特性，是处理非平稳信号的主要手段。目前，常用的时频分析技术有短时Fourier变换、Wigner-Ville分布、小波变换和S变换等［3－6］。其中S变换是一种较新的时频分析技术，虽然克服了短时Fourier变换和小波变换的不足，但是对高频信号的频率分辨率较差。分数阶Fourier变换［7］作为Fourier变换的一种推广，具有良好的时频旋转特性。为改善S变换对高频信号的频率分辨率，从而提高S变换整体的时频分辨性能，利用分数阶Fourier变换的时频旋转特性，设计了一种分数阶S变换，并用于齿轮箱振动信号分析。

分数阶时频谱虽然能有效地描述信号的非平稳特性，但其维数较高，不能直接用于齿轮箱故障诊断。因此，还需要采用其它理论进一步挖掘分数阶时频谱中非线性特征，从而提取有效的特征参数。分形几何理论是处理非线性信号的有力工具，并有研究表明齿轮箱振动信号具有多重分形特性［2，8］。鉴于此，本文引入多重分形理论提取分数阶时频谱的特征参数。典型的多重分形分析方法有小波模极大值法、形态学覆盖法和Q阶矩结构分割函数法（Q-MSPF）等［2，9－10］，其中QMSPF具有理论简单、计算复杂度低等优点。由于基于振动信号分析的齿轮箱故障诊断比较关心的是信号频率随时间的变化情况，而不是信号采集的具体时刻，因此分数阶时频谱的时间和频率信息具有不同的重要性，提取的特征参数应该具有时间平移不变性和频率平移敏感性。若将传统的多重分形分析方法直接应用于分数阶时频谱，所提取的多重分形特征难以满足上述要求。

因此，本文在采用分数阶S变换获取齿轮箱振动信号分数阶时频谱的基础上，针对分数阶时频谱的特点，对Q阶矩结构分割函数法进行改进，提出一种基于Q阶加权矩结构分割函数法的分数阶时频谱多重分形特征提取方法，并对5种状态的齿轮箱振动信号进行了分析和研究。

1 分数阶S变换

1.1 分数阶Fourier变换和S变换简介

分数阶Fourier变换作为Fourier变换的广义形式，可以根据需要将信号从时域变换到不同的分数阶频域，表现出良好的时频旋转特性。信号x（t）的分数阶Fourier变换为［11］

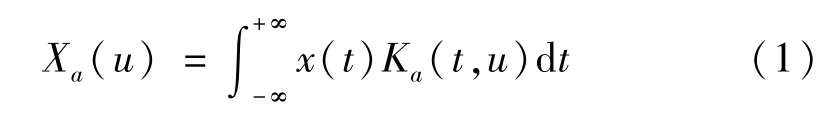
式中，u为分数阶频率；Ka（t，u）为变换核，表达式为

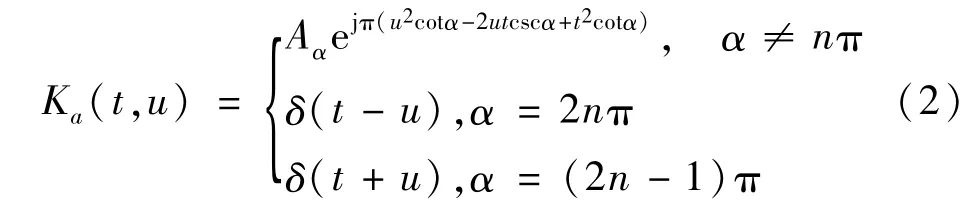
S变换是近年来提出的一种较新的时频分析技术，其时窗宽度随频率增大而减小，因而在低频具有较高的频率分辨率，在高频具有较高的时间分辨率。信号x（t）的S变换为［6］

1.2 分数阶S变换定义

为改善S变换对高频信号的频率分辨率，从而提高S变换整体的时频分辨性能，结合分数阶Fourier变换和S变换，定义分数阶S变换如下

式中，u为分数阶频率；w（τ－t，u）为高斯窗函数，表达式为

式中，p为调整参数，p∈（0，1］。

由式（4）可知，分数阶S变换的时窗宽度随分数阶频率u的变化而改变，因而在分数阶低频具有较高的频率分辨率，在分数阶高频具有较高的时间分辨率，继承了S变换良好的时频分辨性能。随着变换阶次a取值的不同，分数阶S变换能将信号变换到不同的分数阶频域进行时频分析，从而获得最佳的时频分辨性能。当a＝1且p＝1时，分数阶频域即传统的频域，此时分数阶S变换退化为S变换。

2 Q阶加权矩结构分割函数法

2.1 Q阶矩结构分割函数法

Q阶矩结构分割函数法（Q-MSPF）是一种借助统计学中样本矩的概念，通过构造时间序列的结构方程来进行多重分形分析的方法。对于长度为N的时间序列xi，i＝1，2，…，N，Q-MSPF主要包括以下几步［10，12］：

式中，q为实数。如果具有多重分形，Q阶矩结构分割函数满足以下标度特性

式中，τ（q）为质量指数。对于不同的q值，τ（q）可以利用最小二乘拟合的方法求得。如果τ（q）是q的线性函数，则时间序列具有单分形特性；否则，时间序列具有多重分形特性。据此可以判定时间序列是否具有多重分形特性。

（4）按照式（9）对τ（q）进行勒让德变换得到多重分形奇异谱α（q）和多重分形谱f（α）。

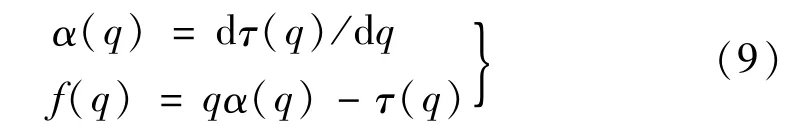
式中，α称为奇异指数。对于复杂的分形体，可以根据奇异指数将其划分为一系列不同的子集。多重分形谱f（α）表示具有相同奇异指数α值的子集分形维数，描述了奇异指数α概率分布情况，是多重分形体不规则和不均匀程度的一种度量。

2.2 频率加权的Q阶加权矩结构分割函数法

由2.1节介绍可知，Q阶矩结构分割函数法很容易从一维信号推广到二维分数阶时频谱。但由Q阶矩结构分割函数法提取的多重分形特征参数具有时间和频率平移不变性，直接应用于分数阶时频谱，不利于齿轮箱故障信号分类和故障诊断。为此，本文提出一种频率加权的Q阶加权矩结构分割函数法（Q-WMSPF）。对于分数阶时频谱FrST（τ，u），Q-WMSPF的主要过程如下：

（2）将FrST′（τ，u）划分成大小为s×s的子区域Dij，并按照公式计算各子区域Dij的概率测度

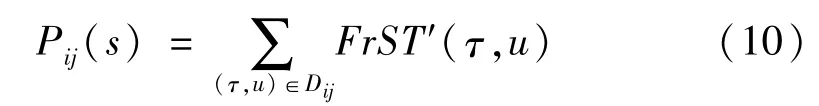
（3）构造频率加权的Q阶加权矩结构分割函数

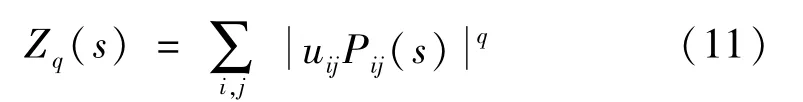
式中，uij为子区域Dij的中心频率。后续步骤同QMSPF，在此不再赘述。由此得到的多重分形奇异谱和多重分形谱分别称为加权多重分形奇异谱和加权多重分形谱。

3 齿轮箱振动信号分析

本文所用齿轮箱振动信号采自于一个二级传动齿轮箱，该齿轮箱由两个直齿轮副组成，齿数分别为18／91和25／50，输入轴的转速为1 491 r／min。试验中模拟并采集了齿轮箱在正常、中间轴齿根裂纹、中间轴齿面磨损、输出轴齿根裂纹和输出轴齿面磨损等5种状态下的振动信号。采样频率和采样长度分别为6 400 Hz和1 024个点。图1为5种状态下采集到的齿轮箱振动信号波形。

图1 齿轮箱振动信号Fig.1 Gearbox vibration signals

3.1 齿轮箱振动信号的分数阶时频谱

对图1中5种齿轮箱振动信号分别进行分数阶S变换，获取分数阶时频谱。对于同种状态的齿轮箱振动信号，变换阶次a和调整参数p取相同值，并且各状态对应的参数取值通过多次实验进行确定。最终，5种信号的分数阶时频谱如图2所示，其中各子图标题后面括号中的数字分别代表参数p和a的取值。

由图2可以看出，不同状态的齿轮箱振动信号的分数阶时频谱具有不同的能量分布，表现出不同的时频特性。由此可知，采用分数阶S变换获取的分数阶时频谱能够有效描述不同状态的齿轮箱振动信号。

图2 齿轮箱振动信号的分数阶时频谱Fig.2 The fractional time-frequency spectrums of gearbox vibration signals

3.2 分数阶时频谱的多重分形特性分析

利用Q-WMSPF研究分数阶时频谱的多重分形特性，要求Q阶加权矩结构分割函数Zq（s）与s具有较好的对数线性关系。图3给出了正常和中间轴齿根裂纹状态下的分数阶时频谱对应的ln Zq（s）～ln s关系曲线，其中各子图从上到下分别为q＝－5，－4，…，4，5对应的ln Zq（s）～ln s关系曲线。

由图3可以看出，对于不同的权重因子q，ln Zq（s）与ln s均呈现出良好的线性关系。因此，可以利用QWMSPF对分数阶时频谱进行研究。

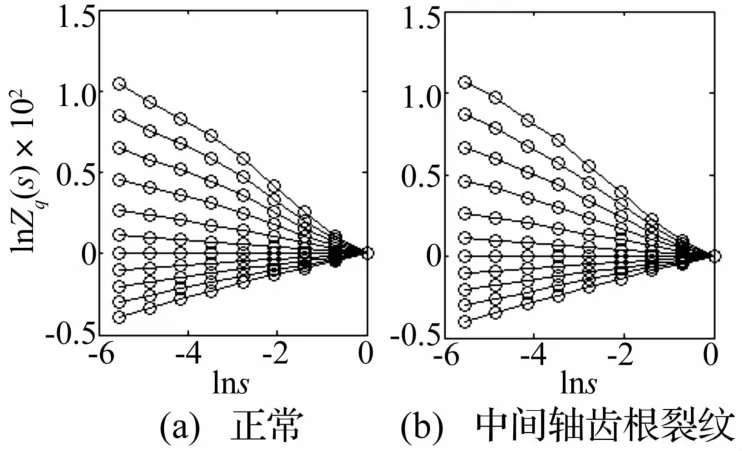
图3 ln Zq（s）～ln s关系曲线Fig.3 The relationship curves of ln Zq（s）～ln s

下面，分别采用Q-WMSPF和Q-MSPF对5种状态齿轮箱振动信号的分数阶时频谱进行研究，结果如图4～图7所示，其中q的取值为－5：0.2：5，每种状态的齿轮箱信号包含3个样本。图4和图6是由Q-WMSPF得到的加权多重分形奇异谱和加权多重分形谱。图5和图7是由Q-MSPF得到的多重分形奇异谱和多重分形谱。

由图4～图7可以看出，随着q绝对值的增大，加权多重分形谱和多重分形谱的谱值均趋于定值，并且在q绝对值较小的范围内，谱值均随着q的增大而迅速减小，呈现出类似于反余切曲线的变化趋势；加权多重分形谱和多重分形谱均随着奇异指数的增大，呈现出倒钩状。由此可知，分数阶时频谱具有多重分形特性，这与齿轮箱振动信号具有多重分形特性是一致的。

图4 加权多重分形奇异谱Fig.4 Weightedmultifractal singular spectrums

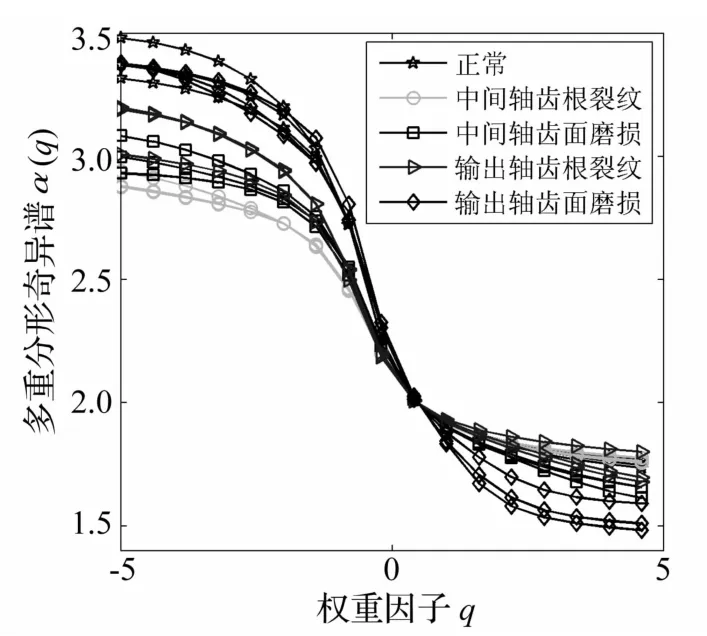
图5 多重分形奇异谱Fig.5 Multifractal singular spectrums

图6 加权多重分形谱Fig.6 Weighted multifractal spectrums

图7 多重分形谱Fig.7 Multifractal spectrums

进一步观察可以发现，与多重分形奇异谱和多重分形谱相比，加权多重分形奇异谱和加权多重分形谱均表现出更好的类间分散性和类内聚合性，尤其在权重因子q较小和奇异指数α较大时对比十分明显。因此，相比于Q-MSPF，由Q-WMSPF得到的多重分形奇异谱和多重分形谱具有更好的可区分性能。

3.3 多重分形特征参数选择及性能分析

由多重分形理论可以形成一套描述多重分形体特征参数集合。常用的多重分形特征参数有αmax、αmin、 Δα、f（αmin）、f（αmax）、Δf和fmax，其中下标max和min分别代表最大值和最小值，Δα＝αmax－αmin，Δf＝f（αmin）－f（αmax）。根据图4～图7中加权多重分形奇异谱和加权多重分形谱的变化情况，本文选择αmax、Δα、f（αmax）和Δf4个参数来描述齿轮箱振动信号分数阶时频谱的多重分形特性。为了便于区分和叙述，称Q-WMSPF提取的特征参数为加权多重分形特征参数。

为研究加权多重分形特征参数的性能，对图2所示的5个分数阶时频谱分别进行0.01 s、0.02 s、0.03 s 和200 Hz、400 Hz、800 Hz的平移处理，然后分别采用Q-WMSPF和Q-MSPF提取以上4个多重分形特征参数，并对各参数进行方差分析。5个分数阶时频谱分析的平均结果见表1。

表1方差分析结果表明：①当分数阶时频谱发生时间平移时，Q-WMSPF和Q-MSPF提取的特征参数波动都比较小，在相同的平移幅度下，加权分形特征参数的波动小于分形特征参数的波动。在允许的误差范围内可以认为两种方法提取的特征参数均具有时间平移不变性，并且加权分多重形特征参数的平移不变性稍好于多重分形特征参数。②当分数阶时频谱发生频率平移时，Q-MSPF提取的特征参数波动很小，而Q-WMSPF提取的特征参数波动非常大，由此可知多重分形特征参数具有近似的频率平移不变性，而加权多重分形特征参数具有频率平移敏感性。

因此，与Q-MSPF相比，Q-WMSPF提取的多重分形特征具有更好的性能。它们受信号采样的开始时刻影响比较小，同时对不同时刻信号能量分布在频率轴上的变化比较敏感，更加有利于齿轮箱振动信号分析和故障诊断。

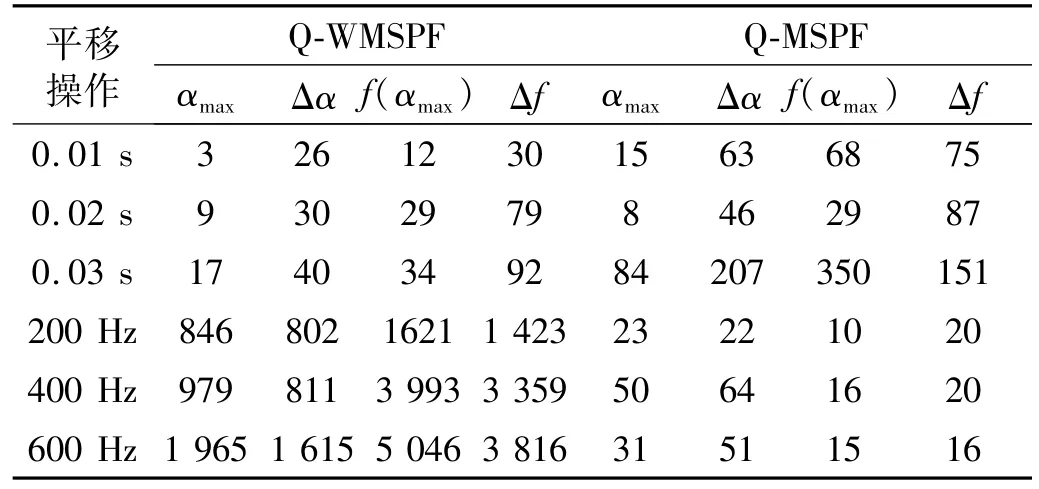
表1 方差分析结果（×10－4）Tab.1 The variance analysis results（×10－4）

3.4 齿轮箱振动信号分数阶时频谱特征提取

从齿轮箱振动信号中随机选取200个样本，每种状态包含40个样本，在利用分数阶S变换得到分数阶时频谱的基础上，分别采用Q-WMSPF和Q-MSPF提取αmax、Δα、f（αmax）和Δf 4个多重分形特征参数。由αmax、Δα和f（αmax）绘制的箱型图见图8，图中不同符号代表不同状态下的齿轮箱振动信号。

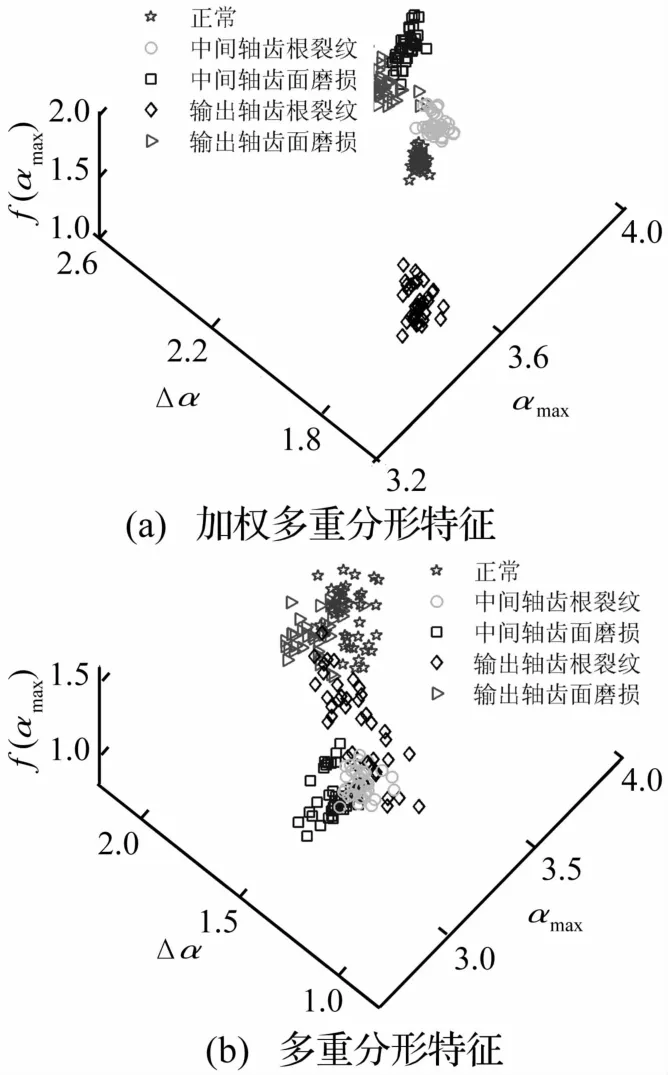
图8 分数阶时频谱特征提取结果Fig.8 Feature extraction results of fractional time-frequency spectrums

从图8可以看出，由于Q-WMSPF通过分数阶时频谱子区域中心频率加权的方式构造了Q阶矩结构函数，所提特征参数具有时间平移不变性和频率平移敏感性，导致加权多重分形特征参数表现出比多重分形特征参数更好的类内聚合性和类间分散性。由此可知，Q-WMSPF提取的多重分形特征参数能更好地描述齿轮箱振动信号的分数阶时频谱的多重分形特征，因而是齿轮箱振动信号的一类新的有效特征参数。

4 结 论

针对非线性、非平稳的齿轮箱振动信号，本文提出了一种基于Q阶加权矩结构分割函数法的分数阶时频谱多重分形特征提取方法。通过构造分数阶S变换获取齿轮箱振动信号的分数阶时频谱，而后采用Q阶加权矩结构分割函数法提取分数阶时频谱的多重分形特征。齿轮箱振动信号研究结果表明：由于分数阶S变换结合了分数阶Fourier变换和S变换的优点，分数阶时频谱可以很好地表达齿轮箱振动信号的时频局部特性；齿轮箱振动信号的分数阶时频谱具有明显的多重分形特性；相比于Q阶矩结构分割函数法，Q阶加权矩结构分割函数法提取的多重分形特征参数具有时间平移不变性和频率平移敏感性，能更有效地描述分数阶时频谱的多重分形特性。

［1］林近山，陈前.基于多重分形去趋势波动分析的齿轮箱故障特征提取方法［J］.振动与冲击，2013，32（2）：97－101.

LIN Jin-shan，CHEN Qian.Fault feature extraction of gearboxes based on multifractal detrended fluctuation analysis ［J］.Journal of Vibration and Sound，2013，32（2）：97－101.

［2］李兵，张培林，米双山，等.齿轮故障信号多重分形维数的形态学计算方法［J］.振动、测试与诊断，2011，31（4）：450－453.

LI Bing，ZHANG Pei-lin，MI Shuang-shan，et al.Mathematicalmorphology based onmultifractal dimensions for gear fault diagnosis［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31（4）：450－453.

［3］迟华山，王红星，郭奇，等.短时傅里叶变换在线性调频信号时频滤波中的应用［J］.电讯技术，2012，52（2）：155－159.

CHI Hua-shan，WANG Hong-xing，GUO Qi，et al.Application of STFT in time-frequency filtering of LFM signals ［J］.Telecommunication Engineering，2012，52（2）：155 －159.

［4］蔡艳平，李艾华，石林锁，等.基于EMD-WVD振动谱时频图像SVM识别的内燃机故障诊断［J］.内燃机工程，2012，33（2）：72－79.

CAIYan-ping，LI Ai-hua，SHI Lin-suo，et al.IC engine fault diagnosis method based on EMD-WVD vibration spectrum time-frequency image recognition by SVM［J］.Chinese Internal Combustion Engine Engineering，2012，33 （2）：72－79.

［5］马伦，康建设，孟妍，等.基于Morlet小波变换的滚动轴承早期故障特征提取研究［J］.仪器仪表学报，2013，34 （4）：920－926.

MA Lun，KANG Jian-she，MENG Yan，et al.Research on feature extraction of rolling bearing incipient faultbased on Morletwavelet transform［J］.Chinese Journal of Scientific Instrument，2013，34（4）：920－926.

［6］Djurovi I，Sejdi E，Jiang J.Frequency-based window width optimization for S-transform［J］.AEU-International Journal of Electronics and Communications，2008，62（4）：245－250.

［7］Ervin S，Igor D，Ljubisa S.Fractional Fourier transform as a signal processing tool：an overview of recent development［J］.Signal Processing，2011，91：1351－1369.

［8］Lin Jin-shan，Chen Qian.Fault diagnosis of rolling bearings based on multifractal detrended fluctuation analysis and Mahalanobis distance criterion［J］.Mechanical Systems and Signal Processing，2013，38：515－533.

［9］Peng Z，Chu F，Tse PW.Singularity analysis of the vibration signals by means of wavelet modulus maximal method［J］.Mechanical Systems and Signal Processing，2007，21（2）：780－794.

［10］Zhang D T，Luo F.A new detectingmethod for weak targets in sea clutter based on multifractal properties［C］／／Proceedings of 2011 IEEE CIE International Conference on Radar，Chendu，2011：446－449.

［11］陶然，邓兵，王越.分数阶傅里叶变换及其应用［M］.北京：清华大学出版社，2009.

［12］孙康，金钢，朱晓华，等.基于Q-MMSPF的海杂波多重分形互相关分析和目标检测［J］.国防科技大学学报，2013，35（3）：170－175.

SUN Kang，JIN Gang，ZHU Xiao-hua，et al.Multifractal cross-correlation analysis of sea clutter and target detection based on Q-MMSPE［J］.Journal of National University of Defense Technology，2013，35（3）：170－175.

M ultifractal feature extraction for fractional time-frequency spectra of gearbox vibration signals

ZHANG Yun-qiang，ZHANG Pei-lin，WU Ding-hai，LIBing

（Department of Vehicle and Electrical Engineering，Ordnance Engineering College，Shijiazhuang 050003，China）

For the nonlinearity and nonstationarity of gearbox vibration signals，a multifractal feature extraction approach for their fractional time-frequency spectra based on a Qth order weighted moment structure partition function method was proposed.A fractional S transformation with better time-frequency resolution was firstly constructed to obtain fractional time-frequency spectra of gearbox vibration signals.Then，aiming at the characteristics of fractional timefrequency spectra，a Qth order weighted moment structure partition function method was designed to extractmultifractal features of the fractional time-frequency spectra.The gearbox vibration signals under five stateswere analyzed.The results indicated that the fractional time-frequency spectra of gearbox vibration signals have the multifractal features，and the extracted multifractal features using the Qth orderweightedmoment structure partition functionmethod canmore effectively describe themultifractal characteristics of fractional time-frequency spectra.

gearbox；time-frequency analysis；multifractal；Qth order weighted moment structure partition function method；fractional S transformation

TH113；TK411

A

10.13465／j.cnki.jvs.2015.21.014

国家自然科学基金资助项目（E51205405，51305454）

2014－06－30 修改稿收到日期：2014－11－06

张云强男，博士生，1987年9月生

张培林男，教授，博士生导师，1955年12月生