基于频域信号的稀疏编码在机械故障诊断中的应用

朱会杰，王新晴，芮 挺，李艳峰，李立平

（1.解放军理工大学野战工程学院，南京 210007；2.总装备部工程兵科研一所，江苏无锡 214035；3.总装备部汽车试验场，安徽定远 233200）

基于频域信号的稀疏编码在机械故障诊断中的应用

朱会杰1，2，王新晴1，芮 挺1，李艳峰1，李立平3

（1.解放军理工大学野战工程学院，南京 210007；2.总装备部工程兵科研一所，江苏无锡 214035；3.总装备部汽车试验场，安徽定远 233200）

提出了一种使用稀疏编码对机械频谱信号自学习并识别故障的方法。首先分别对每类频谱信号进行字典学习得到每类信号的字典，然后依次计算测试样本在各个类别的字典上的稀疏重构系数，利用稀疏重构系数与对应类别的字典重构测试样本。最后将重构残差作为识别依据，对机器状态进行判断。通过将振动信号从时域转化到频域，将复杂的移不变稀疏编码问题转化为普通的稀疏编码，并且得益于高效的K-SVD字典学习算法，计算效率得到了大幅提高。所提方案直接使用原始频谱信号作为训练集，不仅省去了特征提取过程，而且保留了更丰富的信息。经实验验证，该方案较基于时域的移不变稀疏编码具有更高的计算效率、准确率和稳定性。相对于常规诊断算法，除了有准确率的优势外，不易受负载变化的影响，所需人工干预较少。

故障诊断；特征提取；稀疏编码；K-SVD；字典学习

为了实现对运行机械的故障诊断，一般首先对采集的信号提取特征，然后输入到合适的分类器进行故障识别。如何提取反映机器故障状况的特征是故障诊断研究不仅需要耗费大量的时间，而且还要有相关的知识和经验。如果能够直接对原始信号直接训练并分类，通过自主学习实现自动诊断，则能大大降低诊断难度。近些年受到广泛关注的稀疏编码是一种优秀的机器学习方法［1－3］，本文旨在研究如何使用稀疏编码对机械设备进行高效、准确和稳健的自动诊断。稀疏编码将信号表示成基与系数的线性组合，通过字典学习可以自适应地学习到对原信号最优稀疏表示的一组基（即字典）和稀疏系数［3］。往往把求解最优字典的过程叫做字典学习，单独求取稀疏系数则称为稀疏表示。

Wright等［4］提出了稀疏表示分类（Sparse Representation Classification，SRC）方法并用于人脸识别，将分类问题转化为稀疏表示问题，为稀疏表示与模式识别之间建立了桥梁。在SRC中，将所有训练样本合并为一个冗余字典，然后求解测试样本在冗余字典中的稀疏表示，并分别使用各个类别的子字典对测试样本进行重构。将与测试样本具有最小误差的子字典的类别作为测试样本的类别实现分类。但是将所有的训练样本构建成一个冗余字典，导致了冗余字典的规模巨大，稀疏求解时计算量非常大。另外原始训练样本含有噪声等干扰信息也会影响识别率。Yang等［5］基于字典学习提出了一个更高效更稳健的稀疏识别方法——Metaface。Metaface不是按照SRC那样把原始训练样本作为字典，而是分别对每个类的样本学习一组字典，从而减少字典规模以及减少了基的噪声干扰。采用自学习字典的稀疏编码进行模式识别已经在图像处理、姿态识别中得到了广泛的应用［5－7］。

对时域振动信号分析时，需要截取一段信号进行分析，由于截取信号起点的随意性，不能保证同一状态的信号具有相同的特征模式。为了解决特征时移的问题，Liu等［8－11］采用了一种改进的稀疏编码——移不变稀疏编码进行字典学习并应用于轴承故障诊断，苗中华等［11］在Liu研究的基础上使用移不变稀疏编码对轴承的故障特征提取进行了研究。尽管他们取得了较常规方法优异的效果，但移不变稀疏编码比稀疏编码计算量大许多，而且提取的是局部时域特征，在鲁棒性和计算效率方面有待进一步提高。

基于此，本文提出了一种基于频域信号的稀疏编码的故障自动诊断的方法。首先将时域信号转化到频域，解决了特征时移的问题，可以使用常规高效的稀疏编码求解。本文选用高效的K-SVD算法［12］进行字典学习，提高了计算效率。在训练阶段，使用K-SVD算法对每种状态下的训练样本进行字典学习得到每一类的字典。然后分别使用每种状态下的字典依次对未知状态的样本进行重构，并依据重构残差对机器状态进行识别。这种方案直接使用信号的频谱进行学习和分类，不需要人工选择特征。而且原始的频谱信号覆盖了整个频率段，比低维的特征包含更丰富的信息［13－14］，更能体现信号的本质特征，也具有较高的准确率和鲁棒性。

1 基于稀疏编码的故障诊断原理

1.1 基于频谱的模式识别机理

图1 不同状况下的轴承振动时域信号Fig.1 The bearing vibration signals under different status

图2 不同状况下的轴承振动信号包络谱Fig.2 The envelope spectra of bearing vibration signals under different status

对于许多机器设备，当故障发生或者故障位置不同时，会表现出不同的特征频率或规律［15－16］，比如轴承和齿轮。对于同一种状态下的机器，尽管负载会发生变化，但振动频谱仍具有相同的统计规律。图1为四种不同状态下的轴承振动时域信号，图2为所对应的包络谱，每种状态的轴承都分别在负载为1和3马力（HP）下进行测试。可以看出，不同状态下的时域波形具有差异，无法相互稀疏表示。同一状态下的时域波形由于截断的起点不同，波峰所处的位置不同，也无法相互稀疏表示。而不同状态下的频谱差异很大，显然难以使用其他状态下的频谱稀疏表示。而同种状态的频谱比较相似，具有相似的统计规律（由傅里叶变换性质也可推得），可以使用同种状态下的频谱相互稀疏表示。因此，将振动信号转化到频谱后，可以借助于稀疏编码进行表示和分类。

1.2 K-SVD字典学习算法的过程

字典学习能够自动学习到代表原始信号内部结构和主要特征的一组字典，能够使用较少的基表示原始信号，并且对随机噪声不敏感。常用的字典学习方法有最大似然法、MOD（Method of Optima Directions）法、最大后验概率法和K-SVD算法［12］，本文采用高效的KSVD算法。

K-SVD通过字典更新与系数求解两个过程的迭代实现字典学习，它可以与任何追踪方法耦合应用，本文选用OMP（Orthogonal Matching Pursuit）［17］。在系数求解阶段，固定字典不变，使用OMP求解稀疏表示的系数。在字典更新阶段，在更新基的同时，也更新了稀疏系数，进一步加快算法的收敛。下面主要介绍K-SVD字典更新的过程。

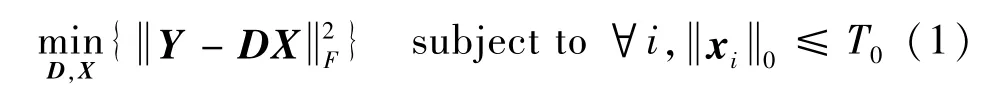
这里T0为稀疏表示中非零分量个数的上限。‖·‖F表示F范数，这里选用2范数。

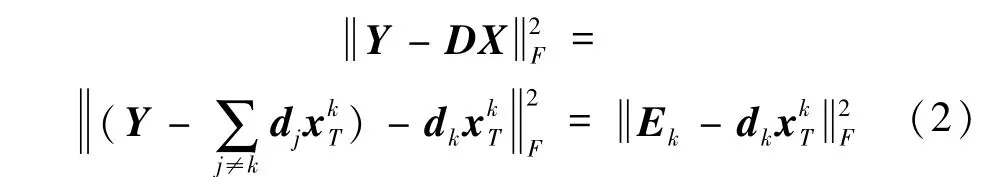
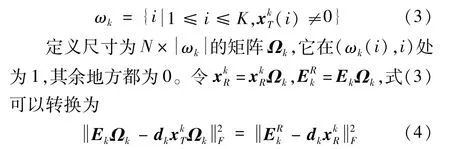
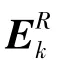
1.3 基于重构残差的机械状态识别原理

按照1.2节的方法，在稀疏度T0下依次对每种状态下的频谱分别进行字典学习得到每一类对应的字典。由K-SVD学习到的每个字典相当于构成了一个单独的空间，原始信号的主要能量能够稀疏地分布于该空间中。尽管不保证学习到的基正交，但这种自学习的基对信号表示的稀疏性远远优于常规的小波基、余弦基等。为了防止各个子字典所构成的空间的相互干扰，本文并没有像Metaface那样将所有子字典合并成一个大的冗余字典，而是单独使用每个子字典依次对测试样本进行稀疏表示。在实际应用中这种方法往往效果更好。

对未知类别的样本进行状态识别的流程如图3所示。假设机器的状态共有n类，那么学习到的子字典也有n个。首先分别在稀疏度T0下使用各个类别的子字典求解该样本的稀疏系数，然后再利用稀疏系数与对应的子字典依次重构测试样本。当子字典的类别与测试样本的类别相同时，该子字典应该能够在稀疏度T0下较好地重构出该测试样本。而当子字典的类别与测试样本的类别不一致时，由于不同状态下的频谱差异较大，很难在稀疏度T0下很好地恢复出该测试样本。也即可以将与测试样本具有最小误差的子字典的类别作为测试样本的类别来实现分类。

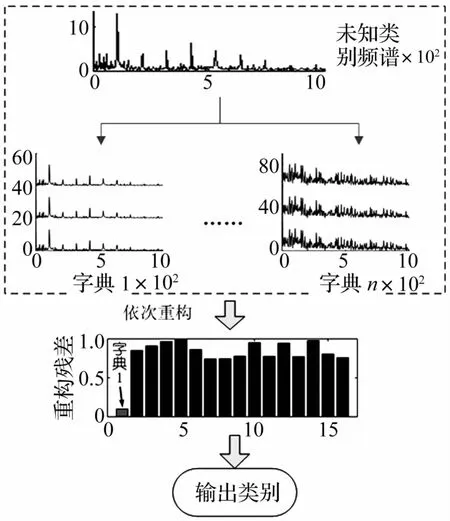
图3 基于重构残差的状态识别流程图Fig.3 The flow chart of pattern recognize based on reconstructed residual

2 基于包络谱的稀疏编码在轴承故障诊断中的应用

为了验证本方案的诊断效果，使用西储大学的轴承数据对轴承的故障类型和故障程度同时进行识别。该试验使用电火花加工技术分别在轴承外圈（3点钟、6点钟、12点钟方向）、内圈、滚动体上布置了单点故障，故障直径分别为0.018、0.036、0.053、0.071 cm，每种状态都分别在负载为0、1、2、3 HP（1 HP＝746 W）的工况下分别测试，信号的采样频率为12 kHz。为了能够同时区分故障类型和故障程度，我们将数据分为16类，每一类数据都包含负载为0、1、2、3 HP四种工况，数据与类别的对应关系见表1。Normal表示正常状态，IR、B与OR分别表示内圈、球和外圈故障，其后的数字代表了故障程度，＠后面表示故障点所处方位。比如，OR014＠3表示轴承有外圈故障，故障直径为0.036 cm，故障点位于3点钟方向。

由于信号是在不同的转速下测试的，为了消除转速的变化对频谱带来的影响，首先对每个信号进行重采样，使得重采样后信号的等价转速为1 750 r／min。重采样之后，将每个信号分割成长度为2 048点且相互之间没有重叠的样本。每个正常状态下的信号大约被分割为118个样本，每个故障状态下的信号大约被分割为59个样本。为了更好地提取冲击特征，使用能量算子对信号进行包络，之后再进行频谱分析。然后使用KSVD分别对每类训练样本进行字典学习，每个子字典包含10个基，稀疏度T0限制为5，最大迭代次数为50次。

表1 数据与类别的对应关系Tab.1 The relationshipof data and labels

图4 学习到的字典中部分基的波形Fig.4 Some bases of learned dictionaries

Liu等［9］曾使用该数据库，首先利用移不变稀疏编码对时域信号学习到不同种类的字典，并将所有种类的字典合并为一个冗余字典。之后使用该冗余字典对测试样本进行稀疏表示，并将稀疏系数作为特征输入到分类器进行识别。为了验证本文方法的优异性，主要做了两个实验，并且训练样本和测试样本的选取与Liu的实验相同。在第一个实验中，随机抽取一半各种状态下负载为0 HP的样本作为训练样本，并从学习到的每类字典中随机挑选3个基画出波形（见图4）。可以看出，基的波形变化很复杂，与小波基、傅里叶基等差别很大，并且不同类别的基的波形有明显的差异。然后将所有负载为0 HP的样本作为测试样本，实验十次的平均结果如图5所示，并与Liu的结果进行了对比。可以看出，本文所提算法的准确率很高。图6为类别OR007＠6的一个测试样本在不同类别的字典上的重构误差，可以看到它在类别2的重构误差明显低于其他类别，可以断定该样本属于第2类。此外，它在类别3、4的误差率也较其他类别低一些，而类别2、3、4都是故障直径为0.018 cm的外圈故障，可见通过重构误差还可以直观地看出该样本与各个类别之间的相关度。由于实际运行中的轴承的负载是变化的，我们希望诊断结果能够不受负载变化的干扰。在第二个实验中，选用所有负载为0 HP的样本进行训练，对所有负载为1、2、3 HP工况下的样本进行测试，重复十次的平均结果如图7所示，也与Liu的结果进行了对比。

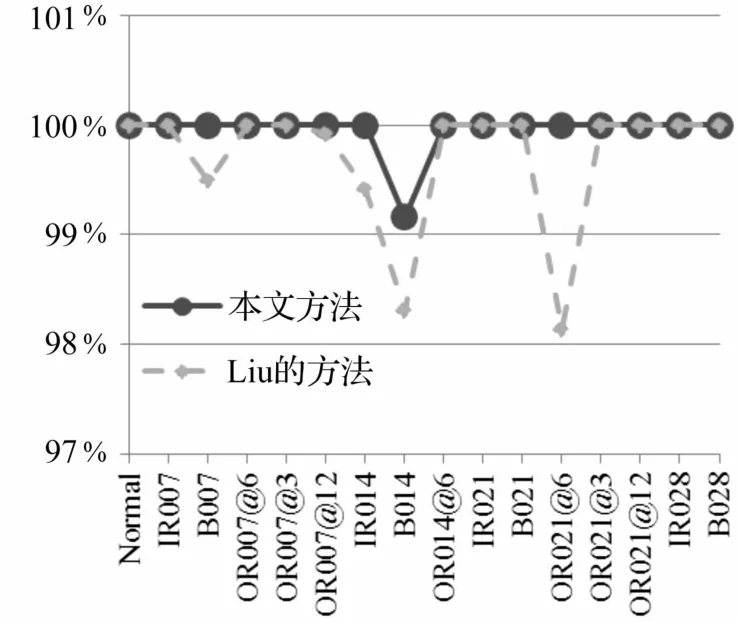
图5 实验一结果对比Fig.5 Comparison with Liu'smethod of experiment1

图6 一个测试样本在各类字典上的重构误差率Fig.6 The reconstructed error ratio in every dictionary of a test sample

图7 实验二结果对比Fig.7 Comparison with Liu'smethod of experiment 2

从方法上来讲，本文方案和Liu的方法都是基于稀疏框架进行故障诊断的。Liu基于时域信号，而本文方案是对频域信号进行训练的，从而解决了特征时移问题，避免了复杂的卷积运算，并选用了高效率的K-SVD字典学习算法，大大提高了计算效率。在主频2.2 GHz 的CPU、内存为2 G的电脑上，使用Liu的方法做完两个实验大约需要20多个小时，而采用本文方法仅需10分钟左右，能够适用于在线监测。此外，Liu的方法借助了分类器，而本文方案没有添加分类器，而是基于重构误差，直接对原始频域信号进行处理。

从实验结果上看，在实验一中两种方法的准确率都很高，其中本文方法略优。这主要是因为训练样本和测试样本都完全取自同一工况，训练样本与测试样本特征很接近。在实验二中，本文方法的优势得到了进一步体现，本文方法的平均准确率明显较高，随着负载的增加优势越明显。而且本文方法性能也更稳定，即使在最差的情况下也有将近80%的准确率，所有状态下的平均准确率为98%。而Liu的方案则不够稳定，在一些工况下准确率只有20%。

为了更加全面反映本文方法的性能，还与近几年其他学者使用西储大学数据的结果进行了对比。Xu等［13］使用EMD和能量熵来提取特征，之后采用粒子群优化的支持向量机对轴承故障进行诊断。他仅选用负载为0 HP下三个信号Normal、IR021、OR021＠6，分为正常、内圈故障与外圈故障三类，训练样本每类选用30个，测试样本每类选用10个，诊断的整体准确率为96%左右。但是他实验中的训练样本和测试样本的负载相同，故障程度也仅有一种情况，比本文实验要简单一些。Shen等［18］采用小波包、距离评价技术和支持向量回归对轴承进行故障诊断。Shen对负载为1 HP下的正常、内圈故障、外圈故障、球故障信号（共分为4个类别，故障直径为0.018 cm）进行状态识别，每类选用30个训练样本和60个测试样本。尽管他实验中的参数选择最好时所得的结果与本方法的平均准确率接近，但他的实验没有考虑负载的变化。与这些方法相比，除了具准确率的优势外，本方案最突出的优点在于直接对信号频谱进行训练和识别，不需要人工提取特征，减少了工作量且不易受人工经验的影响。另外，得益于稀疏编码良好的鲁棒性，能够在训练样本与测试样本的负载不同的情况下仍然能够以较高的准确率对轴承进行诊断。

3 结 论

本文提出了一种采用稀疏编码对机械频域信号进行自学习与故障诊断的方案。使用机械频域信号进行字典学习解决了时域信号特征的时移性，不需要使用复杂的移不变稀疏编码，而且得益于高效的K-SVD字典学习算法，能够快速地学习到每类训练样本的字典。相对于Liu的基于时域的移不变稀疏编码诊断方法，本方案将计算效率提高了约100倍，而且诊断的鲁棒性有所提高。与常规方法相比，本方案的优势不仅仅在于高准确率，而且得益于稀疏编码对高斯噪声的免疫性和良好的自适应性，能够不受负载的变化实现对机器的准确诊断。尽管本方案的计算量相对于常规算法并没有显著减小甚至有所增加，但节省了人工提取特征的时间和工作，能够实现自动学习和诊断，因此计算量的增加是值得的。

［1］Olshausen B A.Emergence of simple-cell receptive field properties by learning a sparse code for natural images［J］.Nature，1996，381（6583）：607－609.

［2］Candès E J，Wakin M B.An introduction to compressive sampling［J］.Signal Processing Magazine，IEEE，2008，25 （2）：21－30.

［3］宋长新，马克，秦川，等.结合稀疏编码和空间约束的红外图像聚类分割研究［J］.物理学报，2013，62（4）：77－86.SONG Chang-xin，MA Ke，QIN Chuan，et al.Infrared image segmentation based on clustering combined with sparse coding and spatial constraints［J］.Acta Physica Sinica，2013，62 （4）：77－86.

［4］Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，2009，31 （2）：210－227.

［5］Yang M，Zhang L，Yang J，et al.Metaface learning for sparse representation based face recognition［C］／／Image Processing，IEEE International Conference on，IEEE，2010：1601－1604.

［6］孙俊，王文渊，卓晴.基于稀疏编码的提取人脸整体特征算法［J］.清华大学学报：自然科学版，2002，42（3）：411－413.

SUN Jun，WANG Wen-yuan，ZHUO Qing.Sparse codingbased global face feature extraction algorithm［J］.Journal of Tsinghua University：Science and Technology，2002，42（3）：411－413.

［7］肖玲，李仁发，曾凡仔，等.基于自学习稀疏表示的动态手势识别方法［J］.通信学报，2013，34（6）：128－135.

XIAO Ling，LI Ren-fa，ZENG Fan-zai，et al.Gesture recognition approach based on learning sparse representation ［J］.Journal on Communications，2013，34（6）：128－135.

［8］Grosse R，Raina R，Kwong H，et al.Shift-invariance sparse coding for audio classification［C］／／Ron Parr，Linda van der Gaag.Conference on Uncertainty in AI，Vancouver：AUAI Press，2007：149－158.

［9］Liu H，Liu C，Huang Y.Adaptive feature extraction using sparse coding for machinery fault diagnosis［J］.Mechanical Systems and Signal Processing，2011，25（2）：558－574.

［10］Smith E C，Lewicki M S.Efficient auditory coding［J］.Nature，2006，439（7079）：978－982.

［11］苗中华，周广兴，刘海宁，等.基于稀疏编码的振动信号特征提取算法与实验研究［J］.振动与冲击，2014，33 （15）：76－81.

MIAO Zhong-hua，ZHOU Guang-xing，LIU Hai-ning，et al.Tests and feature extraction algorithm of vibration signals based on sparse coding［J］.Journal of Vibration and Shock，2014，33（15）：76－81.

［12］Aharon M，Elad M，Bruckstein A.K-SVD：an algorithm for designing overcomplete dictionaries for sparse representation ［J］.Signal Processing，IEEE Transactions on，2006，54（11）：4311－4322.

［13］Xu H，Chen G.An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO ［J］.Mechanical Systems and Signal Processing，2013，35 （1）：167－175.

［14］Bin G，Gao J，Li X，et al.Early fault diagnosis of rotating machinery based on wavelet packets－empirical mode decomposition feature extraction and neural network［J］.Mechanical Systems and Signal Processing，2012，27：696－711.

［15］Randall R B，Antoni J.Rolling element bearing diagnostics －a tutorial［J］.Mechanical Systems and Signal Processing，2011，25（2）：485－520.

［16］Lei Y，He Z，Zi Y.A new approach to intelligent fault diagnosis of rotating machinery［J］.Expert Systems with Applications，2008，35（4）：1593－1600.

［17］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.Information Theory，IEEE Transactions on，2007，53（12）：4655－4666.

［18］Shen C，Wang D，Kong F，et al.Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier［J］.Measurement，2013，46（4）：1551－1564.

Application of sparse coding based on frequency domain signals in machinery fault diagnosis

ZHU Hui-jie1，2，WANG Xin-qing1，RUITing1，LIYan-feng1，LILi-ping3

（1.College of Field Engineering，PLA University of Science and Technology，Nanjing 210007，China；2.The First Engineering Scientific Research Institute of General Armaments Department，Wuxi214035，China；
3.Automotive Proving Group of the General Armament，People's Liberation Army）

An automatic learning and recognition scheme using sparse coding based on freqency domain signalswas proposed here.Firstly，each dictionary for per class of frequency domain signals was obtained with a dictionary learning algorithm.Later，the test sampleswere sparselyly represented，respectively using the dictionaries of each class to calculate corresponding sparse reconstruction coefficients.Afterwards，the dictionaries with corresponding coefficients of the same class were applied to reconstruct the test samples.Finally，the reconstructed residual was taken as the criterion to determinemachine states.Through converting vibration signals in time domain into those in frequency domain，a complex shift-invariant sparse coding problem，was simplified as an ordinary sparse coding one，and with the help of the effective K-SVD algorithm，the whole efficiency was further significantly improved.The original spectra singalswere directly used as training samples in the proposed scheme，so that the complicated feature extraction was not needed，and more information was reserved.The test verification showed that the proposed technique improves greatly the efficiency and robustness compared to the shift invariant sparse coding in time-domain；compared with the traditional algorithms，besides the advantage of accuracy，this proposed scheme needs less cost and is affected less by load variation.

fault diagnosis；feature extraction；sparse coding；K-SVD；dictionary learning

TN165.3

A

10.13465／j.cnki.jvs.2015.21.011

国家自然科学基金项目（61472444，61472392）

2014－06－11 修改稿收到日期：2014－10－23

朱会杰男，博士，工程师，1987年1月生

芮挺男，副教授，1975年3月生