基于模糊粗糙集的气象因子与森林火灾相关性研究

（中南林业科技大学 理学院，湖南 长沙 410004）

森林火灾是一种破坏性极大的自然灾害，不仅破坏绿化成果，危及人民生命和财产安全，同时也影响到国民经济和生态环境建设的健康稳步发展[1-2]。近年来，全球气候变化明显，林火与气候变化逐渐成为林火研究领域的热点问题[3-5]。在以往的研究中，大部分学者都认为水分、温度和风速是影响林火发生的3个主要气象因子[6-8]，但具体哪个因子影响较大却很少有学者对其进行研究。模糊粗糙集模型具有处理不确定性、不完备性信息的能力，及以数据为驱动、不受专家知识制约的特点[9]，其对各属性重要程度排序的能力已在商业[10]、能源[11]等领域得到应用。森林火灾具有成因复杂，发生不确定性的特点，这与模糊粗糙集模型擅长处理的数据类型一致。本研究将运用模糊粗糙集方法对影响森林火灾发生的各气象因子进行重要程度排序，以期为森林火灾的预测、预防提供决策基础。

1 模糊粗糙集理论

粗糙集理论是波兰数学家Pawlak于1982年提出的一种有效的、新的数据处理方法。粗糙集常用于对数据进行属性简约和分类，也可利用属性依赖度求取条件属性对决策属性的重要程度。但粗糙集理论不适用于连续属性值的数据，前人将模糊集引入粗糙集理论中，解决了这一问题，形成了模糊粗糙集理论。模糊粗糙集能最大程度的保留原始数据信息，避免了数据离散化过程中带来的信息丢失问题，使结果更为准确、客观。

定义1 设(U，R)为Pawlak近似空间，R为论域U上的一个模糊等价关系，若X∈U，则X关于R的下近似集和上近似集的隶属函数分别为：

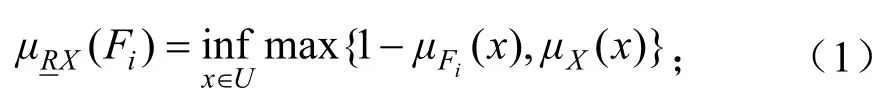
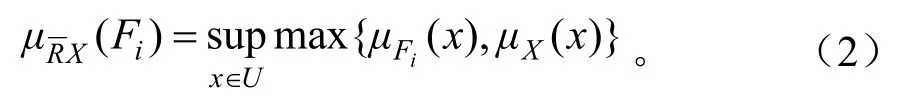
定义2 对于 ∀x∈U，x对模糊正域的隶属度可定义如下：

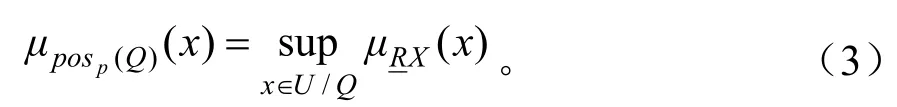
定义3 决策属性Q对条件属性P的依赖度为：

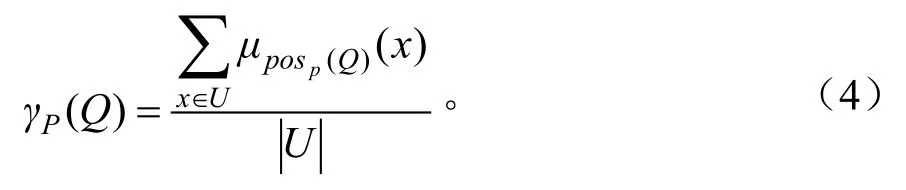
2 数据来源与处理

2.1 气象因子的选择

通过对比前人研究所选因子和数据可获取性原则，本研究选取气象因子中气温、降水量、湿度、风速4个大部分学者都认可的与森林火灾发生相关性较大的因子来研究气象因子与森林火灾的相关关系。

2.2 数据来源

本研究火灾研究区域为湖南省，火灾数据来源于中国森林防火网（www.slfh.gov.cn/slfhw/default.aspx）；气象数据来源于历史气象查询网站（www.rp5.ru）。

2.3 数据收集

（1）随机抽取中国森林防火网上记录的湖南地区历年发生的森林火灾。

具体抽样规则如下：对湖南省每个县、区随机抽取12条森林火灾数据，如某个区、县记录的森林火灾数据不到12条，就抽取该县、区所有已记录的数据，每条数据记录其火灾发生时间、发生地点、起火原因、温度、湿度、风速、降水量等7个属性，共采集数据1 041条。

比对中国森林防火网记录的火灾发生时火灾发生地的气象数据，发现其有较多错误，故用历史气象查询网站的数据予以核验，气象数据中气温为地面以上2 m处的大气温度（℃）、湿度为地面以上2 m处的相对湿度（%）、风速为观测前10 min内地面高度10～12 m处平均风速（m/s）、降水量为森林火灾发生前24 T累计降水量（mm）。

2.4 数据标准化

本研究数据涉及气温、湿度、风速、降水量多个因子，因为火灾发生有一定偶然性及各因子度量单位不同，为提高模型的精确性，本研究先对数据进行标准化处理（因子值减去其平均值后除以其标准差）。

2.5 数据聚类

在模糊粗糙集模型中，决策表由条件属性和决策属性构成，本研究研究的森林火灾气象因子信息决策表中，条件属性指与森林火灾相关的各气象因子，但决策属性在已有数据中无法提取。本研究参照文献[12]，先对气象数据进行聚类，然后处理聚类后的数据得出决策表。本研究采取K-均值聚类算法将所收集的数据聚为24类（取小于的且为年月份数12的最大公倍数24作为K值）。

2.6 决策属性等级划分

在模糊粗糙集模型的信息决策表中，决策属性的值必须是一组离散值，本研究将聚类后每类气象因子的案例数用自然断点法分为低、中、高、特高4级，分级结果见图1。

2.7 组成决策表

把上述步骤中气象因子的最终聚类中心作为条件属性，用自然断点法生成的分级标准将聚类后各类的案例数分成对应等级，并依次用1、2、3、4表示，以此作为森林火灾气象因子决策信息表中的决策属性值。最后组成的决策见表1。

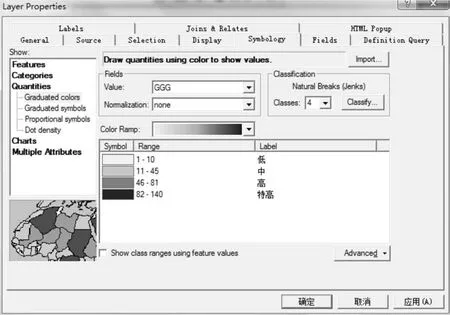
图1 决策属性分级Fig.1 Classi fication of decision attribute

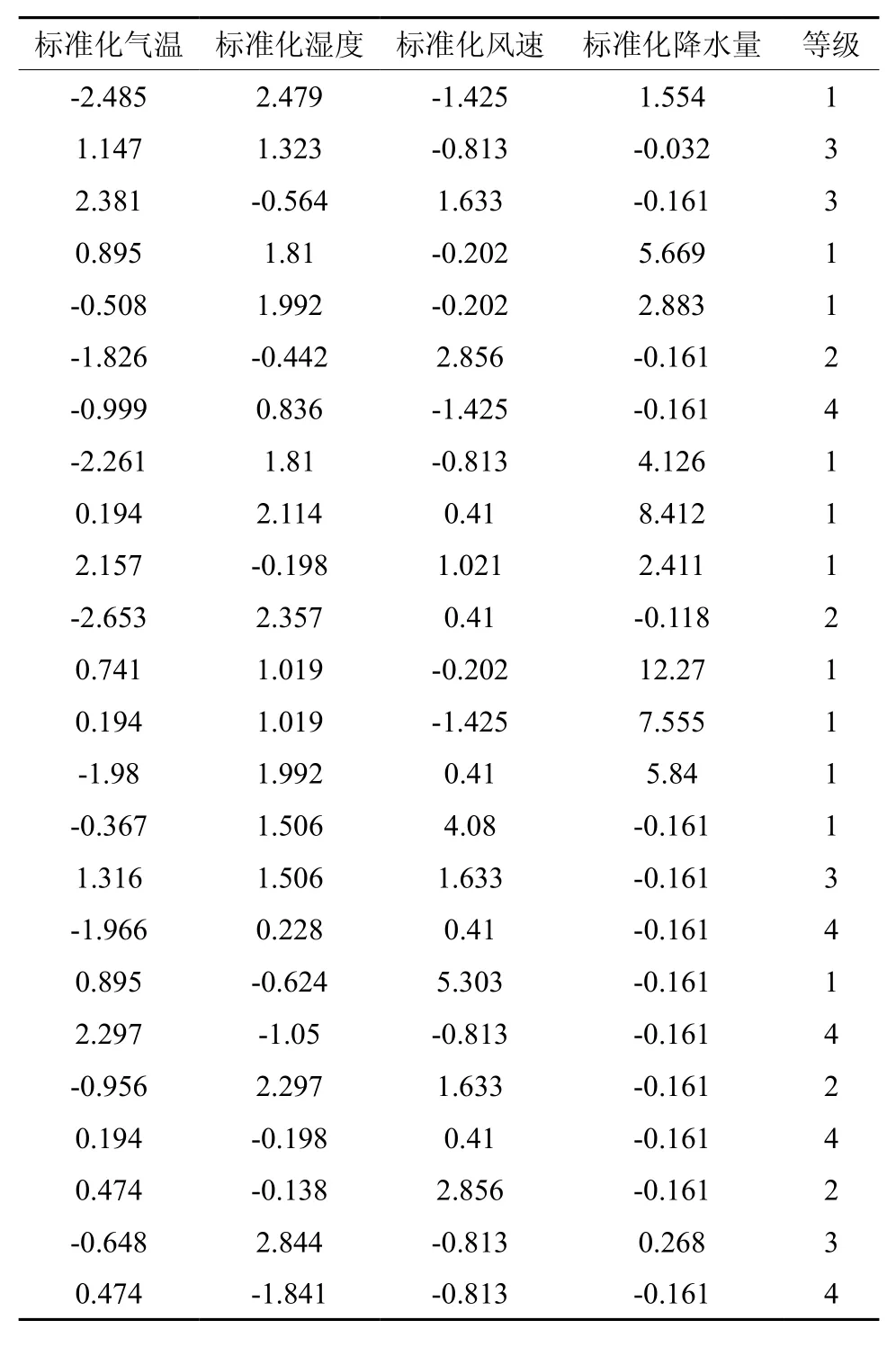
表 1 森林火灾气象因子决策信息Table 1 Decision-making information of forest fire meteorological factors

3 气象因子对森林火灾发生的影响值求取

3.1 模糊化处理

将属性信息决策表中的“标准化气温”、“标准化湿度”、“标准化风速”、“标准化降水量”4个因子分别按升序排列，以每列第3个（总记录条数的15%）和第22个（总记录条数的85%）作为分界点，分为低（L）、中（M）、高（H）3个等级，划分后按三角隶属函数规则构造各属性模糊函数如图2。

将表1中的数据按各属性的模糊隶属函数模糊化后得到结果如表2：

3.2 条件属性依赖度求取

为方便表达与计算，把标准化气温、标准化湿度、标准化风速、标准化降水量4个条件属性分别用字母A、B、C、E表示，决策属性用字母D表示。结合表2所示数据，通过以下步骤求取各条件属性依赖度。

3.2.1 模糊等价类划分

本研究决策属性有低（1）、中（2）、高（3）、特高（4）4个值，因此可据此划分以下等价类：U/D={X1，X2，X3，X4}。

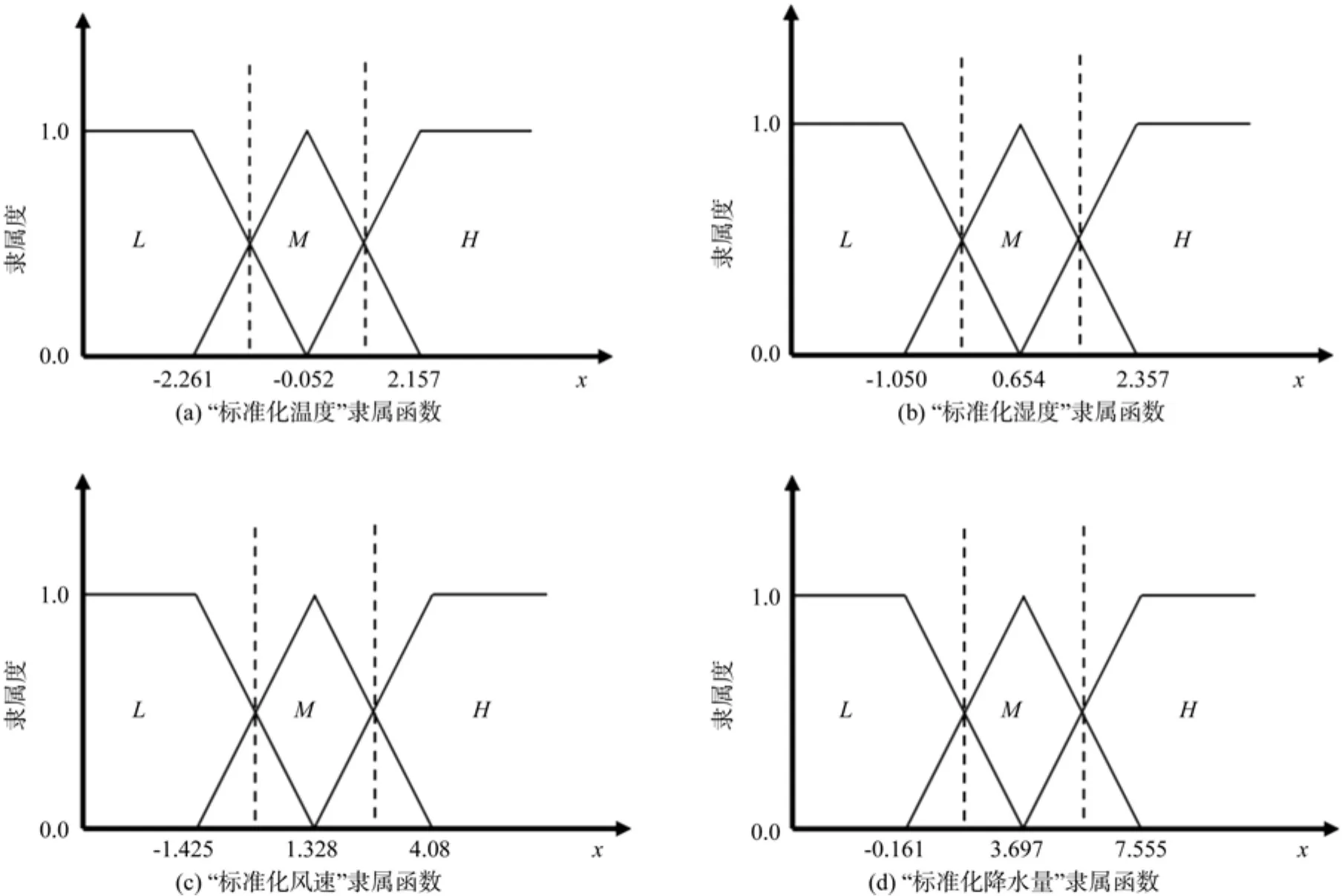
图2 属性隶属度函数Fig.2 Attribute membership functions

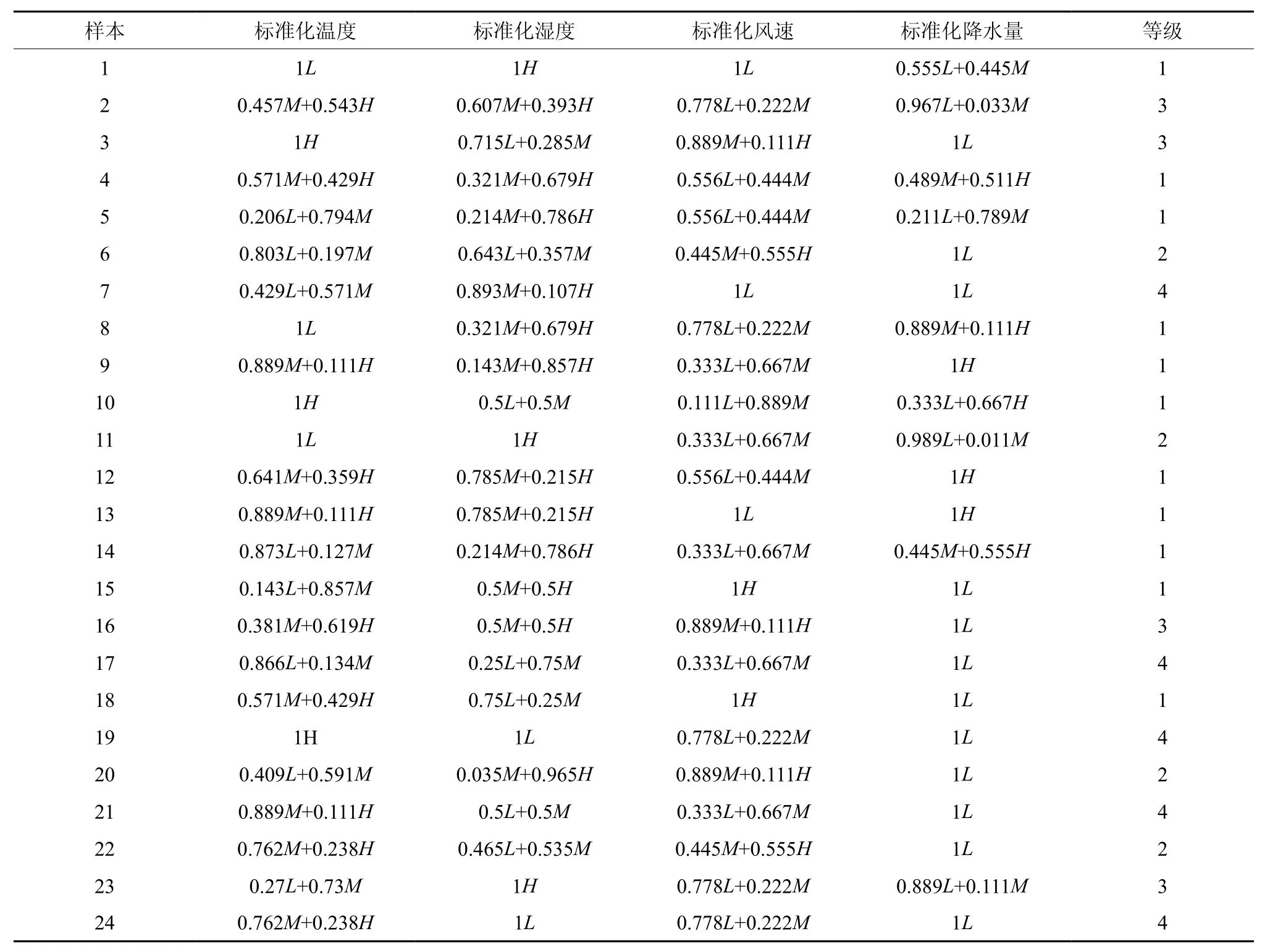
表 2 模糊决策Table 2 Fuzzy decision-making variables

X1={1，4，5，8，9，10，12，13，14，15，18}表示低灾情等级对象集合；

X2={6，11，20，22}表示中灾情等级对象集合；

X3={2，3，16，23}表示高灾情等级对象集合；

X4={7，17，19，21，24}表示特高灾情等级对象集合。

在3.1中，各条件属性都被模糊化为低（L）、中（M）、高（H）三个区间，据此可以划分如下模糊等价类：

U/A={LA，MA，HA}，U/B={LB，MB，HB}，U/C={LC，MC，HC}，U/E={LE，ME，HE}

3.2.2 条件属性下近似集求取

根据定义1，计算各条件属性下近似集，例如，考虑等价类：X1={1，4，5，8，9，10，12，13，14，15，18}，属性A，有：

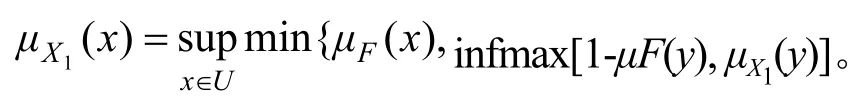
以对象1为例，对于属性集A，等价类X1，可作如下计算：

μX1(LA)=min[1,inf(1,1,1,1,1,0.196 9,……,0.590 8,1,1,0.730 2,1)]=0；

μX1(MA)=min[0,inf(1,0.542 8,1,1,1,……,0.409 2,0.111 4, 0.238 1,0.269 8,0.238 1)]=0；

μX1(HA)=min[0,inf(1,0.457 2,0,1,1,……,0.888 6,0.761 9,1,0.761 9)]=0。

同 理， 可 计 算 求 出μX2(1)=0，μX3(1)=0，μX4(1)=0。

3.2.3 模糊正域隶属度求取

根据定义2，求得属性A，对象1对于模糊正域的隶属度为：

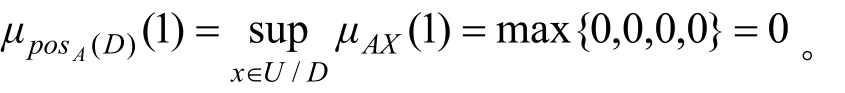
即μposA(D)(1)=0。同理可求得其他对象属性A模糊正域的隶属度，以下仅例出部分结果：μposA(D)(2)=0.111 4，μposA(D)(8)=0，μposA(D)(18)=0.111 4。

3.2.4 属性依赖度求取

根据定义3，可计算属性A相对于决策属性D的依赖度：

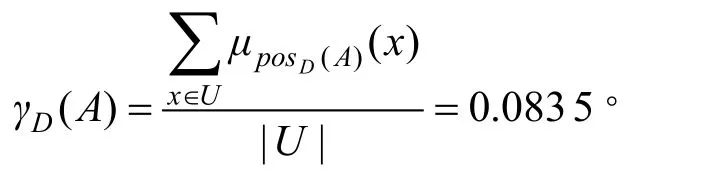
同理，可通过上述步骤求出其他条件属性对决策属性D的依赖度：

γD(B)=0.190 6，γD(C)=0.152 7，γD(E)=0.292 1。

3.3 各气象因子对森林火灾发生影响值求取

将各条件属性对决策属性的依赖度进行归一化处理，得出各属性对森林火灾发生的影响值。归一化公式如下：

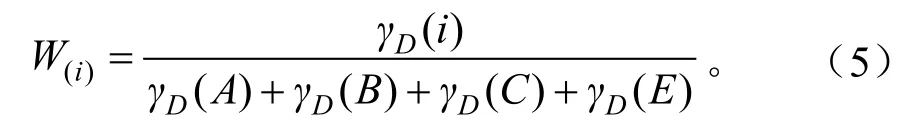
影响值计算结果为：

[W(A)，W(B)，W(C)，W(E)]=(0.116 2,0.265,0.212 4,0.406 3)。

4 对比分析

由于本研究统计的火灾数据为发生火灾时刻的气象数据，一个地区的常年时刻气象数据的提法既不科学，也难实现。考虑到两者对比的可操作性，本研究将发生火灾时的气象因子平均值与该地区常年气象因子平均值作比，将该比值称为该气象因子的灾均比（ZJB），用字母Z表示。分析全文数据，笔者认为气象因子灾均比可以反映出气象因子与森林火灾发生间相关性的正负（Z＞1为正相关，Z＜1为负相关）并能基本反映出气象因子对森林火灾发生的影响程度（与1接近的程度），以此来印证研究结论的正确性。

通过查询历史气象网站，统计了湖南省各地级市的各气象因子常年平均值，再用各地级市的土地总面积加权，得出湖南省各气象因子常年均值。整理后常年均值、火灾时均值及灾均比结果如表3。

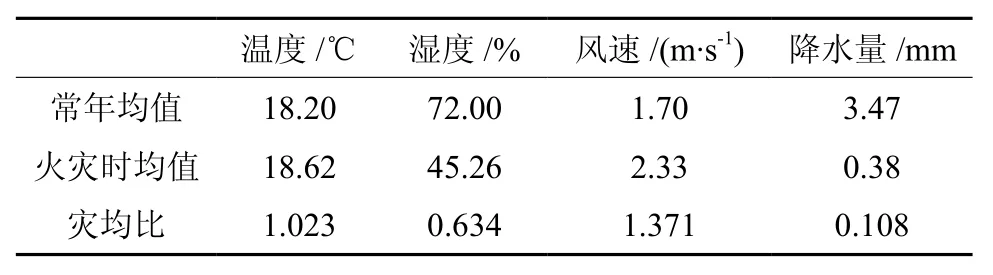
表 3 气象因子平均值统计Table 3 Average values of meteorological factor statistics

在表3中，灾均比大于1的气象因子有温度、风速，小于1的有湿度、降水量，根据前文定义，即温度和风速因子与森林火灾的发生呈正相关关系，湿度和降水量因子与森林火灾的发生呈负相关关系，这与多数学者的研究结论[13]相一致。分析灾均比结果（与1接近的程度）显示，以上4个气象因子中对森林火灾发生影响程度最大的是降水量，其次为温度和湿度，影响最小的为温度因子，这与模糊粗糙集模型得出的结论相一致，从而印证了上文研究结果。

5 结论与讨论

（1）温度、相对湿度、风速和降水量 4 个气象因子中，温度和风速因子与森林火灾的发生呈正相关关系，相对湿度与降水量因子与森林火灾的发生呈负相关关系，相关性最大的因子为本时刻前24小时内降水量，相关程度从大到小依次为：降水量0.406 3、相对湿度0.265 0、风速0.212 4、温度0.116 2。

（2）在运用模糊粗糙集确定各气象因子对森林火灾影响程度的过程中有以下3方面需要做进一步研究，一是K-值聚类算法的K值及初始聚类中心的确定；二是各气象因子模糊化过程中隶属函数的构造；三是文中所用数据为湖南省数据，结论是否能在其他省或地区推广还有待验证。

[1] 孙玉荣,张 贵,陈爱斌,等.湖南森林火灾的灾情区域分异研究[J].中南林业科技大学学报, 2012 ,32(8):7-11.

[2] 储昌超,张 贵,孙玉荣.基于克里金方法的湖南森林火灾趋势预测研究[J].中南林业科技大学学报,2014,34 (6):66-70.

[3] 田晓瑞,舒立福,王明玉,等.林火与气候变化研究进展[J].世界林业研究,2006,19(5):38-42.

[4] 傅泽强,陈 动,王玉彬.大兴安岭森林火灾与气象条件的相互关系[J].东北林业大学学报,2001,29(1):12-15.

[5] 郑焕能,邸雪颖,姚树人.中国林火[M].哈尔滨:东北林业大学出皈社,1993.

[6] 王淑华,孙鹏飞,程春香.伊春市气象因子与森林火灾相关性研究[J].林业科技,2008,33(2):24-26.

[7] 杜毓龙,雷崇典.陕北春季森林火灾气象条件分析[J].气象科学,2006,(3):341-345.

[8] 袁 春.新余市森林火灾气象要素分析[J].江西林业科技,2000, (6):16-18.

[9] Pawlak Z,Wong S,Ziarko W.Rough sets: probabilistic versus deterministic approach ［J］.International Journal of Man-Machine Studies,1988,29(1):81-95．

[10] 应可福,薛恒新.基于重要性的顾客满意度指数的测评[J].商业研究,2005,22:1-4.

[11] 栗 然,曹 磊,李 莉,等.影响电力系统短期负荷预测因素的权重分析方法[J].华北电力大学学报,2007,34(5):32-37．

[12] 曲智林,胡海清.基于气象因子的森林火灾面积预测模型[J].应用生态学报,2007,18(12):2705-2709.

[13] 周昆明,王永平,高月忠.气象因子对大理森林火灾的影响[J].四川林业科技,2012,33(6):96-99.