季节和降雨对细小可燃物含水率预测模型精度的影响

（东北林业大学 林学院，黑龙江 哈尔滨 150040）

林内地表细小可燃物对林火等级划分影响很大，在林火预测预报的工作中，先决条件是必须可以准确地预测可燃物含水率，地表细小可燃物含水率对林火行为也有重要影响[1-6]，地表细小可燃物的含水率预测应用较广的为气象要素回归法[7]，其结构简单，应用广。在1920年左右，美国已经开展了可燃物含水率和气象因子间联系的研究。Weidman[8]将林内可燃物、温湿度及林火联系，提出森林火险预报应该考虑天气和可燃物状态。Gisborne[9]使用实验站资料，将不同环境和含水率的的变化做了研究。

国内对地表细小可燃物含水率预测的研究也有很多成效。卢欣艳等[10]在北京西山建立5种林型观测点，分析了北京西山林场可燃物含水率和气象要素间的关系。王瑞君等[3]在野外进行点火，划分了火险等级。张大明等[11]通过在长白山定位点的气象数据，建立可燃物含水率关系模型。高永刚等[12]通过野外实验，得到五营林场的含水率变化方程。王金叶等[13]研究了祁连山地区的含水率与气象间的相关性。覃先林等[14]对东北地区的典型树种落叶松Larix gmelinii、白桦Betula platyphylla和柞树Xylosma racemosum的可燃物含水率变化进行了测定研究，建立了两者间的回归模型。张国防等人[15]在杉木Cunninghamia lanceolata人工林内进行实验，得到杉木林中的地表可燃物和含水率的关系模型。

以往人们的研究主要是集中在选择合适的气象因子，并没有将季节变化等作为影响因子。但是，地表细小可燃物的含水率预测精度受季节和降雨的影响很大。春秋季林内可燃物失水和吸水就有明显差别，春季由于可燃物都为前一年的，所以失水和吸水的速度大；秋季时由于可燃物为当年落下的，水分变化对环境的响应要慢些。降雨有无则影响可燃物的失水方式。因而，可燃物含水率预测模型按照季节、降雨等因素建立，可能提高其预测精度。本研究以我国大兴安岭盘古林场3种主要林型的细小可燃物为对象，在不同季节和有无降雨的条件下建立预测模型，分析模型精度，为以后的研究提供数据基础。

1 研究地区与研究方法

1.1 研究区概况

本实验的研究区位于我国大兴安岭盘古林场（52°41′57.1″N，123°51′56.5″E），该地区主要是低山山地，包括少量中山。年平均气温为-5 ℃，最低为-52.3 ℃，最高为39 ℃。年降水量350～500 mm，在7～8月份降水多，湿度在70%～75%间。

1.2 研究方法

为使数据更加符合森林防火的需求，因而在2010年5月29日～6月27日（春防期内）和2010年9月23日～10月13日（秋防期内）进行实验。因为阳坡的太阳辐射强，因此在3种林型的阳坡坡位处，建立20 m×20 m的标准地，并以郁闭度为分类条件，分别在林荫下、半遮荫、无遮荫处放置3个样框，为防止称量时框内质量发生变化，用8目尼龙网包裹在框的四周。方筛中放入采集的没有被破坏的凋落物层，并放置在取样处，每天下午14时用电子天平测定其质量。最后将每个方筛中的可燃物放入烘箱内，于105 ℃下烘干一定时间，直至其质量不再变化为止。樟子松林、兴安落叶松林和白桦林的样地基本情况如下表1。每个样地的含水率为3个样点的含水率的算术平均值。含水率计算公式为：

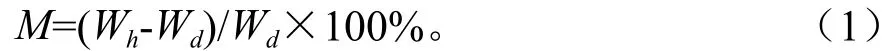
式（1）中：M表示可燃物含水率（%）；Wh表示可燃物湿重（g）；Wd表示可燃物干重（g）。

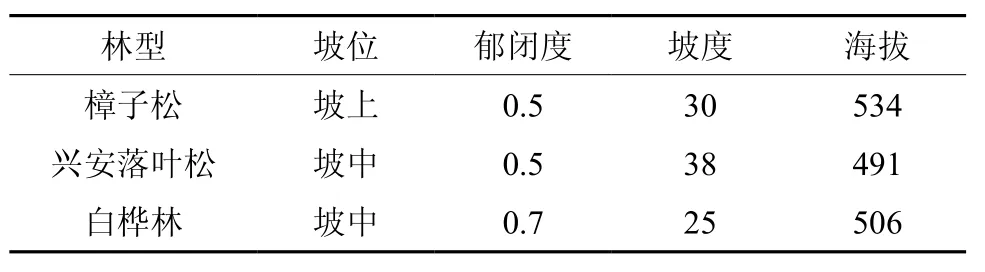
表 1 样地信息Table 1 Information of sampling plots

气象数据是从盘古气象站获取，包括每小时温湿度、降雨量、风速等。主要计算前1～5天的气象因子、1～5天前当日气象因子、前1 天、前2天和前3天的降水量之和等，气象因子获取以每日0点为基准，降水量获取以采样当天14时为基准。将前几天气象因子设为a、几天前当日气象因子设为b，前24 m（m=1～3）小时降水量之和设为c，例如：前2 天降水量之和记为Rc2，前4天平均相对湿度记为Ha4，5天前当日平均温度记为Tb5，前48 T降水量之和记为Rc2。

统计得到，春季防火期内数据共30组，秋季防火期内数据20组，春-秋季数据一共为50组；无降雨期数据31组，降雨期数据19组，混和降雨期数据50组。无降雨期为14:00时前24 T没有降雨的数据；降雨期为下午14:00时前24 T的有降雨数据；混和降雨期为无降雨和降雨期混合数据。

用逐步回归建立死可燃物含水率的多元线性模型：

式（2）中：M为可燃物含水率（%）；bi为待估计参数。

n-Fold交叉验证的可以计算模型精度，对于某个样地的n个数据，用n-1个含水率数据和气象要素进行逐步回归，建立多元线性模型，然后用剩余未参与建立模型的一个数据验证，计算含水率预测模型的误差，可以进行n次验证。误差包括MAE和MRE，公式分别为（3）和（4）式。

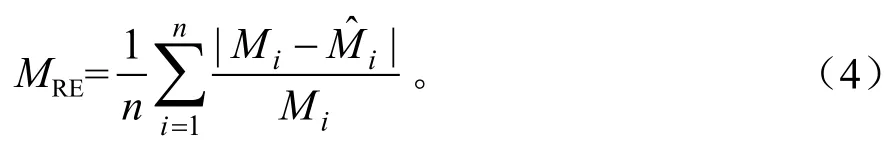
式（3）和（4）中：Mi为含水率实测值（%）；为含水率预测值（%）。

1.3 数据处理

采用SPSS19.0和Excel2013进行数据整理、分析及绘图。

2 结果分析

2.1 样地可燃物含水率动态变化

根据图1可以看出可燃物含水率的变化趋势与前48小时2 天的降水量之和变化趋势最相似。当前2 天降水量之和过高且日最高温度较低时，可燃物含水率明显高于其他情况，可燃物含水率和降水量大时，温度则较低，如采样时序点在9、15、24、53、68等。温度较高时，降水量和可燃物含水率都较低，如采样时序点在8、14、28、48。秋季可燃物含水率要比春季高些，这是因为秋季植物停止生长不久，体内仍有部分水分，并且降雨量大于春季，而春季相对湿度低，地表凋落物含水率为该年中最低[16]。

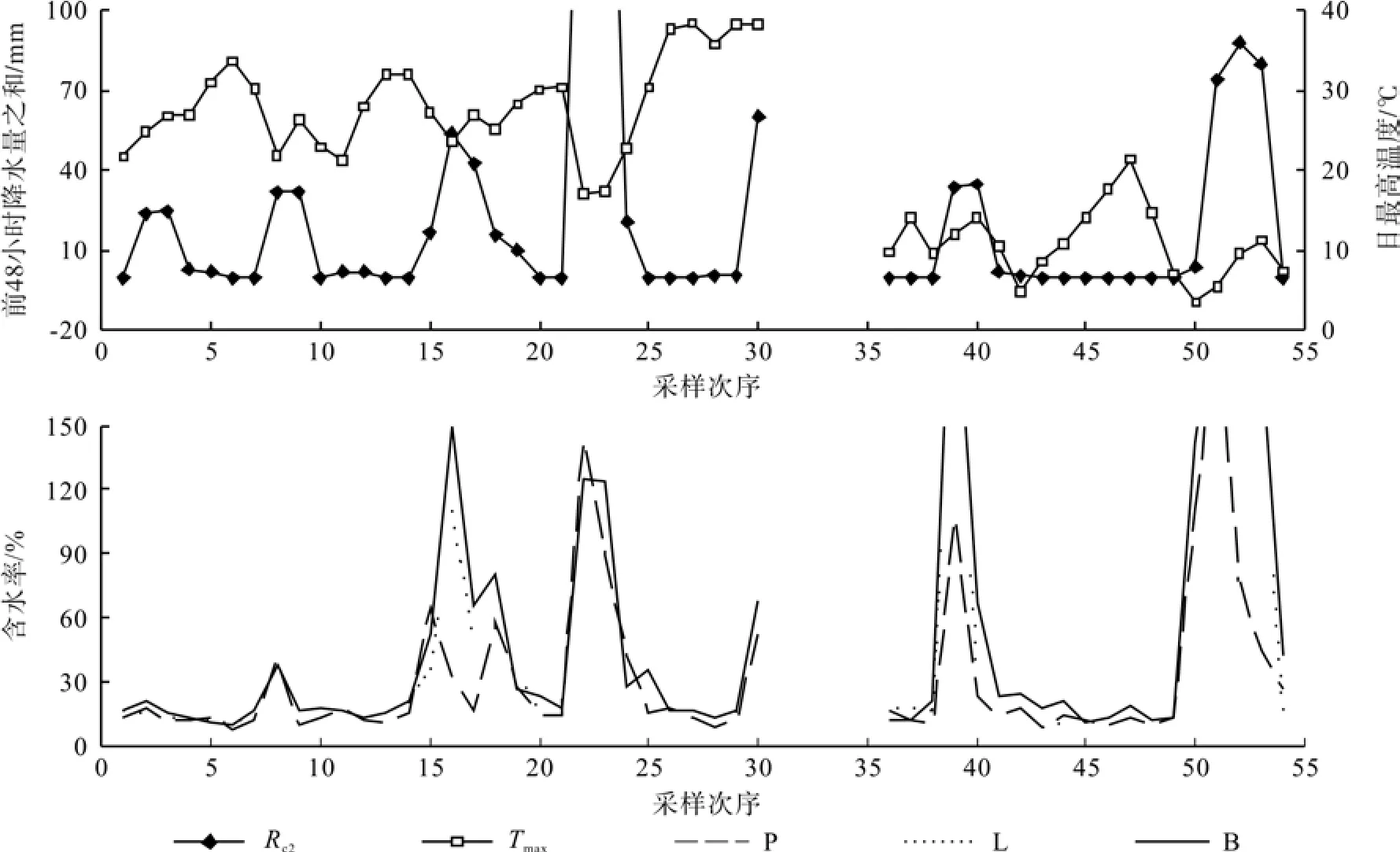
图1 前48小时降水量之和、日最高温度和可燃物含水率的动态变化Fig.1 Dynamics of measured sum of first 48-hour rainfall, daily maximum temperature and fuel moisture contents

表 2 Pearson相关系数†Table 2 Pearson correlation coefficients

表2给出地表死可燃物含水率与气象因子的Pearson相关系数。可以看出降水量和前n天平均相对湿度的Pearson相关系数较大，说明这些因子对含水率的变化影响显著。

2.2 不同季节、有无降雨的可燃物含水率预测模型

使用逐步回归的方法筛选出对可燃物含水率预测模型有影响的气象因子。包括：前2天平均相对湿度、前4天平均相对湿度、2天前当日平均湿度、4天前当日平均风速、前1天降水量之和、前3天降水量之和、前24 m（m=1～3）小时降水量之和等。所构建的模型可以解释含水率变差的45.5%～99.7%，3种林型中，在无降雨期模型调整后决定系数全部高于0.902，说明拟合模型精度高。

2.3 季节对模型误差的影响

由表3和图2知，樟子松林模型MAE在无降雨期春季最小，秋季误差最大；降雨期春季最小，春-秋季最大；混合期春季和秋季相差不多，春-秋季最大。落叶松林模型MAE在无降雨期春季和秋季接近，春-秋季误差最大；降雨期春季、春-秋季、秋季依次增大；降雨混合期春季最小，春-秋季最大。白桦林模型误差在无降雨期春季和秋季接近，春-秋季最大；降雨期春季最小，秋季和春-秋季都很大；降雨混合期春季最小，春-秋季最大。樟子松林模型MRE在无降雨期春季和春-秋季最小，秋季误差最大；降雨期春季和春-秋季小，秋季最大；混合期春季和秋季最小，春-秋季最大。落叶松林模型MRE在无降雨期春季和秋季接近，春-秋季误差最大；降雨期春季最小，秋季和春-秋季最大；降雨混合期春季和秋季接近，春-秋季最大。白桦林模型MRE在无降雨期春季和秋季接近，春-秋季最大；降雨期春季最小，秋季和春-秋季都很大；降雨混合期春季和秋季相差不大，春-秋季最大。这表明，对于不同林型而言，气象要素回归法的春季效果最好，秋季效果较差，春-秋混合效果不太好。

限于篇幅，图3只给出了3种林型在不同季节无降雨期的含水率实测值与预测值的对比，降雨期和混合期模型的实测与预测值对比没有给出。从图3可以看出，可燃物含水率预测和实测散点集中在1∶1直线周围，说明地表细小可燃物含水率模型预测偏差小。3种林型含水率预测精度由高到底依次为樟子松林、白桦林和落叶松林。

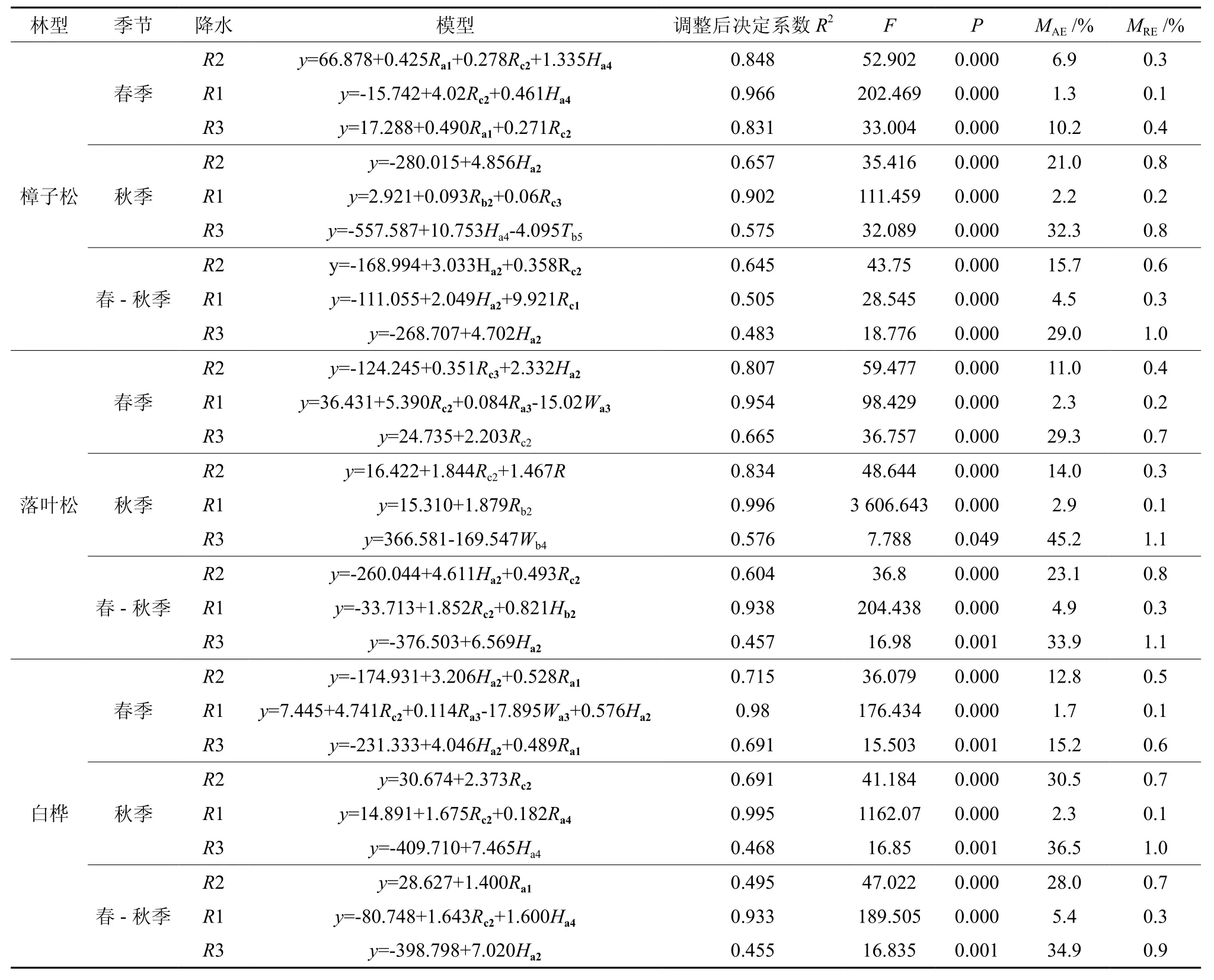
表 3 可燃物含水率模型的参数和检验†Table 3 Parameters and testing of moisture prediction models

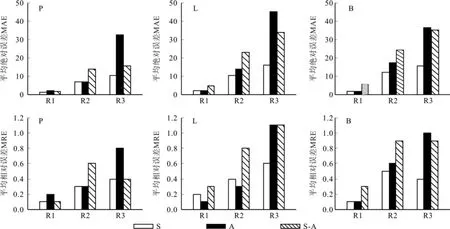
图2 不同季节时模型的误差对比Fig.2 Comparison of model errors in different seasons

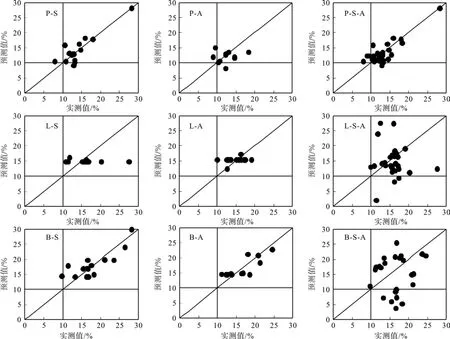
图3 不同季节实测值与预测值的对比（以无降雨期为例）Fig.3 Comparison between measured and predicted values in different seasons (in case of no rainfall)

2.4 降雨对模型误差的影响分析

由表3和图4知，樟子松林模型MAE在春季无降雨最小，混合降雨期次之，有降雨最大；在秋季无降雨最小，有降雨最大，在春-秋季无降雨最小，混合降雨和有降雨相似，都比较大。落叶松林模型MAE在春季无降雨最小，混和降雨期次之，有降雨最大；在秋季无降雨最小，有降雨最大，在春-秋季无降雨最小，有降雨最大。樟子松林模型MRE在春季无降雨最小，有降雨最大，在秋季无降雨和混合降雨接近，有降雨最大，在春-秋季无降雨最小，混合降雨最大。落叶松林模型MRE在春季无降雨最小，有降雨最大，在秋季无降雨和混合降雨都很小，有降雨最大，在春-秋季无降雨最小，混合降雨和有降雨都较大，有降雨最大。白桦林模型MRE春季无降雨最小，混合降雨和有降雨接近，混合降雨最大，在秋季无降雨最小，有降雨最大，在春-秋季无降雨最小，混合降雨和有降雨都很大。这表明，对于不同林型而言，气象要素回归法对无降雨时段效果最好，有降雨时段和混合降雨效果较差。含水率受降雨条件影响大，没有降雨导致死可燃物含水率变化幅度小，所以此时的预测模型准确度大，而在降雨期时，死可燃物含水率变化剧烈，误差增加。如果综合考虑季节和降雨，无论是MAE还是MRE，各林分预测模型均是无降雨模型误差最小，降雨模型误差最大。

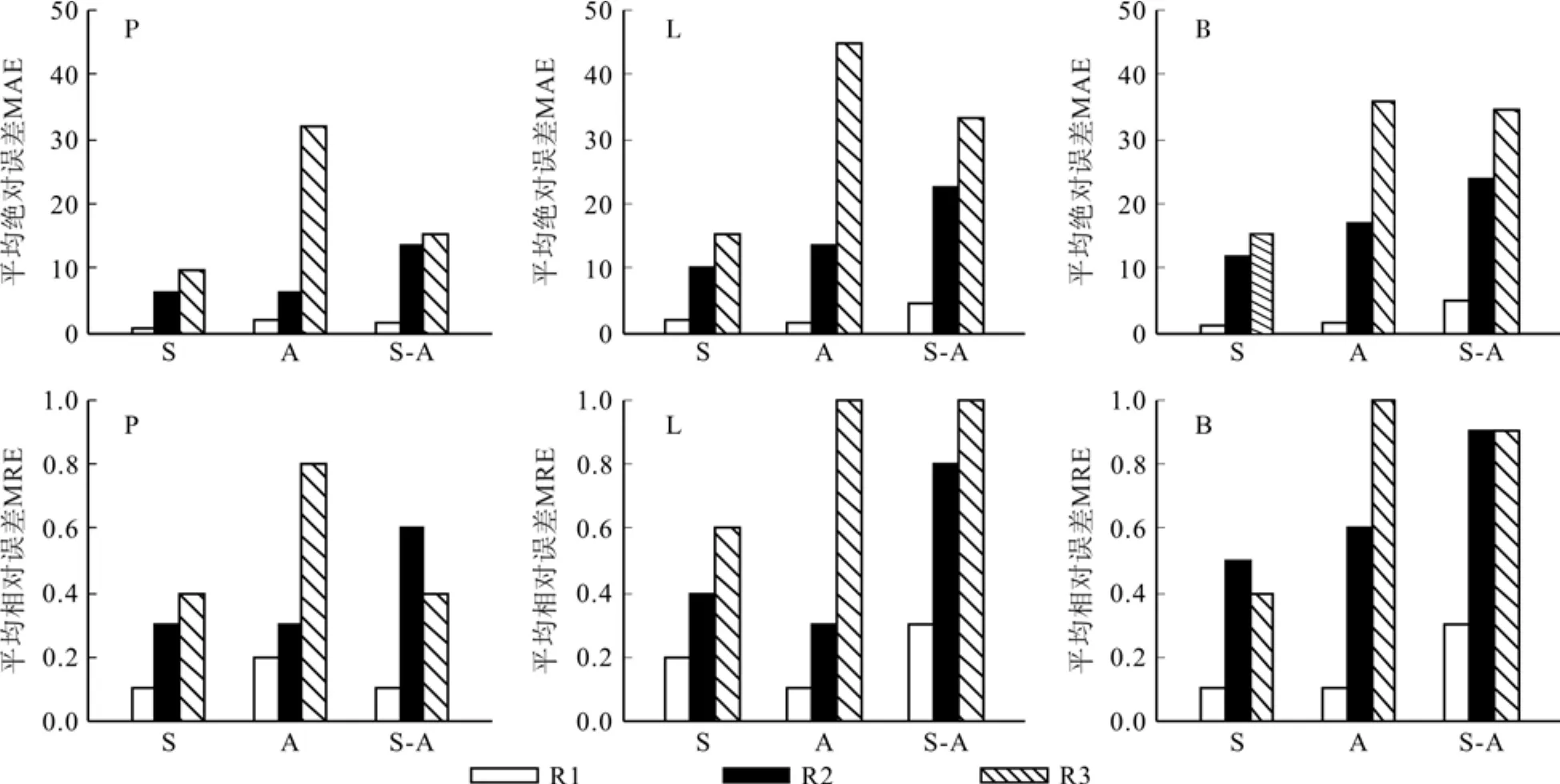
图4 不同降雨期模型的误差项对比Fig.4 Comparison among model errors in different rainfalls

图5给出了3种林型在春-秋季各降雨期的含水率实测值与预测值的对比，春季和秋季模型的实测与预测值对比没有给出。从中可见，各林型在不同降雨的散点分布在1∶1线周围，可以看出结果较好。与分季节模型相似，预测精度由高到低依次为樟子松林、落叶松林和白桦林。

3 讨 论

季节和降雨对气象要素回归法建立的含水率预测模型的精度具有显著的影响，春季模型的精度一般高于秋季或春秋两季混合；无降雨时段的精度要高于有降雨时段或混合时段。春季无降雨时段模型的精度最高，此时是该地区森林火险最高的时段，气象要素回归法对于该时段十分有效。对于其他时段，特别是有降雨的时段，虽然误差较大，但因为有降雨时可燃物含水率比较高，森林不燃[17-18]，火险等级低，即使火险等级预报有误，影响也较小。虽然气象要素回归法的误差较时滞平衡含水率法等大一些，但如果采用区分季节和降雨时段建立模型，对林火预报有较好的参考价值。而且如果不使用气象站的温度数据，而采用地表可燃物温湿度，可以提高模型精度[19]。建立区分季节和降雨时段的气象要素模型将有助于提高火险预报的针对性。而不区分季节和降雨的气象要素回归法将可能在干燥时段高估可燃物含水率，造成预报火险等级低于实际等级，影响森林防火工作。

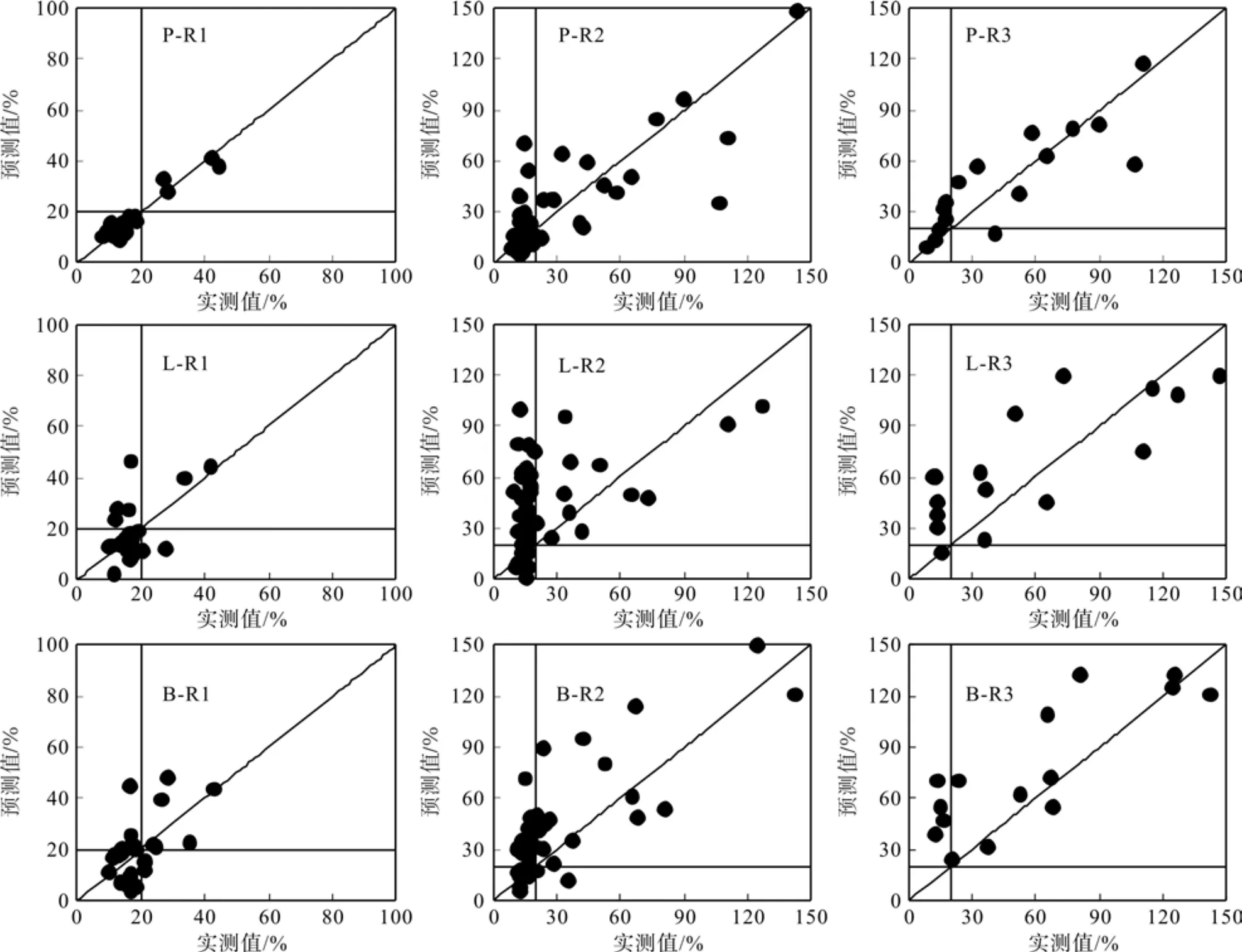
图5 不同降雨实测值与预测值的对比（以春-秋季为例）Fig.5 Comparison between measured and predicted values with different rainfall types (in case of Spring and Autumn)

本研究所建预测模型仅适用于与本研究立地条件相似的地区，这一条件所指的就是包括树种、地形等在内的稳定少变因子[20]。本研究中，樟子松林在各个季节和不同降雨时期的模型误差都要小于落叶松林和白桦林，后两种林型在各时期误差比较接近，这应该与地形关系较大，樟子松林位于阳坡坡上，且郁闭度较低，而落叶松林和白桦林位于阳坡坡中，且郁闭度较高（表1），在较大降雨发生后，在相同的大尺度气象因素下，樟子松林地表死可燃物失水速度较落叶松林和白桦林快，对气象因子响应明显，因此，模型能更好反映实际情况。

本研究中的无降雨期研究结果与居恩德[21]，构建的模型大兴安岭地区樟子松林、落叶松林和白桦林中应用的R2在0.838以上相似，这说明了以不同季节和降雨情况建立分段模型的有效性。实际上，本文所建立的春-秋季混合降雨模型相当于之前大多数研究中没有对季节和降雨进行区分的常规含水率预测模型，三个林型R2在0.604～0.679，MAE在14.0%～24.1%，与之前杜秀文、覃先林等学者所建立的预测模型相比，对观测值的拟合程度不是很好，误差相对较大，而在春季无降雨火险程度最高时期，R2全部大于0.902，MAE为1.3%～2.3%，在本次的研究中效果最好，是因为居恩德等人的气象和林分条件与本研究的气象林分条件类似模。秋季降雨条件时模型精度低可能也与其观察数据少相关，在以后的研究中要增加观测样地，提高模型预测精度。

[1] Anderson H E. Mechanisms of fire spread[P]. Research progress report No.1.United States Department of Agriculture. Forest Service Research Paper INT-8. Ogden. Intermountain Research Station, 1964.

[2] Rothermel R C, Wilson R A, Morris G A,et al.Modeling Moisture Content of Fine Dead Wildland Fuels: Input to the BEHAVE Fire Prediction System[P]. USDA Forest Service Research Paper INT-359. Ogden, UT: Intermountain Research Station, Forest Service,United States Department of Agriculture, 1986.

[3] 王瑞军, 于建军, 郑春艳. 森林可燃物含水率预测及燃烧性等级划分[J]. 森林防火,1997, 2: 16-17.

[4] Nelson RM. Prediction of diurnal change in 10-hour fuel moisture content[J]. Canadian Journal of Forest Research, 2000,30(7): 1071-1087.

[5] 金 森, 李绪尧, 李有祥. 几种细小可燃物失水过程中含水率的变化规律[J]. 东北林业大学学报, 2000,28(1): 35-38

[6] Nelson RM. Prediction of diurnal change in 10-hour fuel moisture content[J]. Canadian Journal of Forest Research, 2000,30(7): 1071-1087.

[7] 刘 曦, 金 森. 基于平衡含水率的森林可燃物含水率预测方法的研究进展[J]. 林业科学, 2007, 43(12): 126-133.

[8] Weidman RH. Relation of weather forecasts to the prediction of dangerous forest fire condition[J]. Monthly Weather Review,1923,11: 563-564.

[9] Gisborne. HT. Using weather forecasts for prediction forest fire danger. Monthly Weather Review.Matthews S, McCaw WL,Neal JE, et al. 2007[J]. Testing a process-based fine fuel moisture model in two forest types. Can J For Res,1925,37: 23-35.

[10] 卢欣艳, 牛树奎, 任云卯. 北京西山林场可燃物含水率与气象要素关系[J]. 林业资源管理, 2010,(3): 79-86.

[11] 张大明, 杨雨春, 张维胜, 等. 可燃物含水率与气象因子相关关系预测模型的研究[J]. 吉林林业科技,2010,39(3): 27-39.

[12] 高永刚, 张广英, 顾 红, 等. 森林可燃物含水率气象预测模型在森林火险预报中的应用[J]. 中国农学通报,2008,24(9):181-185.

[13] 王金叶, 车克钧, 傅辉恩, 等. 可燃物含水率与气象要素相关性研究[J]. 甘肃林业科技，1994,(2): 21-23.

[14] 覃先林, 张子辉, 易浩若, 等. 一种预测森林可燃物含水率的方法[J]. 火灾科学，2001,10(3)：37-40.

[15] 张国防, 林文革, 花昆福, 等. 杉木人工林地表易燃物含水率变化规律[J]. 福建林学院学报, 2000,20(1): 77-79.

[16] 罗永忠, 车克钧, 蒋志荣. 祁连山林区森林可燃物含水率变化规律研究[J]. 甘肃农业大学学报, 2005,2(40): 239-244.

[17] 金 森, 李 亮, 赵玉晶. 用直接估计法预测落叶松枯枝含水率的稳定性和外推误差分析[J].林业科学,2011,47(6):114-121.

[18] 金 森, 颜雪娇. 帽儿山地区10种灌木生长期内含水率动态变化规律及预测模型研究[J]. 应用生态学报, 2012,23(12):96-103.

[19] 金 森, 周 勇. 昆明典型地表死可燃物含水率预测模型的研究[J]. 中南林业科技大学学报, 2014,34(12): 7-15.

[20] Matthews S, McCaw WL, Neal JE,et al. Testing a process-based fine fuel moisture model in two forest types[J]. Can J For Res,2007, 37: 23-35.

[21] 居恩德. 可燃物含水率与气象要素相关性的研究[J]. 森林防火, 1993,1: 17-21.