谈初中数学教学中学生的反思

林日镜

[摘 要] 本文结合“探索勾股定理”的教学实践，从学生学后反思中反思教师的“教”和学生的“学”，探讨如何彰显学生主体地位的问题.

[关键词] 反思；学情；引导

怎样找到一个最接近学生学习真相的观察点，来了解教师的“教”和学生的“学”是否有效呢？除了采取直接观察法之外，追踪、分析学生对自身参与课堂活动的体悟与反思信息显得尤为重要. 本文以“探索勾股定理”一课的教学为例，略加阐述.

教学简要过程

1. 从《九章算术》中的一道题导入，激发探究欲：该怎样解决这一问题？

问题：《九章算术》中的一道题——今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深、葭长各几何？

2. 预设学生遭遇障碍，暂时搁置问题，先提供一组题目，供学生自由选择、探索.

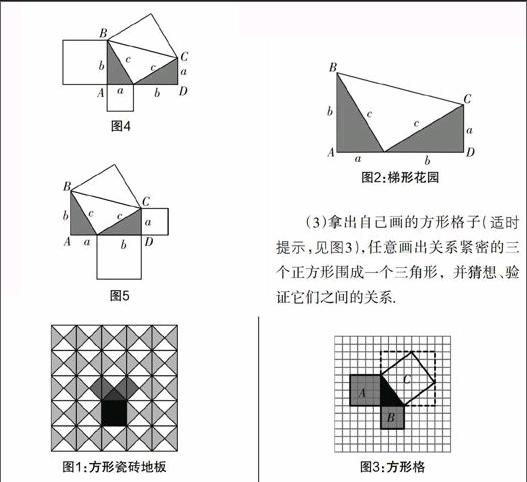
（1）猜测、验证图1黑色的大正方形与浅灰色的两个小正方形面积之和的关系；

（2）猜测、验证图2白色的三角形与浅灰色的两个三角形（均为直角三角形）面积之和之间的关系；

（3）拿出自己画的方形格子（适时提示，见图3），任意画出关系紧密的三个正方形围成一个三角形，并猜想、验证它们之间的关系.

从以上三个活动中，你发现了什么？

得出结论：勾股定理.

学生课堂反思实录

师：心理学家告诉我们，善于归纳、总结和反思能够极大地巩固知识和提高学习能力. 现在，请同学们说说你从这堂课学到了什么？

生1：我懂了什么是勾股定理，不会忘记它. 因为，这是我和大家一起得出的.

生2：这节课，我好像走入了一座迷宫，但在大家的帮助下又走了出来，很享受.

生3：一开始我不知道老师为什么要举出《九章算术》的例子，最后才明白，原来老师是想吸引我们学习勾股定理，告诉我们中国是一个了不起的数学王国.

生4：也告诉我们，数学很有用.

生5：勾股定理好像一位神秘人，早就等待着我们去寻找它.

生6：我发觉，利用勾股定理可以编出好多题目，解决好多问题.

……

反思学生的“学”

数学课上，学生如果始终处在主体地位，观察、实践、思考、分析、提炼、归纳、建模、演习等一系列思维活动就会处在积极的状态.

1. 自我建构：亲身经历，切肤之感. “任何真正的学习都是主动的、不可替代的”，所有的学生都有一个共同的体会，即数学知识理解得透彻，知识记得牢靠，留在记忆中的印象较为深刻，这比被动接受教师单线灌输学习的效果要强烈得多. 生1因为“和大家一起得出”勾股定理，点点滴滴都是在他们亲身探索、亲手创造、亲切互动的过程中体验、累积起来的，是最为宝贵的生成. 对他们来说，勾股定理成为他们自身的真实发现，他们做了一回独属于他们拥有的数学知识的发现者. 所以，他们明白了勾股定理所产生的价值，可以“编出好多题目，解决好多问题”（生6），他们会进一步改变数学枯燥、偏离生活实际的错误观念，真切地认识到“数学很有用”（生4）.

可见，知识、技能只有经历习得的过程，学生才能“刻骨铭心”.

2. 彼此激励：相互给予，相携而进. 学困生、中等生，甚至优等生，在探索过程中，都可能遭遇门槛，产生疑惑. 这是他们最没有安全感、特别迷茫的时候，而同伴之间的相互支持、各取所长，能帮助他们获得心理安慰，从对方身上汲取探索的智慧和力量，从而体会到“山重水复疑无路，柳暗花明又一村”的顿悟感. 生2的反思即是如此. 《九章算术》中的这道题使他们茫然无措，但是他们在经历了探索过程之后，利用探索的结果合作克难，最终解决了，他们的心中就会感受到集体的力量.

反思教师的“教”

教是为了不教，教知识不如教学法. 教就是为了学而存在；学才是教的价值体现. 学的效果如何是评价教的效果的唯一标准. 因此，学生的课后反思再一次告诉我们：

1. 以学定教. 基于学情的教才是最贴近实际、最为学生欢迎的行动. 笔者查阅了关于“勾股定理”的教学设计，综合了它们的优点，制定了本课的教学方案. 这个方案力图彰显学生的课堂主人翁地位，充分考虑学生已有数学知识和技能的积淀，设置问题探索的情境，处处引导学生. 所提供的探索素材各有特点：《九章算术》中的是文字型；图2题为几何图形类型；图1、3题为实践型. 这些素材直观、典型，都可以激发学生的想象力、探索欲，其中文字型素材既是有趣、挑战性的导入，又是学生运用勾股定理的理想实验题. 这样的设计如同设置了一个又一个迷宫，营造了一种“一山放过一山拦”的挑战情境，自然会吸引学生步步跟进，始终牵引着学生的探索兴趣. 正是如此，生3才有这样的感慨，意识到教师的导入意图.

2. 以引为上. “不愤不启，不悱不发. ”当学生伸手够不到桃子的时候，教师应当相机现身，为他们略微搭建一个高度合适的梯子，指点迷津. 《九章算术》中水深多少？芦苇长几何？学生一时无法解决这个难题，如果教师给他们出示解题过程，这就使得本课的教学魅力大为降低，而把问题暂时搁置起来，另辟蹊径，通过三次探索活动，学生就可以寻找到一架梯子. 第（1）题以地板瓷砖为例，较容易引起学生的生活联想，而且很快形成数学思维，利用学过的正方形面积公式、三角形全等判定定理、方程式等知识，顺利地找到了三个三角形之间的关系. 第（2）题则以数学语言呈现，学生思考了一会，并没有找到解题的正确途径，这说明学生的学习遇到了瓶颈. 笔者随机提示他们：运用刚才研究“地板瓷砖”的思路；运用数形转化的思想，借助添加辅助线的数学技能. 这一提示，一下子打开了他们的思路，于是学生探索的积极性一下子又高涨起来，出现了几种转化方法，如图4和图5.

小组展示中，我发现，他们完全能够推导出问题的结论：a2+b2=c2. 这已经接近勾股定理的模型了，于是，笔者顺势引导：是不是所有的直角三角形三边都存在这样的关系？这样就继续引导他们猜想、验证，最终得出勾股定理. 随后，笔者安排学生自主实践内容，即第（3）题，引领他们在亲身体验中体会到勾股定理的原理和妙处. 学生在提示下，用割补法体会图形之间的关系，这种所得必定烙在他们的内心深处，找到解决实际问题的钥匙，所以他们能够领略到勾股定理的实际价值，生成一些编制数学题的方向，感受到数学的魅力，领略到丰富的数学文化. 这样，学生最终顺利地给出了导入题的答案. 这个过程其实就是引领和培育学生模型思想的过程，使学生不仅学会“建构基本的数学模型，更重要的是把已有的数学模型进行推广，演绎出更多的数学模型，达到会一个到会一类、以一当十之功效”.

整节课，教师讲得少，学生活动得多；教师穿针引线，科学引导，学生所得必定是多元、深刻而持久的，即“教学相长”. 由此观之，教与学只有处在同一条道路上，教师才能成为真正的首席学习者，我们通过分析学生的反思即可强化这一认识.endprint