数学是偏爱单干的学科吗——兼与吴彤教授商榷

黄松平

(空军空降兵学院，广西 桂林 541003)

在一篇署名为吴彤、乔宏刚、汪立群的论文《论“科研合作研究”性质及其意义——一个科研合作与其对象相关性研究》[1](以下简称“吴文”)中写道：数学是偏爱单干的学科，数学家对“大科学”后的合作热潮无动于衷，与物理和化学等学科合著比例不断上升的趋势相反，数学学科的合著比例呈下降趋势，最终徘徊在15%的水平。[1]事实果真如此吗？我们通过详细统计《数学学报》和《物理学报》中的合著比例，发现这一观点值得商榷。

一、“吴文”认为数学是偏爱单干的学科

“吴文”主要论述了科研过程的合作性质及意义，重点研究了著名科技杂志中的论文合著率及其所反映的合作状况。在统计了美国《物理学评论》、中国《物理学报》和《中国社会科学》(该刊仅统计了1981年和1991年数据)的合著比例状况后，“吴文”由此得出结论：“合作首先是受研究领域和对象制约的产物，而不是研究者之间友谊的结果；其次取决于科学研究的劳动性质。”[1]同时，作者提出：“合作是科学研究自组织发展的结果，同时合作的出现，又进一步激励了科学研究，因而合作研究与科学发展本身是一个交互作用的‘循环’过程，合作既是科研演化的结果，又是科研演化的动力。”[1]

在研究数学学科的合著比例状况时，“吴文”主要统计了《数学学报》1986～1990年论文合著比例。该文称：“在自然科学领域，物理学、化学、生命科学、天文学、地学以及医学的合作研究呈上升趋势，但在数学领域，我们却看到了截然不同的情况。五年来，数学家科研合著比例不仅没有上升，反而有所下降，其总合著比例徘徊在15%左右。对比物理学与此恰恰相反的比例，即合著率平均为85%的状况，人们也许会问：为什么数学家对科学中这一合作热潮竟会如此冷漠？面对艰难的数学王国，数学家们携手同行难道不比单枪匹马更好吗？”[1]“吴文”认为，这种强烈的“反差”实际上是数学学科与其他学科自身的性质不同所造成的：“在科学哲学中，数学被认为是独立于物理实在性的科学，其研究对象自相一致，无需任何特殊实在性之意义。换句话说，数学的真理不在于研究与其对象的符合性，而在于研究的逻辑自恰性。用一些哲学家的说话，就是它是先验的。”[1]

对于数学学科中作者发现的这种“现象”，作者分析指出：“对于数学，一个科学家解决不了的问题，那么同样领域中的10个数学家的合作也一样解决不了这个问题。而数学中抽象问题的解决也很少需要其他领域中的科学家的合作。数学科学的这种独特学科性质使数学家在研究过程中不大可能形成合作关系，他们的研究成果往往是个体思维的结果，而非合作研究的结晶。”[1]由此作者断定：“科学研究中的合作主要取决于科学对象，其次取决于科学研究的劳动性质……有的学科则偏爱单干，有的学科则离不开协作。”[1]

二、基于《数学学报》中的论文合著比例仍呈上升趋势

我们通过详细统计同一刊物(即《数学学报》)的合著比例发现，它并不象“吴文”声称的那样，“其总合著比例徘徊在15%左右。”[1]实际上，数学学科的合著比例和物理、化学等学科一样，也一直呈上升趋势。由此可见，在合著比例这一点上，数学学科一点也不比其他学科例外。

在1954年，《数学学报》中的合著比例为0%，即所有的论文都是由单个人完成的。到了1957年，其合著比例上升到4.9%。随后，1959年、1964年、1977年比例分别为11.6%、11.3%、17.9%(考虑到“文革”的特殊原因，1966～1976年的比例未做统计)。从这里可以看出，在1978年以前，《数学学报》中的合著比例很低，没有超过20%，甚至出现过0%的现象。但从1980～1989年十年间的统计来看，平均合著比例超过了20%，具体为20.2%，其中1983年的合著比例高达29.6%。1990～1999年十年间的平均比例又有所上升，达到28.5%，接近30%的水平(见表1)。

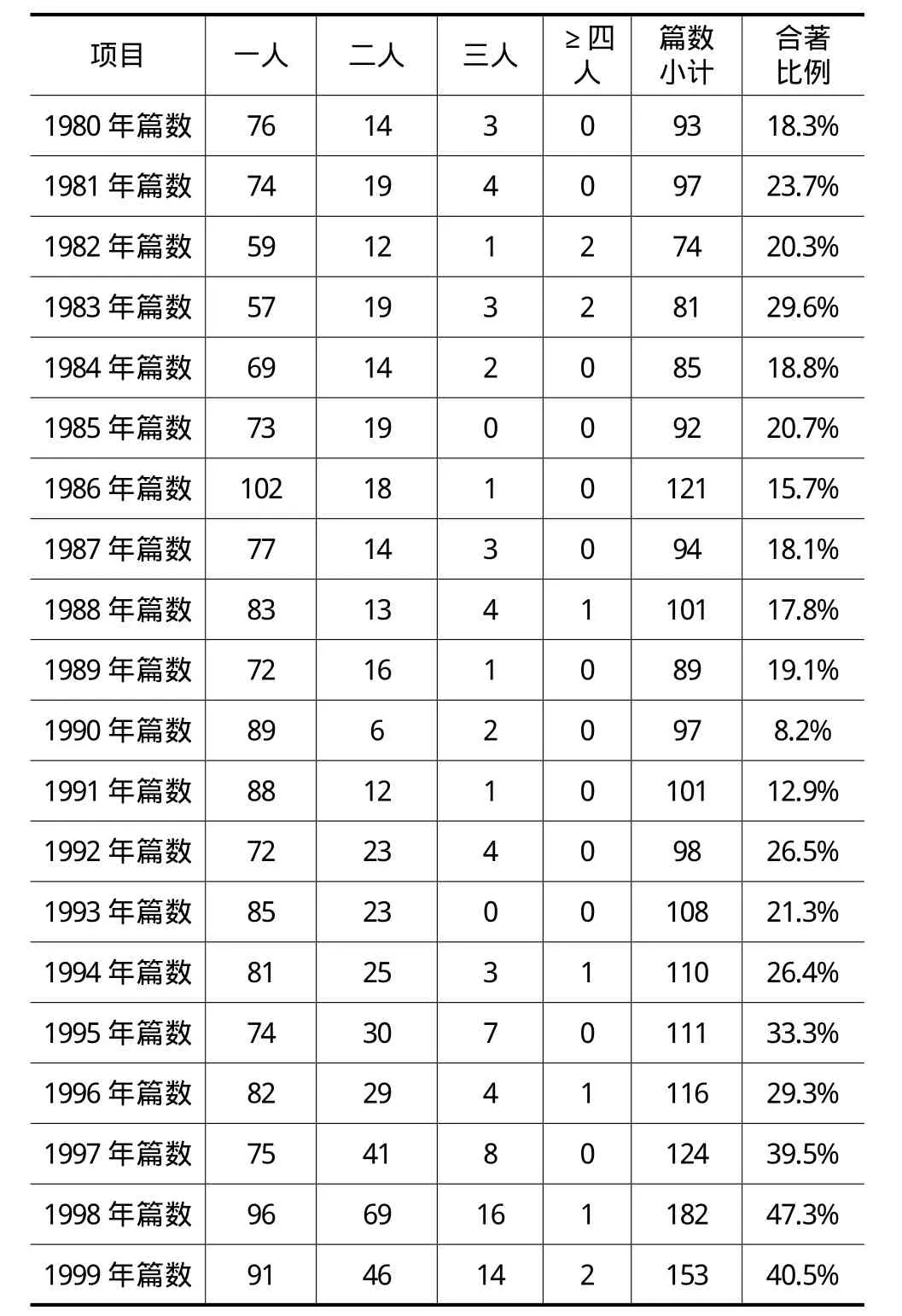
表1 1980～1999年《数学学报》中的合著比例统计

进入21世纪后，这个比例呈增长之势，2000～2003年四年间的平均比例已经到了57.1%，统计中的最近一年，即2003年的合著比例更是高达69.1%，其中25篇是3人及3人以上合作的结晶。以下是2000～2003年《数学学报》中合作的比例统计：

表2 2000～2003年《数学学报》中的合著比例统计

造成“吴文”关于数学合著比例下降的结论原因在于：其统计样本很少，仅统计了1986～1990年的情况。据笔者统计，1986～1990年的平均合著比例为15.8%，确实属于“徘徊在15%左右”。但是，为“吴文”统计在内的1990年的合著比例仅为8.2%，可以算为一个奇异样本，不但远远低于80年代平均比例(即20.2%)，也低于其后几年的比例(如1991、1992、1993年分别为12.9%、26.5%、21.3%)。这个奇异样本为“吴文”得出“徘徊在15%左右”的结论可谓助莫大焉。1986～1990年的合著比例分别为15.7%、18.1%、17.8%、19.1%和8.2%。说它徘徊在15%的水平还算差强人意，但无论如何也不至于说它是反降不升的。因为就单从这5个样本来看，1987年比1986年比例就有所上升，同样的情况也存在于1989年对比于1988年。应该说，这5年的比例呈波浪形，上升与下降是交替进行的。前4年的比例是稳态的，略有上升势头。或许出于与论文前面总结出的“物理学合著比例为85%的状况”形成鲜明对比，因此作出了“数学总合著比例徘徊在15%”的论断。

以年代为样本来计算中国《物理学报》的合著比率，可以看到：20世纪50年代的平均合著比例为38%，“文革”前整个60年代(即1960～1965年)平均合著比例为51.7%，比“吴文”给出的1961年的比例高，而且较为详实和有说服力。1974～1979年(1970～1973年刊物停办)平均合著比例为59.4%。进入20世纪80年代后，合著比例都高于1980年的比例，即都在66.1%以上，说明在20世纪80年代，三分之二以上的论文是合作的结果，其中在1985年，这一比例甚至达到了83.9%，接近1991年的比例(见表3)。

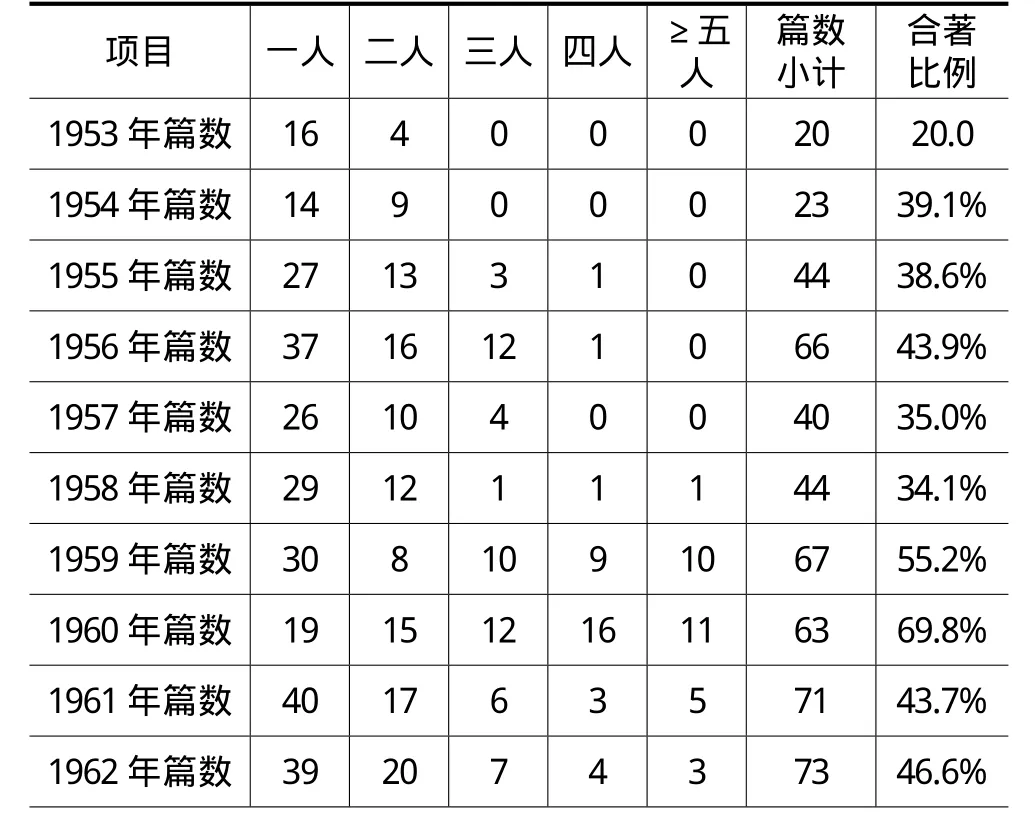
表3 《物理学报》中详细的合著比例统计

1963年篇数 47 17 17 4 3 88 46.6%1964年篇数 79 40 27 3 1 150 47.3%1965年篇数 98 56 38 9 6 207 52.7%1974年篇数 15 6 8 4 5 38 60.5%1975年篇数 27 11 16z 2 10 66 59.1%1976年篇数 30 14 6 13 21 84 64.3%1977年篇数 25 21 10 2 11 69 63.8%1978年篇数 37 20 17 8 7 89 58.4%1979年篇数 53 15 16 8 14 106 50.0%1980年篇数 63 60 25 20 18 186 66.1%1981年篇数 72 66 43 27 18 226 68.1%1991年篇数 45 62 71 51 61 290 84.5%

可见，在物理领域中，合著比例确实呈上升趋势。为什么要统计年代平均比例呢？因为统计样本增多，数据详实，作出的结论无疑更具科学性和说服性。如果样本数目较少，则很难有说服力。甚至会让人怀疑研究者为了验证固有的结论而挑选对自己有利样本，这在科技史上不凡其人。如密立根就被质疑在著名的油滴实验中去除了对自己结论不利的数据。“吴文”关于《物理学报》合作研究比例状况，只给出了5年的样本分析，分别是1956年、1961年、1974年、1981年和1991年的情况。它们对应的总合著比例依次为39%、44%、61%、68%和84%。给人感觉合著比例是逐年攀升的，似乎没有出现波动。然而事实并不是这样的。以1960年为例，当年的《物理学报》总合著比例达到了70%，可以说大大高于1971年61%的比例。但“吴文”并没有把这个年代统计在内。为什么“吴文”在20世纪60年代中就挑选了1961年的总合著比例，而没有挑选其它年份呢？如果作者挑选了1960年的数据，又会是怎么样呢？问题或许就出在这里。如果挑选了1960年的资料来统计，则以上数据变为：39%、70%、61%、68%和84%。这样，合著比例显然有起有伏，并非一直上升了。同样，如果20世纪50年代不是如“吴文”那样选择1956的数据，而是挑选1959年的数据，即55%，则这一组合著比例又变为：55%、44%、61%、68%和84%，这同样也很难说是逐年上升的。

综上所述，“吴文”试图以物理学和数学为例来阐明“科学研究中的合作主要取决于科学对象”是值得商榷的，因此得出“数学家对科学中这一合作热潮竟会如此冷漠”的观点也是与客观情况不相符的。因为这两门学科在论文合著比例上并非走着相反的趋势，数学学科论文中的合著比例也是朝着上升的趋势发展，甚至其增长率还要大些。这固然是由于数学的合著比例起点较低，物理学的合著比例经过长足的发展已经达到一定高度的缘故。实际上，在当代包括数学在内的几乎所有学科的科研合著比例都在呈上升趋势。

三、“大科学”时代科研合著比例上升的原因解析

物理学、数学、化学、生命科学、天文学、地学以及医学等学科论文合著比例不断上升不是偶然现象，是有深刻科技背景的。其主要原因是科学技术发展进入“大科学”时代，出现科研生产一体化趋势，由此导致国家、军队、大学和科研单位如重点实验室人才建设一体化。因此，其论文往往是不同结构的人才群体协作的结晶。

美国物理学家A·芬贝格于1961年首先指出，20世纪二三十年代开始，特别是第二次世界大战爆发以后，科学技术发展进入了“大科学时代”。科学学研究表明，“大科学”有明显的特征：一是科研的难度和复杂性迅速增大，所需要的设备仪器复杂昂贵，参加研究的科技人员及所投入的资金数量都非常庞大；二是科学技术的发展越来越专业化，学科门类越来越多，同时科学劳动的社会分工越来越细化，这使得每个科研人员所能涉及的专业面及工作范围越来越窄，往往需要相互协作攻关；三是科学技术的发展在高度专业化的同时又高度综合化，并且以高度综合化为主要趋势，除出现了许多综合性的交叉学科和边缘学科之外，许多重大的科技问题需要来自不同学科和应用部门的专家学者共同参加。[2]P476因此，在一些大型实验室和科研单位，往往形成了既有科学家，又有技术人员和高技能人才的群体结构，当然还包括技术管理专家，这在物理实验室表现得尤为突出。这一点并不显得奇怪。“‘大科学’的出现最先是在高能实验物理和天文学研究。这是因为有些项目需要大量的资源和众多的科研人员共同参与，以及在良好的协调管理之下才能完成。”[3]这也很好地解释了一个现象：即我们在统计《物理学报》合著比例时，发现很多论文署名是××研究小组或实验室，这无疑在一定程度上提高了论文的合著比例。

科学、技术、生产之间以及各门科学和各项技术之间的关系空前紧密，这种密切是通过有组织的社会活动实现的。20世纪40年代以后，人们通过大量的与公司、企业结合的科研、技术、生产一体化的“科学——工业综合体”，或“科学技术研究中心”一类组织，使科学、技术和生产之间的联系以及从技术到工业应用之间的连接变得空前密切了。[4]P14科学通过技术变成直接的生产力。数学作为一门基础学科，在解决工程技术问题上起到了不可替代的作用。如数学家冯康在修建刘家峡水利枢纽工程中独创有限元法，为推进工程进度起到至关重要的作用。在统计中，我们发现数学合著比例不断上升的原因之一就是不同智力结构的人共同研究课题，然后共同署名发表论文。这种不同结构的人结合在一起，科研成果也较多，往往能接二连三地发表合著论文，真正起到“三个臭皮匠，赛过诸葛亮”的效果。显然，这不是数学家之间的友谊促成的，而是数学学科发展的内在要求。因此，我们再也不能简单地认为数学是独立于物理实在性的科学，也不能断定数学就是一门偏爱单干的学科，更不能将数学家视为一群对合作热潮无动于衷的异类。

美国著名女社会学家哈里特·朱克曼在其1977年所著的《科学界的精英》一书中的统计就很能说明问题。她研究发现，从1901年到1972年，在获诺贝尔奖金的286人中，因协作研究获奖的人数有增加的趋势，在杂志上发表的多人合作的论文数也是不断增加的。按照她的统计，1901～1925年因协作获诺贝尔奖的比例为40%，1951～1972年这个比例达到了79%；同一阶段在杂志上发表的多人合作论文的比例分别为25%和71%。这表明，合作研究正在变成科学研究工作的主要方式，合作进行研究的科学家乃是科学研究的“主导力量”。我国的情况也大致如此。我国1983年上半年国家科委评审的59项发明中，有49项是两人以上完成的，占总数的83%。目前，越来越多的科技工作者认识到：合作进行研究是科学工作中的主要方法和形式。[5]P129

值得指出的是，我们说“大科学”条件下的科研活动具有群体性的发展趋势和特点，并不意味着否定个体创造者的作用和作为。某些科技哲学专家评论的“单枪匹马的研究时代一去不复返”的真正含义，也不是断定科学家孤军奋战已无存在的价值，而是强调科研活动的社会性越来越明显的特点。科学家单干的情况在将来不仅存在，而且在促进科学进步中依然发挥着不可或缺的作用。鲁迅先生在百年以前，针对中国重群体轻个人的传统文化，发出了“任个人而排众数”[6]P46的呐喊，虽是鲁迅年轻气盛时为矫枉过正而发，却与马克思、恩格斯“每个人的自由发展是一切人的自由发展的条件”的经典理论相一致，值得百年之后关心科技创新的人们深思。

四、结语

我们通过重新确定样本区间发现，在中国《物理学报》的统计中，20世纪50年代的平均合著比例为38%，“文革”前的整个60年代(即1960～1965年)，平均合著比例为51.7%，70年代为59.4%，80年代这一比例为75%。由此得到的一组比例为：38.0%、51.7%、59.4%和75.0%，总合著比例整体上呈上升趋势。这样以整个年代的平均数为研究对象，避免了挑选样本的主观性。同样，以年代为单位统计，《数学学报》中的合著比例也呈上升势头：由80年代前的从未超过20%到80年代略强于20%，到90年代接近30%，再到近几年合著比例高达57%。可以说，数学并不是偏爱单干的学科，数学家也并不对科学中这一合作热潮显示出冷漠。其它学科，如生物、化学、天文学等的情况与其大同小异。以化学为例，“据美国《化学文摘》统计，1901年全部化学论文的80%以上只有一个作者，20%以下有两个作者，而其中大多数是科学家与助手或学生共同发表，到1963年一个作者的论文只占总数的32%，两人合作的占43%，三人合作的占15.5%，四人以上的占9.5%。近年来论文作者的合作人数更有增加的趋势。”[7]P29由此可见，在“大科学”背景下，几乎所有学科都将从单干转向联合研究、群体攻关，即便像数学这样传统认为是“偏爱单干”的学科也不例外。“大科学”时代，人才群体互补的功能将越来越得到充分地发挥，其作用也越来越明显，合作的比例和范围也越来越大，这是“大科学”发展的必然，[8]也是科技发展折射在人才结构上的一种新的体现。

[1]吴彤，乔宏刚，汪立群.论“科研合作研究”性质及其意义——一个科研合作与其对象相关性研究[J].大自然探索，1996，(4).

[2]温熙森，匡兴华.国防科学技术论[M].长沙：国防科技大学出版社，1995.

[3]蒲慕明.大科学与小科学[J].世界科学，2005，(1).

[4]高惠珠.科技革命与社会变迁[M].北京：学林出版社，1999.

[5]马桂秋.科技人才学[M].杭州：浙江教育出版社，1987.

[6]鲁迅全集(第1卷)[M].北京：人民文学出版社，1991.

[7]邸鸿勋等.科技人才的培养与管理[M].北京：教育科学出版社，1984.

[8]吕莹.我国职务作品著作权及其归属制度完善研究——以《著作权法》第三次修改为视角[J].邵阳学院学报(社会科学版)，2014，(4).