矩阵方程AX＝B的W准反对称最小秩解*

杜玉霞，梁武，费时龙

(宿州学院数学与统计学院，安徽宿州 234000）

矩阵方程AX＝B的W准反对称最小秩解*

杜玉霞，梁武，费时龙

(宿州学院数学与统计学院，安徽宿州 234000）

给定X，B∈Rn×m和正整数s，在集合W－1ASRn×n中寻找矩阵方程AX＝B的解A，使得r(A)＝s；当解集，在S1中确定最大、最小秩解.

W准反对称矩阵；矩阵方程；最大秩；最小秩

设Rn×m表示所有n×m实矩阵的集合；ASRn×n和ORn×n分别表示所有n×n反对称和正交矩阵的集合；记号AT，A+，A－和r(A)分别代表矩阵A的转置、Moore－Penrose广义逆、内逆、和秩；记号LA和RA表示由A决定的两个投影LA＝I－AA－和RA＝I－A－A；矩阵I和0分别表示单位阵和零矩阵.

近年来，由于矩阵秩方法的应用，不少作者对线性矩阵方程的最大、最小秩问题做了研究.例如，王［1－5］得到了一些有关四元素矩阵方程系统的重要结论；田［6］得到了矩阵方程A＝BX+YC的最小秩解；肖［7］研究了矩阵方程AX＝B的对称最小秩解.此处研究矩阵方程AX＝B的W准反对称解，从解集中找出它的最大、最小秩解，并得到指定秩的W准反对称解.当W＝D2时，所研究的问题就变为D反对称矩阵的最小秩问题［8］，并且当W＝In时，所研究的问题就变为反对称矩阵的最小秩问题，即矩阵方程AX＝B的反对称最小秩解、D反对称最小秩解都是文中特例.

1 引理

引理1［9］设矩阵A，B，C，D分别为m×n，m×k，l×n，l×k矩阵，那么

其中G＝CRA，H＝LAB.

引理2［10］给定矩阵X，B∈Rn×m，设WX的奇异值分解为

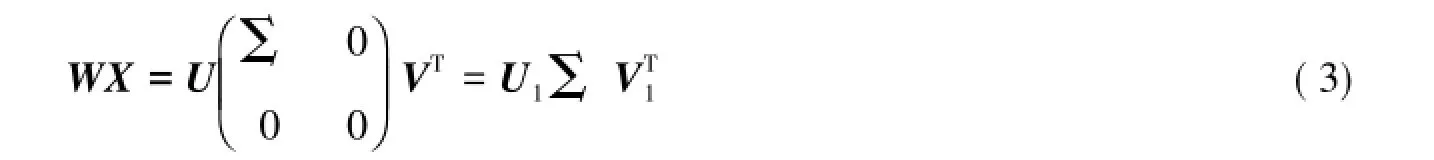
2 结论及证明

定理1给定矩阵X，B∈Rn×m和一个正整数s，设WX的奇异值分解为式(3)，那么矩阵方程AX＝B具有秩为s的W准反对称解的充要条件为

证明假设式(4)成立，由引理2，矩阵方程AX＝B的W准反对称解的一般形式为

由式(5)，(7)－(10)和引理1，得到矩阵方程AX＝B的W准反对称解的最大秩为

与最小秩解的讨论类似，矩阵方程AX＝B的W准反对称最大秩解为

综合式式(4)，(11)－(16)，得到了定理1的结论.

［1］WANG Q W.Extreme Ranks of a Quaternion Matrix Expression Subject to Consistent Systems of Quaternion Matrix Equations with Applications［J］.Appl Math Comput，2006(182)：1755－1764

［2］WANG Q W.Extreme Ranks of the Solution to a Consistent System of Linear Quaternion Matrix Equations with an Application［J］.Appl Math Comput，2007(189)：1517－1532

［3］WANG Q W.Extreme Ranks of a Linear Quaternion Matrix Expression Subject to Triple Quaternion Matrix Equations with Applications［J］.Appl Math Comput，2008(195)：733－744

［4］WANG Q W.Ranks and the Least－norm of the General Solution to a System of Quaternion Matrix Equations with an Applications［J］.Linear Algebra Appl，2009(430)：1626－1640

［5］WANG Q W.The Real Solutions to a System of Quaternion Matrix Equations with Appications［J］.Communication in Algebra，2009(37)：2060－2079

［6］TIAN Y.The Minimal Rank of the Matrix Expression A－BX－YC［J］.Missouri J Math Sci，2002(14)：40－48

［7］XIAO Q.The Symmetric Minimal Rank Solution of the Matrix Equation AX＝B and the Optimal Approximation［J］.Electronic Journal of Linear Algebra，2009(18)：264－273

［8］ZHANG Z.Least－square Solutions to Inverse Problems for D－anti－symmetric Matrices［J］.Journal of Central South University of Technology：Nat Sci Ed，2001(32)：545－548

［9］TIAN Y.The Maximal and Minimal Ranks of Some Expressions of Generalized Inverse of Matrices［J］.Southeast Asian Bull Math，2002(25)：745－755

［10］TANG Y.Least－squares Solution of Inverse Problems for W－para－anti－symmetric Matrices［J］.J Wuhan Univ：Nat Sci Ed，2009(55)：651－655

The W－para－anti－symmetric Minimal Rank Solution of the Matrix Equation AX＝B

DU Yu-xia，LIANG Wu，FEI Shi-long

(College of mathematics＆statistics，Suzhou Universtiy，Suzhou，234000China)

Given X，B∈Rn×m，and a positive integer s，search A∈W－1ASRn×nfor A of AX＝B，to make r(A)＝s.When the solution set，and determine the W－para－anti－symmetric minimal and maximal rank solutions in S1.

W－para－anti－symmetric matrix；matrix equation；maximal rank；minimal rank

O151

A

1672－058X(2015)04－0028－04

10.16055/j.issn.1672－058X.2015.0004.008

2014－07－11；

2014－09－20.

安徽省高等学校省级自然科学研究项目(KJ2013B288)；宿州学院教学研究项目(szxyjyxm201237).

杜玉霞(1981－)，女，山东定陶人，助教，硕士研究生，从事矩阵方程反问题的研究.