解凸优化问题的一类修正线性近似交替方向法

李慧

(重庆师范大学数学学院，重庆 401331）

解凸优化问题的一类修正线性近似交替方向法

李慧

(重庆师范大学数学学院，重庆 401331）

在解凸优化问题过程中，对已有文献的线性约束条件推广到非线性约束条件，运用了近似交替分解算法；新提出一类修正线性近似交替方向法，并进行了理论分析和和算例比较.

近似交替方向法；非线性约束凸规划问题；可分化方法；线性化；增广拉格朗日

1 预备知识

介绍以下原始凸规划问题

其中θ1：Rn→(－∞，+∞］，θ2：Rs→(－∞，+∞］是闭真凸函数，A是m×n矩阵，B是m×s矩阵；X⊆Rn，Z⊆Rs是闭凸集；c是m维给定向量.问题(P)的拉格朗日函数L：Rn×Rs×Rm→(－∞，+∞］

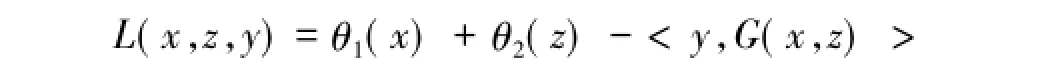
其中＜·，·＞表示内积，·表示欧几里得范数，G(x，z)＝Ax+Bz－c，y是约束Ax+Bz＝c的相应拉格朗日乘子.问题(P)的增广拉格朗日函数为

PADM算法

第2步：若Mk+1－Mk＜ε，则停止，Mk+1就是近似解；否则令k＝k+1，并返回到第1步.

推广模型如下：

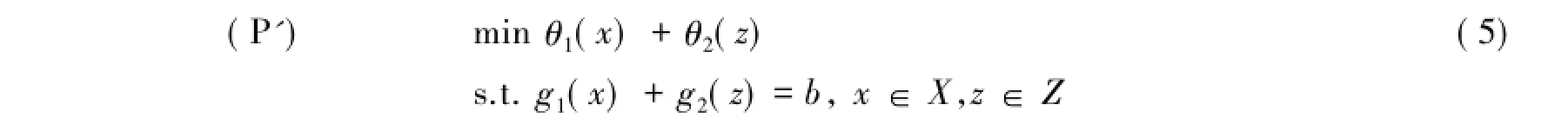
其中θ1：Rn→(－∞，+∞］，θ2：Rs→(－∞，+∞］是闭真凸函数，g1：Rn→R，g2：RS→R是一阶连续可微凸函数，X⊆Rn，Z⊆Rs是闭凸集，b是给定的常数.

对于这种数学规划问题，提出了一类新的可分算法.在算法中，把PADM算法中的二次项依次进行线性化，然后将上一次迭代获得的起始点(xk，zk，yk)和最优点(uk+1，vk+1，wk+1)的凸组合作为下一次迭代的起始点(xk+1，zk+1，yk+1)，称此方法为修正线性近似交替方向法(Modified Linear Proximal Alternating Direction Method)，记为MLPADM.在第2部分介绍一类修正线性近似交替方向法；第三部分应用一类修正线性近似交替方向法进行数值实验；最后通过数据比较得出结论.

2 方法介绍

结合以上提出的PADM方法，对带有非线性约束的凸规划问题，提出了以下3种修正线性近似交替方向法.

第1步：计算

第3步：若Mk+1－Mk＜ε，则停止，Mk+1就是近似解；否则令k＝k+1，并返回到第1步.

3 数值试验

对于各个算例，分别通过PADM和此处提出的MLPADM算法1，算法2，算法3进行比较求解，数值结果记录在表1中.其中M0＝(x0，z0，y0)为任意选取的初始点，M*＝(x*，z*，y*)代表原始问题的近似最优点，θ(x*，z*)＝θ1(x*)+θ2(z*)为近似最优值，Iter代表迭代次数，t/s代表cpu运算时间.

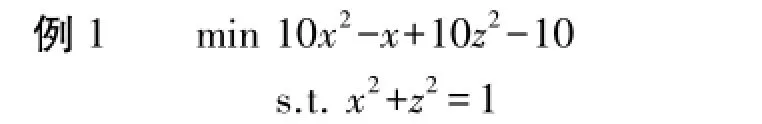
由文献可知最优点为(1，0)，最优值为－1.

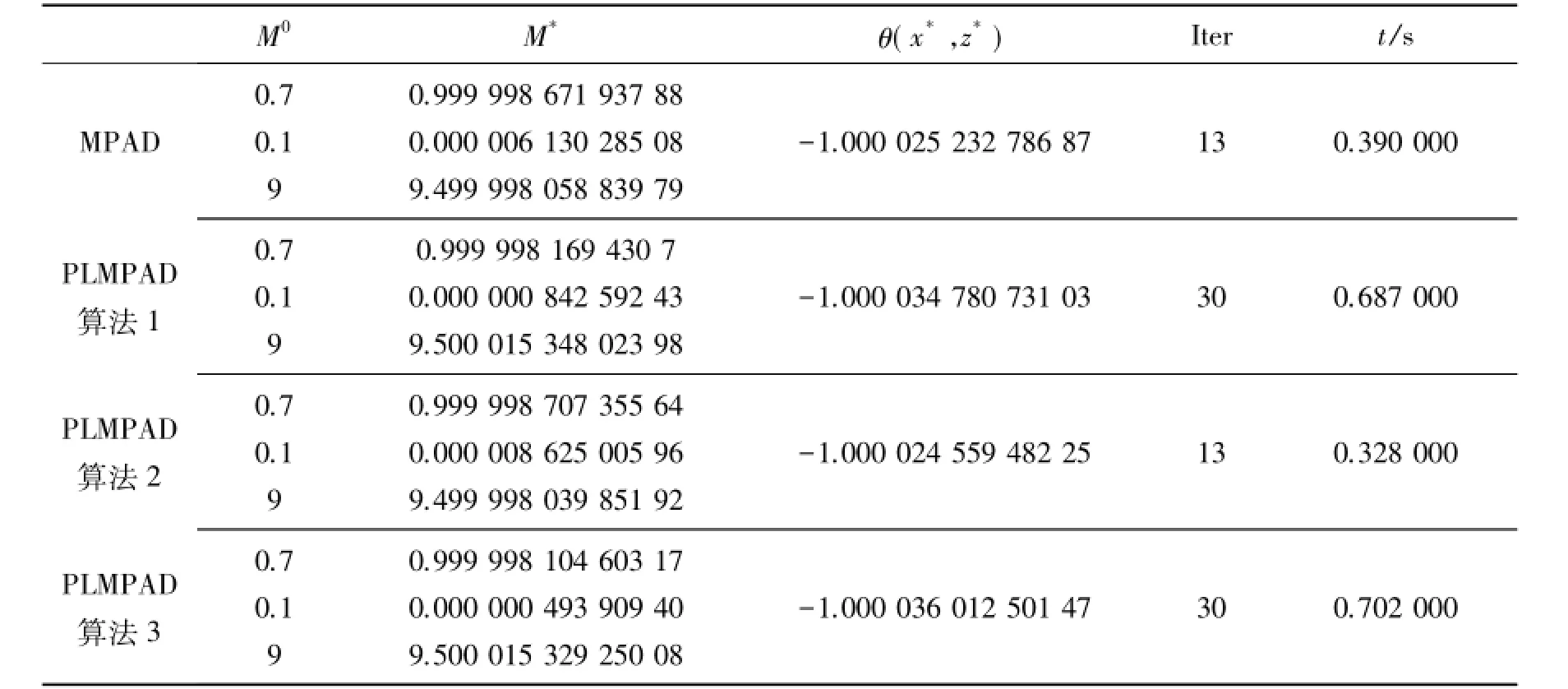
表1 例1的4种算法比较

通过表1可以看出，从迭代次数、运算时间以及最优值比较，显然PMPAD算法2效果好一点.

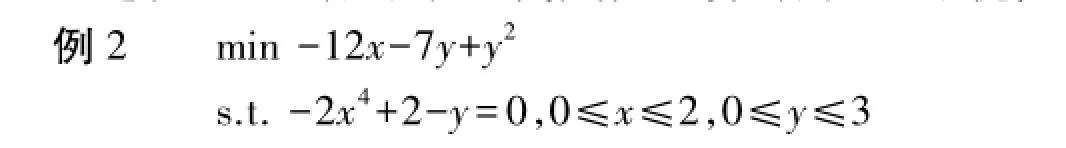
例2最优点为(0.71751，1.470)，最优值为－16.73889.

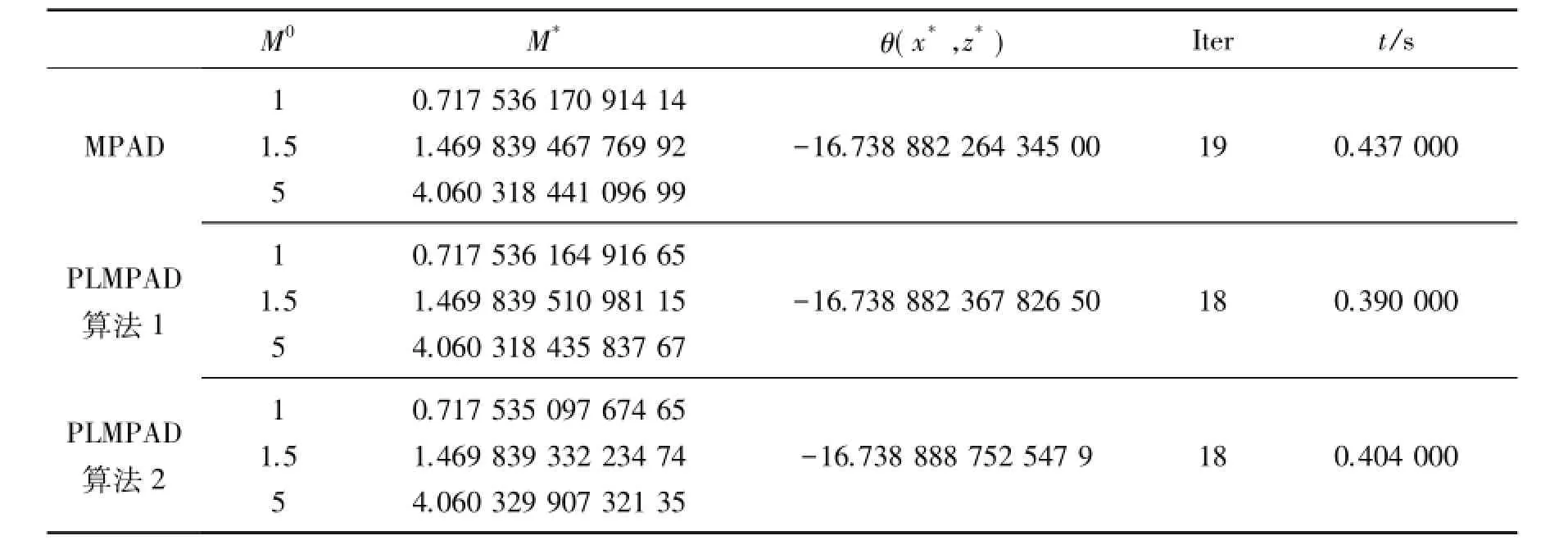
表2 例2的4种算法比较

续表

通过表2观察分析，显然这4种算法中PMPAD算法2效果好一点.

4 结论

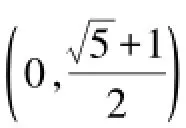
［1］PEACEMAN D W，RACJFORD H H.The Numerical Solution of Parabolic and Elliptic Differential Equations［J］.J Soc Ind Appl Math，1955(3)：28－41

［2］DOUGLAS J，RACHFORD H H.On the Numerlcal Solution of the Heat Conduction Problem in 2and 3Space Variables Trans［J］.Am Math Soc，1956(82)：421－439

［3］DOUGLAS J.GUNN J E.A General Formulation of Alternating Direction Methods，Part I Parabolic and Hyperbolic Problems［J］.Numer Math，1964(6)：428－453

［4］GABAY D，MERCIAR B.A Dual Algorithm for the Solution of Nonlinear Variation Problems via Finite－element Approximations［J］.Computers and Mathematics with Application，1976(2)：17－40

［5］GLOWINSKI R，LETALLEC P.Augmented Lagrangian and Operator Splitting Methods in Nonlinear Mechanics［M］.SIAM Studies in Applied Mathematics，SIAM，Philadelphia，PA，1989

［6］TSENG P.Application of a Splitting Algorithm to Decomposition in Convex Programming and Cariational Inequalities［J］.SIAM J Control and Opti，1991，29(1)：119－138

［7］ECKSTEIN J，BERTSEKAS D P.On the Douglas－Rachford Splitting Menthod and Proximal Point Algorithm for Maximal Monotone Operators［J］.Math Program，1992(55)：293－318

［8］GONG C，TEBOULLE M.A Proximal－based Decomposition Method for Convex Minimization Problems［J］.1994，64(1－3)：81－101

［9］徐以汎，吴芳.A Decomposition Method for Convex Minization Problems and its Application［J］.Acta Mathematice Application sinca，2001(17)：20－28

［10］HE B S，XU M H，YUAN X M.Solving Large－scale Least Squares Semidefinite Programming by Alternating Direction Method［J］.SIAM J Matrix Anal Appl，2011，32(1)：136－152

［11］XU M H，WU T.A Class of Linearized Proximal Alternating Direction Methods［J］.Optim Theory Appl，2011，151(2)：321－337

A Class of Modified Linear Proximal Alternating Direction Methods for Convex Optimization

LI Hui

(College of Mathematics，Chongqing Normal University，Chongqing 401331，China)

In this paper，the liner constraints of the original literature is extended to nonlinear constraints.Approximate Solution alternating decomposition algotithm is used，and a new type of nwdified linear proximal alternating direction method is proposed with theoretical analyses and algorithm comparison.

Proximalalternatingdirectionmethod；NonlinearconstrainedConvexprogramming； Decomposition methods；Linearized；Augmented Lagrangian

O221

A

1672－058X(2015)04－0023－05

10.16055/j.issn.1672－058X.2015.0004.007

2014－06－03；

2014－09－19.

李慧(1990－)，女，四川广安人，硕士研究生，从事最优化理论与方法研究.