条件C下的伪不变单调准则
2015-05-16潘正涛向丽娟刘晓静
潘正涛,向丽娟,刘晓静
(1.重庆师范大学数学学院,重庆 401331;2.重庆师范大学图书馆,重庆401331)
条件C下的伪不变单调准则
潘正涛1,向丽娟,刘晓静2
(1.重庆师范大学数学学院,重庆 401331;2.重庆师范大学图书馆,重庆401331)
在条件C下,推导出伪不变凸单调与严格伪不变凸函数之间的关系.
伪不变凸;广义不变凸;条件C
广义凸在数学、管理科学、工程学、经济学和最优化理论等领域中都发挥着重要的作用,不变凸函数和不变凸单调又是研究广义凸性的重要组成部分,文献[1-5]研究了关于广义不变凸与不变凸单调,文献[3]在条件C下,建立了伪不变凸单调与伪不变凸函数之间的关系.此处在条件C下,推导出伪不变凸单调与严格伪不变凸函数之间的关系.
1 预备知识
设Γ是Rn中的非空子集,η:Γ×Γ→Rn的向量值函数,F:Γ→Rn的向量值函数,θ:Γ→R上可微函数.
定义1[3]称集合Γ是关于η不变凸的,若存在η:Rn×Rn→Rn,使得对任意x,y∈Γ,λ∈[0,1],有
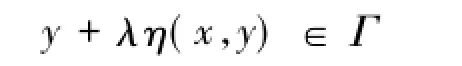
定义2[3]设Γ⊆Rn是关于η不变凸的,称F:Γ→Rn是关于η在Γ⊂Rn上的严格伪不变单调,如果对任意不同的两点x,y∈Γ,有
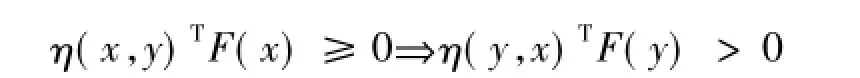
定义3[1]设Γ⊆Rn是开集,函数θ:Γ⊆Rn→Rn映射,有
(a)称θ是伪不变凸单调函数,若存在η:Γ×Γ→Rn,使得对任意x,y∈Γ⊆Rn,有
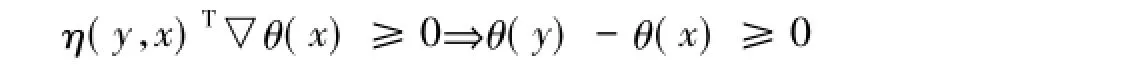
(b)称θ是严格伪不变凸单调函数,若存在η:Γ×Γ→Rn,使得对任意x,y∈Γ⊆Rn,x≠y,有

条件C[3]设η:X×X→Rn,则对任意x,y∈Rn,且对任意λ∈[0,1],有
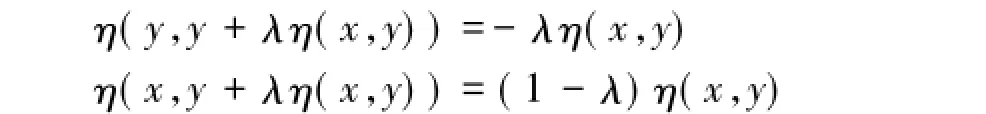
注:由条件C,有

事实上,很容易通过以下证明得到
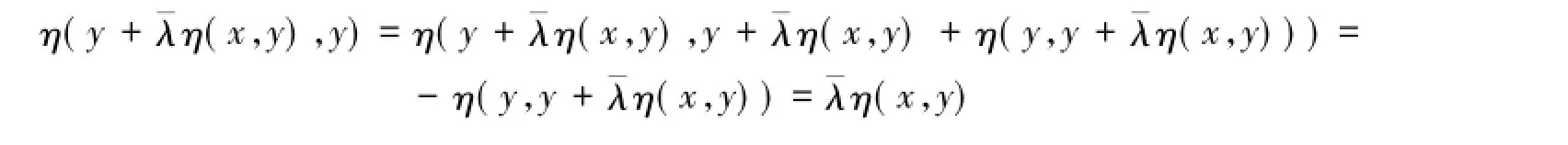
2 主要结果
定理1若
1)Γ⊂Rn是关于η的开不变凸集;
2)η满足条件C;
4)▽θ是关于η在Γ上的伪不变凸单调.
则θ是关于η在Γ上的严格伪不变凸函数.
证明设x,y∈Γ,x≠y,有

需要证明

反证法:假设


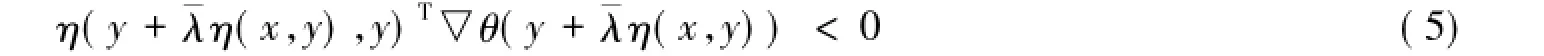


式(7)与式(2)矛盾,因此θ是关于η在Γ上的严格伪不变凸函数.
[1]RUIZ GARZON G,OSUNA-GOMEZ R,RUFIAN-LIZANA A.Generalized Invex Monotonicity[J].European Journal of Operational Research,2003(144):501-512
[2]YANG X M,YANG X Q,TEO K L.Criteria for Generalized Invex Monotonicities[J].European Journal of Operations Research,2005(164):115-119
[3]YANG X M,YANG X Q,TEO K L.Generalized Invexity and Generalized Invariant Monotonicity[J].Journal of Optimization Theory and Applications,2003(117):607-625
[4]PENG J W.Criteria for Generalized Invex Monotonicities without Condition C[J].European Journal of Operations Research,2006(170):667-671
[5]张其茂.一类B-预不变凸目标规划的最优性充分条件[J].重庆工商大学学报:自然科学版,2009,30(6):522-525
Quasi-invex Monotone Norm Under Condition C
PAN Zheng-tao1,XIANG Li-juan,LIU Xiao-jing2
(1.College of Mathematics Science,Chongqing Normal University,Chongqing 401331,China 2.Library,Chongqing Normal University,Chongqing 401331,China)
Under condition C,this thesis presents the relationship between quasi-invex monotone and strict quasi-invex functions.
quasi-invexity;generalized invex;Condition C
O177
A
1672-058X(2015)04-0018-02
10.16055/j.issn.1672-058X.2015.0004.005
2014-07-28;
2014-09-25.
潘正涛(1989-),男,重庆长寿人,硕士研究生,从事向量优化理论及应用研究.
