一类特殊的Bezout矩阵*

吴梅

(安徽大学数学科学学院，合肥 230601）

一类特殊的Bezout矩阵*

吴梅

(安徽大学数学科学学院，合肥 230601）

介绍了一类特殊的Bezout矩阵，即分裂Bezoutian，并总结了分裂Bezoutian的相关性质；对B－型分裂Bezoutian中元素表示的迭代关系式给予了证明；并建立了B－型分裂Bezoutian与一类特殊的Hankel矩阵之间的联系.

Bezout矩阵；分裂Bezoutian；Hankel矩阵

Bezout矩阵是由某一域上任意两个多项式生成的一类特殊的方阵，是一类对称矩阵.在对Bezout矩阵的研究过程中产生了许多深刻的结论，例如Barnett型分解公式［1］以及三角分解公式［2］.正是由于Bezout矩阵自身性质的特殊性和优良性，使得它在多项式惯性、稳定性问题以及控制理论、系统理论等方面都有着重要的应用［3－6］.此处将根据Bezout矩阵的相关性质，对分裂Bezoutian这一特殊Bezout矩阵进行初步的探讨和研究.

1 预备知识

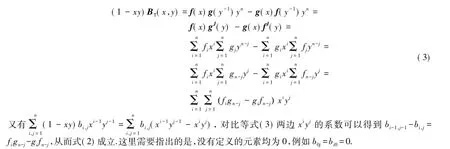
引理1如果An是对称(反对称)Toeplitz矩阵的逆，或是中心对称(中心反对称)T+H－Bezoutian的逆，则An可以表示成两个特别的T+H－Bezoutian B+和B－的和，即An＝B++B－，且An的生成多项式可以表示如下：

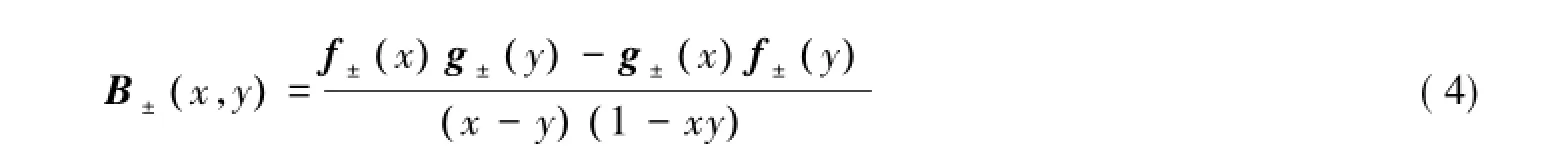
其中，f+，g+∈Fn+2是对称向量，f－，g－∈Fn+2是反对称向量.

2 分裂Bezoutian的定义、元素表示和基本性质

定义1用多项式的语言来表述转换Λ：Fn×n→F（n+2）×（n+2)

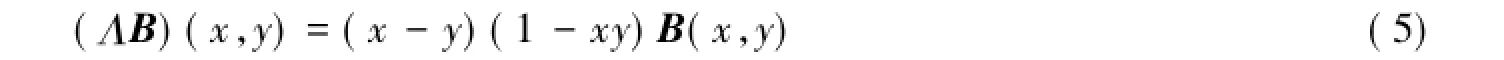
矩阵B∈Fn×n称为分裂Bezoutian，若存在向量f，g∈Fn+2都是对称(反对称)的，使得式(6)成立

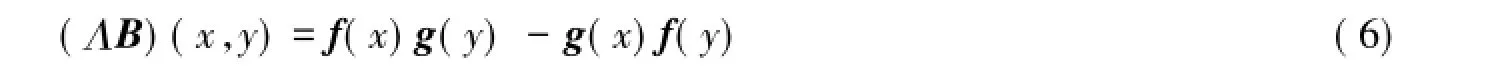
这里分裂Bezoutian Bs记作Bs(f，g).

2.1 元素表示

由分裂Bezoutian Bs的对称性质可知，Bs的全部元素可以较容易获得.若

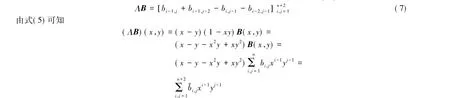
比较xi－1yj－1系数可得式(7)成立.

2.2 基本性质

2.2.1 线性性

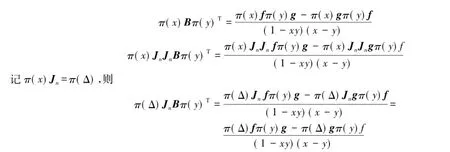
即可得到JnB＝B，同理可得BJn＝B.f，g为反对称向量时，可用同样方法证明之.

3)由上述结果可得，BJ＝JBJ＝B.

2.2.3 三角分解公式

分裂Bezoutian B可以表示成两个下三角、上三角Toeplitz矩阵乘积之和，即满足三角分解公式.

3 B－型分裂Bezoutian元素表示的迭代关系式以及其与之间的联系

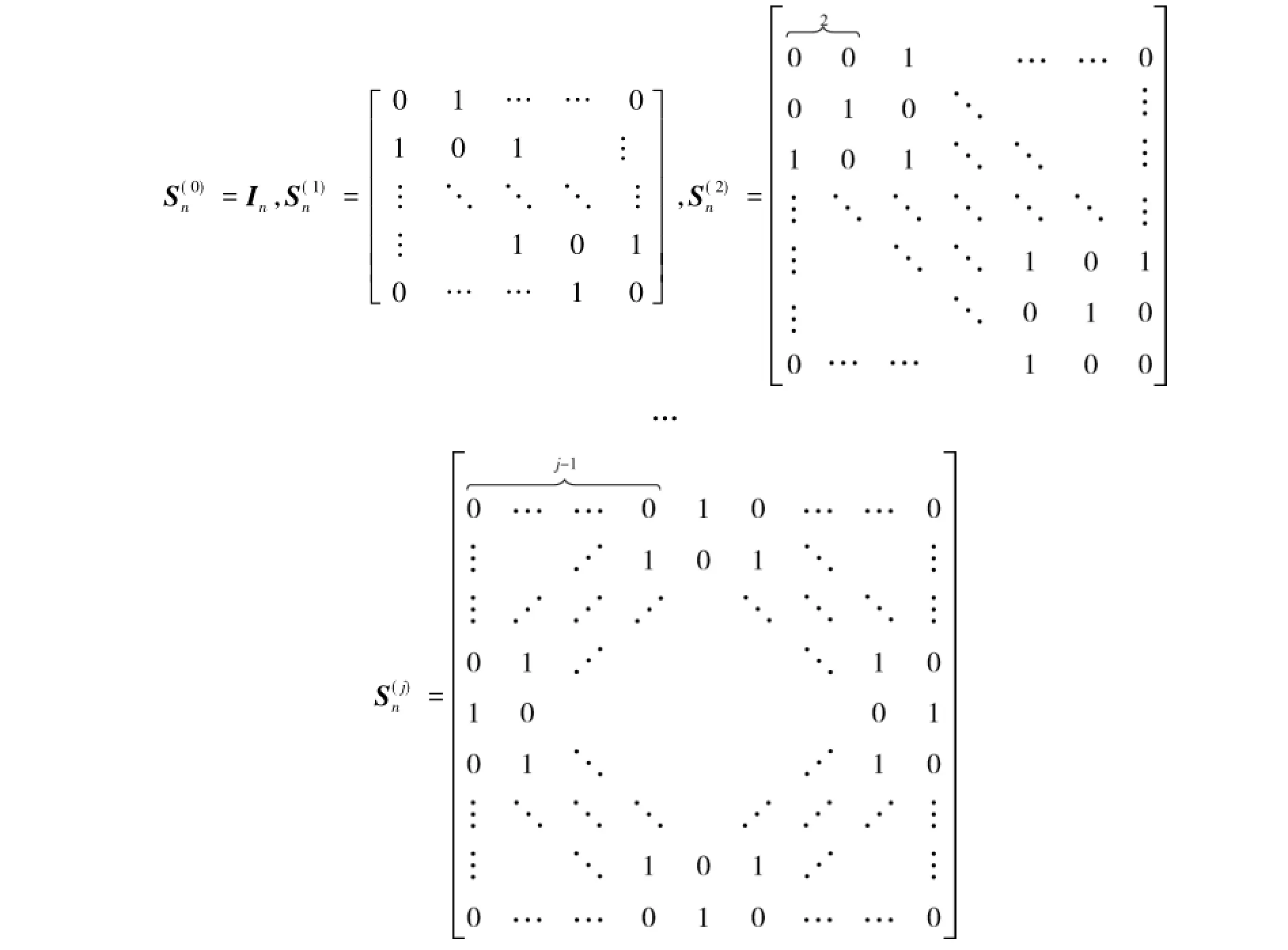
上标j表示第一行中第一个非零元素之前的零元素的个数.

证明由已知条件知

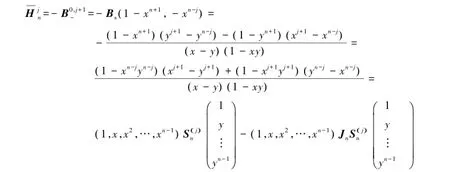
从而式(9)成立，同理可以证明式(10)的成立.

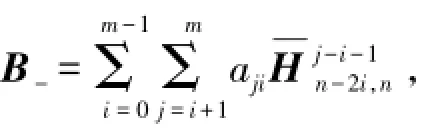
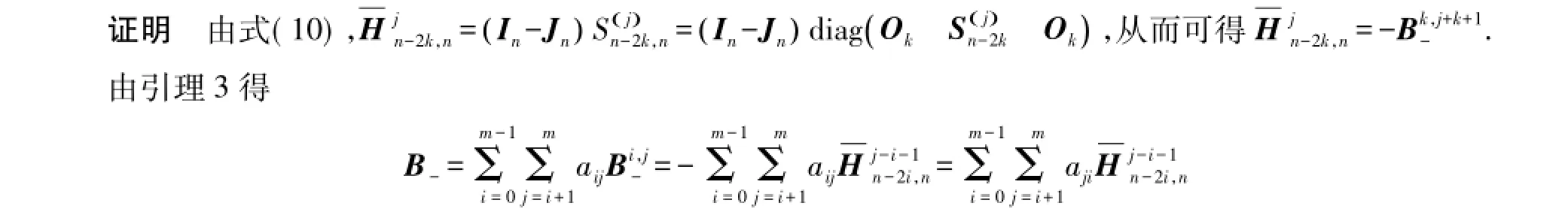
故定理2得证.

［1］BARNETT S.A Note on the Bezoutian Matrix［J］.SIAM J Appl Math，1972(22)：84－86

［2］YANG Z H，CUI B F.On the Bezoutian Matrix for Chebyshev Polynomials［J］.Applied Mathematics and Computation，2012，219(3)：1183－1192

［3］BARNETT S.Polynomials and Linear Control Systems［M］.New York：Marcel Dekker，1983

［4］HELMKE U，FUHRMANN P A.Bezoutians，Linear Algebra and its Applications［J］.1989，22(124)：1039－1097

［5］LANCASTER P，ROST M.Algebraic Methods for Toeplitz－like Matrices and Operators［J］.Operaror Theory，Bikha..user，Basel，1984(13)：402－410

［6］GOVER M J，BARNETT S.A Generalized Bezoutian Matrix［J］.Linear Multilinear Algebra，1990(27)：33－48

［7］VLASTIMILták.Explicit Expressions for Bezoutians［J］.Linear Algebra and its Applications，1984(59)：43－54

［8］刘冰，张羽乾.Bernstein－Bezoutian矩阵的若干性质［J］.重庆工商大学学报：自然科学版，2011，28(4)：339－442

A Special Class of Bezout Matrix

WU Mei

(School of Mathematical Sciences，Anhui University，Hefei 230601)

Firstly this paper introduces a special class of Bezout matrix named split Bezoutian and summarizes its properties.Secondly the proof on the recursion relation in split Bezoutian of B－type is obtained.Finally the relation between split Bezoutian of B－type and a special class of Hankel matrixS(j)nis constructed.

Bezout matrix；split Bezoutian；Hankel matrix

O241

A

1672－058X(2015)04－0001－05

10.16055/j.issn.1672－058X.2015.0004.001

2014－07－04；

2014－09－25.

安徽省自然科学基金(1208085MA02).

吴梅(1990－)，女，安徽六安人，硕士研究生，从事矩阵与算子理论研究.