数值模拟大气边界层中解决壁面函数问题方法研究

方平治，顾明，谈建国，韩志惠

(1.中国气象局上海台风研究所，上海 200030; 2.同济大学土木工程防灾国家重点实验室，上海 200092;3.上海市气象科学研究所，上海 200030)

数值模拟大气边界层中解决壁面函数问题方法研究

方平治1，顾明2，谈建国3，韩志惠3

(1.中国气象局上海台风研究所，上海 200030; 2.同济大学土木工程防灾国家重点实验室，上海 200092;3.上海市气象科学研究所，上海 200030)

在雷诺平均N－S方程湍流模型框架内，壁面函数常用来模型化壁面附近的低雷诺数流动。探讨基于标准湍流模型数值模拟大气边界层中出现的壁面函数问题。在已有标准壁面函数基础上，通过增加一个附加项来模型化地表上面建筑结构等粗糙元由于大小不一、错乱分布对地表附近空气流动产生的附加影响。通过模拟缩尺比为1∶300的具有较大空气动力学粗糙长度的中性大气边界层，以及缩尺比为1∶50的TTU低矮建筑模型在中性大气边界层内的绕流，对附加项的有效性和使用场合进行评估和说明。结果表明:附加项对于解决壁面函数问题，即在计算域内保持来流边界条件是必要的。

大气边界层;标准壁面函数;壁面函数问题;物理粗糙高度;空气动力学粗糙长度

重现中性大气边界层为计算风工程的基本要求［1］。数值模拟方法精度不仅受钝体绕流复杂性影响，数值模拟建筑结构所在大气边界层的不足也是重要因素。在无建筑结构的计算域中，源于中性大气边界层的来流边界条件应在整个计算域流向方向保持一致。Richards等［2］发现来流边界条件与建筑结构前来流间存在差异。基于标准k－ε湍流模型，Richards等［3］提出数值模拟中性大气边界层的4个经典假设; Richards等［4］对数值模拟中性大气边界层的基本理论进行更普适研究，并论述边界条件、湍流模型及壁面函数三者间相互关系。

基于雷诺平均N－S方程的湍流模型通常采用两种方法处理壁面附近的低雷诺数流动，即壁面函数法与近壁面模型法。前者采用标准壁面函数［5］;后者主要增加壁面附近的网格精度，但会增大计算量。Craft等［6－7］提出解析壁面函数。与前述两方法不同，解析壁面函数假定壁面附近的湍流粘性发生变化，通过直接积分控制方程求解壁面附近的低雷诺数流动。Miles等［8］通过直接模拟设置在建筑结构前的粗糙元获得来流边界条件。以上各种方法中，壁面函数法因在保证精度的同时兼具经济性、有效性，广泛用于工程中。然而，壁面函数问题，即在计算域地面附近，来流边界条件与建筑结构前来流间存在差异，因在模拟具有较大空气动力学粗糙长度的大气边界层中经常出现而使大气边界层的模拟精度受到影响［9］。

数值模拟中性大气边界层时，相容的来流边界条件函数表达式同样具有重要作用。为满足标准k－ε湍流模型的控制方程，文献［3］的湍动能来流边界条件的函数表达式为常数。而据文献［10－11］研究结果，湍动能在地面附近沿高度变化并存在峰值。Yang等［12］对相容性重新研究，给出与实际观测结果相吻合的湍动能来流边界条件函数表达式，并用于其它基于雷诺平均N－S方程的k－ε湍流模型中［13］。

基于标准k－ε湍流模型，本文给出在模拟中性大气边界层中解决壁面函数问题方法。该方法强调在已有标准壁面函数基础上导出的附加项的重要作用。本文方法及所有数值计算在商用CFD软件Ansys 13中实现。本文在回顾CFD中常用标准壁面函数基础上，导出附加项用于模型化地表面粗糙元因大小不一、错乱分布对地表附近空气流动产生的附加影响;通过分别模拟缩尺比为1∶300的具有较大空气动力学粗糙长度的中性大气边界层、缩尺比为1∶50的TTU低矮建筑模型在中性大气边界层内的绕流，对附加项的有效性及使用场合进行评估、说明，并对本文方法进行评价及总结。

1 标准壁面函数及附加项

在计算风工程中，通常采用基于雷诺平均N－S方程的湍流模型及壁面函数方法模拟壁面附近的低雷诺数流动。ρu*z/μ≥100时，壁面附近的流动常用对数律模拟［14］，其中z为至壁面距离，u*为摩擦风速，ρ为空气密度，μ为空气动力粘性系数。

对光滑壁面，对数律为

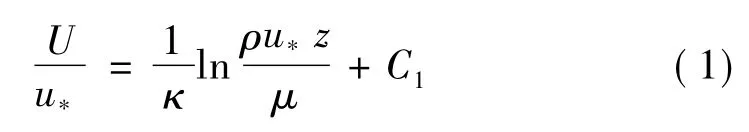
式中:U为流向平均风速;κ=0.42为冯·卡门常数［3］; C1=5.5。

对粗糙壁面，对数律为

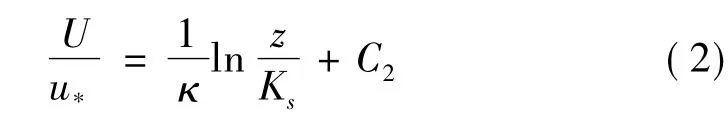
式中:Ks为物理粗糙高度，表示粗糙度;C2为常数。

据式(1)，标准壁面函数［5］为

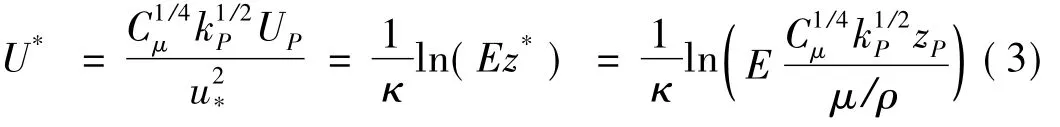
式中:U*为无量纲风速;kP为壁面第一层网格中心P点处湍动能;UP为P点风速;z*为无量纲距离;zP为P点至壁面距离;Cμ为模型常数;E=9.79。

对由大小相等、分布均匀的砂粒型粗糙元形成的粗糙壁面，在标准壁面函数基础上，据式(2)，修正的壁面函数［15］为

在商用CFD软件如Ansys 13中，要求Ks≤zP。然而工程应用中，中性大气边界层对应的Ks通常大于数值计算的zP，从而导致壁面函数问题［9］。在标准壁面函数基础上，通过引入新的附加项δB，可一定程度上解决该问题。γ=1时式(9)退化为式(4)。附加项δB也可认为是ΔB的一部分，故δB无新意，但式(9)提供了解决壁面函数问题的思路。

2 具有较大空气动力学粗糙长度的中性大气边界层模拟

据我国建筑结构荷载规范［16］，同济大学在TJ－2大气边界层风洞中分别对缩尺比1∶300的A、B、C、D类四类风场进行模拟［17］。因C、D类风场具有较大空气动力学粗糙长度z0，在数值模拟中需采用本文方法，即以具有最大空气动力学粗糙长度的D类风场为例说明其应用。模型风场的z0=6.756×10－3m(对应实际风场z0=2.0 m)，取参考高度zR=1.0 m，对应参考风速为UR=5 m/s。

2.1 CFD模型与计算方案

缩尺计算域的大小为12×1.5 m(Lx×Lz)，其中x表示流向方向，z表示竖向方向，见图1。采用非均匀结构化网格方案划分计算域网格，地面附近沿高度方向网格最小尺寸为0.01 m(由此给出zP=0.005 m)，流向方向网格尺寸为0.03 m，网格总数为24 000。速度－压力耦合方式为SIMPLEC，对流项的离散格式为QUICK，压力插值方式为PRESTO，所有计算方案的数值实现方法可参考Ansys 13的帮助文件。

2.2 边界条件

图1为入流面、出流面、顶面及地面位置处所用边界条件，该边界条件名称源于Ansys 13。各边界条件数学意义见表1。平均风速及湍动能来流边界条件源于同济大学TJ－2风洞模拟缩尺比1∶300的D类风场。湍动能k=0.5σu2，其中σu为流向脉动风速均方根值。计算中设局部地区湍流处于平衡状态，即ε=Ck∂U/∂z，湍动能沿高度变化［12］。由于模型风场的z0=6.756 ×10－3m，即使据Ks=20z0［9］，该模型风场的物理粗糙高度Ks也远大于zP=0.005 m。因此，需在标准壁面函数后添加附加项δB解决此矛盾。上述方法采用Ansys 13的用户自定义壁面函数实现。为强调附加项δB的重要性，用户输入值Ks=0.005 m，该值为地面附近网格能允许的最大值。

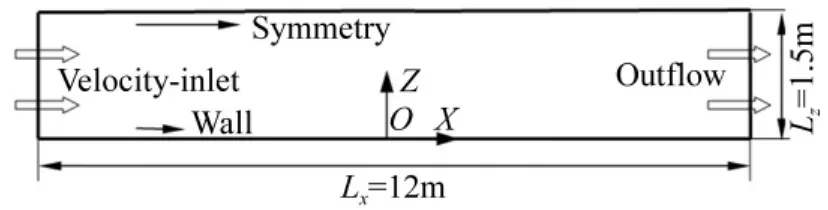
图1 O－XZ坐标系、缩尺计算域及边界条件Fig.1 Coordinate system O－XZ，scaled computational domain and boundary conditions

表1 具有最大空气动力学粗糙长度风场的边界条件及数学意义Tab.1 Boundary conditions and their corresponding mathematical implications in simulating the neutral ABL with the largest aerodynamic roughness length

2.3 湍流模型常数及附加项δB对地面附近流动影响

在标准k－ε湍流模型中共5个湍流模型常数，即Cμ，σk，σε，C1ε，C2ε;其中Cμ为最重要的模型常数，其余均与Cμ有直接或间接关系。各模型常数的计算方法见文献［3，12］。据C=u/k，Cμ由来流边界条件决定。由于标准k－ε湍流模型中Cμ为常数，而k沿高度变化，因此须寻找一高度对应的k值获得合适的Cμ及其它湍流模型常数。图2的计算结果表明，模型常数Cμ=0.23，σε=0.77，σk=0.59，C1ε=1.44，C2ε= 1.92及δB=5.5时，来流边界条件可获得较好模拟。由于在计算域流向方向来流边界条件均保持较好，用于比较的计算结果来源于出流边界位置处。

为说明附加项的重要性，模型常数不变、δB=0.0及3.0时计算结果见图2。由图2看出，δB较小时与来流边界条件相比，地面附近的平均风速偏大;湍动能被低估。平均风速偏大原因为δB较小时壁面第一层网格中心P点处UP偏大。换言之，文献［15］的修正壁面函数不能提供较小平均风速UP，从而导致计算域来流边界上的来流边界条件及计算域内建筑结构前的来流出现差异。δB=0时即为修正的壁面函数式(4)的计算结果。此时γ=1。可见，为模拟D类风场或为模拟具有较大空气动力学粗糙长度的风场，须采用附加项。

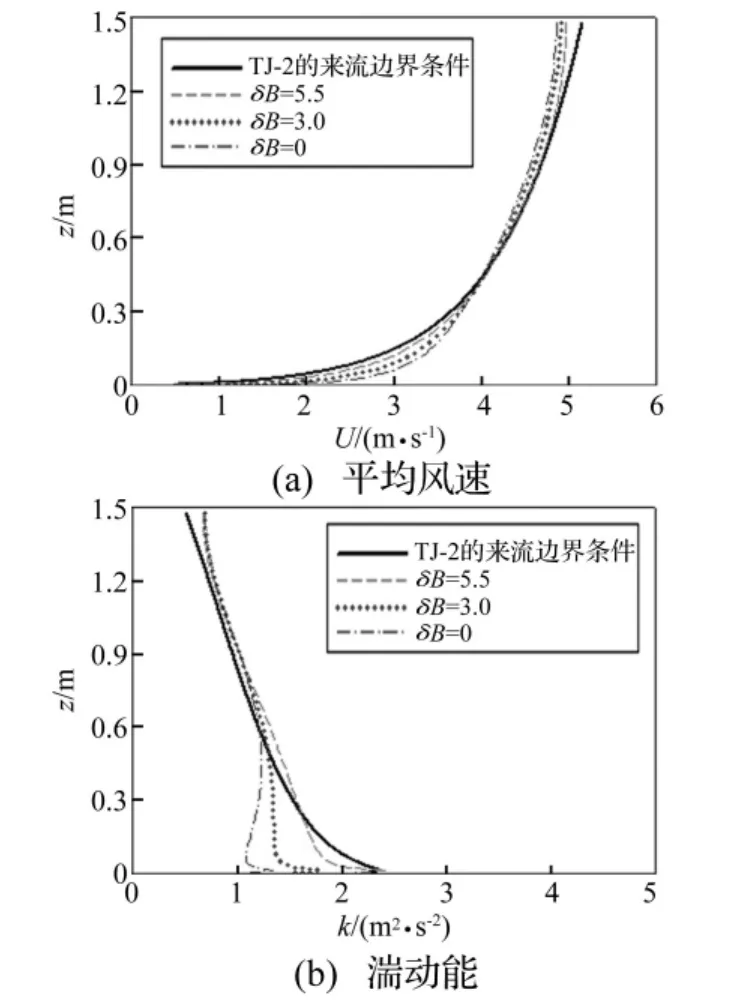
图2 附加项δB对地面附近流动影响Fig.2 Effects of the additional term δB on the flow near the land surface

31 ∶50缩尺比TTU低矮建筑模型绕流模拟

3.1 TTU建筑模型与缩尺比风场简介

TTU建筑模型常用于对风洞试验、数值模拟两种方法有效性验证［18］。在TJ－2风洞缩尺比1∶50的B类风场条件下，罗攀［17］对TTU建筑模型在不同风向角条件下的绕流进行研究。TTU模型、风向角定义及横截面测点位置见图3。本文对60°及90°风向角条件下绕流进行数值模拟。缩尺比1∶50风场对应的空气动力学粗糙长度为z0=0.001 58 m(实际风场z0=0.08 m)。取参考高度HR=1.0 m、参考风速UR=6 m/s。相同地貌不同缩尺比的模型风场对应的空气动力学粗糙长度不同。对缩尺比1∶300的B类风场无需附加项，但对缩尺比为1∶50时，则需在标准壁面函数中含附加项。

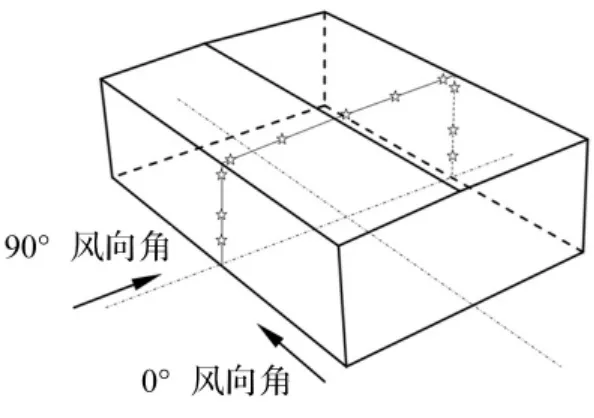
图3 TTU模型、风向角定义及横截面上测点位置Fig.3 TTU model，definition of the wind azimuth and positions of the measurement points on the edge of the cross section

3.2 CFD模型、计算方案及边界条件

文献［19］详细考察了计算域对数值计算结果影响。本文计算域在流向、横向及垂直方向尺寸分别为－6H≤x≤20H，－10H≤y≤10H，0≤z≤7H，见图4 (a)，其中H为缩尺TTU模型高度。地面附近第一层网格尺度0.008 m，对应zP=0.004 m，见图4(b)。计算域的入流面、出流面、顶面、侧面、地面及TTU模型表面边界条件(名称源于Ansys 13)见表2。标准k－ε湍流模型常数为Cμ=0.13，σε=1.02，σk=0.78，C1ε= 1.44及C2ε=1.92。为较好模拟该模型风场，须在标准壁面函数中用附加项δB=4.5。用户输入量Ks=0.004 m，为zP=0.004 m允许最大值。

3.3 数值模拟、风洞试验与现场实测结果对比

定义风压系数为

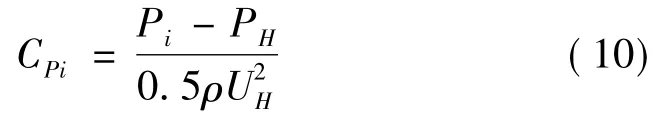
式中:Pi为测点平均压力;PH为TTU模型屋顶高度处静压;UH为未受扰动的来流平均风速;ρ=1.225 kg/m3为空气密度。

图5为模型横截面各测点平均风压系数的数值模拟结果、风洞试验结果及现场实测结果比较。图5(a)为在迎风面屋檐处，采用二阶QUICK格式标准k－ε湍流模型(SKE)计算结果。由于降低了湍动能在屋檐处的堆积［20］，MMK k－ε湍流模型(MMK)结果较满意。需要说明的是，SKE及MMK两湍流模型的控制方程及模型常数均相同。对图5(b)中绕流更复杂工况，因数值粘性降低，采用三阶MUSCL格式的MMK k－ε湍流模型结果亦较满意。由图5看出，数值模拟结果与风洞试验结果更接近，可能在数值计算中，由于采用附加项，风场模拟的得好，故风洞试验结果更接近数值计算结果。

表2 缩尺比1∶50的TTU模型绕流计算域边界条件及数学意义Tab.2 Boundary conditions and their corresponding mathematical implications in simulating the flow around the TTU model in a neutral wind field with the scale of 1∶50

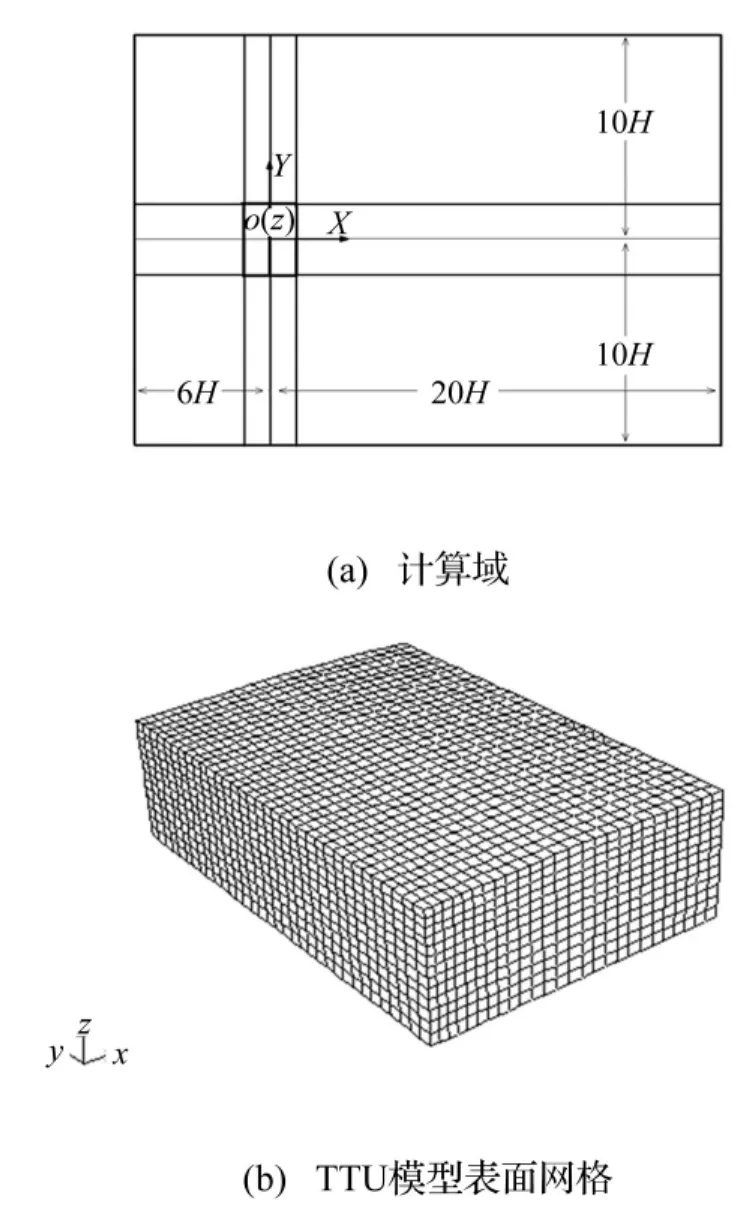
图4 风向角为90°时计算域、O－XYZ坐标系、TTU模型在计算域内位置及TTU模型表面的网格Fig.4 Scaled computational domain for the wind azimuth at 90 degree，O－XYZ coordinate system and location of the TTU model and the mesh on the TTU model surface

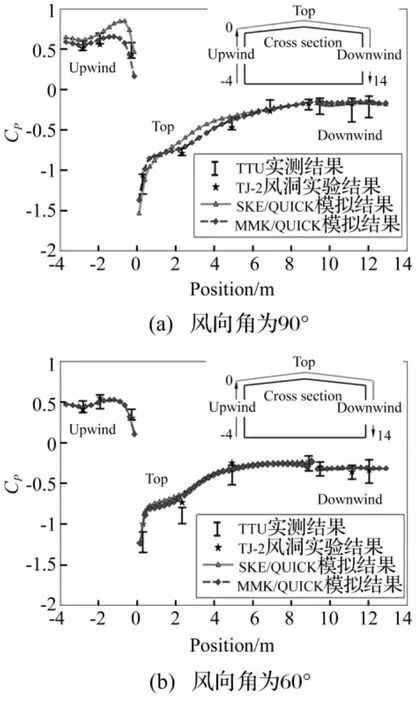
图5 横截面各测点平均风压系数的数值模拟结果、风洞试验结果和现场实测结果比较Fig.5 Comparisons of the mean pressure coefficients at the measurement points among the numerical，wind tunnel and real－site results:wind azimuth at 90 degree and wind azimuth at 60 degree

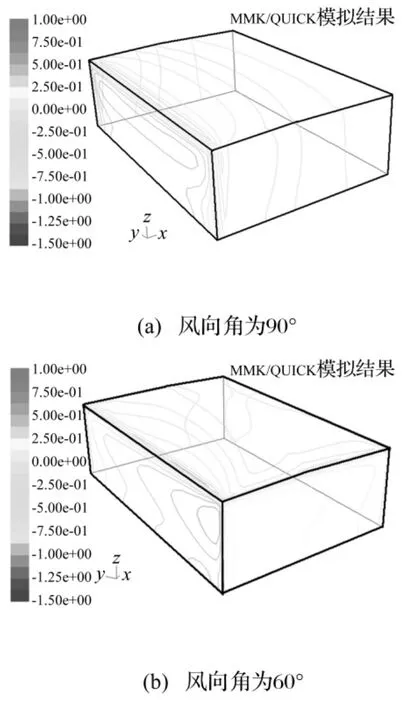
图6 TTU模型表面风压系数的数值模拟结果Fig.6 Numerical results of the pressure coefficients on the TTU surface:wind azimuth at 90 degree and wind azimuth at 60 degree

需要指出的是，本文数值风场参考高度HR=1.0 m对应参考风速为UR=6 m/s，该风速相对较低。据计算流体动力学中关于无量纲尺度z*=ρu*zP/μ定义，若忽略雷诺数影响，在z*保持不变条件下，低风速可采用较大网格尺度，从而降低计算量。对较复杂的建筑群数值模拟，可考虑低风速从而降低计算量［21］。不同工况条件下TTU模型表面风压系数分布见图6。由图6可见，对90°风向角工况，在迎风面屋檐及墙角处，由于分离流、风压系数变化较剧烈，且风压系数沿横截面对称分布;对60°风向角工况，由于出现三角翼涡，加剧了漩涡脱落的复杂性，其风压系数变化更复杂。

4 结论

(1)本文对基于标准k－ε湍流模型数值模拟大气边界层中的壁面函数问题进行研究。商用CFD软件中通常要求Ks≤zP;而对模拟具有较大空气动力学粗糙长度的大气边界层，Ks通常大于zP。该矛盾为出现壁面函数问题的根本原因，从而导致计算域地面附近的来流边界条件及建筑结构前的来流出现差异。通过分析，用附加项δB模型化地表上面建筑结构等形成的粗糙元因大小不一、错乱分布对地表附近空气流动产生的附加影响。

(2)通过模拟缩尺比1:300具有较大空气动力学粗糙长度二维中性大气边界层及缩尺比1:50的TTU低矮建筑模型在三维中性大气边界层内绕流，对附加项的有效性及使用场合进行评估、说明。结果表明，由于能在计算域的流向方向保持来流边界条件，附加项能有效解决壁面函数问题。本文参考风速较低，TTU建筑模型计算表明不影响计算结果可靠性;且对较复杂建筑群数值模拟，低风速可降低计算量。

［1］Jensen M.The model law for phenomena in the natural wind［J］.Igenioren(International Edition)，1958，2:121－128.

［2］Richards P J，Younis B A.Comments on“prediction of the wind－generated pressure distribution around buildings”by E H Mathews［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，34(1):107－110.

［3］Richards P J，Hoxey R P.Appropriate boundary conditions for computational wind engineering models using thek－εmodel［J］.JournalofWindEngineeringandIndustrial Aerodynamics，1993，46/47:145－153.

［4］Richards P J，Norris S E.Appropriate boundary conditions forcomputational wind engineering models revisited［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99: 257－266.

［5］Launder B E，Spalding D B.The numerical computation of turbulent flows［J］.Computer Methods in Applied Mechanics and Engineering，1974，3(2):269－289.

［6］Suga K，Craft T J，Iacovides H.An analytical wall－function for turbulent flows and heat transfer over rough walls［J］. International Journal of Heat and Fluid Flow，2006，27(5): 852－866.

［7］Craft T J，Gerasimov A V，Iacovides H，et al.Progress in the generalization of wall－function treatments［J］.International Journal of Heat and Fluid Flow，2002，23(2):148－160.

［8］Miles S，Westbury P.Practical tools for wind engineering in the built environment［J］.QNET－CFD Network Newsletter，2003，21:11－14.

［9］Blocken B，Stathopoulos T，Carmeliet J.CFD simulation of the atmospheric boundary layer:wall function problems［J］. Atmospheric Environment，2007，41(2):238－252.

［10］ESDU.Engineering sciences data item 85020［S］.EngineeringSciencesDataUnit，251－259RegentStreet，London，1985.

［11］Hargreaves D M，Wright N G.On the use of the k－εmodel in commercial CFD software to model the neutral atmospheric boundary layer［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95(5):355－369.

［12］Yang Y，Gu M，Chen S，et al.New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering［J］. Journal of Wind Engineering and Industrial Aerodynamics，2009，97(2):88－95.

［13］Yang W，Quan Y，Jin X Y，et al.Influences of equilibrium atmosphere boundary layer and turbulence parameter on wind loads of low－rise buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(10/11):2080－2092.

［14］普朗特，等.著.郭永怀，等.译.流体力学概论［M］.北京:科学出版社，1981.

［15］Cebeci T，Bradshaw P.Momentum transfer in boundary layers［M］.New York:Hemisphere Publishing Corporation，1977.

［16］GB50009－2001，中华人民共和国国家标准:建筑结构荷载规范［S］.

［17］罗攀.基于标准模型的风洞试验研究［D］.上海:同济大学，2004.

［18］Levitan M L，Mehta K C，Vann W P，et al.Field measurements of pressures on texas tech building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1991，38(2/3):227－234.

［19］方平治，顾明，谈建国，等.阻塞率对表面风压系数影响的数值模拟［J］.建筑科学与工程学报，2013，30(3): 101－106.

FANG Ping－zhi，GU Ming，TAN Jian－guo，et al.Numerical simulation of effect of blockage ratio on facade pressure coefficient［J］.JournalofArchitectureandCivil Engineering，2013，30(3):101－106.

［20］Murakami S，Mochida A，Kondo K，et al.Development of new k－ε model for flow and pressure fields around bluff body［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，66/67:169－182.

［21］方平治，史军，王强，等.上海陆家嘴区域建筑群风环境数值模拟研究［J］.建筑结构学报，2013，34(9):104－111.

FANG Ping－zhi，SHI Jun，WANG Qiang，et al.Numerical study on the wind environment among tall buildings in Lujiazui zone［J］.Journal of Building Strucutures，2013，34(9): 104－111.

Method to solve the wall function problem in simulation of atmospheric boundary layer

FANG Ping－zhi1，GU Ming2，TAN Jian－guo3，HAN Zhi－hui3
(1.Shanghai Typhoon Institute of China Meteorological Administration，Shanghai 200030，China;
2.State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China; 3.Shanghai Institute of Meteorological Science，Shanghai 200030，China)

Wall function is preferred to model the low Reynolds－number flow near wall based on the Reynoldsaveraged Navier－Stokes turbulent models.Then wall function problem in simulating the atmospheric boundary layer based on the standard turbulent model was investigated.An extra term which considers the extra effects induced by non－uniform and irregular distribution of rough elements such as various structures on the land surface was proposed and appended to the widely accepted standard wall function.The effectiveness and application situation of the proposed term were demonstrated by simulating a neutral wind field with the scale of 1:300 featured by larger aerodynamic roughness length. The flow around the TTU model in a neutral wind field with the scale of 1:50 was then simulated.The extra term is shown to be necessary to solve the wall function problem，i.e.，the preservation inlet flow boundary conditions in computation domain in both cases

atmospheric boundary layer;standard wall function;wall function problem;physical roughness height; aerodynamic roughness length

O353.1

A

10.13465/j.cnki.jvs.2015.02.015

2013－11－08修改稿收到日期:2014－02－14

方平治男，博士，副研究员，1974年生

顾明男，博士，教授，博士生导师，1957年生

邮箱:migngu@tongji.edu.cn