电感耦合等离子发射光谱(ICP)测定铅笔涂层中可迁移元素不确定度评定
2015-05-13任强
任 强
江西省产品质量监督检测院,南昌 330029
电感耦合等离子发射光谱(ICP)测定铅笔涂层中可迁移元素不确定度评定
任 强
江西省产品质量监督检测院,南昌 330029
电感耦合等离子发射光谱(ICP)测定学生用品(铅笔)中可迁移元素(铅、镉、铬、锑、钡和硒),考虑到测试重复性、称量误差、标准物质、容量瓶误差、测试设备、温度变化引入的不确定度的影响,对测量结果进行评定。
电感耦合等离子发射光谱(ICP);可迁移元素;不确定度
学生用品(铅笔)中可迁移元素是学生用品安全通用要求中的重要指标之一,通过对学生用品(铅笔)可迁移元素的测定,辨别学生用品(铅笔)的优劣程度。本文通过对学生用品(铅笔)中可迁移元素的测定不确定度数学模型,结合测定结果及其他因素合成不确定度并对影响其测定的不确定度的分量进行数学分析。
1 方法原理及步骤
1)称量:采用机械刮削方法(不刮取基体材料)从测试样品上获得0.9857g铅笔涂层测试试样,将试样置于150mL碘量瓶中。
2)提取:在碘量瓶中加入50mL、温度为37℃±2℃的c(HCl)=0.07mol/L的盐酸溶液与样品混合。将混合物避光,在温度为37℃±2℃时搅拌1h,然后在37℃±2℃放置1h。接着使用滤膜过滤器将混合物中的固体物有效分离出来,得到测试所需的样品溶液。同时做空白实验。
3)分析:校准曲线取6个浓度点,每个浓度点进样3次,以强度值对样品浓度绘制工作曲线,外标法定量。用ICP测试样品溶液中各元素的含量,计算材料中可溶性元素的含量。
2 计算公式和数学模型
样品中重金属含量即为被测量,报告要求结果用每千克样品中含重金属的质量来表示:

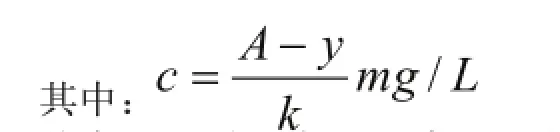
y:校准曲线的截距
k:校准曲线的斜率
A:消解溶液中金属的强度值
3 测量不确定度来源分析
产生不确定的因素通常包括检测仪器、实验环境、标准物质、前处理方法、人员操作和分析方法。本次评定主要考虑A类不确定度(测试重复性的标准偏差)和B类不确定度(包括天平误差和分辨率引入的不确定度、标准物质引入的不确定度、容量瓶误差引入的不确定度、测试设备引入的不确定度、温度变化引入的不确定度等)。
4 各分量标准不确定度的评估
4.1 样品质量的测量不确度
天平型号:Mettler-Toledo AL204电子天平。
根据电子天平计量检定证书,电子天平的不确定度为0.18mg。
称量0.9857g样品质量的相对标准不确定度为:

4.2 定容体积V引起的不确定度
铅笔涂层中可溶性有害元素分析采用50mL容量瓶,其体积不确定度一般有:容量仪器误差、测量重复性、实验室温度波动三个影响分量。
4.2.1 容量仪器误差:50mL容量瓶在20℃的体积为50±0.05mL,为均匀分布,其引入的标准不确定度为:

4.2.2 测量重复性:由于充满容量瓶的变化引起的不确定度可通过该容量瓶的典型样品的重复性实验来评估。对典型的50mL容量瓶充满10次并称量的实验,得出A类不确定度:
s=0.01mL
4.2.3 温度波动:根据制造商提供信息,该容量瓶已在20℃校准,而实验室的温度在±5℃之间变动。该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容量瓶的体积膨胀,因此,只需考虑前者即可。水的体积膨胀系数为2.1×10-4℃-1,因此产生体积变化为:
±(50×5×2.1×10-4)= ±0.052mL
计算标准不确定度时假设温度变化为均匀分布,即:


表2 定容体积V的测量不确定度来源及其分量计算
合成标准不确定度为:

相对标准不确定度为:

4.3 样品溶液重金属浓度的ICP测量不确定度
采用ICP—OES进行玩具有害元素分析,一般先通过对空白溶液和系列标准溶液测定,根据测得的响应值,仪器按最小二乘法线性回归,建立回归方程并绘制工作曲线,然后对样品溶液直接测定后可自动计算出待测元素浓度。其不确定度主要来源有:工作曲线的非线性、标准溶液浓度值、待测溶液测量重复性。
4.3.1 工作曲线的非线性引入的不确定度urel(c),各元素浓度与强度的关系见表3。

表3
利用表3中数据用一元线性回归拟合校准曲线方程为Y=a×c+b,相关系数为r,溶液浓度c的标准不确定度u(c)由下式求得:

校准回归直线斜率α、截距b、相关系数r以及在校准曲线上测得的样品的各元素含量见表4。
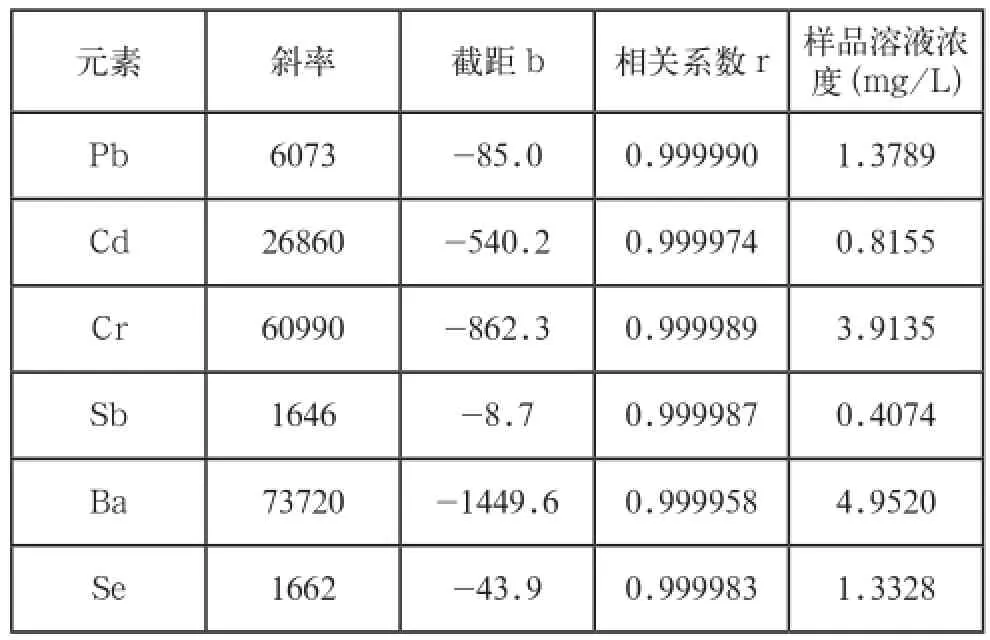
表4

将各元素标准点测试3次(p=3),每个元素共测了5种不同浓度的溶液测定3次,则n=5×3=15,连同校准曲线斜率α、截距b一起代入上述公式计算,结果见表5。

表5
4.3.2 标准工作溶液浓度值引入的不确定度Urel(Std)
各元素国家标准溶液均购自国家标准物质中心,其中Pb、Cd、Cr、Ba、sb、Se的浓度均为1000mg/L。依据标准溶液证书提供的不确定度和标准溶液稀释采用的容量体积不确定度可计算0.25mg/L标准工作溶液的相对标准不确定度Urel(Std),结果见表6所列。本文以0.25 mg/L Pb标准工作溶液的相对标准不确定度为例,计算如下:
国家标准物质研究中心生产的1000 mg/L Pb单元素标准溶液,其标准物质证书扩展不确定度为0.2%,按正态分布B类评定可得到相对标准不确定度为:0.2% ÷3=0.067%。实际测量时,将国家标准物质研究中心生产的1000mg/LPb单元素标准溶液稀释配制成100mg/ L工作液,用10mL移液管吸10mL入l00mL容量瓶得100 mg/L Pb标准溶液,稀释后的100 mg/L标准溶液的相对标准不确定度为:
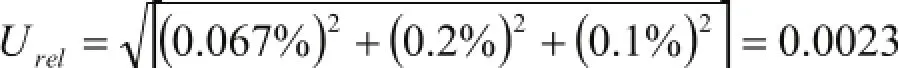
式中,0.2%为10mL移液管相对标准不确定度,0.l%为100mL容量相对标准不确定度。
再次稀释400倍得0.25 mg/L Pb标准工作溶液,其相对标准不确定度为:

式中,0.6%为1mL加液器吸液相对标准不确定度,0.1%为100mL 容量相对标准不确定度。
依据上述计算方法计算,得出各元素标准工作溶液浓度值引入的不确定度urel(Std)结果见表6。
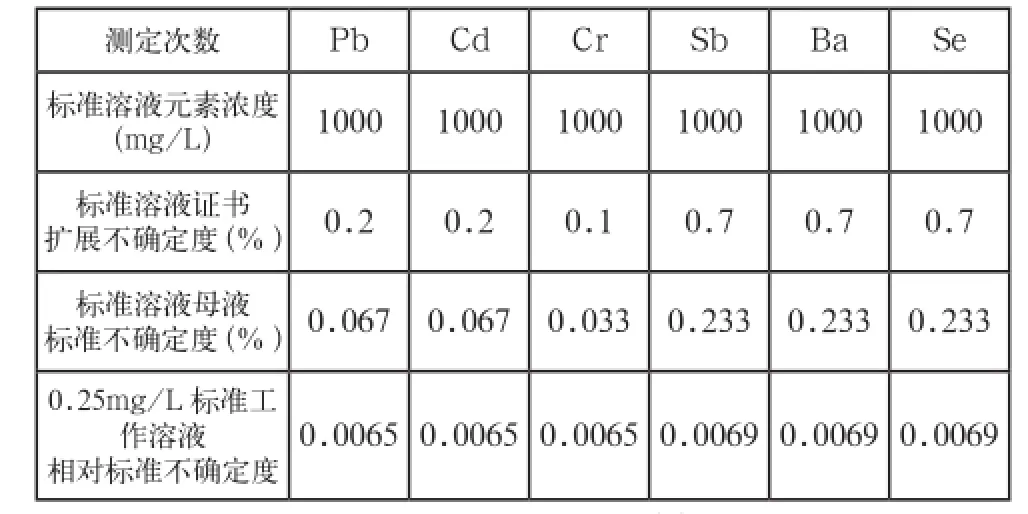
表6 各元素标准工作溶液浓度值引入的不确定度
4.3.3 待测溶液测量重复性urel(r)
测定值的不确定性主要来源于仪器本身的精密度和稳定性。采用PE 7300DV(ICP-OES)对样品进行6次重复性测试,测定数据呈正态分布,按A类评定,根据贝塞尔法计算,结果见表7。

表7 待测溶液测量重复性不确定度urel(r)
样品溶液重金属浓度的ICP测量不确定度计算公式为:
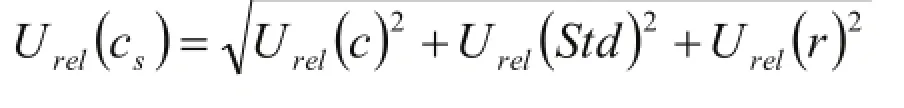
将工作曲线的非线性引入的不确定度urel(c)、标准工作溶液浓度值引入的不确定度urel(Std)和待测溶液测量重复性不确定度urel(r)代入上述公式计算,得出样品溶液重金属浓度的ICP测量不确定度,见表8。

表8 样品溶液重金属浓度的ICP测量不确定度
5 不确定度的合成及扩展
按下述公式对以上分量进行合成,得相对合成标准不确定度:

按国际惯例,取包含因子k=2,则测量结果的相对扩展不确定度为下表所列:

测定次数PbCdCrSbBaSe Urel,mg/kg0.02700.06060.02160.11420.02200.0348
6 结束语
通过采用电感耦合等离子发射光谱(ICP)测定学生用品(铅笔)中可迁移元素,并对测定方法不确定度的产生原因进行了分析,完成了不确定度的评定,避免了分析过程中存在的不利因素对检测结果的影响。
[1] GB 21027-2007《学生用品的安全通用要求》
[2] GB 6675.4-2014《玩具安全 第四部分:特定元素的迁移》
