云南省1958-2013年极端降水时空变化特征分析*

杨晓静，徐宗学，2，左德鹏，2，刘 琳

（1.北京师范大学水科学研究院，水沙科学教育部重点实验室，北京100875；2.全球变化协同研究中心，北京，100875）

云南省1958-2013年极端降水时空变化特征分析*

杨晓静1，徐宗学1，2，左德鹏1，2，刘 琳1

（1.北京师范大学水科学研究院，水沙科学教育部重点实验室，北京100875；2.全球变化协同研究中心，北京，100875）

利用云南省1958-2013年28个气象站日降水数据，计算了9个极端降水指数。基于Mann-Kendall（MK）方法进行趋势分析，滑动t检验（MTT）、Mann-Kendall、Pettit三种方法进行突变检验，小波分析、反距离权重法则分别探讨极端降水指数周期特性及空间分布特征。结果表明：①时间上，中小雨及连续降水日数均减小，极端降水量则显著增加，1958-2013年全省年降水量以-11.8 mm／10a的速率减少；较能反映降水均值特征的指数（CDD、R10、R20、PRCPTOT）未发生突变，而能反映极端降水变化特征的指数（CWD、R95p、R99p、SDII）的突变分别发生于2002、1993、1980、1994年左右；周期变化上，除CDD、R99p、SDII（周期分别为18年、14年、8年）外，其余指数的周期大小及其变化过程均较为相似，对应周期均为8年左右。②空间上，除CDD、CWD、SDII、PRCPTOT外，其余指数总体时空变化趋势较为一致。对比云南省5个气象地理分区降水，滇中降水量处于中等偏下水平，但该地区遭受极端干旱、极端降水风险高于其他地区，而其他地区极端降水与年平均降水量的空间分布特征较为一致。

极端降水指数；趋势；周期；突变；空间分布；云南

气候变化在过去几十年中一直是气象科学、水文科学研究中最重要的课题，全球变暖已引起世界各地学者的广泛关注［1］。早期限于高质量日气象要素数据的可获取性，全球及区域范围内气候变化研究都主要集中于长期气候事件均值变化特征，而极端气候事件对社会、经济及环境的影响远大于气候变化均值产生的影响［1-2］。在全球变暖背景下，大气湿度增加、雷暴及大范围的暴雨增强，导致极端降水事件的发生频率显著增加［3］。而经济社会发展过程中的降水被认为是最重要的气象要素，对供水、河川径流、作物产量、自然植被均具有重要的意义；此外，极端降水事件通常易引发一系列极端水文事件（如：干旱、洪涝），对主要经济来源是农业的国家和地区影响尤为显著［4-5］。

目前的研究对极端降水事件发生频率、强度变化规律给予了充分关注，与国外已有研究相比，我国针对极端降水事件的研究起步相对较晚。Alexander等［6］利用10个极端降水指数分析全球极端降水特征，结果表明20世纪以来全球极端降水总体呈增加趋势，亚洲局部地区则与之相反，且局地降水特征差异明显。Zhang等［7］利用中东地区15个国家52个站点数据，分析计算了11个极端降水指数，结果表明降水日数、降水强度及日最大降水均呈减小趋势，且均未体现空间相关性；对比加拿大、美国、意大利、澳大利亚等国家／地区研究结果同样表明不同地区极端降水发生频率、强度、持续时间等方面差异明显［4，8-10］。张宁［11］对我国1951-2005年极端降水时空分布特征进行了研究，结果表明平均降水强度与降水日数全国范围内基本一致，分别呈增加、减少趋势；且1970年代末以后极端降水事件处于增加趋势，尤其是1990年代末，极端降水强度以及频数增加较快，存在10年左右的周期。王志福［12］在全国尺度上对极端降水事件的频率及强度特征作了分析，结果表明全国持续1 d极端事件空间上表现为全国大部分上升、华北和西南等地呈下降的趋势。持续2 d以上极端事件全国平均的趋势不显著，而区域之间差异明显。我国目前除了对全国尺度极端降水特征的研究，在流域尺度及省／市范围的研究也较多，且选用的评价方法存在明显差异［13-17］，极端降水指标主要包括绝对阈值指标和百分位阈值指标、结合区域特点定义的极端降水指标。研究不同区域尺度极端降水特征为更好应对气候变化具有十分重要的意义，而目前针对云南省极端降水方面的研究相对我国其他地区偏少，已有研究主要针对该省局部地区平均降水特性［18-20］。尽管Li等［21］分析了1960-2012年云南省极端降水的变化趋势，但并未对极端降水可能存在的突变、周期等进一步研究。

云南是一个农业大省，地处我国西南边陲，是一个以低纬高原山地为主的省份，地形条件极为复杂且受季风气候影响显著［22］。由于受高原季风气候的影响，该区异常天气条件和天气极端变化易形成农业气象灾害，且生产方式较为落后，气象灾害对农业造成的损失最大。因此，开展云南省极端降水时空分布特征研究具有十分重要的现实意义。本文基于云南省28个气象站点1958-2013年逐日降水数据，从气候变化检测专家组（Expert Team on Climate Detection）推荐的极端降水指数中选取其中9个指数。从时间上，分析极端降水可能存在的趋势、突变及周期特性；从空间上，揭示极端事件演变特征。

1 资料与方法

1.1 资料及分区

利用中国气象科学数据共享服务网（http：／／cdc.cma.gov.cn／home.do）提供的中国地面气候资料日值数据集（V3.0），选取1958-2013年云南省28个气象站日降水数据。并对选用的降水数据进行严格审核及一致性检验，筛查数据中的异常值并插补缺测部分。为便于空间分布对比，参照中国气象地理区划［23］将云南省分为5个区，即：滇东北、滇东南、滇中、滇西北、滇西南，如图1所示。

1.2 方法

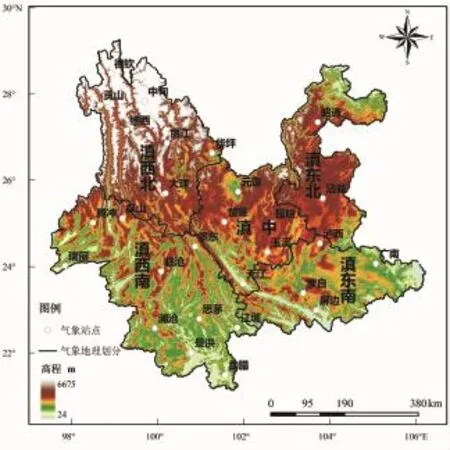
图1 云南省28个气象站点空间分布图

利用RClimDex（http：／／etccdi.pacificclimate. org／software.shtml）分别对28个气象站点降水数据进行质量控制，并计算文中选用的9个极端降水指数值，各指数及其分类详见表1。根据计算结果分析全省极端降水指数时间和空间分布特征，具体方法如下：时间变化上，文中选取常用Mann-Kendall（M-K）非参数检验法进行趋检验并用Sen’s法计算斜率［24］，Mann Kendall Tau、Spearman两种非参数方法进行相关性检验［25］。目前对极端降水突变现象的物理机制尚不明确，突变检验时应采用多种方法，同时选择合适的显著性水平［26］。为明确极端降水的突变特性，故采用常用的5年滑动t检验（5年MTT）、10年滑动t检验（10年MTT）、Mann-Kendall、Pettit这几种方法进行突变检验［26-28］。在分析降水趋势、相关性及突变特性基础上，选取代表性较强的极端降水指数基于复Morlet小波分析方法计算极端降水指数周期。周期分析前为消除小波变换的边界效应，对各极端降水指数值分别进行周期延拓处理，即在原始数据的前后各延长一个周期，对延拓后的数据进行小波变换后再截取对应原始资料的小波系数来分析［29］。空间变化上，选用云南年平均降水空间分布计算误差最小的反距离权重法［30］，基于Arcgis9.3对各极端气候指数进行插值计算，从而直观反映云南省极端降水主要空间分布特征。由于篇幅所限，上述不同方法计算公式及步骤详见文中引用的相关参考文献。

2 结果与分析

2.1 极端降水时间变化特征

2.1.1 极端降水指数趋势及相关性分析

2.1.1.1 站点变化趋势

分别对28个站点的9极端降水指数值进行趋势分析，结果表明：约71%～93%的站点无明显变化趋势，各站点极端降水指数趋势统计结果见表2（变化即通过显著性水平0.1检验）。其中持续干日（CDD）、强降水日降水量（R95p）、极强降水日降水量（R99p）、降水强度（SDII）呈增加趋势的站点数明显多于减少的站点数，持续降水日（CWD）、降水大于10 mm天数（R10）、降水大于20 mm天数（R20）、年降水量（PRCPTOT）则呈下降趋势。

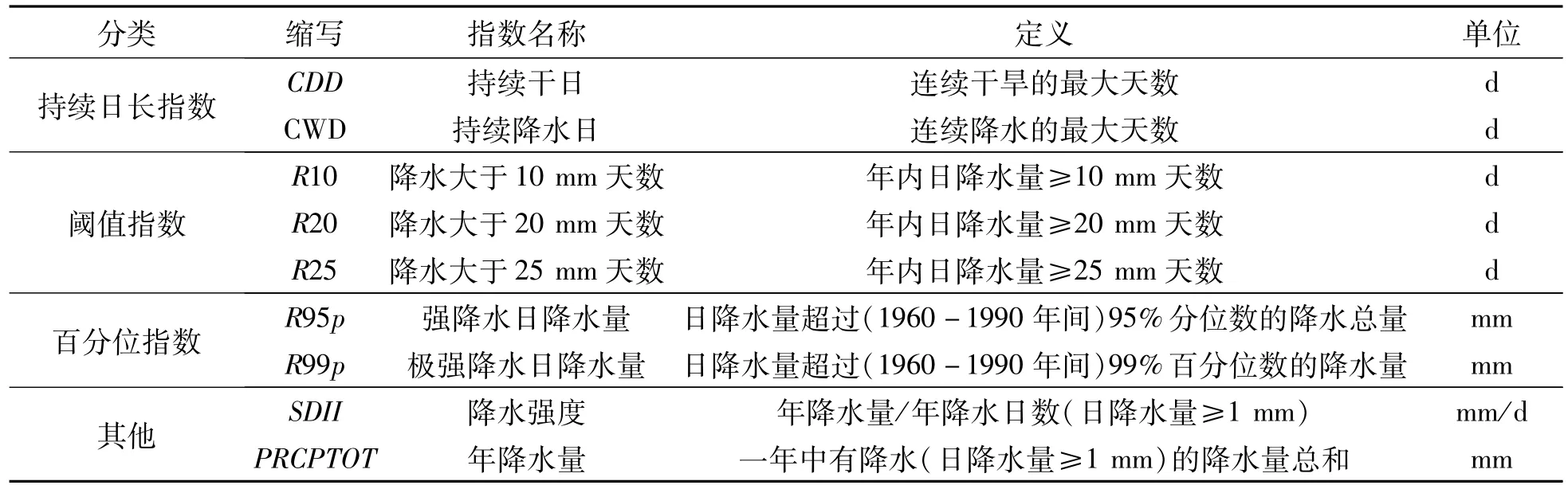
表1 极端降水指数定义

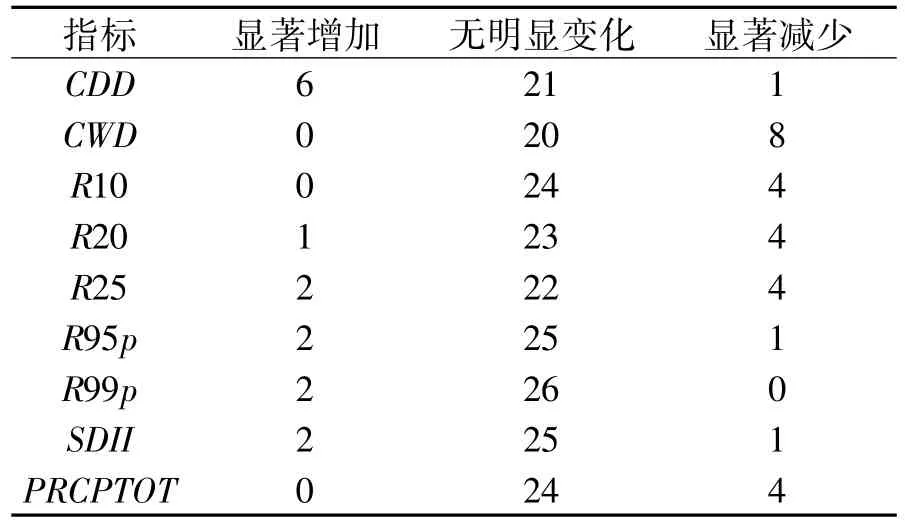
表2 1958-2013年极端降水指数变化趋势站点统计表

2.1.1.2 年平均变化趋势

根据文中选用的极端降水指数定义及计算方法将其分为4类（持续日长指数、阈值指数、百分位指数及其他），并利用Mann Kendall Tau、Spearman两种相关检验方法对各指数进行相关性分析。不同类别极端降水指数1958-2013年全省年平均值的主要特征如下所示。

（1）持续日长指数（CDD、CWD）

如图2所示，1958-2013年全省多年CDD平均值为52 d，其中最长达87 d（1963年），最小值33 d（1992年），以1 d／10年的速度增加，且2002年以来CDD明显增多。CWD多年平均天数仅为10 d，仅达CDD多年平均值的19.2%，而变化趋势呈显著减小（显著性水平为0.01），且2002年后减小趋势更为明显。相关性分析结果（见表3～表4）表明：CDD仅与降水强度（SDII）相关性显著（Mann Kendall Tau、Spearman检验所得的相关系数分别为0.226、0.327），而CWD则仅与CDD、SDII无显著相关性。

（2）阈值指数（R10、R20、R25）

1958-2013年间，R10、R20、R25多年平均值分别为36、16、11，小雨天数（365-CDD-R10）最多，而强降水天数明显多于中雨天数（R10-R20）。R10、R20均呈减小趋势，而R25则呈增加趋势。降水阈值指数主要根据日降水量进行区分，因此R10、R20、R25间存在显著相关性，R10与CDD、SDII无显著相关性，R20、R25则仅与CDD无关，相关系数值详见表3～表4（下同）。

表3 1958-2013年降水指数Kendall’s tau-b等级相关系数

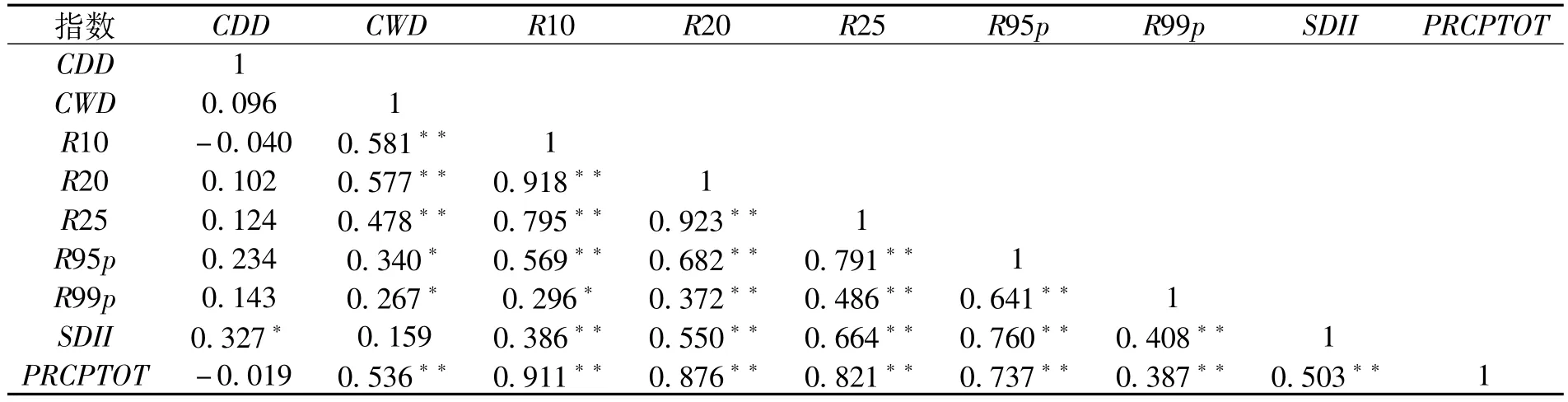
表4 1958-2013年降水指数Spearman相关系数

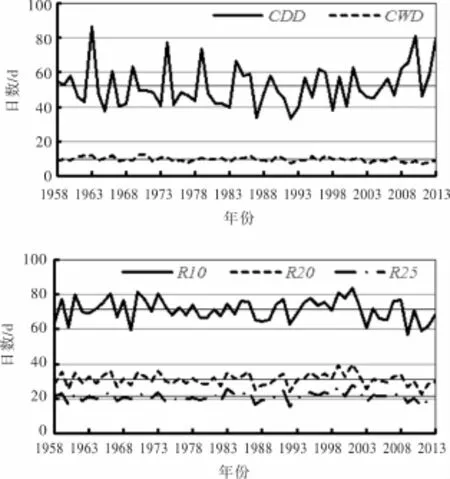
图2 1958-2013年云南省年平均极端降水指数（CDD／CWD／R10／R20／R25）变化趋势

（3）百分位指数（R95p、R99p）

如图3所示，强降水日降水量（R95p）多年平均值为269 mm，占近1／4的年降水量（PRCPTOT），且年际间差异明显，总体略为增加（0.84 mm／10年）。极强降水日降水量（R99p）多年平均值为79 mm，变化趋势显著（显著性水平0.05）并以3.1mm／10年的速度增加，对PRCPTOT贡献率在4%（2012年）到11%（1984、2002年）间变化。相关性分析结果表明R95p、R99p仅与CDD无显著相关性，均与其余极端降水指数相关性显著。

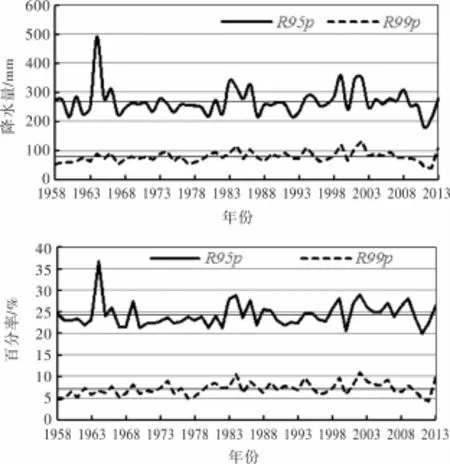
图3 1958-2013年百分位指数变化特征

（4）其他（SDII、PRCPTOT）

1958-2013年，SDII值在9.5-12.0 mm／年变化，变化趋势不显著。SDII仅与CWD相关性不显著，与R95p相关性最为明显。PRCPTOT多年平均值为1 104 mm，最大值为1 336 mm（1964年），最小值为903 mm（2009年），且以11.8 mm／10年的速度减少。相关系数的大小一定程度上能反映出阈值指数对PRCPTOT的不同贡献程度，PRCPTOT与R10相关系数最大，即反映出R10对PRCPTOT贡献程度最大。

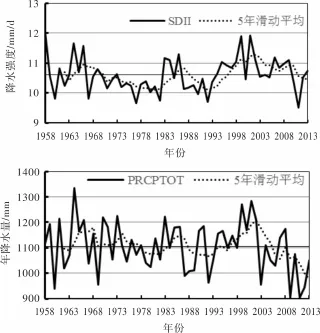
图4 1958-2013年PRCPTOT、SDII变化特征

综上所述，9个极端降水指数的全省年平均值变化差异明显，1958-2013年云南省持续干日（CDD）呈增加趋势，而持续降水日（CWD）日数则呈显著减小趋势。与此同时，全省年降水量（PRCPTOT）呈减少趋势，而降水强度（SDII）、极强降水日降水量（R99p）及日降水大于25 mm的日数均呈增加趋势。由此可见，极端降水指数的变化特征反映出云南省存在变干趋势，但其极端降水事件发生频率、持续日数及降水强度均明显增加。此外，为能用较少的指数较为全面反映极端降水的趋势、周期及空间变化特点，本研究优先选择无显著相关的极端降水指数进行进一步分析研究。由于各极端降水指数均基于降水数据进行计算，除SDII与CWD无显著相关关系，CDD仅与SDII显著相关，其余指数间均呈显著相关关系，因此建议在极端降水特征分析中必须采用的指数包括：CDD、CWD及SDII，其余指数则视需探讨的降水极端程度而定。

2.1.2 极端降水指数突变检验

由于各极端降水指数可能存在的突变年份不确定性较大，因此文中利用5年MTT、10年MTT、M-K及Pettit分别对9个极端降水指数进行了突变点检验，结果见表5。鉴于滑动t检验（MTT）能检测给定年数子序列突变情况，且结果中可能出现多个突变点。而M-K、Pettit两种方法则用于序列整体变化趋势检测，存在突变时结果中仅存在一个突变年份情况较多。因此，综合这几种常用突变检验方法计算的结果不但能判断出1958-2013年各极端降水指数整体变化趋势，同时也能发现其年代间存在的异常。

表5 突变检验结果

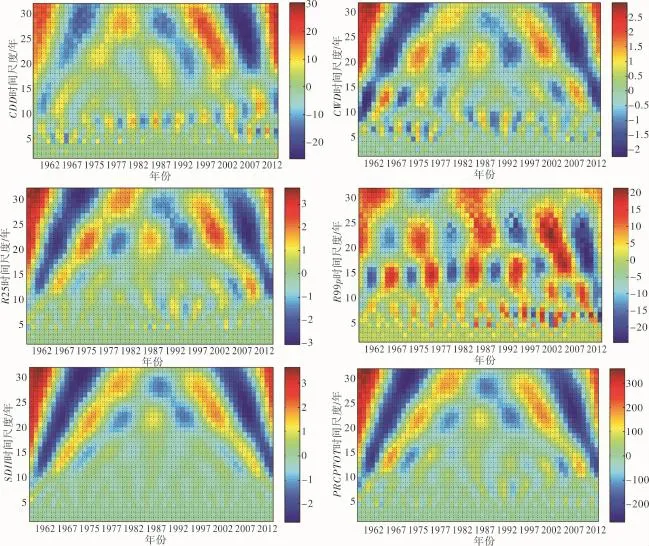
图5 Morlet复小波分析结果

（1）持续日长指数（CDD、CWD）

突变检验结果表明CDD无显著突变，整体呈增加趋势。3种突变检验方法均检出CWD在2002年发生突变，10年MTT反映出，2002年以来CWD呈显著减少趋势，据M-K突变检验结果CWD在2008年后减小趋势更显著（显著性水平为0.1），且2009年超出了0.05的显著性水平，该结果与云南省2009年来连续4年发生干旱的实情较为相符。

（2）阈值指数（R10、R20、R25）

MTT对阈值指数检验结果较为一致，5年MTT结果表明R10、R25均在1970年代初期、2002、2008年开始发生突变。10年MTT结果表明R10、R20、R25均在1990年代初及21世纪初期均开始发生突变。而M-K及Pettit对R10、R20均未检出突变点，仅M-K检测出R25在1982年发生显著突变。由此可说明阈值指数在1958-2013年间变化趋势总体上较为一致，而R25在1980年代后增加趋势较其他阈值指数更为显著。

（3）百分比指数（R95p、R99p）

5年MTT检验结果表明在1958-2013年间出现多个突变点，各突变开始的年份间相差5年，该结果可能受到算法及R95p年际间波动大的特点共同作用。10年MTT对R95p检出的突变点个数明显少于5年MTT，1993年后R95p发生显著变化，且与M-K检验结果一致。综合三种方法检验结果可得R99p在1958-2013年间，突变始于1980年代；年代上的突变特征即：1960年代初突变，其值呈减小趋势，1970年代初呈增加趋势，1980年代后减小趋势明显且在2006年左右呈增加趋势。由此可知，百分比指数年代间的波动特征显著，一定程度上反映出云南省极端降水事件年代变化特征不确定性较大的特点。

（4）其他（SDII、PRCPTOT）

SDII综合检验结果表明在1994年后发生了显著突变，年代尺度上的突变特征即：SDII在1970年代初和1990年代开始发生突变，2002年后呈增加趋势，该趋势与全球总体趋势一致［6］。5年MTT检验值反映出2008年后SDII存在略微增加趋势，PRCPTOT突变检验结果表明年降水量整体上无突变发生，在5年尺度上，2002、2008均发生突变，且结果表明2008年后PRCPTOT呈减少趋势，这与云南省2008年以来连续4年干旱少雨的情况较为相符。

综上所述，极端降水指数不同方法突变结果存在一定差异，但SDII、CWD的突变检验结果较为一致，突变年份分别为1994、2002年。突变检验方法不同易造成结果的不确定性，为得到更为客观的突变检验结果文中综合分析了不同方法的结果。结果表明：CDD未检出突变点，而R95p突变始于1990年代初，R99p与R25均始于1980年代初；较能反映年降水变化特征的降水指数（R10、R20与PRCPTOT）均未检验出突变，且在1958-2013年间其值均呈减小趋势，而综合滑动检验结果表明这三个指数均在2002、2008年发生了突变，且该结果与已有研究结果较为一致［19，31］。

2.1.3 极端降水指数周期分析

结合上文结果，筛选出相关性较低且变化趋势较为显著的极端降水指数进行周期分析（图5），即：CDD、CWD、R25、R99p、SDII、PRCPTOT。其中R99p与SDII能够反映极端降水强度变化特征，CDD与CWD能够反映极端事件持续日数，R25能够反映出极端降水事件发生频率，而PRCPTOT则能够反映年平均降水变化趋势。

结合复Morlet小波方差及其实部等值线图对周期进行分析，结果表明CDD 17-28年周期震荡能量最大，即周期变化最明显，而1960年代中期开始，明显呈现8年左右的周期。8年特征时间尺度上，CDD平均周期约为5年；28年时间尺度上，其平均周期即18年左右，呈现出4个“增-减”变化周期，且2005后CDD增加趋势明显（由于篇幅限制未列出特征周期过程线图，下同）。从图5中可看出，CWD、R25的小波方差图及小波实部等值线图变化特征较为相似，均呈4个“增-减”变化周期，且最明显的两个特征时间尺度均为：22年、13年，对应的周期分别为14年、8年左右。

相比持续日长指数及阈值指数（R25），百分位指数R99p的周期波动较大。R99p特征时间尺度为22年、15年、6年，对应的周期分别为14年、10年、4年，其中14年、10年周期波动及持续时间较长，周期过程线呈4个、5个“增-减”变化周期。SDII、PRCPTOT变化最明显的两个主周期均为28年、22年，且特征时间尺度对应的周期均相等（分别为18年、14年）。SDII第3主周期为15年，其过程线约以10年为周期发生变化。而PRCPTOT第3主周期为13年，对应特征过程线周期为8年。

综上所述，周期分析中除CDD、R99p、SDII外，其余指数周期值及变化过程均较为接近，对应周期分别为18年、14年、8年。由于数据系列长度限制，所得周期结果存在一定不确定性。为尽量能够得出较为可靠的周期分析结果，对小波分析结果进行非参数检验，给定99%置信水平，周期特点为CWD、R25、PRCPTOT在置信区间对应的周期均为8年左右，与全国极端降水存在10年左右振荡周期的结论较为接近［11］；CDD、R99p、SDII周期分别为5年、4年、8年左右。该结果从另一个侧面反映出了各指数间的相关程度，根据文中周期分析结果可得：结合CDD、CWD、R99p、SDII、PRCPTOT周期变化特征，即能较全面反映年降水、极端降水的周期变化特性。

2.2 极端降水指数空间变化特征

2009年10月以来，云南遭遇4年连旱，降水较之前多年平均值偏少，为能客观反映各指数年代变化特征，下文中涉及的年代变化趋势均与上一年代值比较而得。如图6（图中为区分年代起始年份，将1960年代表示为1961／1970，以此类推）所示，基于云南省气象地理分区各极端降水指数年代、空间变化特征表现在以下几方面。

（1）持续日长指数（CDD、CWD）

1958-2013年CDD多年平均与年代平均值在14～104间波动，年代及多年平均CDD空间分布整体由大到小即：滇西北、滇中、滇西南、滇东北、滇东南。1961-2010年的5个年代CDD变化趋势为增加→减少→减少→增加。CDD最大值核心区存在由滇西北向滇中地区移动的趋势，各地区最小值呈明显增大趋势。各年代分别与1958-2013年多年平均值相比得到：仅1980年代、1990年代小于多年平均值。

CWD相对CDD较小，1958-2013年间其值在5.4～20间波动。综合年代差异，滇西南地区CWD值最大，其余依次为滇西北、滇东南、滇中、滇东北。CWD在5个年代的变化趋势为减小→增加→减小→减小。CWD最大值的中心区从滇西南地区西北部向该区南部移动，呈减小趋势；最小值时间上变化趋势不明显，空间上变化趋势即：从滇东北地区向滇中地区延展。综上，持续日长指数时空变化特征明显，最为突出，即滇中地区CDD最大值及影响区域均呈增加趋势，CWD最小值影响范围也存在扩大趋势。与1958-2013年多年平均值相比可得：除1991／2000、2001／2010的CWD值小于多年平均值，其余均大于多年平均值。

（2）阈值指数（R10、R20、R25）

如图6（c）-（e）所示，R10、R20、R25值呈递减趋势，分别在16.3～72.1、4.1～39.1、1.8～29.5间波动，与1958-2013年多年平均值相比，除1960年代、1990年代值大于多年平均值外，其余均与多年平均值较为接近。云南省各地R10、R20值由大到小依次为滇西南、滇东南、滇西北、滇中、滇东北。R25除滇中地区值略大于滇西北地区值外，其余大小排列均与R10、R20一致。R10、R20在5个年代变化趋势为：减小→减小→增大→减小；R25变化即：减小→增大→增大→减小；阈值指数总体增减幅度均较平缓，但是滇中地区R20、R25在时间及空间上均呈增加趋势。

（3）百分位指数（R95p、R99p）

1958-2013年R95p、R99p值分别在99.3～578.3 mm、17.9～192.9 mm变化，且变化趋势相近；与1958-2013多年平均值比较结果一致，仅1981／1990、2000／2010值大于多年平均值。云南省各地区百分位指数值大小排列依次为滇西南、滇东南、滇西北、滇中、滇东北。年代间变化趋势均为减小→增加→减小→增加，百分位指数值最大的年代为21世纪初。空间上，R95p、R99p最小值区域主要集中在滇东北地区且年代际变化趋势不显著，而最大值区域由滇西北地区的东南部向该区其他部分延伸，呈增大趋势；与此同时，由图6（f）～6（g）中发现，除1970年代滇中地区百分位指数值减小外，其余年代均呈增加趋势。

（4）其他（SDII、PRCPTOT）

1958-2013年SDII值波动范围为：6.42～16.12 mm／d，仅1990年代、21世纪初大于该期间多年平均值；全省大部分地区值域在10.01～12.40 mm／d间，各地区值由大到小分别为：滇西南、滇东南、滇中、滇西北、滇东北；该值1961 -2010年间变化趋势为减小→增大→增大→增大，其中滇中地区除1970年代外均呈增加趋势。PRCPTOT值的变化范围在536.94～2294.05 mm，年代平均值与多年平均值均较为接近；相对其他指数该指数值域范围较广，滇西南地区PRCPTOT值最大，其余依次为滇东南、滇西北、滇中、滇东北；年代间变化趋势为减小→增大→减小→减小，以1958-2013年多年平均值相比，其值的增减幅度相对较小，且空间变化趋势不明显。SDII根据PRCPTOT值计算而得，空间分布上较为一致，但是年代变化却存在明显差异，即：指数值相对于上一个年代比较，1970年代后PRCPTOT呈减小趋势，而SDII的变化趋势则与之相反。

图6 1958-2013年云南省极端降水指数年代际空间分布图

综上所述，文中选用的指数除CDD、CWD、SDII、PRCPTOT外，其余指数总体时空变化趋势较为一致。除滇中地区外，全省其他地区各指数时空变化趋势与全省总趋势较为一致。云南极端降水年代际波动显著，而年代变化下年平均降水量空间差异性不明显。全省5个地理分区对比发现，滇中受地形地势、季风气候等因素共同作用下，降水量虽处于全省中等偏下水平，但该地区遭受极端干旱、极端降水风险高于其他地区，且在1958-2013年间极端干旱、极端降水事件发生频率及强度均呈增加趋势。

3 结论与讨论

近年云南省极端气候事件频发，文中根据日降水数据计算了9个极端降水指数（CDD、CWD、R10、R20、R25、R95p、R99p、SDII、PRCPTOT），并探讨了各指数趋势、周期及空间分布等特征。主要结论如下所示。

（1）趋势及相关性：全省1958-2013年能反映极端降水变化的指数（CDD、R25、R95p、R99p）及降水强度指数（SDII）均呈略微增加趋势，CWD、R10、R20、PRCPTOT呈略微下降趋势；其中，CWD、R99p的减、增趋势均通过0.05显著性水平。CDD仅与SDII显著相关，SDII则仅与CWD无显著相关性。全省年降水量以11.8 mm／10a的速率减少，此过程中小雨及无雨日数均减小。云南省存在变干趋势，而极端降水在发生频率、持续日数及降水强度均呈增加趋势。

（2）突变特性：1958-2013年间CDD、R10、R20、PRCPTOT未检出突变，CWD、R95p、R99p、SDII突变分别开始于2002、1993、1980、1994年左右；R25利用MTT检验的结果与R10、R20较为一致，M-K检验出其于20世纪80年代初发生突变。

（3）周期变化：除CDD、R99p、SDII外，其余指数周期大小及其变化过程均较为接近，对应周期分别为18年、14年、8年。99%置信水平下，周期特点为CWD、R25、PRCPTOT在置信区间对应的周期均为8年左右；CDD、R99p、SDII对应周期分别为5年、4年、8年左右。

（4）空间变化特征：云南极端降水年代际波动显著，而年代变化下年平均降水量空间差异性不明显。全省5个地理分区对比发现，年降水量由大到小依次为滇西南、滇东南、滇西北、滇中、滇东北。滇中地区遭受极端干旱、极端降水风险高于其他地区，且在1958-2013年间极端干旱、极端降水事件发生频率及强度均呈增加趋势，而其他地区极端降水与年平均降水量的空间分布变化特征较为一致。

（5）在极端降水指数选择上，目前极端降水指标较为丰富，不同地区可比性较差，而且部分指标相关性较强。分析极端降水特征时，建议先对拟采用的指标进行适用性分析，用最少的指标个数全面反映极端事件降水强度、持续日数及其发生频率。据文中分析结果，建议采用CDD、CWD、R25、R99p、SDII、PRCPTOT；突变检验方法的差异，易导致结果的不同，但是综合多种方法结果及已有研究成果能够得出较为可靠的突变检测结果；此外，在周期分析中受降水资料年份限制，周期结果中建议事先给定99%的置信水平，识别出可信度较高的潜在周期。

云南省气候类型多样，降水季节分布特征差异显著，且生物多样性、农业生产等方面易受降水影响。本文主要针对该省多年平均、年代及年际极端降水特征进行研究。趋势分析结果中可发现云南省持续干日呈增加趋势而持续降水日数则呈显著减少趋势，一定程度上反映出云南省农作物生长期间面临干旱的风险增大，与此同时也对保护生物多样性的工作提出了新的挑战；而极端降水指数在降水量上呈现出年平均降水量减小，降水强度、极端降水频率及其持续日数均呈增加趋势，其中R99p增加趋势显著。根据这一结果不难发现，云南省干旱风险增加的同时也面临着雨涝灾害增多的风险，这不仅会对日常生活产生影响，也对农业生产造成危害。如：强降水量的增加，云南省重要的经济作物烤烟的产量将受到严重影响；而突变检验中CDD、R10、R20、PRCPTOT未检出突变，这进一步明确云南省在提高抗旱能力的同时也需要提高城乡对极端雨涝事件的应对能力；文中极端降水指数周期分析的结果，可以为防洪抗旱工作提供一定的参考借鉴；典型极端降水指数空间分布特征表明滇西南地区极端降水事件发生可能性最大，滇中地区极端降水事件风险则呈增加趋势。由于滇西南地区是云南省生物多样性最为丰富的地区，随着极端事件的增多，该地区生物多样性的保护工作将更为艰巨。而滇中地区是云南省政治、经济及文化中心，为了保障该地区经济社会等健康有序发展，适当提高该区对极端降水事件的预报、预防及应对能力势在必行。此外，为了进一步明确该省降水特性并能为生产生活提供更强有力的科技支撑，建议结合气候变化特点从极端降水成因及极端降水季节变化特征等方面进一步深入探讨。

［1］ Wang Q，Fan X，Qin Z，et al.Change trends of temperature and precipitation in the Loess Plateau Region of China，1961-2010［J］.Global and Planetary Change.2012，92／93：138-147.

［2］ Peterson TC，Zhang X，Brunet-India M，et al.Changes in North American extremes derived from daily weather Data［J］.Journal of Geophysical Research：Atmospheres.2008，113（D7）：1-9.

［3］ Roy SS，Jr R C B.Trends in extreme daily precipitation indices in india［J］.International Journal of Climatology.2004，24（4）：457-466.

［4］ Dos Santos CA C，Neale CM U，Rao T V R，etal.Trends in indices for extremes in daily temperature and precipitation Over Utah，USA［J］.International Journal of Climatology.2011，31（12）：1813-1822.

［5］ Radinovic D，Curie M.Some evidence on European Monsoon existence［J］.Theoretical and Applied Climatology.2012，110（1／2）：11-15.

［6］ Alexander L V，Zhang X，Peterson T C，et al.Global observed changes in daily climate extremes of temperature and precipitation［J］.Journal of Geophysical Research：Atmospheres.2006，111（D5）：D5109.

［7］ Zhang X，Aguilar E，Sensoy S，et al.Trends in Middle East climate extreme indices from 1950 to2003［J］.Journal of Geophysical Research：Atmospheres.2005，110（D22）：D22104.

［8］ Acquaotta F，Fratianni S.Analysis on long precipitation series in Piedmont（North-West Italy）［J］.American Journal of Climate Change.2013，2：14-24.

［9］ Risbey JS，Mcintosh P C，Pook M J.Synoptic components of rainfall variability and trends in Southeast Australia［J］.International Journal of Climatology.2013，33（11）：2459-2472.

［10］Zhang X B，HoggW D，Mekis E.Spatial and temporal characteristics ofheavy precipitation events over Canada［J］.Journal of Climate.2001，14（9）：1923-1936.

［11］张宁.中国极端气温和降水趋势变化研究［D］.南京：南京信息工程大学，2007.

［12］王志福，钱永甫.中国极端降水事件的频数和强度特征［J］.水科学进展，2009，20（1）：1-9.

［13］李剑锋，张强，陈晓宏，等.新疆极端降水概率分布特征的时空演变规律［J］.灾害学，2011，26（2）：11-17.

［14］李丽平，章开美，王超，等.近40年华南前汛期极端降水时空演变特征［J］.气候与环境研究，2010，15（4）：443-450.

［15］任玉玉，任国玉.1960-2008年江西省极端降水变化趋势［J］.气候与环境研究，2010，15（4）：462-469.

［16］王萃萃，翟盘茂.中国大城市极端强降水事件变化的初步分析［J］.气候与环境研究，2009，14（5）：553-560.

［17］孙凤华，吴志坚，杨素英.东北地区近50年来极端降水和干燥事件时空演变特征［J］.生态学杂志，2006，25（7）：779-784.

［18］刘瑜，赵尔旭，黄玮，等.云南近46年降水与气温变化趋势的特征分析［J］.灾害学，2010，25（1）：39-44，63.

［19］王学锋，郑小波，黄玮，等.近47年云贵高原汛期强降水和极端降水变化特征［J］.长江流域资源与环境，2010，19（11）：1350-1355.

［20］于晓丽，马显莹，顾世祥，等.滇中高原区降水量50年的时空变化［J］.长江流域资源与环境，2013，22（Supp.1）：96-102.

［21］Li Y，He D，Hu J，etal.Variability of extreme precipitation over Yunnan Province，China1960-2012［J］.International Journalof Climatology，2015，35：245-258.

［22］陈宗瑜.云南气候总论［M］.北京市：气象出版社，2001：1.

［23］中国气象局预测减灾司.中国气象地理区划手册［M］.北京市：气象出版社，2006：54.

［24］Gocic M，Trajkovic S.Analysisof changes inmeteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia［J］.Global and Planetary Change.2013，100：172-182.

［25］Farlie D JG.The performance of some correlation coefficients for a general bivariate distribution［J］.Biometrika.1960，47（3／4）：307-323.

［26］魏凤英.现代气候统计诊断与预测技术［M］.2版.北京市：气象出版社，2007：296.

［27］Tarhule A，Woo M.Changes in rainfall characteristics in Northern Nigeria［J］.International Journal of Climatology.1998，18（11）：1261-1271.

［28］Pettitt A N.A Non-Parametric approach to the change-point problem［J］.Applied Statistics.1979：126-135.

［29］张顺谦，马振峰.1961-2009年四川极端强降水变化趋势与周期性分析［J］.自然资源学报，2011，26（11）：1918-1929.

［30］彭晓芬，黄甫则，周汝良.云南省年均降雨量空间插值模拟方法比较［J］.西南林学院学报，2010，30（5）：25-28.

［31］符传博，吴涧，丹利.近50年云南省雨日及降水量的气候变化［J］.高原气象，2011，30（4）：1027-1033.

Spatio-temporal Characteristics of Extreme Precipitation in Yunnan Province from 1958－2013

Yang Xiaojing，Xu Zongxue，Zuo Depeng and Liu Lin
（1．Key Laboratory ofWater and Sediment Sciences，Ministry of Education，College ofWater Sciences，Beijing Normal University，Beijing 100875，China；2．Joint Center for Global Change Studies，Beijing 100875，China）

Changes of extreme precipitation in Yunnan Province，southwestern China，are analyzed by using observed daily data from 28 meteorological stations during the period of 1958-2013.In order to detect possible trends，change points，periods and spatial distributions of the time series，analysiswere performed with Mann-Kendal trend test，moving t test，Mann-Kendall abrupt change analysis，Pettit test and inverse distance weighting.Results indicated that annual totalwet-day precipitation（PRCPTOT）displayed a downward tendency at the rate of-11.8mm／10a，consecutive wet days（CWD），number of heavy precipitation days（R10 and R20）also showed a decreasing trend，while the contribution of extreme precipitation to total precipitation exhibited a significant upward trend.Change points in consecutive dry days（CDD），R10，R20 and PRCPTOT，CWD，which can reflect the characteristics of average precipitation，were not detected.Change points in CWD，very wet days（R95p），extreme wet days（R99p），and simple daily intensity index（SDII）were detected in 2002，1993，1980 and 1994，respectively.These indices reflect the changes of extreme precipitation features sensitively and efficiently.All extreme precipitation indices had similar oscillation cycles except the CDD，R99p and SDII，which had three main characteristic timescales at28a，22a and 13a，and the corresponding cycle is 18 year，14 year，and 8 years，respectively.According the meteorological geographic zoning，the precipitation ranks from high to low in Yunnan Province was southwest，southeast，northwest，central，and northeast.Except CDD，CWD，SDII，and PRCPTOT，spatiotemporal distribution for other indiceswere consistentwith each other.Themaximum precipitation did not occur in central region；however extreme droughts and extreme precipitation risk in this region were higher than other areas.At the same time，the spatial distribution characteristics of extreme precipitation in other areas are comparatively similar with average annual precipitation.Overall，the extreme precipitation occurred more frequently，and extreme precipitation occurred more intensively since 2002.Further studies for the future should focus on extreme precipitation in Yunnan Province.

extreme precipitation indices；tendency；period；abruption；spatial distribution；Yunnan

X43；P42

A

1000-811X（2015）04-0178-09

10.3969／j.issn.1000-811X.2015.04.032

杨晓静，徐宗学，左德鹏，等.云南省1958-2013年极端降水时空变化特征分析［J］.灾害学，2015，30（4）：178-186.［Yang Xiaojing，Xu Zongxue，Zuo Depeng，etal.Spatiotemporal characteristics of extreme precipitation in Yunnan Province from 1958-2013［J］.Journal of Catastrophology，2015，30（4）：178-186.］*

2015-04-10 修回日期：2015-05-12

中国工程院重大咨询项目“我国旱涝事件集合应对战略研究”（2012-ZD-13）

杨晓静（1988-），女，云南昆明人，博士研究生，主要从事水文学及水资源方面研究.E-mail：yxj＠mail.bnu.edu.cn

徐宗学（1962-），男，山东淄博人，教授，博士生导师，主要从事水文学及水资源研究.E-mail：zxxu＠bnu.edu.cn