果蝇优化算法在边坡最小安全系数搜索中的应用*

贺子光，赵法锁，2，武 斌，汪班桥，段 钊

（1.长安大学地质工程与测绘学院，陕西西安710054；2.西部地质资源与地质工程教育部重点实验室，陕西西安710054；3.西安科技大学地质与环境学院，陕西西安710054）

果蝇优化算法在边坡最小安全系数搜索中的应用*

贺子光1，赵法锁1，2，武 斌1，汪班桥1，段 钊3

（1.长安大学地质工程与测绘学院，陕西西安710054；2.西部地质资源与地质工程教育部重点实验室，陕西西安710054；3.西安科技大学地质与环境学院，陕西西安710054）

提出将果蝇优化算法结合简化Bishop法对边坡最小安全系数进行搜索，针对基本果蝇优化算法局部寻优精度不高且易陷入局部最优的缺点，提出将果蝇优化算法和具有很强局部搜索能力的单纯型法相结合，并借鉴遗传算法中的杂交操作，以克服基本果蝇算法存在的不足。算例计算结果表明：果蝇优化算法是一种简洁、高效的边坡最小安全系数搜索方法，改进后的果蝇优化算法具有更高的收敛精度和可靠性，为边坡最危险滑动面搜索和最小安全系数的计算提供了一种新的全局求解策略。

边坡；果蝇优化算法；单纯型法；杂交操作；最小安全系数

极限平衡法是当前国内外应用最为广泛的边坡稳定性分析方法。它是传统边坡稳定分析方法的代表。而稳定性分析方法最终归结为一个求解目标函数（安全系数或加载系数）的极值问题，即求解相应最小安全系数所对应的临界滑动面。对于均质土坡，安全系数可采用解析法计算；而对于非均质土坡，由于土体参数的不同和土层的复杂性，其安全系数所对应的目标函数通常为多维、多极值的，传统优化方法不能很好地解决该问题。近年来肖专文［1］、何则干［2］、李守巨［3］、邹广电等［4］分别利用遗传算法、遗传模拟退火算法、非线性规划等搜索算法来研究边坡的稳定性，均取得了较好的效果。但遗传算法在搜索时，存在早熟收敛、计算量大等缺陷；非线性规划在求解目标函数呈高度非线性且为非凸优化问题时，容易陷入局部最优。因此，寻求一种有效、准确的方法进行边坡最小安全系数搜索是一个亟待解决的问题。

果蝇优化算法［5-6］（Fruit Fly Optimization Algorithm，FOA）是由台湾学者潘文超在2011年6月提出的种群全局优化进化算法。该算法容易理解，编码简单且易于实现；此外，果蝇优化算法的调节参数少，全局搜索能力强，收敛速度快，具有很强的鲁棒性和适应性，在多个领域已得到应用；但该算法也存在一些不足之处，其局部搜索能力不强，导致后期搜索效率降低，且容易陷入局部最优解。为此，本文将果蝇优化算法和具有很强局部搜索能力的单纯型法相结合，并借鉴遗传算法中的杂交概念，提高种群多样性，从而能够较为准确地获取全局最优解。

1 边坡最小安全系数搜索的优化模型

简化Bishop法是目前常用的一种刚体极限平衡方法，其不仅假定滑动面是个圆弧，还假定条间力的方向为水平方向，较其他简化方法更为方便、准确。简化Bishop法滑体与条块示意图见图1。滑动面对应的安全系数公式：

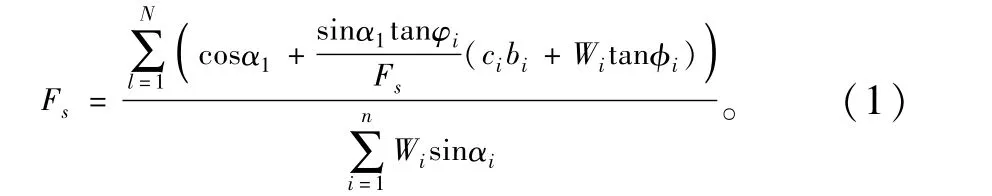
式中：N为条分数；Fs为对应滑动面的安全系数；αi为第i条土条滑动面法向与竖向的夹角；ci、φi分别为滑动面所在土层的粘聚力和内摩擦角；bi为第i条土条的宽度；Wi为第i条土条的重力。

式（1）为一隐式表达式，安全系数需通过迭代求解。当边坡的几何参数和力学参数给定时，安全系数是圆弧的圆心坐标和圆弧半径的函数，即：

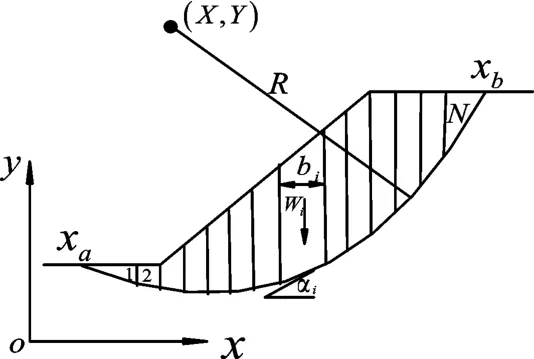
图1 简化Bishop法滑体与条块示意图

式中：x0、y0和R分别为滑动面圆弧的圆心坐标和圆弧半径。式（2）则转化为一个优化问题：

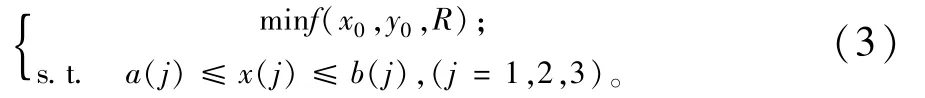
式中：X＝｛x（j），x（1）＝x0，x（2）＝y0，x（3）＝R｝为优化变量，［a（j），b（j）］为第i个变量的取值区间。

2 基于混合果蝇优化算法搜索边坡最小安全系数

2.1 基本果蝇优化算法

果蝇优化算法是一种基于果蝇觅食行为推演出的寻求全局优化的新方法。果蝇可以嗅到空气中的各种气味，甚至能嗅到40 km以外的食物。根据气味方向，飞近食物位置，然后通过敏锐的视觉发现食物与同伴的位置，并且飞向该方向。

依据果蝇搜索食物的特性，将果蝇优化算法归纳为以下几个必要的步骤［7－8］。

步骤1：设定种群规模Sizepop，最大迭代数Maxgen，随机初始化果蝇群体位置X＿axis和Y＿axis。

步骤2：赋予果蝇个体利用嗅觉搜寻食物之随机方向与距离，RandomValue为搜索距离。

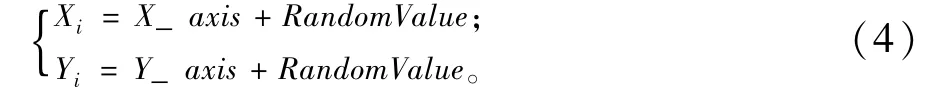
步骤3：由于无法得知食物位置，因此先估计与原点之距离Disti，再计算味道浓度判定值Si，此值为距离之倒数。

步骤4：将味道浓度判定值Si代入味道浓度判定函数（或称为适应度函数Fitness function），用来求出果蝇个体位置的味道浓度Smell（i）。

步骤5：找出该果蝇群体中味道浓度最佳的果蝇个体（最小化问题）。

步骤6：记录并保留最佳味道浓度值bestSmell与其X，Y坐标，这时候果蝇群体利用视觉向该位置飞去。

步骤7：进入迭代寻优，重复执行步骤（2）～步骤（6），并判断最佳味道浓度是否优于前一迭代最佳味道浓度，并且当前迭代次数小于最大迭代次数Maxgen，若是则执行步骤（6）。

2.2 混合果蝇优化算法

尽管FOA具有很多其他算法不具有的优点，但是该算法存在局部搜索能力不强且容易陷入局部最优解，而导致后期收敛精度不高的缺点。针对该问题，本文将单纯型法和基本果蝇优化算法相结合［9］，同时引入遗传算法中的杂交操作，形成混合果蝇优化算法（Mixed Fruit Fly Optimization Algorithm，MFOA）。新算法采用进化停滞步数t作为执行条件，当t≥T（进化停滞步数阈值）时，以当前最优个体位置给单纯型法进行初始化，利用单纯形法在最优个体位置的邻域范围内重新搜索，直到满足终止条件为止；然后以单纯型法搜索到的最优解为基础，首先将最优解复制N个，对该N个个体按一定杂交概率将一定数量的个体放入杂交池内，池中个体随机两两杂交，进而形成新的果蝇个体，对新果蝇个体进行二次寻优［10］，从而使算法能够获取较为准确的最优解。具体实施步骤如下所示。

步骤1：初始化参数，群体规模Sizepop，最大迭代数Maxgen，随机初始化果蝇群体位置X＿axis和Y＿axis，进化停滞代数阈值T，最优果蝇个体复制个数N，杂交概率Pc，杂交池比例大小Sp。

步骤2：采用式（1）随机产生果蝇群体。

步骤3：采用式（2）～式（4）对果蝇个体进行操作。

步骤4：记录并保留最佳味道浓度值bestSmell、最优果蝇个体位置X＿axusb、Y＿axisb和停滞步数t。

步骤5：当t≥T时，缩小解空间，用单纯形法搜索。以最优果蝇个体为当前最优解，在当前最优解的基础上，利用式（10）缩小解空间。

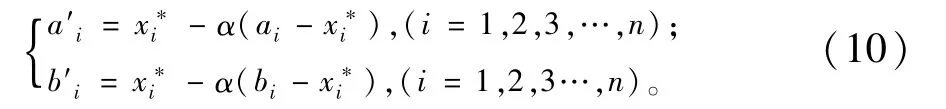
式中：0≤α≤1，根据多次试验，α通常取0.618。值得注意的是，上式中的与最优果蝇位置到原点的距离相对应，即

根据最优果蝇个体位置给单纯形法进行初始化，利用单纯型法在新的解空间搜索，直到满足终止条件为止。

步骤6：当r＜Pc（r为分布于［0 1］的随机数）时，首先按照式（11）复制N个最优果蝇个体X＿axisbj，Y＿axisbj（j＝1，2，3，…，N）。

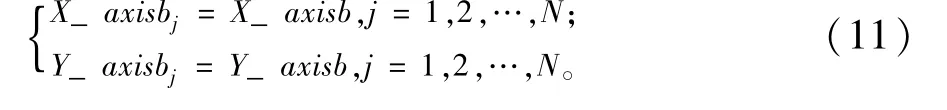
步骤7：执行杂交操作。根据杂交概率选取指定数量的个体放入杂交池内（杂交池比例大小为Sp），池中个体两两随机杂交，产生同样数目的新个体，新个体X坐标和Y坐标的计算公式见式（12）和式（13）。

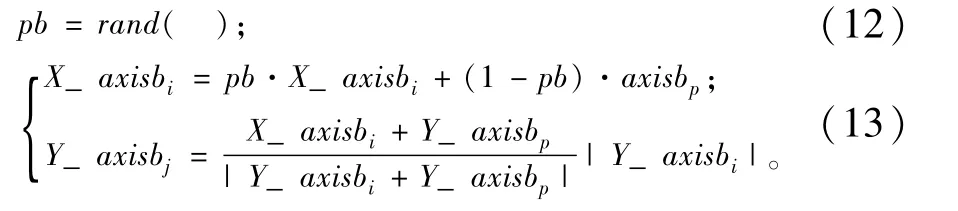
式中：j＝1，2，…Sp·N。

步骤8：按照式（14）先估计新位置X＿axisb′j、Y＿axisb′j与到原点之距离Dist′j，再按照式（15）计算新位置味道浓度判定值S′j（1，2，…，N）。

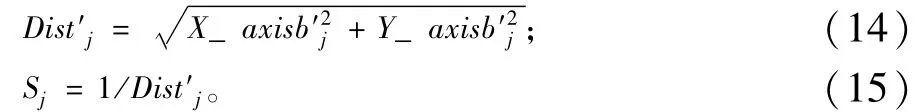
步骤9：将味道浓度判定值S′j代入味道浓度判定函数，求出新位置的味道浓度Smell′j（j＝1，2，3，…，N）。

步骤10：若Smell′j＜Smellbest，则Smellbest＝Smell′j，X＿axisb ＝ X＿axisb′j，X＿axisb ＝X＿axisb′j（j＝1，2，…，N）。

步骤11：进入迭代寻优，重复执行步骤（2）～步骤（10），直至当前迭代次数等于最大迭代数Maxgen。

流程图如图2所示。

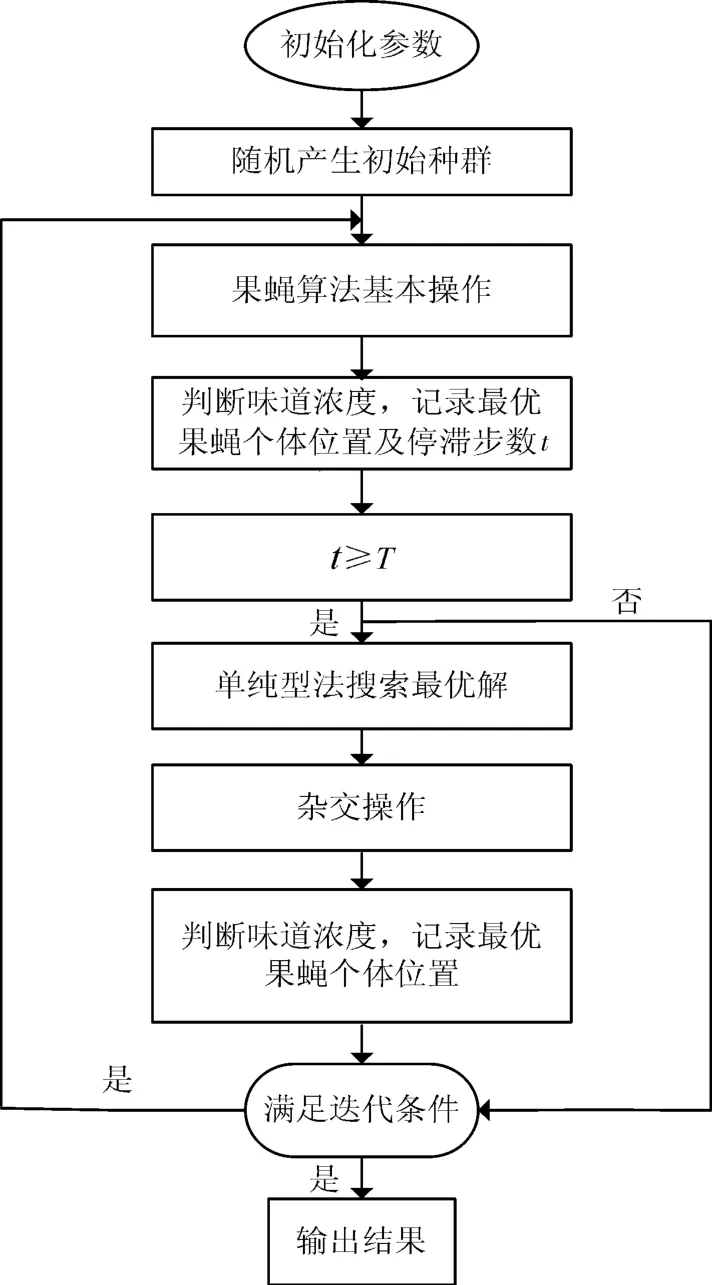
图2 果蝇算法优化流程图

3 工程算例分析

根据本文给出的混合果蝇优化算法的具体实施步骤，结合简化Bishop法，编写了相应的边坡最小安全系数搜索程序。需要指出的是，由于果蝇优化算法目前只能计算变量为正值的情况，鉴于此，在利用混合果蝇优化算法搜索最危险滑面时，应该对边坡采用相对坐标或者整体使边坡位于坐标系的第二象限，确保各变量取值为正值。为验证本文方法在边坡稳定分析中的有效性，对两个经典边坡进行最危险滑动面搜索。

3.1 算例1

为了验证本文方法的可行性和准确性，本文对两个经典算例进行了分析。算例1为一非均质土坡，材料特性见表1，边坡形状如图3所示。

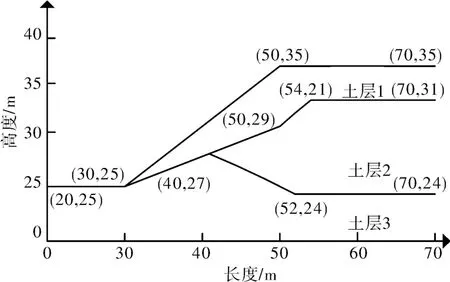
图3 算例1边坡剖面

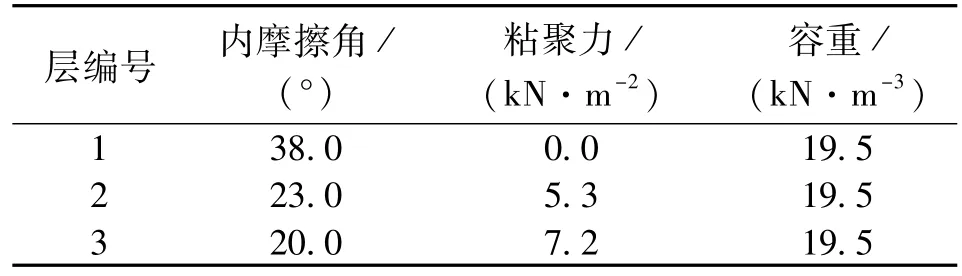
表1 土层计算参数

这里分别采用FOA方法和混合FOA进行计算，算法的公共参数设置为：群体规模40，迭代步数1 000，最优果蝇个体复制数N取20，杂交率Pc取0.7，杂交池比例大小Sp取0.4，进化停滞步数阈值为5，结果见表2。通过对比分析，两者搜索到最优解与ACADS给出的安全系数裁判解值非常接近，说明该方法可行。

表2 不同方法的结果对比

改进后的果蝇优化算法控制参数的不同选取，直接对算法的性能产生较大影响，控制参数主要包括杂交率Pc和杂交池比例大小Sp。下面讨论各控制参数对最小安全系数搜索的影响规律。由于算法具有一定的随机性，为了减小随机性导致的计算结果误差，在同样的参数情况下，程序均运行10次，以平均值作为衡量依据。

（1）杂交率Pc对最小安全系数的影响

图4中给出了算例1在不同杂交率时，最小安全系数的收敛情况。其中种群规模为40，最优果蝇个体复制数N＝20，杂交池比例大小Sp＝0.4。

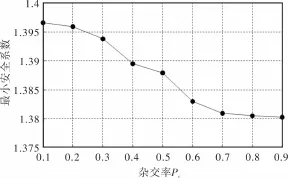
图4 杂交率对最小安全系数的影响

从图4可以看出，当杂交率Pc逐渐增大时，最小安全系数有逐渐变小的趋势。当Pc＝0.7，0.8，0.9时，最小安全系数相差很小。但Pc＝0.7时算法的运行时间较Pc＝0.8，0.9时的运行时间少。综合考虑精度和运行时间，Pc＝0.7为最宜选择。

（2）杂交池大小比例Sp对最小安全系数的影响

图5中给出了算例1在不同杂交池比例大小时，最小安全系数的收敛情况。其中种群规模为40，最优果蝇个体复制数N＝20，杂交率Pc＝0.7。

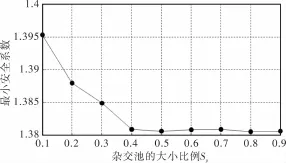
图5 杂交池的大小比例对最小安全系数的影响

由图5可以看出，最小安全系数随杂交池比例的增大而不断减小。当Sp＝0.4～0.9时，所对应的最小安全系数相差很小。当Sp＝0.6，0.7，安全系数略有增加，这是由算法的随机性引起的，因为Sp的不同取值所对应的最小安全系数相差很小，使随机性对计算结果的影响相对增大。但从整体变化趋势分析，最小安全系数随着杂交池比例的增大而减小。一般情况下，杂交池比例大小Sp取0.4。在算例2中杂交率Pc取0.7，Sp取0.4。

3.2 算例2

为进一步说明本文方法的优越性，下面对一个更为复杂的海堤边坡计算分析，边坡剖面如图6所示，材料特性见表3。

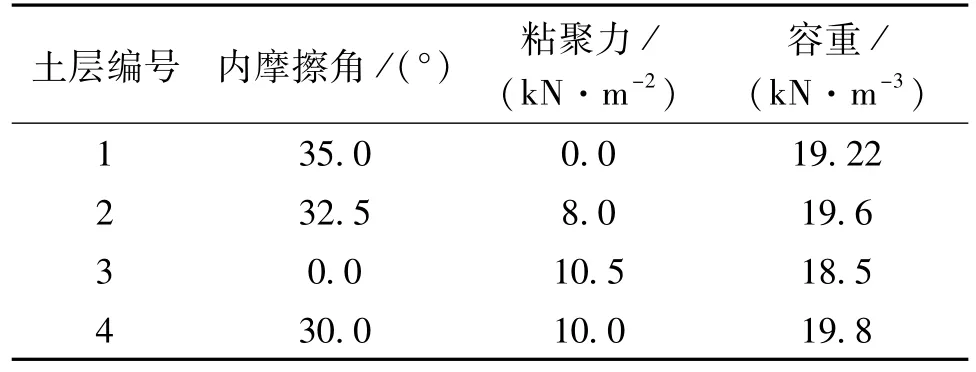
表3 土层计算参数

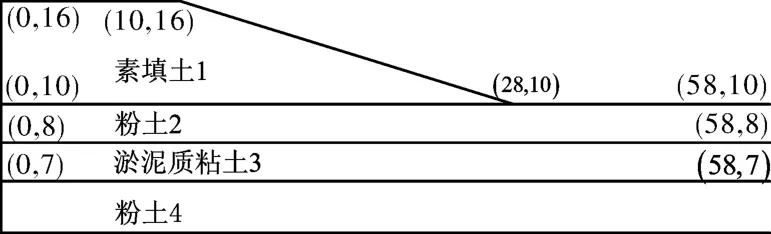
图6 复杂海堤边坡及地基剖面

本算例中，为了考察本文算法在不同搜索空间中的全局搜索能力，将在5个不同的搜索空间中进行计算。土条数取50，算法的公共参数设置如下：群体规模40，迭代步数2 000，最优果蝇个体复制数N＝20，杂交率Pc＝0.7，杂交池比例大小Sp＝0.4，进化停滞步数阀值T＝5。与其他方法的计算结果的对比见表4。

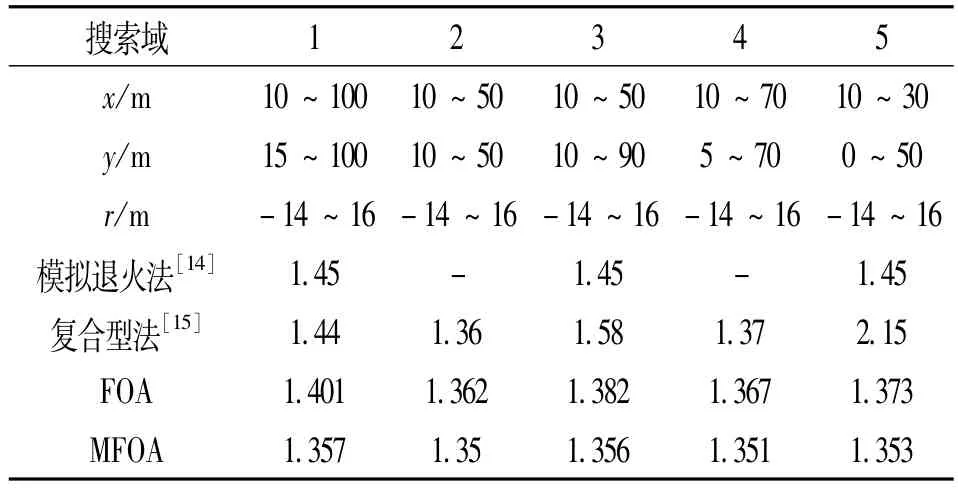
表4 复杂海堤边坡安全系数计算结果

由表4可以看出，本文方法的搜索结果较模拟退火方法和复合型法更优，且方法在不同搜索域内的搜索结果均具有更好的效果。在计算域2内，分别采用FOA和MFOA进行计算，为验证本文方法的稳定性，减小算法由于随机性而产生的误差，两种方法均运行10次，对其结果进行统计分析，结果见表5。10次计算结果中，最小安全系数Kmin＝1.35，若｜si－1.35｜／1.35≤ξ，则称第i次寻优成功。si为算法第i次搜索到的最优值，ξ为给定的阈值。定义寻优成功率η＝寻优成功的次数／总寻优次数。表5中给出ξ＝0.02时，FOA和MFOA的寻优成功率。图7为在计算域2中，FOA和MFOA各自最小安全系数的收敛过程。

表5 FOA和MFOA的计算结果统计分析

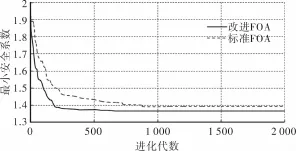
图7 最小安全系数优化进程图

由表5和图7可知，改进后的果蝇优化算法的最优解优于基本果蝇优化算法的最优解，且改进后的果蝇优化算法的收敛速度更快。从标准差和寻优成功率两个指标可以看出：改进后的果蝇优化算法的收敛可靠性更加稳定，表明其局部搜索能力和全局搜索能力均得到提高。

4 结论

（1）本文将果蝇优化算法与简化Bishop法相结合，用于边坡最危险滑动面搜索。算例1所示的计算结果说明该方法可准确、有效地搜索到边坡最危险滑动面及相应的安全系数。

（2）针对果蝇优化算法局部寻优精度不高和易陷入局部最优的缺点，提出了将单纯型法和果蝇优化算法相结合，并引入遗传算法中的杂交操作，形成了混合果蝇优化算法。

（3）算例2计算结果分析表明：改进后的果蝇优化算法较基本果蝇优化算法的局部搜索能力和全局搜索能力均得到了提高。

［1］ 肖专文，张奇志，顾兆岑，等.边坡最小安全系数的遗传算法［J］.沈阳建筑工程学院学报，1996，12（2）：144-147.

［2］ 李守巨，刘迎曦，何翔，等.基于模拟退火算法的边坡最小安全系数全局搜索方法［J］.岩石力学与工程学报，2003，22（2）：236-240.

［3］ 邹广电.边坡稳定分析条分法的一个全局优化算法［J］.岩土工程学报，2002，24（3）：309-312.

［4］ 何则干，陈胜宏.遗传模拟退火算法在边坡稳定分析中的应用［J］.岩土力学，2004，25（2）：316-319.

［5］ PANWen-tsao.A new fruit fly optimization algorithm：Taking the financial distressmodel asan example［J］.Knowledge-based Systems，2012，26：69-74.

［6］ 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估［J］.太原理工大学学报：社会科学版，2011，29（4）：1-5.

［7］ 韩俊英，刘成忠，王联国.动态双子群协同进化果蝇优化算法［J］.模式识别与人工智，2013，26（11）：1057-1067.

［8］ 韩俊英，刘成忠.自适应变异的果蝇优化算法［J］.计算机应用研究，2013，30（9）：2641-2644.

［9］ 肖云华，陈剑平，张丽.基于单纯型-混沌优化算法的边坡稳定性分析［J］.自然灾害学报，2012，21（1）：174-178.

［10］谭乐祖，任东彦，温巧林.基于杂交粒子群算法的弹炮混编防空群火力优化模型［J］.兵工自动化，2010，29（2）：16-19.

［11］吕文杰，李晓军，朱合华.基于遗传算法的边坡稳定分析通用算法［J］.岩土工程学报，2005，27（5）：595-599.

［12］Baker R.Determination of the critical slip surface in slope stability computations［J］.International Journal of Numerical and Analysis Methods in Geomechnics，1980，4（4）：333-359.

［13］康飞，李俊杰，马振岳.基于人工蜂群算法的边坡最危险滑动面搜索［J］.计算机应用研究，2013，30（9）：2641-2644.

［14］李亮，迟世春，林皋.引入退火机制的复合形法在边坡最小安全系数搜索中的应用［J］.水利学报，2005，36（1）：83-88.

［15］李亮，迟世春，林皋.基于蚁群算法的复合形法及其在边坡稳定分析中的应用［J］.岩土工程学报，2004，26（5）：691-696.

The Application of FOA in Searching for M inimum Safety Factor of Slope

He Ziguang1，Zhao Fasuo1，2，Wu Bin1，Wang Banqiao1and Duan Zhao3
（1．College of Geology Engineering and Geomatics，Chang′an University，Xi′an 710054，China；2．Key Laboratory ofWestern China Mineral Resources and Geological Engineering，Ministry of Education，Xi′an 710054，China；3．College of Geology and Environment，Xi′an University of Science and Technique，Xi′an 710054，China）

A new method combining fruit fly optimization algorithm with simplified Bishop Method is presented to search minimum safety factor of slope.In order to overcome the shortcoming of easily relapsing into local optimal solution and low convergence precision，we propose combining the fruit fly optimization algorithm with simplex algorithm，and introduce the hybridization operation in genetic algorithms to form a mixed fruit fly optimization algorithm.Results of practical examples show that the fruit fly optimization algorithm is a simple and efficientmethod for searchingminimum safety factor，and improved mixed method has higher convergence accuracy and reliability. Thus，a concise effective global strategy is provided for searching the critical slip surface and calculating theminimum factor of safety in slope stability.

slope；fruit fly optimization algorithm；simplex algorithm；hybridization operation；minimum safety factor

TU323；X43

A

1000-811X（2015）04-0029-05

10.3969／j.issn.1000-811X.2015.04.006

贺子光，赵法锁，武斌，等.果蝇优化算法在边坡最小安全系数搜索中的应用［J］.灾害学，2015，30（4）：29-33.［He Ziguang，Zhao Fasuo，Wu Bin，et al.The Application of FOA in Searching for Minimum Safety Factor of Slope［J］.Journal of Catastrophology，2015，30（4）：29-33.］

2015-04-27

2015-06-15

国家自然科学基金应急管理项目（41440021）；陕西省科技计划项目（s2012sF3082）；西安科技大学博士启动基金项目（2014QDJ029）

贺子光（1987-），男，河南焦作人，博士研究生，主要从事边坡工程稳定性方面的分析和研究.

E-mail：hzg198762＠163.com